Abstract:

Key words: Contagion, evolutionary epidemiology of culture, cultural evolution, cultural selection, meme, allomeme, cultural trait, genetic algorithm, globalisation.

1. Introduction

A large literature exists on the relationship between genetic isolation and cultural isolation (e.g. Sokal et al. 1989;Barbujani & Sokal 1990; Vona et al. 1996; De Silvestri & Guglielmino 2000; Gonzalez Jose et al. 2002). Genetic isolation may be the result of a 'founder effect', where a population expands rapidly from a small set of original progenitors. This often happens in colonial situations, e.g. in South Africa (Torrington & Viljoen 1991), Venezuela (Ramirez-Duque et al. 1982; Vivenes De Lugo et al. 2003), Canada (Scriver 2001) or Finland (Kittles et al. 1999). It may also follow a sudden 'population crash' caused by a natural disaster or epidemic disease, followed by regeneration of the population from the survivors (Ambrose 1998; Harpending et al. 1998). All of these factors may also cause cultural isolation, which can then contribute to further genetic isolation if interbreeding with geographically neighbouring populations is prevented or reduced by cultural factors. However, the two phenomena are not necessarily related, and one may exist without the other.

Cultural isolation may be seen as an extreme case of 'memetic isolation' (Gatherer 2002b), defined here as the situation in which any cultural trait of a society is different to the corresponding mutually exclusive cultural trait, the 'allomeme' (Durham 1991), of any of its surrounding cultures. A true cultural isolate will be memetically isolated for an extensive selection of cultural traits.

In classic mathematical memetic theory, 'vertical transmission' refers to traits that are passed on from one generation to the next, specifically from parents to progeny (a variant is 'oblique transmission' in which traits are passed within families, but not necessarily from parent to child). By contrast 'horizontal transmission' refers to transmission within a single generation, either between siblings or other genetic relatives, or within a non-related peer group (Cavalli-Sforza & Feldman 1981). One of the results of this body of theory is that traits with more than one means of transmission have a greater tendency to homogeneity within populations, and also that horizontally transmitted traits are more likely to be spatially clustered (Cavalli-Sforza & Feldman 1973, Uyenoyamaet al.. 1979, reviewed by Cavalli-Sforza 1979). 'Spatial clustering' in this context means that individuals exhibiting the trait tend to be found in closer geographical proximity than those who do not exhibit the trait.

The present paper further investigates this area of theory using agent-based simulation. The simulation was previously described in detail in Gatherer (2002b), and may be considered as a variant of the Social Interaction Model (SIM) simulation of Axelrod (1997). Two questions are asked:

1) Under what combination of parameters is memetic isolation maximised?

2) Under what combination of parameters is memetic isolation minimised?

The answers provided enable us to refine the predictions of the original theoretical treatments of transmission and its relation to spatial clustering of traits (reviewed by Cavalli-Sforza 1979).

2. The Model

Figure 1: Rules for possibility of interaction in Axelrod's SIM. Cultural traits are represented by letters, and coloured to show which are found in common between pairs. Since the upper pair has 4 out of 6 cultural traits in common, these two societies can interact. However, the lower pair only has 2 traits in common and therefore cannot interact.

Once the two societies have established an interaction, one society may randomly adopt a cultural trait from the other. This is illustrated in Figure 2. At the end of the interaction, one of the societies has become slightly more similar to its neighbour. It is easy to see how this simple situation mirrors the process of cultural transfer in real societies. Cultures with very differing languages, religions or habits may fail to make the necessary cultural contact. However, once a certain threshold has been crossed and communication is established, cultural interaction can commence. This model makes the assumption that there is no selection for or against any cultural trait, or that traits are imposed wholesale, e.g. by conquest.

Figure 2: Adoption of one cultural trait from adjacent society in interacting SIM pair. Trait X in the right society is replaced by trait V from the left society. Having had 4 traits in common, the pair of societies now has 5 in common.

This process is repeated over several cultural generations in a grid of several cultures, typically 10 by 10, starting from a random distribution of traits. One of the principal results of SIM is that cultural 'blocs' are formed, i.e. areas on the cultural landscape with several near-identical cultures. This is especially the case if the probability of interaction is varied according to the relatedness of a pair of societies, i.e. if a pair of societies with 5 traits in common has more chance of interaction that a pair with only 3 in common, and so on. Intuitively, it can be seen that his tends to mean that societies that have previously interacted will be increasingly likely to interact further in future generations, thus producing a positive feedback.

The variation on SIM presented previously by Gatherer (2002b) uses an identical concept of a grid of societies in geographical space. The size of grid presented in the scenarios below is 10 x 10, the same order of magnitude used by Axelrod (1997). However, the focus is switched to the individual agent with the society rather than the society as a whole. SIM assumes that each society is culturally homogeneous, insofar as each society has a single set of cultural traits. Figure 3 shows how this may be adapted to allow individuals within societies to differ in their repertoire of memes and genes. The word 'genes' in this case is used as a shorthand for 'strictly vertically transmitted memes', since in haploid organisms (i.e. those with a single copy of each gene in their genomes) these categories are formally equivalent (Cavalli-Sforza & Feldman 1981). In panel A of Figure 3, a grid of nine societies may be seen. Individuals are indicated as circles with their vertical memetic component as the letter A or B, and their horizontal memetic component as the colour red or blue. These individuals may perform three kinds of lifecycle activity: reproduction, migration and cultural interaction. In Figure 3A and 3C, cultural interaction is indicated with a black arrow if it occurs within societies (e.g. in the bottom right society of panel A, an individual with blue meme teaches it to an individual with red meme, thus resulting in that individual having blue meme in panel B), and a green arrow if it occurs across inter-societal boundaries. Reproduction is indicated with a white arrow and the newly produced individuals are surrounded by a dotted line in 3A and 3C. Migration is indicated by a blue arrow, and can only occur to neighbouring societies (in other words this is a 'two-dimensional stepping stone' model of migration - Rychkov & Sheremetyeva 1977). Panels 3B and 3D illustrate the end result after the processes displayed in 3A and 3C. The societies in panels A and B are coloured blue or orange according to the majority of blue or red memes respectively. In panels C and D the societies are coloured yellow or grey according to the majority of genes (or strictly vertical memes) A and B, respectively.

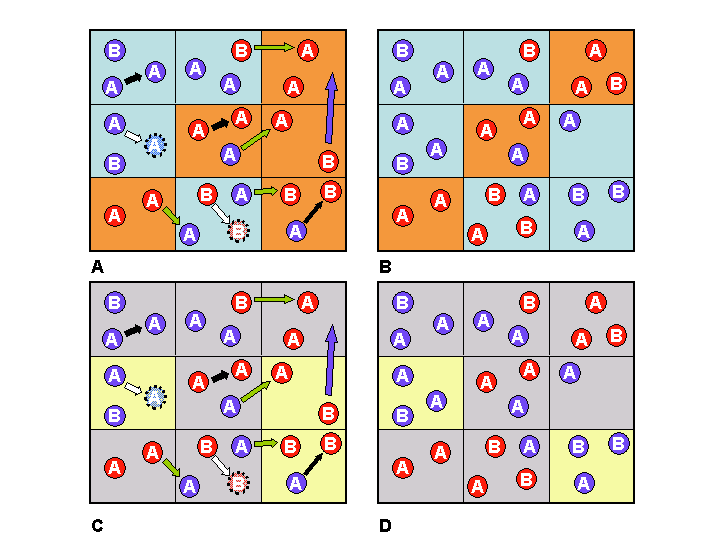
Figure 3: Reproduced from Gatherer (2002b). A and B labels are strictly vertical memes, red and blue colours are horizontal memes. Thus a blue individual labelled B has the B vertical meme and the blue horizontal meme. Black arrows: horizontal cultural interaction within societies. Green arrows: horizontal cultural interaction between societies. Blue arrows: migration of individuals. White arrows: reproduction (new progeny are identical to their parents and are shown with dotted outlines). Orange squares: societies with majority red memes. Light blue squares: societies with majority blue memes. Grey squares: societies with majority of A vertical memes/genes. Yellow squares: societies with majority of B vertical memes/genes. Fuller explanation given in text.

In summary, the simulation consists of a grid of connected societies populated by cultural agents, its dynamics being defined with a set of four simple parameters:

• the rate of population growth, r
• the rate at which teaching/learning occurs, o
• the rate at which teaching/learning occurs between societies, n
• the rate at which individuals migrate to neighbouring societies, m

INITIALIZATION:
For each of the 100 cells in the 10-by-10 array:
{
	place two Agents in each cell
	randomly assign one of four Gene attributes to each individual
	randomly assign one of four Meme attributes to each individual
}
ITERATION:
For 100 generations do the following:
{
	For each Agent:
	{
		If Agent Meme attribute = "A" and CultSel = "Y"
			{
			Double parameters n and o for that agent
			}
		If Agent Meme attribute = "A" and NatSel = "Y"
			{
			Double parameter r for that agent
			}
		If a random number x < r
			{
			Reproduce Agent
			}
		If a different random number y < o
			{
			If same random number y is also < n
				{
			Transmit Meme to any Agent in any adjacent cell
				}
			else
				{
				Transmit Meme to any Agent in same cell
				}
			}
		If a different random number z < m
			{
			Migrate Agent to adjacent cell
			}
	}
}
END.

Additionally, 'cultural selection' or 'natural selection' may be applied to one of the memes in the population. Here, these terms are used in the sense of Cavalli-Sforza & Feldman (1981), as follows: a culturally selected meme is one that has an increased probability of transmission relative to its allomemes; a naturally selected meme is one that provides a survival or reproductive advantage to those individuals that exhibit that behaviour or cultural trait.

Figure 4 provides a diagrammatic representation of the agent in UML (Universal Modelling Language). The simplicity of this agent (all attributes and methods public, no constructors etc) is due to its implementation as a Perl record rather than a true object in Java or C++. Perl records are fairly analogous to struct in C. Agents have one of four Meme attributes ("A", "B", "C", "D") and one of four Gene attributes ("1", "2", "3", "4").

Figure 4: UML diagram for the Agent class. Attributes are above the line and Methods below. Public scope is represented by a "+" (all are public)

Perl scripts are provided in the Appendix that:

• run the simulation with graphical output
• implement a genetic algorithm (GA) to optimise the parameters.

Both scripts require Perl, and the first also requires the Tk graphics library. A recent version of ActivePerl (Build 6 series or more recent, freely available from http://www.activestate.com) provides all the necessary library components. All scripts provided have been tested on RedHat Linux 6 running Gnome, and on Microsoft Windows 98.

3. The Effects of Varying Parameters on Memetic Isolation

The 'memetic state' of a society for a certain cultural trait, is here defined by the 'first-past-the-post' voting method. The Meme attributes of each agent in the society are scored, and if allomeme "A" scores more than any of the other three Meme attributes, the memetic state of that society is "A". If allomeme "A" is not the highest scoring attribute, the memetic state of that society is "not-A". 'Memetic isolation' occurs when that society's 'memetic state' is "A" and that of all its immediate neighbours is "not-A". The overall memetic isolation is the percentage of societies that are in this state. It is admitted that 'first-past-the-post' is potentially a flawed means of scoring a society, but it is often used in sociological contexts. For instance, statements such as the "Belgium is a Catholic country" are simply expressions of such head counts. Qualifying those situations where the 'first-past-the-post' voting produced a narrow majority, perhaps by the use of a 'marginal' label, could further refine the model. However, this would be complex enough to merit another paper, and so is not dealt with here.

'Genetic isolation' can similarly be calculated using the Gene attribute "1". Since the agents are haploid (i.e. they have only a single Gene attribute), the Gene is equivalent in terms of its transmission to a strictly vertically transmitted meme, as demonstrated by Cavalli-Sforza & Feldman (1973). It is thus possible to contrast 'memetic isolation' and 'genetic isolation' in terms of the likelihood of isolation for horizontal and vertical memes. Therefore, 'genetic isolation' is used hereafter simply as a shorthand for 'memetic isolation for strictly vertical traits'.

3.1 Scenario 1: The Random Background - the "strictly vertical model"

The scenario is initialised with two individuals per cell, and allowed to run for 100 generations with a rate of population growth (r) of 0.01 per generation. Migration (m), and the two social interaction variables (o and n) are set at zero. This simulates a situation where societies grow slowly in size, but there is no 'horizontal transmission' (Cavalli-Sforza & Feldman 1981), or movement of individuals across society boundaries. It is essentially a non-cultural population, or perhaps more exactly a population where culture is contained strictly within vertical lineages. This is given merely to demonstrate the properties of the system in a background state, where as little as possible is happening except the effects of randomness over a large number of cycles. It is difficult to think of a real-world example of this kind of cultural situation; even non-human species with aspects of culture, such as song birds and great apes, do not limit cultural transmission within genetic lineages (e.g. Burnell 1998;Lynch et al. 1989; Reader & Laland 2000; van Schaik et al. 2003). The scenario was repeated 100 times and the average memetic and genetic isolation measured. These were found to be 3.23% and 3.00% respectively. Statistical significance was assessed using a paired t-test. In this and all subsequent scenarios, t-tests are two-tailed, as there is no a priori expectation that parameters will increase or decrease levels of isolation. A paired t-test between the genetic and memetic isolation values for each of the 100 runs, was not significant, thus indicating that both horizontal and vertical memes behave identically in strictly vertical populations. In effect, the 'horizontal memes' are forced to become vertical memes by the absence of cultural interaction in the population, and thus this scenario constitutes a sort of reductio ad absurdum. However, it is necessary to demonstrate the basic background behaviour against which other scenarios will be measured.

3.2 Scenario 2: Introducing Cultural Exchange Within Societies - the "desert island model".

Social interaction within societies is now permitted, by raising parameter o to 0.5. This means that each agent will transmit a horizontal meme with probability 0.5 within its lifetime, in other words half of all agents transmit horizontally per generation, and half do not. All other parameters are the same. This recreates the situation of societies between which there is no contact, but which have a flourishing social life of their own, such as might occur on extremely isolated oceanic islands. It should be noted at this point, and for all subsequent scenarios, that it is recognised that real societies are infinitely more complex than any simulation can reproduce. The purpose of adding labels such as 'desert island' to the simulations, is really to serve as a mnemonic shorthand, and also to perhaps act as an 'intuition pump' for practical applications.

After 100 generations, over 100 runs of the scenario, the average genetic and memetic isolation values are 3.16% and 4.08% respectively. A paired t-test shows these to be statistically significantly different at p<0.0004. Thus, against a background of no migration and no cultural exchange between societies, social interaction within our artificial societies increases the likelihood that those societies will be memetic isolates. This is because the rate of the random walk amongst competing allomemes in those societies is speeded (see Gatherer 2002a, Fig. 2). If o is raised to 1, allowing each agent a successful cultural transmission event per lifetime, the figures are essentially unchanged. This is called a 'desert island' model, since it would apply only to societies that were completely cut off from the rest of the outside world. Some examples are known, of which the best studied is perhaps that of the Bounty mutineers on Pitcairn Island, who remained completely undiscovered for decades after settling, and in effective cultural isolation for some years after. In this period they were able to evolve a unique culture incorporating both European and Polynesian elements, including a new creole English language (Refshauge & Walsh 1981). If one imagines a thought experiment in which the Bounty mutineers colonised two separate islands, mutually unconnected, the model predicts that they would become memetic isolates for many traits. This rarely applies to many island archipelagos, as the inhabitants are often in contact, albeit infrequently. This leads to the next scenario where such an arrangement is permitted.

3.3 Scenario 3: Introducing Limited Cultural Exchange Between Societies - the "Palaeolithic model".

Parameter n is now raised from zero to 0.01. This permits cultural exchange with a neighbouring society at a probability of 0.01 x o per individual per generation. Therefore at o of 0.5, the rate of inter-cultural exchange is 0.005. The societies are now no longer totally isolated "desert islands", but have the kind of casual contact perhaps normal for sparsely distributed and occasionally trading nomadic bands. Over 100 runs of the scenario, again for the standard 100 generations, average genetic isolation remains around the background level at 3.12%, but memetic isolation drops to 1.78%. A paired t-test shows this to be a significantly different value for memetic isolation at levels of p tending to zero. Thus even a small amount of cultural exchange between our artificial societies may, ceteris paribus, create tendencies to cultural homogenisation on a local geographical scale. Cultural blocs (Axelrod 1997) thus begin to emerge out of a patchwork background. Where parameter n is increased, memetic isolation falls even further: at n = 0.1, memetic isolation falls to 0.71%. Thus in a scenario of 100 societies, most runs terminate without a single memetic isolate at the end of 100 generations. This is called the 'Palaeolithic model' as it very roughly recreates a situation hypothesised to have existed in Late Ice Age Europe, where nomadic bands of hunters of large herds of bison, mammoths etc, would have existed in isolation punctuated by brief seasonal periods of contact at assembly points, perhaps associated with exchange of gifts, arrangement of marriages and ritual behaviour (e.g. Rudgley 2000). A more modern example may be provided by the Andamanese, who remained in relative isolation within their archipelago for many thousands of years (e.g. Thangaraj et al. 2003). Again it bears reemphasis that the correspondence between the artificial societies and the anthropological examples given is quite naïve, and really just raises the issue of how better models of such societies could be created, rather than claiming to have created one here.

3.4 Scenario 4: Introducing Natural Selection - the "Neolithic model".

Meme "A" is now submitted to natural selection. This means that those agents with Meme attribute "A" have twice the normal chance of reproduction of those with the other three allomemes. Meme "A" agents thus reproduce above replacement at a probability of 0.02 per generation, instead of the 0.01 for the other three allomemes. This is termed here the "Neolithic Model" as it is reminiscent of one of the main theories for the Neolithic transition in Europe, namely that the cultural activity of farming provided a reproductive and survival advantage, in that early farmers were able to feed more children and live longer to reproduce more, compared to their Mesolithic hunter-gatherer neighbours (Renfrew 1987). If m, n and o are all set to zero, so that there is no migration or cultural exchange within the population, but natural selection is permitted to increase r from 0.01 to 0.02 for Meme "A" individuals, genetic isolation after 100 generations is 3.68% and 2.34%. This memetic isolation is significantly different to the background "pre-cultural model" (See 3.1), although both models have no cultural exchange. The reason for this is that the evolutionary advantage of Meme "A" in terms of natural selection means that this meme will tend to take over the populations in which it is found. If it happens to occur in two adjacent societies, even at initial low frequencies, it will eventually run to fixation in those societies. Of course, this is not really a good "Neolithic model", as Neolithic societies also had cultural exchange as well as natural selection for a meme (assuming for the present that this particular theory of Neolithic transition by demic expansion is true). A second "Neolithic model", allowing levels of cultural exchange equivalent to the "Palaeolithic model", i.e. o = 0.5 and n = 0.01, has levels of genetic and memetic isolation of 3.37% and 1.11%, respectively. A t-test shows that this is a significantly different level to that when there is no natural selection. Natural selection of a meme thus reduces its likelihood of memetic isolation.

3.5 Scenario 5: Introducing Cultural Selection - the "Contagion model".

The second "Neolithic model" above, now has natural selection of Meme "A" replaced by cultural selection. This means that Meme "A" will be transmitted at double the normal frequency of cultural exchange. Thus with o = 0.5 and n = 0.01, as above, Meme "A" has probabilities of transmission of oA = 1 and nA = 0.02 . Genetic and memetic isolation after 100 generations average to 3.24% and 0.21%, respectively. Therefore, cultural selection almost removes memetic isolation entirely.

3.6 Summary of scenarios

Table 1 show the summary of the scenarios

Table 1: Summary of the average genetic and memetic isolations resulting from the various scenarios. The 'strictly vertical' model provides the random background level of isolation. The 'desert island model' shows the highest level of memetic isolation. m: migration, n: cultural interaction within societies, o: cultural interaction between societies

Several questions may now be answered by using t-tests to compare the statistical significance of differences between rows in Table 1. In this section, t-tests are two-tailed and non-paired, since comparison is between different scenarios. An F-test is first carried out to establish if the t-test should be heteroscedastic or homoscedastic.

What factors affect genetic isolation?: Method: t-tests between genetic isolation data for all rows against row 3.1 (where there is the random background level of genetic isolation). Answer: no model significantly changes the likely degree of genetic isolation of each society. The differences within the range of 3.12% to 3.68% are all explicable as statistical random variation. This applies equally to cultural traits that are strictly vertically transmitted.

What factors affect memetic isolation?: Method: t-tests between memetic isolation data for all rows against row 3.1 (where there is the random background level of memetic isolation). Answer: by contrast with the above, all models have a level of memetic isolation significantly different to the random background at p<0.01. The answer is therefore completely different to the above, in that one might say that several factors may influence memetic isolation, including cultural and natural selection, and the rates of cultural transmission.

Does the "Neolithic - 2" have less memetic isolation than the basic "Neolithic" model? Method: t-tests between memetic isolation data for rows "3.4 Neolithic" and "3.4 Neolithic - 2". Answer: yes, at p tending to zero. Therefore, it is possible to conclude that an increase in social interaction within a society decreases memetic isolation when the meme is under natural selection, whereas it increases it when natural selection is not operating (compare "Strictly vertical" and "Desert Island").

Does "Contagion" have less memetic isolation than any of the other models? Method: t-tests between memetic isolation data for all rows against row 3.5. Answer: yes, "Contagion" has a significantly lower level of memetic isolation than all other models at p tending to zero. It is thus possible to say that culturally selected traits are unlikely to exist in isolation.

4. The Genetic Algorithm

The above set of simulations only dealt with seven scenarios as compared to a random background. However, since there is a combinatorial explosion of possible scenarios, a heuristic method must be used to select the scenario most likely to give rise to extreme conditions.

A standard method for use in such situations is the Genetic Algorithm (GA - reviewed by Bentley 1999). The general form of the GA used here is as follows:

START: Randomise representations of the parameters in a linear string.
FOR n CYCLES
{
	Assess the result of those parameters by 100-generation simulation
	Rank strings by the result under investigation (e.g. maximal memetic isolation)
	Discard very worst performers
	Recombine and/or mutate remainder of unacceptable perfumers
	Retain and reproduce acceptable performers to maintain constant numbers of strings
}
END.

In the GA presented here, the threshold below which GA strings are discarded is 0.775 standard deviations below or above the average memetic isolation, depending on whether the GA is attempting to maximise or minimise memetic isolation. The threshold for mutation and/or recombination is 0.5 standard deviations above/below the average. Mutation and recombination occur with probabilities of 0.05 and 0.1 respectively, but only within the sub-standard group. The better performing strings are thus protected from mutation and recombination (this is quite a Lamarckian GA!). These properties were derived by a process of empirical trial and error, and there are many other forms of GA that could be used. The balance between homogenisation, due to selection, and diversity, due to mutation and recombination, is a delicate one, and has to be solved afresh for every situation in which a GA is used. It should be noted that the fitness landscape is extremely noisy. In all the scenarios above in section 3, the standard deviation of the memetic isolation is high. For this reason, it appears to be more profitable to protect the better performing strings. The GA process is illustrated in diagrammatic form in Figure 5, and the continuing high standard deviation may be seen in Figure 6.

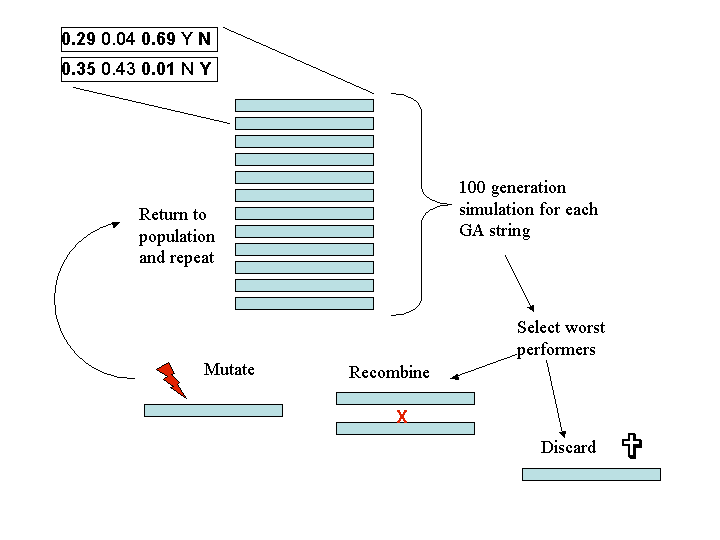
Figure 5: Diagrammatic representation of the GA process. The starting sets of parameters for the model are represented as a string of length 5. Each string is run as a separate simulation, and the results are assessed according to the desired outcome (e.g. high memetic isolation or low memetic isolation). The 'worst' performers according to the desired criteria are either discarded, mutated or recombined with a randomly chosen other member of the population. The discarded strings are replaced by randomly chosen strings from the better performing part of the population. Selection of GA strings thus tends to homogenise the population while mutation and recombination maintain some variability. The whole process was repeated over 100 cycles.

A set of GA strings was prepared by semi-randomly initialising the variables, m, n and o, and the selective conditions for cultural and natural selection, 50 times. The initialisation is semi-random as the starting set was biased to give fairly low levels of migration. The initial set produced is shown in abbreviated form in Table 2. After 100 iterations of a GA process, selecting for maximum memetic isolation at each stage, the 50 populations corresponding to the 50 GA strings have average memetic isolation of 4.60% and average genetic isolation of 4.72%. The set after 100 GA generations is shown in abbreviated form in Table 3. The most obvious feature of the action of the GA over 100 generations of searching for best parameters for maximum memetic isolation, is to eliminate cultural and natural selection. The GA also optimises memetic isolation by reducing the rate of cultural exchange within the culture, variable o, from the initial average of 0.462 to less than 0.005. Migration is increased from 0.048 at initialisation to 0.559. The optimal value for teaching to other societies is also maintained fairly high, at 0.432 from 0.501 at initialisation, but this will still represent a small level of cultural exchange since the background probability of cultural exchange is less than 0.005.

Table 2: Truncated listing of 50 GA strings semi-randomly initialised at 5 parameters.

Table 3: Truncated listing of 50 GA strings after 100 generations of the GA process, selecting for maximum memetic isolation.

When the same process is performed, but the selective conditions are to minimise memetic isolation, the resulting average parameters are compared in Figure 4. The minimisation GA was only performed over 7 rounds of selection, as compared to 100 rounds for maximization, as it rapidly achieves a near-zero rate of memetic isolation.

The progress of the memetic isolation-maximising GA is shown in Figure 6.

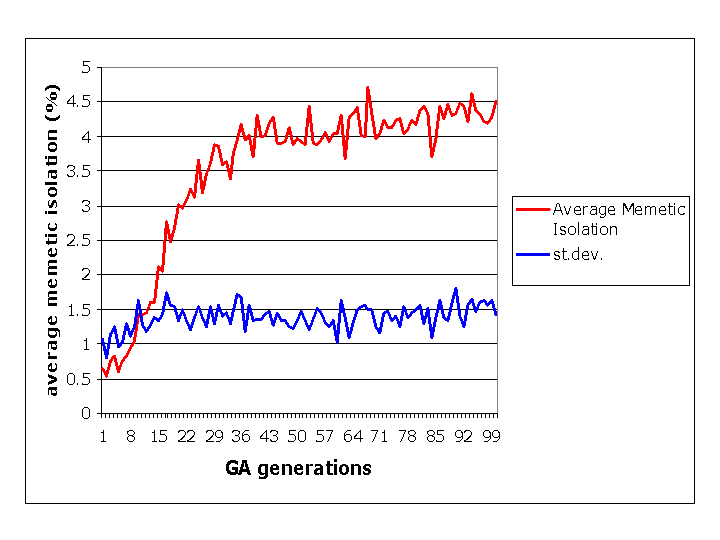
Figure 6: Progress of the genetic algorithm in selecting parameters to maximise memetic isolation. Red: the average memetic isolation in the 50 populations corresponding to the 50 GA strings. Blue: the standard deviation of that average throughout the 50 populations. The persistence of a relatively high standard deviation illustrates the 'noisiness' of the system.

5. Discussion

The contemporary phenomenon of globalisation involves cultural as well as economic aspects. It has been estimated that 5.6% of the world's languages are in danger of extinction, and a further 4.4% have recently become extinct (Sutherland 2003). In the Social Interaction Model (Axelrod 1997), this phenomenon was seen as an emergent property. SIM is another grid-based agent model in which neighbouring agents are permitted to exchange information with other societies providing they shared at least one cultural trait. SIM has a single agent per grid square, which can either be taken as an individual or as a whole, and necessarily homogeneous, society (Axelrod suggests 'homogeneous villages'). There is no migration. SIM leads to the increasing homogenisation of agents in close proximity, while at the same time agents that had by chance no common traits with their neighbours, remain completely differentiated. If the SIM agents are treated as individuals, SIM demonstrates how neighbouring individuals can form homogeneous cultural areas. Similarly, if the SIM agents are regarded as homogeneous societies, SIM demonstrates the formation of cultural 'blocs' on a local geographical basis. The model presented here differs from SIM, in that it is necessarily based on individuals. Societies are simply geographical areas, whose cultural profiles depend on those of the agents that inhabit them. Another important difference is that in the present model, the level of social interaction between societies is constant for each run of the scenario, and is defined by parameter n. However, in SIM, the analogous parameter is proportional to the number of cultural traits that neighbouring agents have in common. Thus, if there are no traits in common, neighbouring agents will not interact, thus creating a local 'desert island' model. If the SIM agents are seen as homogeneous societies, SIM thus simultaneously operates a 'desert island' model and a 'Palaeolithic model' within the same scenario, with the two models operating in different parts of the grid, with shifting boundaries as the scenario progresses. A model more similar to the present one in its structure, is given by Ray et al. (2003), but those authors focus exclusively on the genetic phenomena and do not deal with horizontally transmitted cultural entities.

The genetic algorithm process presented here seeks to derive parameters for the prevention of cultural blocs. It delivers maximal memetic isolation (an average of 4.6% of societies are memetic isolates after 100 generations of the scenario) at levels of social interaction tending to zero (less than 0.5% per person per lifetime), and with high migration (over 55% per person per lifetime), where no selective conditions operate. This describes a rather nightmarish scenario where there is little or no social communication between continually wandering individuals. There is some superficial similarity here to theories of 'alienation' (Geyer 1994). Although technically, this might be the optimal way of maintaining memetic diversity in a grid of artificial societies, it is clearly not a solution that any would prescribe in the real world. It is also completely vulnerable to selection pressures where they arise. Even in situations of very low social interaction, a culturally selected meme will tend to spread through a population (see Gatherer 2002a, Fig. 4). When there is no social interaction at all, and cultural selection ceases to operate, natural selection can still push memes to fixation through growth of the lineages that exhibit them. In effect, extreme migration rates cause the cellular nature of the scenario to break down, and effectively become a single society. Parameters o and n then cease to have any significance, as cultural transfer occurs principally by transfer of people.

How would one make the model more comparable to the real world? Empirical studies of Australian Aborigines suggest a realistic figure of 0.12 to 0.13 for m, where the pattern of migration is mostly to neighbouring tribal groups and rarely to more distant tribes, reflected in the present model (Lasker & Crews 1996). Migration rates of m ~ 0.55 are rare in the real world. Where they do occur they are often in specific directions, e.g. invasions, flight of refugees, economic migration, and are not reproducible in the present model. Even when they do, they are often smaller than m ~ 0.55. For instance even at the height of the potato famine in Ireland, the total decline in population over the decade 1841-1851 was about 20%, including migration and death (although of course a decade does not constitute a lifetime, so the figures are not strictly comparable). The largest migration occurring in a single year, the 17 million people that migrated from one part of the Indian subcontinent to another after partition, still only accounted for some 7% of the Indian population at the time. Modern radiochemistry is beginning to show that Neolithic populations may have been more mobile than previously thought (e.g. Montgomery et al. 2000). There are some interesting questions that could be addressed in this area using scenarios of the sort presented here, once accurate parameters can be estimated from the empirical data, such as why late Neolithic Malta became a cultural isolate after two millennia in contact with the rest of the Mediterranean (e.g. Robb 2001; Schulting & Richards 2002). Empirical studies to determine realistic values of parameter o may be more problematic, but there may be some clues from anthropological field studies of cultural transmission (e.g. Hewlett & Cavalli-Sforza 1986).

When set to minimise memetic isolation, the GA simply identifies cultural selection as the over-riding factor in this. As modelled here, contagious memes run to fixation within societies, and when transferred to neighbouring societies, do the same there. However, it is also clear that this is a naïve representation of the likely course of contagion within a society. Gatherer (2002a) shows that there are several factors that can derail 'the contagionist paradigm', and that random, or pseudo-random, walks are more likely than sigmoid curves when considering meme frequencies within any society.

The effect of modern mass communication media is to amplify the horizontal mode of transmission so that one individual can communicate with many more individuals simultaneously than would be possible in a lifetime of individual contacts (Cavalli-Sforza & Feldman 1981). This situation is not explicit modelled either here, or in SIM, but could easily be incorporated. Axelrod (1997) suggests a model where long-range interactions are permitted and probabilities of interaction are based on such long-range communication networks, rather than geography. Gould & Tornqvist (1971) describe a transition from a spatially contagious pattern of cultural spread to a hierarchical one dominated by rapid transfers between urban centres. These authors cite Pyle's (1969) work on cholera by way of example: the 1832 epidemic in Montreal and New York spread slowly down the Ohio/Great Lakes river system. In 1865 by contrast, several major cities, by that time connected by rail, were struck simultaneously, and the second wave of the epidemic struck towns connected to those major cities. Thus, for societies in the industrial phase of development, it is clear that such a spatial grid model (whether using SIM or the model presented here) is inadequate.

However, although the initial model was conceived as a representation of a geographical grid of societies, in order to compare the results of simulations with a geographically ordered ethnographic data set (Gatherer 2002b), it is also possible to consider it more abstractly, as a single large society partitioned into smaller social networks. This effect is in any case forced on the scenario at high values of m, such as that produced by the GA. The arrangement of the cells on the grid does not then refer to any geographical separation of sub-societies, but to their separation in terms of the likelihood of weak ties. Sub-societies that are not adjacent on the grid will have no weak ties at all between them, and those that are adjacent will have weak ties with probability n per individual per generation.

In summary, it has been known for over a quarter of a century that memes have a greater tendency to homogeneity within populations than genes, and also that memes are more likely to be spatially clustered (reviewed by Cavalli-Sforza 1979). In the context of the present scenario, 'spatial clustering' can be taken to mean an absence of memetic isolation, or in Axelrod's terms the formation of 'cultural blocs'. The scenarios presented here demonstrate that, where societies are totally isolated (the "desert island" model, section 3.2) the tendency to memetic isolation is actually increased. However, where cultural exchange, even at a tiny level, is permitted between neighbouring societies, memetic isolation declines precipitately (the "Palaeolithic" model, section 3.3). Where the meme is also under selection, especially cultural selection, memetic isolation falls towards zero (the "Neolithic" and "Contagion" models, sections 3.4 and 3.5). Therefore the inherent tendency of memes to be more spatially clustered than genes depends on the existence of cultural bridges, or 'weak ties' (Granovetter 1973), between societies. The GA results confirms the primacy of selective pressures in creating spatial homogeneity, but also suggests that such homogeneity can be rapidly fractured by high migration rates. Memetic systems can be seen to be highly unstable, especially when the selective forces at work within them are also cultural. Culture is always close to chaos.

Appendix:  Code Listings

All listings require Perl to be installed, and should run under both windows and Unix.  In the event of any problems, please contact the author.

The code for the graphical simulator:

• As a perl file: sim.pl
• As a text file: sim.pl.txt

• As a perl file: ga.pl
• As a text file: ga.pl.txt
  

References

Ambrose SH (1998) Late Pleistocene human population bottlenecks, volcanic winter, and differentiation of modern humans. Journal of Human Evolution 34, 623-651.

Axelrod R (1997) The dissemination of culture: a model with local convergence and global polarization. Journal of Conflict Resolution 41, 203-226.

Barbujani G & Sokal RR (1990) Zones of sharp genetic change in Europe are also linguistic boundaries. Proceedings of the National Academy of Sciences, USA 87,1816-1819.

Bentley P (1999) (ed.). Evolutionary Design by Computers. Morgan Kaufmann, San Francisco.

Burnell K (1998) Cultural variation in savannah sparrow, Passerculus sandwichensis, songs: an analysis using the meme concept. Animal Behaviour 56, 995-1003.

Cavalli-Sforza LL & Feldman MW (1973) Models for cultural inheritance. I. Group mean and within group variation.. Theoretical Population Biology 4, 42-55.

Cavalli-Sforza LL & Feldman MW (1981) Cultural Transmission and Evolution. Princeton University Press, Princeton.

Cavalli-Sforza LL (1979) Cultural change and its relevance for human genetics. Ciba Foundation Symposium 66, 5-23.

De Silvestri A & Guglielmino CR (2000) Ethnicity and malaria affect surname distribution in Consenza Province (Italy). Human Biology 72, 573-583.

Durham WH (1991) Coevolution: Genes, Culture and Human Diversity. Stanford University Press, Stanford.

Gatherer D (2002a) The Spread of Irrational Behaviours by Contagion: An Agent Micro-Simulation. Journal of Memetics - Evolutionary Models of Information Transmission 6. http://cfpm.org/jom-emit/2002/vol6/gatherer_d.html

Gatherer D (2002b) Identifying Cases of Social Contagion Using Memetic Isolation: Comparison of the Dynamics of a Multisociety Simulation with an Ethnographic Data Set. Journal of Artificial Societies and Social Simulation 5(4). http://jasss.soc.surrey.ac.uk/5/4/5.html

Geyer F (1994) Alienation, Participation and Increasing Societal Complexity. Kybernetes 23, 1-3

Gonzalez Jose R, Garcia-Moro C, Dahinten S & Hernandez M (2002) Origin of Fueguian-Patagonians: an approach to population history and structure using R matrix and matrix permutation methods. American Journal of Human Biology 14, 308-320.

Gould P & Tornqvist G (1971) Information, Innovation and acceptance. In: Hagerstrand T & Kuklinski A (eds.) Information Systems for Regional Development, Lund Series in Geography, Ser. B, Human Geography 37, 149-168.

Granovetter M (1973) The strength of weak ties. American Journal of Sociology 78, 1360-1380.

Harpending HC, & al. (1998) Genetic traces of ancient demography. Proceedings of the National Academy of Sciences, USA, 95, 1961-1967.

Hewlett BS & Cavalli-Sforza LL (1986) Cultural transmission among Aka pygmies. American Anthropologist 88, 922-934.

Kittles RA, & al. (1999) Autosomal, mitochondrial, and Y chromosome DNA variation in Finland: evidence for a male-specific bottleneck. American Journal of Physical Anthropology 108, 381-399.

Lasker GW & Crews DE. (1996) Behavioral influences on the evolution of human genetic diversity. Molecular Phylogenetics and Evolution 5, 232-240.

Lynch A, Plunkett GM, Raker A & Jenkins P (1989) A model of cultural evolution of chaffinch song derived with the meme concept. The American Naturalist 133, 634-653.

Montgomery J, Budd P & Evans J (2000) Reconstructing the lifetime movements of ancient people: a Neolithic case study from southern England. European Journal of Archaeology 3, 370-386.

Pyle G (1969) Diffusion of cholera in the United States. Geographical Analysis 1, 59-74.

Ramirez-Duque P, Arends T & Merino F (1982) Chediak-Higashi syndrome: description of a cluster in a Venezuelan-Andean isolated region. Journal of Medicine 13, 431-451.

Ray N, Currat M & Excoffier L (2003) Intra-Deme Molecular Diversity in Spatially Expanding Populations. Molecular Biology and Evolution 20, 76-86.

Reader SM & Laland KN (2000) Diffusion of foraging innovations in the guppy. Animal Behaviour 60, 175-180.

Refshauge WF & Walsh RJ (1981) Pitcairn Island: fertility and population growth, 1790-1856. Annals of Human Biology 8, 303-312.

Renfrew C (1987) Archaeology & Language: The Puzzle of the Indo-European Origins. Jonathan Cape, London.

Robb J (2001) Island identities: ritual, travel and the creation of difference in Neolithic Malta. European Journal of Archaeology 4, 175-202.

Rudgley R (2000) Secrets of the Stone Age: A Prehistoric Journey. Century, London.

Rychkov YG & Sheremetyeva VA (1977) The genetic process in the system of ancient human isolates in North Asia. In: Harrison GA (ed.), Population Structure and Human Variation, Cambridge University Press, Cambridge, 47-108.

Schulting RJ & Richards MP (2002) The wet, the wild and the domesticated: the Mesolithic-Neolithic transition on the west coast of Scotland. European Journal of Archaeology 5, 147-189.

Scriver CR (2001) Human genetics: lessons from Quebec populations. Annual Review of Genomics and Human Genetics 2, 69-101.

Sokal RR, Oden NL, Legendre P, Fortin MJ, Kim JY & Vaudor A (1989) Genetic differences among language families in Europe. American Journal of Physical Anthropology 79, 489-502.

Sutherland WJ (2003) Parallel extinction risk and global distribution of languages and species. Nature 423, 276-279.

Thangaraj K, & al. (2003) Genetic Affinities of the Andaman Islanders, a Vanishing Human Population. Current Biology 13, 86-93.

Torrington M & Viljoen DL (1991) Founder effect in 20 Afrikaner kindreds with pseudoxanthoma elasticum. South African Medical Journal 79, 7-11.

Uyenoyama M, Feldman MW & Cavalli-Sforza LL (1979) Evolutionary effects of contagious and familial transmission. Proceedings of the National Academy of Sciences, USA 76, 420-424.

Van Schaik CP, & al. (2003) Orangutan cultures and the evolution of material culture. Science 299, 102-105.

Vivenes De Lugo M, Rodriguez-Larralde A & Castro De Guerra D. (2003) Beta-globin gene cluster haplotypes as evidence of African gene flow to the northeastern coast of Venezuela. American Journal of Human Biology 15, 29-37.

Vona G, & al. (1996) Genetics, geography, and culture: the population of S. Pietro Island (Sardinia, Italy). American Journal of Physical Anthropology 100, 461-471.