Journal of Memetics - Evolutionary Models of Information Transmission, 6.
http://cfpm.org/jom-emit/2002/vol6/gatherer_d.html
A micro-simulation is described, for rational and irrational strategies in human mating behaviour. The spread of irrational behaviour through a population from a single initial individual, the `contagionist paradigm', is shown to be highly unlikely in most realistic circumstances. An exception to this rule is shown to be where the `self-fulfilling prophecy' phenomenon is exhibited, i.e.. the irrational meme affects the outcome of the mating. Additionally, where the irrational strategy, under conditions of self-fulfilling prophecy, is allowed to co-exist with a rational strategy (i.e.. a strategy based on factual information), both can proceed to fixation, resulting in a population of individuals exhibiting both rational and irrational memes simultaneously. However, where successful pairs are removed from the population, there is a tendency for neither behaviour to persist. Maintenance of either behaviour in the population under circumstances of removal of successful pairs requires a cultural information system, i.e.. one where a common pool of information may be accessed without a requirement for contagion. This implies that contagionist explanations of culture may be strictly limited in their application. Some attempt is then made to generalise the conclusions to financial systems.
This paper investigates an agent population exhibiting two kinds of behaviour:
These two kinds of behaviour are replicated in 2 ways:
The system simulated is that of human mate pairing. It is clear from biological studies that many species are very selective in mate choice, and that there may also be vigorous competition between individuals for mates. As Darwin (1872) recognised, these two factors have resulted in the phenomenon of sexual selection for a wide variety of traits in species ranging from insects to mammals. In some species, mate choice behaviour also has a cultural dimension which may amplify, or conflict with, any underlying innate biological tendencies (Wade & Pruett-Jones 1990; Laland 1994; Freeberg et al 1999). The simulation presented here attempts to dissect how a `rational' mating behaviour, arbitrarily taken to be selection of a mate of same status as oneself, conflicts with an `irrational' mating behaviour, for instance the use of astrology to select a mate. Note that such `astrological' behaviour need not necessarily always be maladaptive, since a good mate may coincidentally be chosen. It is, however, always `irrational' regardless of its adaptiveness. Although astrology is apparently believed by 25% of US adults (Blackmore 1999, p184), it may not necessarily figure very prominently in real human partner choice (but perhaps in other aspects of reproduction, see Goodkind 1993). However, the example is given merely to contrast irrational and rational memes in a simple contagion-based agent-pair interaction system. Generally similar dynamics may occur wherever agents are exchanging information repeatedly in a closed system. Additionally, it should be pointed out that the mated pairs are not engaged in reproduction, or even necessarily in any physical copulation, but rather in partner choice for potential reproduction. In other words, this model takes place within a single generation. Moreover, no genetic components are envisaged, and the behaviours are taken to be totally cultural. Finally, the population is not spatial segmented, and any individual can potentially mate with any other of the opposite sex. Ways in which the model could be expanded to incorporate a combination of genetics, multiple generations, and spatial heterogeneity are considered in the discussion.
Gender, status and `star sign' (attributes 1 -3) are considered fixed for any individual and cannot be changed. The behavioural states (attributes 4 and 5) relating to status and astrology may be changed under certain circumstances, representing a behavioural change in that agent. A `yes' state for astrology means that the individual will seek to ascertain the star sign of the other individual. Likewise a `yes' state for status results in behaviour to determine the status of the potential partner. The status-`yes' state is `rational' in that status objectively influences the likelihood of success of the pairing (in the simulation, whether or not is does so in real life is quite another matter - see Brown et al 1988; Pizzari 2001). By contrast, the astrology-`yes' state is `irrational' in that star sign has no objective effect on success (see Goodkind 1993, for an empirical example of how astrology may influence human reproductive behaviour).
Agents seek a mate at random from among the opposite sex in the population (as in Ophir 1998). The outcome of the mating (successful or unsuccessful) is determined by a combination of random chance, a background a priori likelihood of success, and various rules dependent on the types of agent involved. Having mated every individual in the population, the cycle repeats. Each iteration, the proportions of the population exhibiting the enquiry behaviours, i.e.. the `yes' states, for status (rational) and star sign (irrational) are recorded. In some later simulations, successfully mated pairs are withdrawn from the mating pool and replaced with naïve individuals, as would be the case if mated pairs were to concentrate on reproduction and cease to look for further partners
Each simulation is produced using Perl scripts which, along with the full list of rules used in the more advanced simulations, are available from http://www.geocities.com/derek_gatherer/supp.htm.
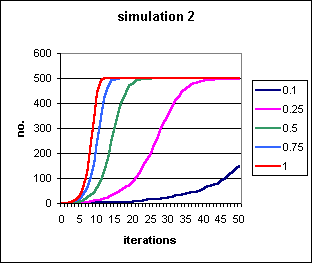
Figure 1: Spread of a contagious trait introduced by a single agent into a population of 500 agents, at differing values of probability of transmission per contact, p. Where p = 1, i.e.. the trait is always transmitted, it approximately doubles every iteration, and a population of 500 is almost always fixed by generation 12. These S-shaped curves represent the most trivial case of contagion, and are presented as a reference point for the curves in the subsequent simulations.
Although these curves are sometimes fairly flat, their shape is
still sigmoid, and the `contagionist paradigm' still applies. The only
variable is whether the contagion is slow or fast. For instance in Fig.1,
for p = 0.1, i.e. 10% chance of transmission per contact,
it still takes 45 iterations for 20% of the population to have been infected.
Thus, for cases of `biased transmission'/ `cultural selection', the contagiousness
of a trait is not important to the eventual outcome, ceteris paribus.
It is however, precisely this ceteris paribus assumption that is violated
in all but the most trivial cases.
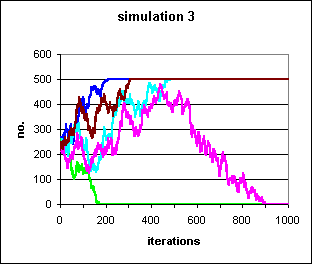
Figure 2: 5 runs of a simulation in which the likelihood of conversion to a trait and conversion away from a trait are equal in each contact. In a population of 500, each starting with 250 individuals exhibiting the trait, 3 populations become fixed for the trait (blue, brown and turquoise) and the trait becomes extinct in 2 (green and pink). These are the most trivial examples of random walks, and like the S-shaped curves in Figure 1 are given for the purposes of reference.
Random walks are totally random, by definition, but may appear directional.
Take for example the pink population in Fig. 2.
After a period of quasi-periodic movement upwards, it suddenly turns and
declines to zero. As this is an agent simulation, it is known that this
is simply a random walk. However, an empirical worker approaching evidence
in the other direction, might easily conclude, wrongly, that there must
be non-random influences on the trend. In a random walk, at p
= 0.5 as given here, any trajectory is equally likely and the odds of any
trajectory occurring are 0.5n (i.e.. pn)
for any particular trajectory of n steps. Since n
is 1000 in simulation 3, there are approximately
10301 different possible trajectories, all equally likely, and
each of which has an approximate probability of 10-301. Over
an infinite number of n, all trajectories will eventually
terminate in fixation or extinction, with equal probability (Kimura
& Ohta 1978, Kimura 1979).
The sensitivity of such a situation to variation in p may be illustrated by considering what happens when p deviates from 0.5. Effectively, even small deviations away from 0.5 will pull the random walk rapidly to fixation or extinction.

Figure 2b: 5 runs of a simulation in which the likelihood of conversion to a trait and conversion away from a trait are equal in each contact. Again a population of 500 is used, starting with 250 individuals exhibiting the trait. Varying values of p, the probability of conversion to the trait, are given.
The rapidity of fixation and extinction is almost too fast to see
over a timescale of 1000 iterations in Fig. 2b,
so the early stages of the 5 simulations are shown again in Fig.
2c. Where p <= 0.4 the trait barely survives 20 generations.
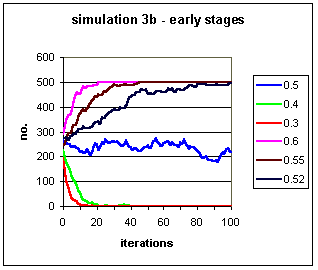
Figure 2c: The early stages of the simulations
given in Fig. 2b above.
In general, the probability of a random walk, where p is not equal to 0.5 are pn+(1-p)m, where n is the number of incremental turns and m is the number of decremental turns. Therefore where p is not equal to 0.5, not all walks are equally probable, and the walks are quasi-random. This much is trivial, once again, but illustrates how easily cultural traits may exhibit chaotic dynamics, especially if p is variable from generation to generation (dependent perhaps on other cultural factors). Under such circumstances, a predictive memetics would become virtually impossible, as cultural traits would swing wildly in frequency with apparently no rationale (perhaps a familiar scenario for empirical observers of culture). However, the situation does become more predictable as other factors are added to the simulation.
Let the outcome of pairings in each iteration be recorded. Let also the chance of success in each pairing be s (0 <= s <=1), the a priori success probability. A random number generator is used to generate a number between 0 and 1. If this random number is less than s, the pairing is deemed to have been successful. The following rules then apply:
Under such circumstances, it is again, as in simulation 3 above, virtually impossible for the irrational behaviour to colonise the population from a single individual. That is because the rules above are balanced, i.e.. the number of events causing a conversion in one direction is equal to the number of events causing conversion in the opposite direction (rules 1 & 3 versus 2 & 4).
As in the previous simulation, 5 populations are allowed to run for 1000 iterations with the initial frequency of the irrational behaviour at 50%. The chance of success for each pairing is also set at 50%.
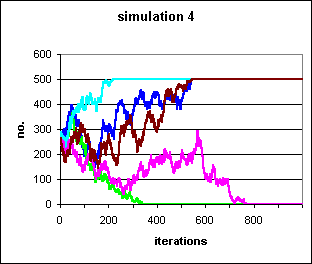
Figure 3: 5 populations of 500 individuals, with initially 250 individuals exhibiting the irrational behaviour, and the transmission of the behaviour dependent on the outcome of pairings. Although the dynamics of this simulation are strictly rule-based, and those of simulation 3 dependent on binomial chance, the population trajectories produced by the two systems are indistinguishable.
Bias is defined as the extent to which astrology will interfere with the potential success of a relationship on a scale of 0 to 1, where the pair have incongruent star signs, and one or both of the pair exhibit the astrology behaviour. This is programmed in the following manner. The a priori likelihood of success of a relationship is s, and bias is b, both are between zero and 1, and both are set in advance. A random number generator is again used to generate a number between zero and 1. Without bias, if that random number is less than s, the pairing is successful. With bias, b is subtracted from s. This reduces the likelihood that the random number will be less than s, and thereby `loads the dice' against success. Where the pair have congruent star signs, and one or both of the pair exhibit the astrology behaviour, bias acts in the other direction, to increase the chance of success. This is programmed by adding b to s, rather than subtracting it as above, and therefore increasing the likelihood of success. Where b-s is less than zero, the relationship is doomed to failure, regardless of the number produced by the random number generator. Likewise where b+s is greater than one, the relationship is guaranteed to succeed.
Where b = 0.5, populations run to fixation fairly smoothly for most values of s, provided the novel irrational meme can survive the first few iterations. This `self-fulfilling prophecy' thus changes the irrational behaviour from a randomly walking trait into a colonizing one. The `contagionist paradigm' of steady sigmoid curves, reappears.
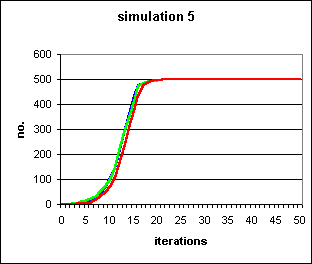
Figure 4: An irrational trait originating in a single individual, colonising a population of 500, running to fixation in under 25 generations in 3 separate runs (red, green and blue). 5 runs of this simulation were performed, of which the other 2 resulted in immediate extinction of the trait at the first iteration. This is clearly an S-shaped curve, demonstrating that, once the novel meme has survived the first few iterations, the `self-fulfilling prophecy' mechanism turns a random walk into an irresistible tendency. Parameters were s=0.5, b=0.3.
Status effects can co-exist with irrational bias effects. In the interaction of the 2 strategies, the following general rules apply. The full set of precise rules are available on http://www.geocities.com/derek_gatherer/supp.htm.
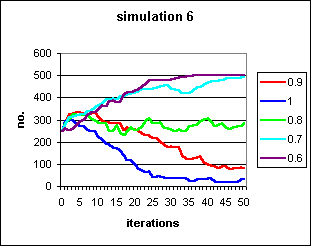
Figure 5: Progress to fixation or decline to extinction of rational behaviour under varying conditions of `self-fulfilling prophecy' bias, b, from 0.6 to 1, with an a priori likelihood of success of pairings of s = 0.5. In all runs, the irrational behaviour ran to fixation in 10 iterations.
This decreases the volatility of the system, and promotes the settling of the population settles into a stable state. The equilibrium position is determined by the relative values of s and b, and the speed with which it is obtained is dependent on the threshold for conversion, t.
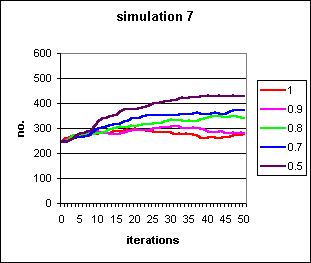
Figure 6: Progress of rational behaviour in the population under the same conditions as in figure 5 above (s constant at 0.5 and b run at 0.5 to 1), but with a threshold of 3 introduced. This delays fixation of rational behaviour under conditions of low bias, but also prevents its immediate extinction under conditions of high bias.
Where the a priori likelihood of success, s, is high, individuals are removed so rapidly from the population that neither the rational nor irrational behaviour is very persistent. Lowering s to 0.01, and with high self-fulfilling prophecy bias, b, it is possible to retain them for some longer time. However, the influx of new individuals wins out eventually.
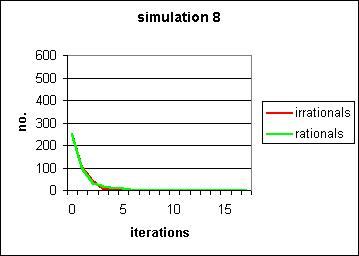
Figure 7: Replacement of successful pairs with naïve individuals rapidly removes both behaviours, rational and irrational, from the population. Compare with Figure 4. The same parameters are used, s = 0.5, b = 0.3, which would normally generate a powerful "self-fulfilling prophecy" for the fixation of irrational behaviour. However, here the arrival of waves of naïve agents overwhelms the capacity of the contagion system.
Thus rules 7 and 8 from simulation 6, above, are now altered to:
7. Based on success or failure, a contribution to the communal information pool is made. The agent states for the rational and irrational behaviours are still altered in the usual way if an agent is paired with an agent exhibiting the appropriate behaviour.Thus the communal information pool does not replace contagion, but supplements it. This simulates an element of `persuasion'. Agents still convert under the influence of other agents, both rationally and irrationally, if conditions are correct. However, where no persuasion is exercised, agents can still alter their behaviour if conditions are correct, and the cultural norm suggests they should. (Perhaps this violates Levy & Nail (1993)'s requirement for an absence of intentionality in a true contagion system, but I am unsure of what intentionality means in terms of software agents.)
8. But now additionally, behaviours can change even if an agent is not paired with an agent exhibiting the appropriate behaviour, subject to consulting the communal information pool for the latest consensus.
This helps to maintain steady random walks very near the starting values, after an initial movement upwards or downwards (dependent on starting parameters) as the contagion effect begins, before the communal information pool helps to correct it.
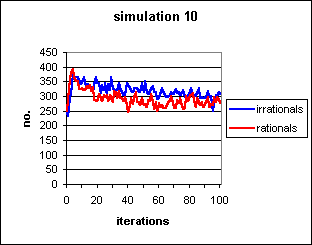
Figure 8: Non-contagion-dependent cultural system. The self-fulfilling prophecy maintains some degree of irrationality, but the ability of agents to convert away from irrationality without contact with a rational agent prevents it from running to fixation. Again, s=0.5, b=0.3.
Note that in Fig.8 the starting parameters
are s=0.5, b=0.3. By reference to Fig.
5, it can be seen that these would normally cause both memes to run
to fixation. This is indeed the initial tendency (note the initial rapid
upsurge in both blue and red lines), but the communal information then
begins to pull the meme frequencies down towards a quasi-random walk around
an equilibrium level.
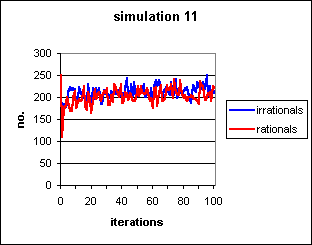
Figure 9: Same conditions as simulation 10, but allowing replacement of successful pairs. The initial dip is caused by the arrival of the first set of naïve agents in the first cycle or so before the cultural system has adequate data concerning the likely success of various pairs.
As in simulation 10, the cultural pool
requires a few iterations to establish its influence, this time after a
very short initial spell (almost invisible on Fig. 9)
where the downward tendency of simulation 8 is
repeated. This precipitate drop recovers almost immediately as the common
cultural pool begins to exert its influence.
The strictly contagionist person-to-person replication of both the rational and irrational behaviour is shown by simulation 8 to be unstable in the face of removal of individuals from the population. Indeed, even when all individuals are retained in the population, irrational behaviour requires the `self-fulfilling prophecy' phenomenon to spread through the population, as illustrated in the difference between simulations 4 and 5. Self-fulfilling prophecies have been empirically demonstrated in human mate pairing (involving `rejection-sensitivity' rather than astrology, but the basic principle is the same - see Downey et al 1998).
The only way to maintain the irrational behaviour in the population in the face of high levels of replacement is to use some kind of common information pool system. This, however, requires that the agents choose to refer to the information system for guidance. If, for some reason, the population in simulation 11 neglects to maintain the information system, the dynamics of simulation 8 will begin to take over and both memes will slide towards extinction.
It is clear that a `random walk' pattern of meme incidence over the iterations is more common than the `contagionist paradigm' sigmoid curve, which only occurs in rather `pure' situations. Random walk-like effects may be genuinely random because of the stochastic nature of the system (simulation 3), because of balanced rules in a deterministic system (simulation 4), or be anchored pseudo-random walks because of fluctuations around an equilibrium (simulations 10 and 11). Good `epidemiological' sigmoid curves in culture seem to require either arbitrary contagiousness (simulations 1 and 2), or a powerful selective force (the unopposed self-fulfilling prophecy of simulation 5). Some aspects of human life may be arbitrarily contagious, for example crowd hysteria (see reviews by Levy & Nail 1993; Marsden 1998). Several authors have worked within the `contagionist paradigm', producing models of traits that spread in an epidemic manner. For instance, Takahasi (1998, 1999) refers to `biased cultural transmission', Cavalli-Sforza and Feldman (1984) to `cultural selection', and Sperber (1985, 1996) to the `epidemiology of representations'. In these cases, it is taken for granted that the epidemic trait is either arbitrarily contagious or, in the case of Cavalli-Sforza and Feldman's `cultural selection', that some powerful, and usually unspecified, psychological factor is promoting the spread of the trait. The self-fulfilling prophecy phenomenon of simulation 5 would presumably therefore be a case of `cultural selection'. Another example might be `prestige-based transmission' (Heinrich 2001) where certain individuals are far more widely copied than others, or `emotional selection' (Heath et al 2001). Blackmore (1999) gives extensive further examples. Cavalli-Sforza and Feldman (1984) also refer to `natural selection' on culture, where a cultural trait spreads through genuine adaptiveness in the absence of either arbitrary `biased cultural transmission' or psychological `cultural selection'. Powerful natural selective forces of this kind do indeed also operate in culture, resulting in some sigmoid incidence curves for possession of, in modern times, mobile phones and other useful paraphernalia (Rogers 1995), or, in the Bronze Age, for bronze knives (Renfrew 1987). Hewlett and Cavalli-Sforza (1983) describe an epidemic spread of the use of the crossbow among Pygmies, conferring a great hunting advantage over the traditional bow and arrow.
Granted that cultural epidemics can, in theory, occur where there is natural or cultural selection (and certainly do occur for cases of natural selection), the question here is: to what extent could the contagionist paradigm be applied to (non-hysterical) irrationality? If most irrationality is disadvantageous (and therefore unlikely to be `naturally selected', sensu Cavalli-Sforza & Feldman, as an adaptation), and it is not the result of hysteria (and therefore not likely to have greatly biased transmission over a short time period), and the human society concerned has ample recourse to a pool of experience of previous members, then the spread of irrationality in an epidemic manner would seem to be unlikely. The contagionist paradigm therefore seems to be an inadequate model for the long term persistence of irrational behaviour in human populations.
For instance, in a stock market system, agents could predict the future price of shares, and then bid for them irrationally (perhaps again based on astrology) or rationally (based on profit indicators). If the purchase of shares causes their price to be elevated, this constitutes a kind of `self-fulfilling prophecy' phenomenon. This would tend to result in irrational bidding spreading throughout the entire investment community. The fact that this does not happen too often, is perhaps due to there being a well established communal information pool about the success of various previous investments, on which current investment decisions can be based. As in simulation 10, this would prevent even a strong `self-fulfilling prophecy' of irrational share inflation from taking over entirely. Interestingly, Caginalp et al (2001) have identified lack of open factual information as a contributory element in `bubbles' created during lab simulations of stock market trading. Such a situation would promote information exchange on a person to person basis and therefore lead to a greater susceptibility to contagion effects. Study of real markets has also led to the conclusion that the "level and nature of information available to dealers, and social communication networks" are important (reviewed in Marsden 1998, section 2). Empirical data shows that random walking does tend to predominate over long periods of time (Malkiel 1985). It is also interesting that although the common information pool helps to prevent irrationality running to fixation, it does not eliminate it. Just as evolution in financial markets does not lead to maximal market efficiency (Frank 1999), evolution in the mating game, or in any other area of human conduct, does not lead to maximal rationality. Heinrich (2001b) presents an interesting example of the persistence of bottle-feeding in parts of the world where breast-feeding would result in lower infant mortality. One might also cite Rogers and Shoemaker's classic example of the determination of Peruvian villagers not to boil drinking water despite extensive health education and the established use of boiling for other food purposes (Rogers & Shoemaker 1972), or recent discussions of `altruistic punishment' (Fehr & Gachter 2002) and the revival of the `tragedy of the commons' debate (Ostrom et al. 1999, Henrich et al 2001a). Henrich (2001b) finds that the persistence of maladaptive behaviour is most likely when: a) there is high probability that environmental information is inconclusive, and b) there is biased transmission of the maladaptive trait. This is entirely consonant with the simulations presented here. Interestingly and rather controversially, Henrich goes a step further and suggests that even adaptive traits require biased transmission in order to produce S-shaped curves. This is a radical departure from the fundamental theoretical observation that natural selection of an advantageous trait is analogous in form to an epidemic, and produces an S-shaped curve (Fisher 1930). It is not appropriate to discuss this any further here other than to note that the present observations concerning the cultural information pool and the relative rarity of situations in which the contagionist paradigm applies, are consonant with the first part of Henrich's (2001b) thesis.
One point not covered in the simulations is the issue of spatial heterogeneity within the population. The simulations could be modified to give each individual a geographical location. Partner choice, and the extent of the cultural information pool, could thus be limited by geographical isolation. One might also permit the high status individuals greater geographical mobility than those of the low status. Multi-generational effects might allow some of the successfully mated individuals to produce offspring for reintroduction into the population at a later date. Incorporation of a genetic component might also be permitted, with some individuals being inherently more or less sceptical than others.
In summary, the contagionist paradigm is a special case scenario, only applicable to situations of:
Blackmore S (1999) The Meme Machine.
Oxford University Press, Oxford.
Boyd R & Richerson PJ (1985). Culture and the Evolutionary Process. The University of Chicago Press, Chicago.
Brown PS, Humm RD & Fischer RB (1988) The influence of a male's dominance status on female choice in Syrian hamsters. Hormonal Behavior 22, 143-149.
Caginalp G, Porter D & Smith V (2001) Financial Bubbles: Excess Cash, Momentum, and Incomplete Information. Journal of Psychology and Financial Markets 2. (http://www.psychologyandmarkets.org/journals/abstracts/issue_v2_2.html).
Cavalli-Sforza LL & Feldman MW (1981) Cultural Transmission and Evolution. Princeton University Press, Princeton.
Darwin C (1871) The Descent of Man, and Selection in Relation to Sex, 2 volumes. John Murray, London.
Delfabbro PH & Winefield AH (2000) Predictors of irrational thinking in regular slot machine gamblers. Journal of Psychology 134, 117-128.
Doran J (1998) Simulating Collective Misbelief. Journal of Artificial Societies and Social Simulation 1 (http://www.soc.surrey.ac.uk/JASSS/1/1/3.html).
Downey G, Freitas AL, Michaelis B &
Khouri H (1998) The self-fulfilling prophecy in close relationships: rejection
sensitivity and rejection by romantic partners. Journal of Personality
and Social Psychology 75, 545-560.
Durham WH (1991) Coevolution: Genes, Culture and Human Diversity. Stanford University Press, Stanford.
Edmonds B (1998) On Modelling in Memetics. Journal of Memetics - Evolutionary Models of Information Transmission 2 (http://cfpm.org/jom-emit/1998/vol2/edmonds_b.html).
Fehr E & Gachter S (2002) Altruistic punishment in humans. Nature 415, 137-40
Fisher RA (1930) The Genetical Theory of Natural Selection. Clarendon Press, Oxford.
Frank J (1999) Applying Memetics to Financial Markets: Do Markets Evolve towards Efficiency? Journal of Memetics - Evolutionary Models of Information Transmission 3 (http://cfpm.org/jom-emit/1999/vol3/frank_j.html).
Freeberg TM, Duncan SD, Kast TL & Enstrom DA (1999) Cultural influences on female mate choice: an experimental test in cowbirds, Molothrus ater. Animal Behavior 57, 421-426.
Goodkind DM (1993) New zodiacal influences on Chinese family formation: Taiwan, 1976. Demography 30, 127-42.
Heath C, Bell C & Sternberg E (2001)
Emotional selection in memes: the case of urban legends. Journal of
Personality
and Social Psychology 81, 1028-1041.
Henrich J & Boyd R (1998) The evolution of conformist transmission and the emergence of between-group differences. Evolution and Human Behavior 19, 215-241.
Henrich J, Boyd R, Bowles S, Camerer C, Fehr E, Gintis H & McElreath R (2001a) In Search of Homo Economicus: Behavioral Experiments in 15 Small-Scale Societies. American Economic Review 91, 73-78.
Henrich J (2001b) Cultural Transmission and the Diffusion of Innovations: Adoption Dynamics Indicate That Biased Cultural Transmission Is the Predominate Force in Behavorial Change. American Anthropologist 103, 992-1013.
Hewlett BS & Cavalli-Sforza LL (1983) Cultural transmission among Aka pygmies. American Anthropologist 88, 922-934.
Kimura M (1979) The neutral theory of molecular evolution. Scientific American 241, 98-108.
Kimura M & Ohta T (1978) Stepwise mutation model and distribution of allelic frequencies in a finite population. Proceedings of the National Academy of Sciences USA 75, 2868-2872.
Laland KN (1994) Sexual selection with a culturally transmitted mating preference. Theoretical Population Biology 45, 1-15.
Levy DA & Nail PR (1993) Contagion:
a theoretical and empirical review and reconceptualization. Genetic,
Social and General Psychology Monographs 119, 233-284.
Lindeman M (1998) Motivation, cognition and pseudoscience. Scandinavian Journal of Psychology 39, 257-265.
Malkiel BG (1985) A Random Walk Down Wall Street. 4th ed. Norton, New York.
Marsden P (1998). Memetics and Social Contagion: Two Sides of the Same Coin? Journal of Memetics - Evolutionary Models of Information Transmission2 (http://cfpm.org/jom-emit/1998/vol2/marsden_p.html).
Ophir S (1998) Simulating Ideologies. Journal of Artificial Societies and Social Simulation 1 (http://www.soc.surrey.ac.uk/JASSS/1/4/5.html).
Ostrom E, Burger J, Field CB, Norgaard RB & Policansky D (1999) Revisiting the commons: local lessons, global challenges. Science 284, 278-282.
Pearson DW & Boudarel M-R (2001) Pair Interactions : Real and Perceived Attitudes. Journal of Artificial Societies and Social Simulation 4 (http://www.soc.surrey.ac.uk/JASSS/4/4/4.html).
Pizzari T (2001) Indirect partner choice through
manipulation of male behaviour by female fowl, Gallus gallus domesticus.
Proceedings
of the Royal society of London Series B, Biological
Sciences 268, 181-186.
Rashevsky N (1949) Mathematical biology of social behaviour I. Bulletin of Mathematical Biophysics 11, 105-113.
Renfrew C (1987) Archaeology & Language: The Puzzle of the Indo-European Origins. Jonathan Cape, London
Rogers EM & Shoemaker FF (1971) Communication of Innovations. A Cross-cultural Approach 2nd ed. Free Press, New York.
Rogers EM (1995) The Diffusion of Innovations 4th ed. The Free Press, New York.
Schnitzler A (1982) The round dance and other plays. Arthur Schnitzler. trans. and intro. Osborne, C. Carcanet New Press, Manchester.
Sperber D (1985) Anthropology and psychology: towards an epidemiology of representations. Man, 73-89.
Sperber D (1996) Explaining Culture: A Naturalistic Approach. Blackwell, Oxford.
Takahasi K (1998) Evolution of transmission bias in cultural inheritance. Journal of Theoretical Biology 190, 147-59.
Takahasi K (1999) Theoretical aspects of the mode of transmission in cultural inheritance. Theoretical Population Biology 55, 208-25
Wade MJ & Pruett-Jones SG (1990) Female copying increases the variance in male mating success. Proceedings of the National Academey of Sciences USA 87, 5749-5753.