 Butts, C. T.and
Hilgeman, C. (2003). Inferring Potential Memetic Structure
from Cross-Sectional Data: An Application to American Religious Beliefs.
Butts, C. T.and
Hilgeman, C. (2003). Inferring Potential Memetic Structure
from Cross-Sectional Data: An Application to American Religious Beliefs.
Journal of Memetics - Evolutionary Models of Information Transmission,
7.
http://cfpm.org/jom-emit/2003/vol7/butts_ct&hilgeman_c.html
Inferring Potential Memetic Structure from Cross-Sectional Data: An
Application to American Religious Beliefs
Carter T. Butts* and Christin Hilgeman+
*Department of Sociology
and Institute for Mathematical
Behavioral Sciences
University of California, Irvine
[note 1]
buttsc@uci.edu
+Department of Sociology;University of California, Irvine
Abstract:
The identification and measurement of
memes poses a fundamental challenge for research in memetics. Recent
methodological developments regarding inference for latent algebraic
structure provide a useful tool for inferring potential memetic
structure from cross-sectional data. Here, we perform such an analysis
on selected items from the 1988 and 1998 General Social Survey religion
modules. American religious belief over the period is shown to be
stable, with a complex structure which is reducible neither to a set of
distinct scales nor to a model of itemwise independence. A decomposition
of observed behavioral characters into latent meme-like constructs
reveals underlying connections between otherwise disparate items, and
demonstrates the presence of several interlocking scale-like structures.
Interpretations of the resultant latent structures are provided, and
some possible implications for the memetic theory of religion are
discussed.
Keywords: meme theory,
microbelief analysis, latent class analysis, religious beliefs
Meme theory has a number of potential strengths: it provides an
intuitive way of connecting biology, culture, and the environment; it
offers explanations for a wide range of social phenomena; and it is
amenable to formal modeling (see, e.g., 13,11). As compelling as these
factors may be, meme theory has a grave difficulty in practice: much of
its long-term utility hinges upon the identification and measurement of
memes (or at least small memeplexes). This - the problem of memetic
inference - is a significant challenge. Unlike genes, which can be
studied directly, memes are not available to inspection. (Indeed, there
is considerable controversy over the precise definition of the meme
itself (20,33,37).) Typically,
empirical memetic accounts rely on an intuitive specification of memes,
often working on the assumption that the underlying memes are synonymous
with their behavioral characters (or artifactual traces thereof); see,
for instance, (8,24,16). This is
problematic, however, since many cultural phenomena of substantive
interest involve a complex of interconnected beliefs which exhibit
mutual dependence (32,26).
How, then, can we hope to proceed? As it happens, the history of
genetics itself suggests an answer: well before the discovery of DNA,
the genetic system was studied by indirect inference from associations
among characters (31). Within sociology,
indirect inference has also been used by Martin
and Wiley (28) to infer the presence of "microbeliefs" from survey
response data via the application of a latent lattice [note 2] model developed
by Haertel and Wiley (18). (Such
work is part of a long tradition of latent structure models in the
social sciences, including classic work by Lazarsfeld and Henry (23); Goodman (14,15); Guttman (17), among
many others.) As we shall illustrate, the latent structure model of
Martin and Wiley can be employed to uncover "meme-like" structures in
cross-sectional data sets. These structures consist of inferred latent
elements ("candidate memes" or "quasi-memes") whose conjunction (i.e.,
combination by AND logic) is associated with the manifestation of
behavioral characters. Thus, any given character - for instance, a
professed belief in the Judeo-Christian god - is presumed to manifest
within a given individual if (and only if) all of its requisite
quasi-memes are present. Just as characters may depend upon multiple
quasi-memes, so too may a given quasi-meme contribute to multiple
characters; thus, potentially complex patterns of dependence may be
inferred within the set of characters, the set of quasi-memes, and the
two taken jointly.
The approach pursued here is explicitly cross-sectional, and thus we
emphasize that the quasi-memes uncovered by this method should be
considered only as candidates for subsequent examination by
intertemporal methods. Similarly, one can posit complex expression
mechanisms (e.g., incorporating XOR or NOT logic) which cannot be
inferred by this technique. Where potential memetic structures can be
identified using the latent lattice model, however, the model may
subsequently be employed to produce estimates of the individual
incidence of quasi-memes (i.e., which quasi-memes are held by which
persons). These estimates may then be used longitudinally and/or in
experimental settings to test for transferability of the potential
memetic elements, and thereby to confirm or deny a hypothesis of genuine
memetic structure. (Some suggestions for such follow-on studies are
discussed in Section 3 below.) Because the
initial "screening" of candidate memes under this method can be
performed on large data sets, substantially greater statistical power
can be brought to bear on the problem than would be possible in more
traditional settings. Furthermore, the use of cross-sectional data
greatly facilitates the study of representative samples from whole
populations, thereby improving the prospects for successful examination
of large-scale memetic ecologies. As such ecologies are of significant
interest to theorists in the field (e.g., 1,13,7), it is hoped that this capability will
facilitate more empirically informed development in this area.
We begin our discussion of the latent lattice model by assuming that
we have identified a set of behavioral characters which span some domain
of interest, and that we have obtained measures on those characters for
a sample of individuals drawn at random from a given population. [note 3] (For our present
purposes, we shall limit ourselves exclusively to binary characters.)
Consider, for instance, a set of characters associated with responses to
a standard survey instrument (e.g., agree/disagree items relating to
sexual behavior). Under Martin and Wiley's model, each individual's
pattern of responses to such a series of (dichotomous) items is modeled
as arising from a conjunction of latent dichotomous subelements.
Specifically, if 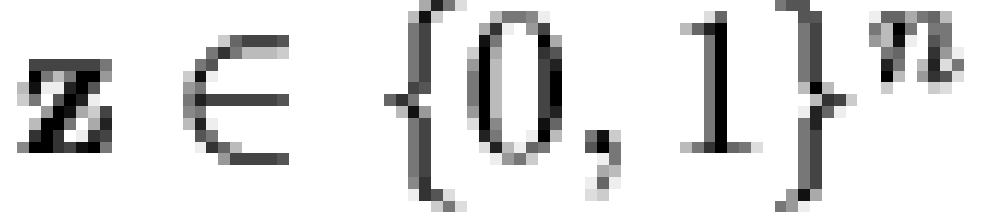 is a vector of
"microbeliefs,"
is a vector of
"microbeliefs," 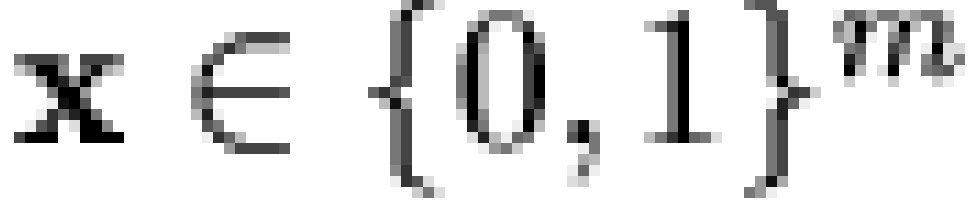 is a vector
of responses (or "macrobeliefs"), and
is a vector
of responses (or "macrobeliefs"), and 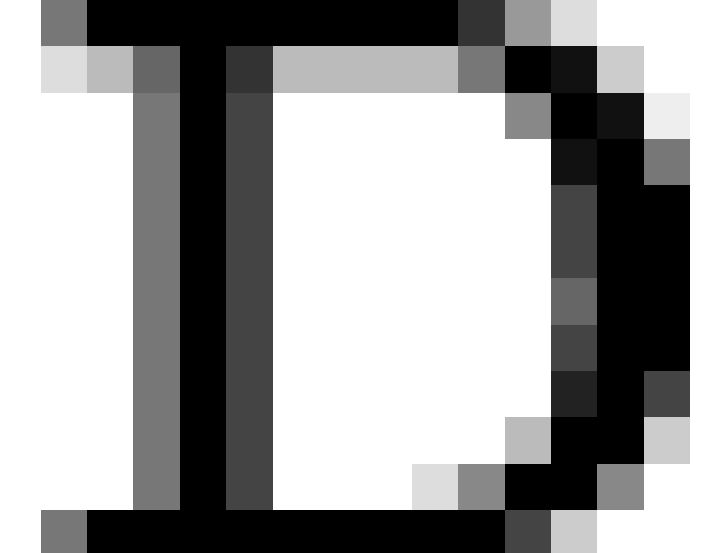 is an
is an 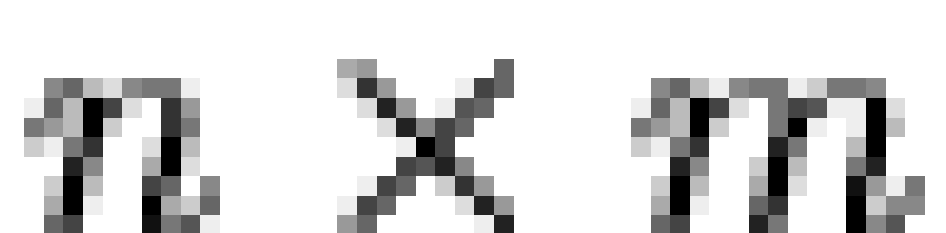 dichotomous dependency matrix, then it is
assumed that
dichotomous dependency matrix, then it is
assumed that
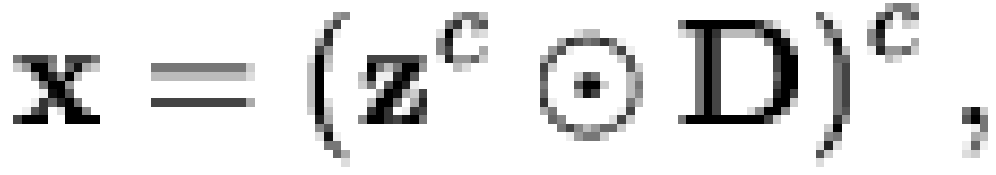 |
(1) |
where  represents the Boolean inner
product and
represents the Boolean inner
product and  is the Boolean complement
operator. Thus, a given individual is predicted to hold macrobelief
is the Boolean complement
operator. Thus, a given individual is predicted to hold macrobelief 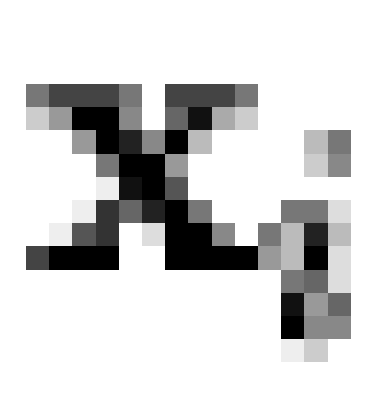 if and only if they hold all microbeliefs
if and only if they hold all microbeliefs 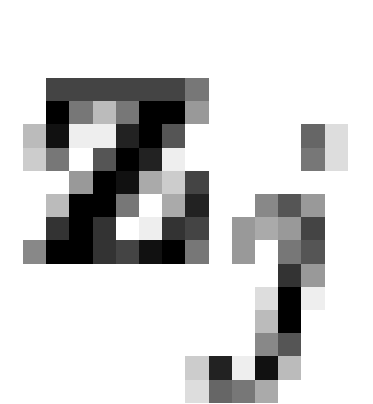 such that
such that 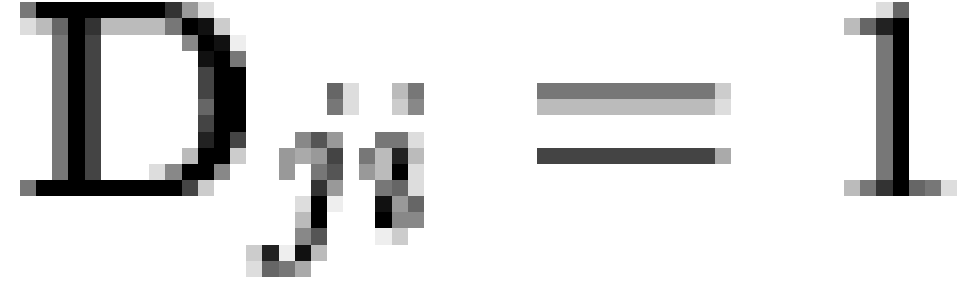 . Generally, we
also assume that the columns of
. Generally, we
also assume that the columns of  are 1-covered, and that
are 1-covered, and that  has no identical rows. (Obviously,
has no identical rows. (Obviously,  is defined only up to a row permutation.)
Under such a model, it can be shown that the set of observable
macrobelief states forms a lattice (28);
more importantly, given a lattice of observed macrobelief states, the
inversion of Haertel and Wiley (18)
can be employed to recover the
is defined only up to a row permutation.)
Under such a model, it can be shown that the set of observable
macrobelief states forms a lattice (28);
more importantly, given a lattice of observed macrobelief states, the
inversion of Haertel and Wiley (18)
can be employed to recover the  matrix (and latent
matrix (and latent  vectors). Let
vectors). Let  be a matrix whose rows contain all
observable macrobelief states for some
be a matrix whose rows contain all
observable macrobelief states for some  , and define a row
, and define a row  to be a
meet-irreducible element (MIRE) of
to be a
meet-irreducible element (MIRE) of  iff
iff 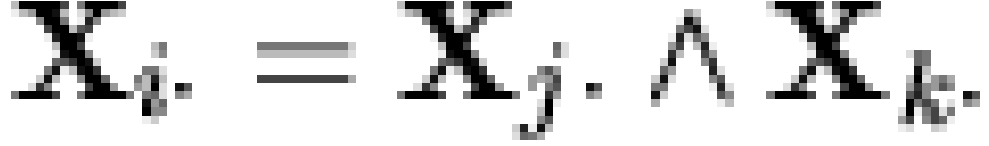 implies
implies 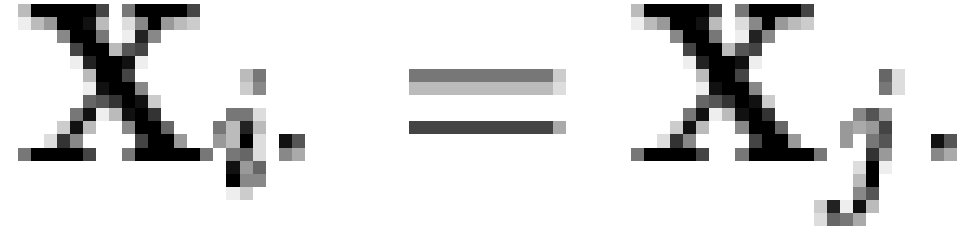 or
or 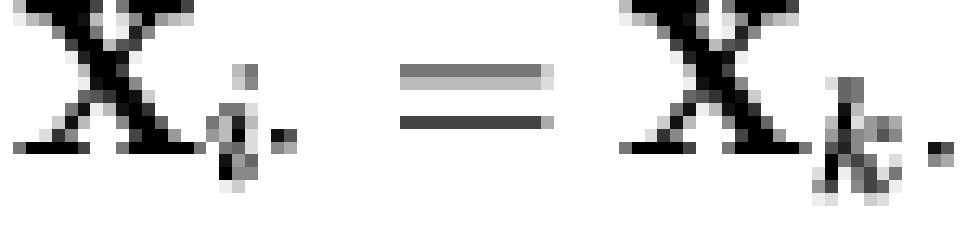 for all
for all 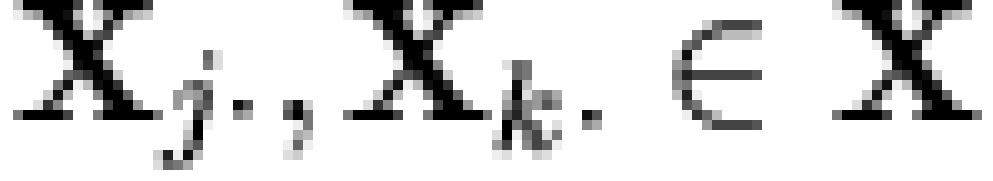 (where
(where 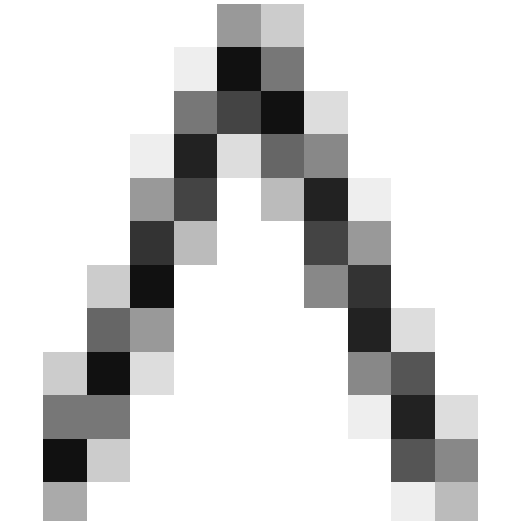 is the intersection operator [note 4]). If
is the intersection operator [note 4]). If 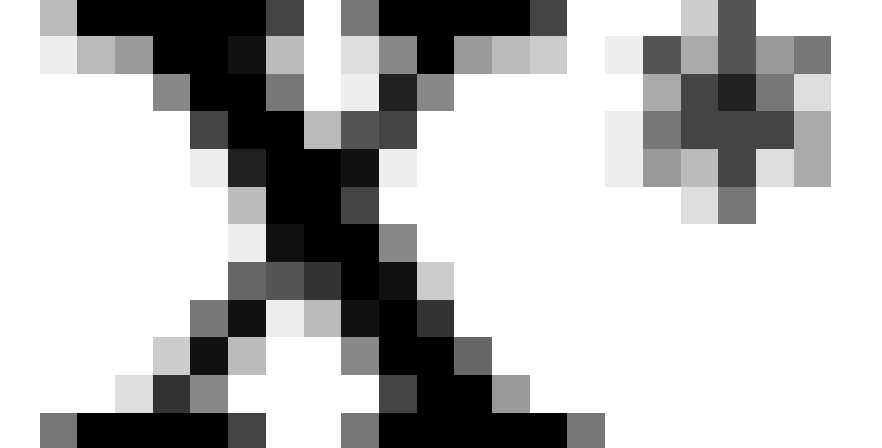 is a matrix whose rows contain the
MIREs of
is a matrix whose rows contain the
MIREs of 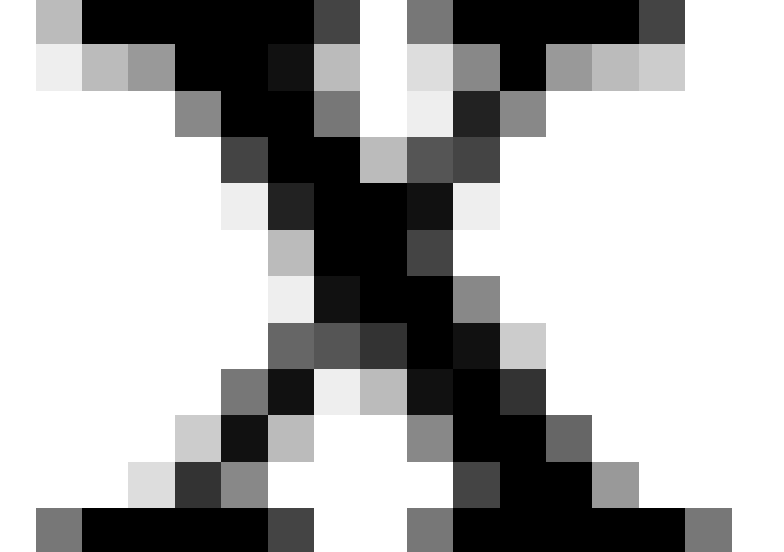 , then
, then
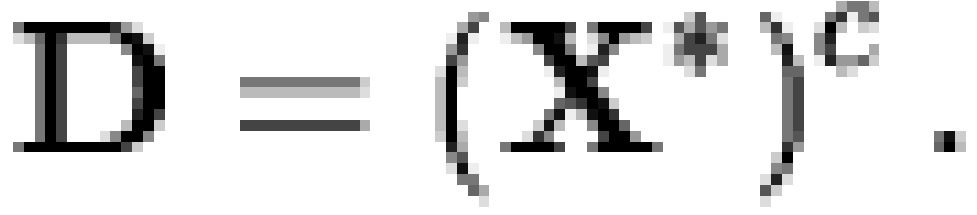 |
(2) |
Therefore, we can readily move from observed macrobelief states to
latent microbelief states, and vice versa. Of course, given real data,
we do not expect things to work quite so neatly. In addition to pure
measurement error, it is to be expected that the lattice model itself is
only an imperfect representation of the latent structure of individual
beliefs. For this reason, vectors of actual responses (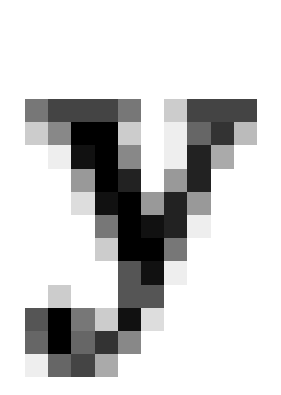 )
are treated by Wiley and Martin as arising from the true latent state (
)
are treated by Wiley and Martin as arising from the true latent state (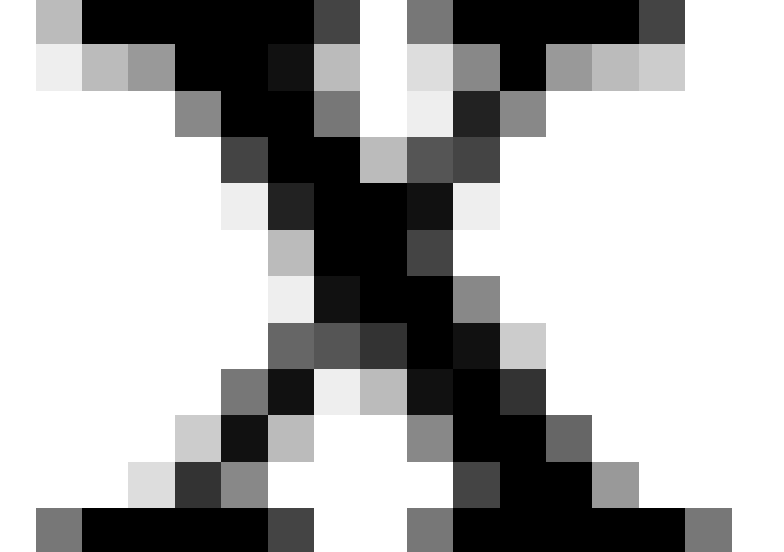 ) under an error model; as a practical
matter, this is treated as a problem of confirmatory latent class
analysis (29).
) under an error model; as a practical
matter, this is treated as a problem of confirmatory latent class
analysis (29).
The analogy between Martin and Wiley's microbelief analysis and meme
theory is striking. Martin and Wiley's "macrobeliefs" may be likened to
manifest behavioral characters, with the associated "microbeliefs"
presumably being the memes themselves. The 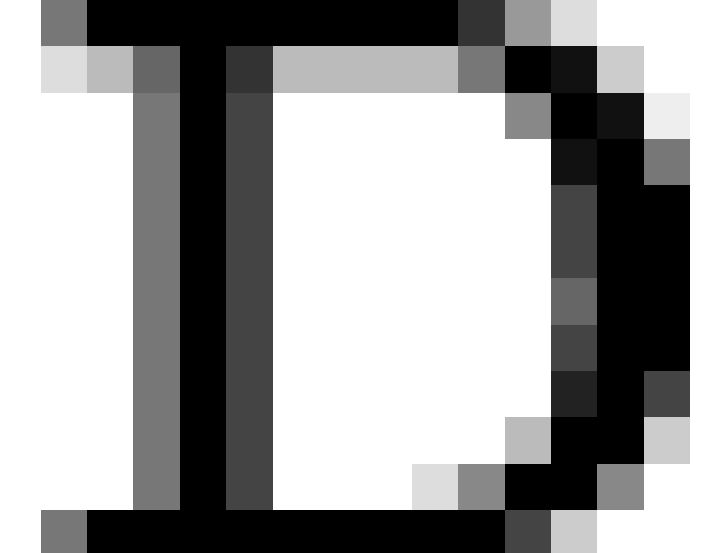 matrix (together with its associated
algebraic operations) provides the expression mechanism for the
underlying memes, converting memotype into behavioral phenotype. While
this phenotype may be thought of as reflecting manifest beliefs, it need
not be: specific behaviors, cultural practices, or the like are equally
admissible. Likewise, data for the analysis can be derived from human
subject experiments, direct observation, or inspection of artifacts as
well as survey instruments. As mentioned earlier, this method has some
significant limitations. It can only model expression by conjunctive
interaction, for instance, and cannot therefore detect memes whose
effects are inhibitory. Additionally, because it does not provide a
stochastic model for the underlying distribution of memes among
individuals, the procedure may not be robust to samples whose underlying
distribution of memes is extremely biased. Despite these limitations,
however, the method employed here provides an inferential framework
which can discern a reasonably broad class of latent structures in the
presence of limited measurement error. In applying it to the problem of
memetic inference, we proceed in the spirit of Hull's argument that an
effective operationalization of the notion of "meme" can "emerge only as
one sets about doing memetics" (20,
page 48). The formalism employed here cannot capture all conceivable
memetic structures, but it may still serve as an empirically useful
starting point.
matrix (together with its associated
algebraic operations) provides the expression mechanism for the
underlying memes, converting memotype into behavioral phenotype. While
this phenotype may be thought of as reflecting manifest beliefs, it need
not be: specific behaviors, cultural practices, or the like are equally
admissible. Likewise, data for the analysis can be derived from human
subject experiments, direct observation, or inspection of artifacts as
well as survey instruments. As mentioned earlier, this method has some
significant limitations. It can only model expression by conjunctive
interaction, for instance, and cannot therefore detect memes whose
effects are inhibitory. Additionally, because it does not provide a
stochastic model for the underlying distribution of memes among
individuals, the procedure may not be robust to samples whose underlying
distribution of memes is extremely biased. Despite these limitations,
however, the method employed here provides an inferential framework
which can discern a reasonably broad class of latent structures in the
presence of limited measurement error. In applying it to the problem of
memetic inference, we proceed in the spirit of Hull's argument that an
effective operationalization of the notion of "meme" can "emerge only as
one sets about doing memetics" (20,
page 48). The formalism employed here cannot capture all conceivable
memetic structures, but it may still serve as an empirically useful
starting point.
Given the potential of this new tool to uncover memetic structure
from empirical data, we here perform a microbelief analysis of data on
American religious practice and belief drawn from the General
Social Survey (GSS) for years 1988 and 1998 (6,5). While we cannot here demonstrate
transmissibility - a critical requirement of the theory - we can
nevertheless identify structures using the Martin and Wiley approach
which could serve as "candidate memes." These structures are inferred
from associations between manifest characters, reflecting a hypothetical
substrate which is consistent with the observed data. Having obtained a
set of hypothetical memes (and an associated expression mechanism), one
may then examine subjects longitudinally to determine whether or not
these elements are indeed the basic units of belief transmission. As
recent work by Markovsky and Thye (25)
has demonstrated, discrete beliefs regarding supernatural phenomena can
be transferred under laboratory conditions. [note 5] Thus, it is in principle feasible to
experimentally test the hypothesized meme structure, having initially
reduced the number of possible alternatives by cross-sectional study of
a large, nationally representative sample.
We begin our analysis with a discussion of the data set and the
coding scheme employed. We then compare the 1988 and 1998 samples, and
analyze general properties of the response distribution. Following this
we use a confirmatory latent class model to infer a lattice structure
from the religion data, and, finally, we perform a detailed structural
analysis of the inferred lattice (including an examination of the
potential latent memetic structure).
The data for this analysis come from the religion modules of the
1988 and 1998 General Social Survey (6,5). With the exception of questions
regarding friends, twelve items were asked of respondents at both time
points; these comprise the first twelve rows of Table 1. Of these items, one is an "empirical"
belief (GOD),
four are normative judgments (GOCHURCH, BELIEVE, FOLLOW, and GOOWNWAY),
five are interpretations of personal experiences (REBORN, DOUBTS1, DOUBTS2, FAITH1, and FAITH2), and
two are behavioral self-reports (SAVESOUL and READWORD).
Thus, the questions serve as a reasonably diverse collection of
behavioral characters. Rather less diverse is the span of topics
considered: three of the items deal explicitly with Christianity, seven
are more broadly Judeo-Christian, and eight are at least implicitly
monotheistic in nature. Thus, this sample does not allow us to study
issues relating to non-monotheist worldviews (including atheism,
pantheism, and polytheism), or to identify fine-grained beliefs
regarding non-Judeo-Christian monotheisms (e.g., Islam). Neither does
this sample focus on specific issues of denominational significance
(e.g., biblical inerrancy, creationism, variations in eschatology). With
this in mind, it may be most useful to consider these question items to
represent a moderately general sample of beliefs and behaviors relating
primarily to modern American Judeo-Christian religious practice. Latent
structures identified at this level may be subsequently elaborated via
more detailed questioning.
For each of the twelve initial questions, a dichotomous coding was
constructed which differentiated positive assertions (coded 1) from a
lack of the same (coded 0). (Where "don't know" responses could be
identified with the lack of an assertion, these were coded 0. Otherwise,
such responses were treated as missing data.) A brief description of the
coded items is provided in Table 1.
As noted above, the set of questions asked of respondents at both
time points involved a series of items regarding the religious beliefs
and practices of friends nominated by the respondent. Although the data
does not permit the type of diffusion analysis which would be ideal for
meme-theoretic purposes, it nevertheless provides us with additional
information regarding the respondent. With this in mind, we constructed
a thirteenth item, FRNDCON, which
was coded as 1 if the respondent indicated having at least one friend
who was a member of his or her congregation, and 0 otherwise.
(Respondents not belonging to a congregation were also coded 0.)
For the 1988 and 1998 samples, 1481 and 1445 respondents
(respectively) were asked the twelve questions (plus friendship)
employed here. Removing all cases containing missing data reduced the
respective totals to 1384 and 1150. With thirteen dichotomous variables,
the number of potential response patterns was 8192 (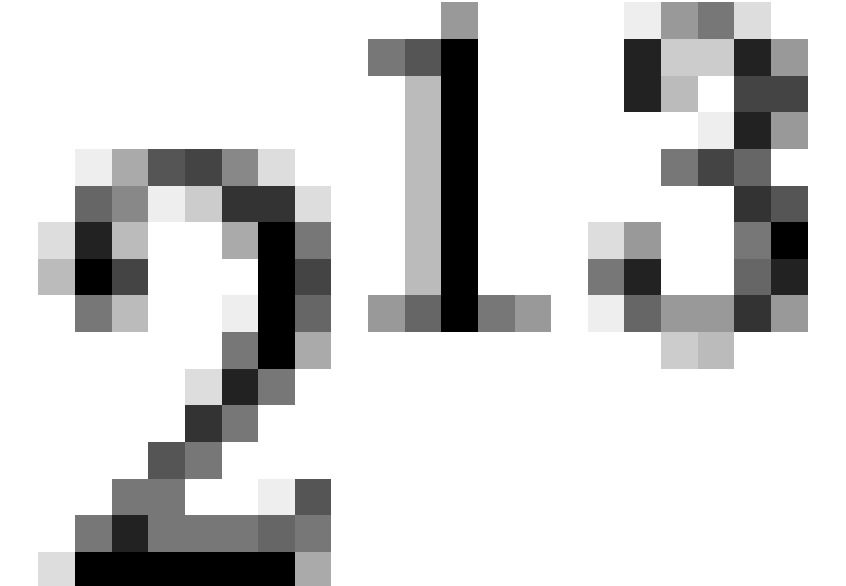 ), of
which 718, 646, and 1056 were observed for the 1988, 1998, and combined
samples (respectively). Our analysis, then, centers on the frequencies
of these behavioral phenotypes, and on their associated characters.
), of
which 718, 646, and 1056 were observed for the 1988, 1998, and combined
samples (respectively). Our analysis, then, centers on the frequencies
of these behavioral phenotypes, and on their associated characters.
Table 1: Description of
coded GSS items
| Item |
Description |
| GOD |
Believes in a personal god, at least some
of the time |
| GOCHURCH |
Believes that regular religious service
attendance is important to being a good Christian or Jew |
| BELIEVE |
Believes that believing in god without
doubt is important to being a good Christian or Jew |
| FOLLOW |
Believes that faithfully following
church/synagogue teachings is important to being a good Christian or Jew |
| GOOWNWAY |
Believes that following one's conscience
(even against church/synagogue) is important to being a good Christian
or Jew |
| REBORN |
Believes self to have had a born again
experience |
| SAVESOUL |
Reports attempting to convert others to
Christianity |
| READWORD |
Reports reading the Bible at home within
the last year |
| DOUBTS1 |
Reports evil in the world has never caused
religious doubts |
| DOUBTS2 |
Reports personal suffering has never
caused religious doubts |
| FAITH1 |
Reports religious faith strengthened by
death in family on some occasion |
| FAITH2 |
Reports religious faith strengthened by
birth of a child on some occasion |
| FRNDCON |
Reports belonging to and having at least
one friend in own congregation |
|
The first question which presents itself regarding behavioral
phenotypes for American religious belief over the 1988-1998 interval is
that of structural stability: is there evidence of substantial change in
the distribution of phenotypes, or is the frequency distribution
constant over the period (for these characters, at least)? With this in
mind, we begin our analysis by comparing the distribution of observed
phenotypes in the 1988 sample with that observed in 1998.
Taking the 8192 possible response patterns, we begin by accumulating
the frequency distribution of observed response states for each sample.
A simple  test of homogeneity indicated no significant
difference between the distributions (1070.039 on 8191 degrees of
freedom,
test of homogeneity indicated no significant
difference between the distributions (1070.039 on 8191 degrees of
freedom,  ). Due to the sparseness
of the sample, additional tests were performed as well. A Monte Carlo
). Due to the sparseness
of the sample, additional tests were performed as well. A Monte Carlo  conditioning on row/column marginals with 5000 replicate
draws [note 6] did not
indicate significant differences between the samples
(p>0.998),
nor did similar tests of the L1 (the absolute difference - sometimes
called "manhattan" metric in reference to city block distances), L2
(Euclidean distance), maximum norm, or rank correlation (all
conditioning on row/column marginals with 5000 replicate
draws [note 6] did not
indicate significant differences between the samples
(p>0.998),
nor did similar tests of the L1 (the absolute difference - sometimes
called "manhattan" metric in reference to city block distances), L2
(Euclidean distance), maximum norm, or rank correlation (all 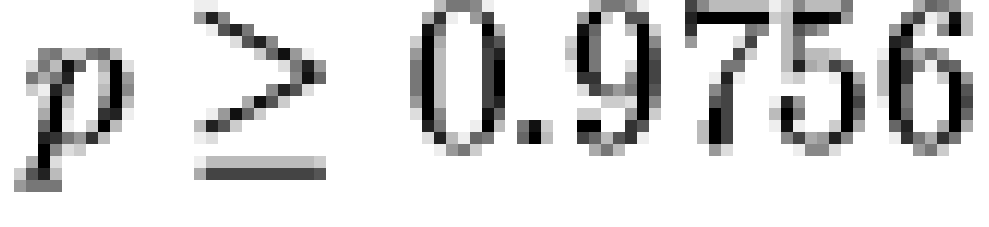 ). Taken together,
these tests suggest that any observed deviations between the 1988 and
1998 phenotype distributions are typical of what would be expected by
chance variation, and that this conclusion is quite robust to choice of
similarity measure.
). Taken together,
these tests suggest that any observed deviations between the 1988 and
1998 phenotype distributions are typical of what would be expected by
chance variation, and that this conclusion is quite robust to choice of
similarity measure.
Another indication of the strong correspondence between
distributions is provided by the similarity of rank structure among the
most commonly observed patterns. Specifically, let us take 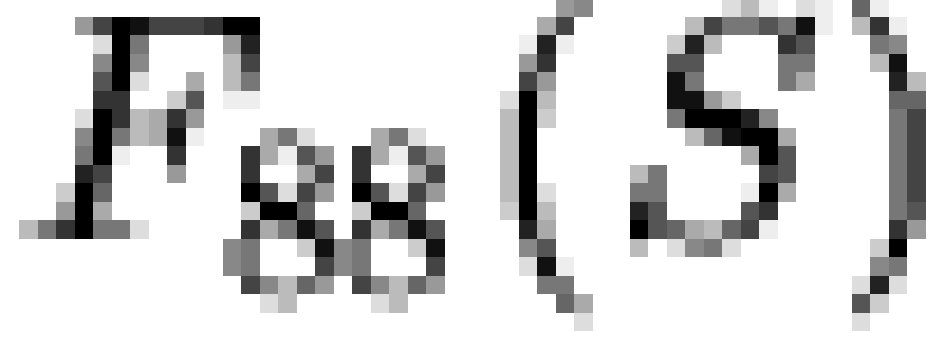 to be the fraction of
cases from the 1988 sample accounted for by pattern set
to be the fraction of
cases from the 1988 sample accounted for by pattern set 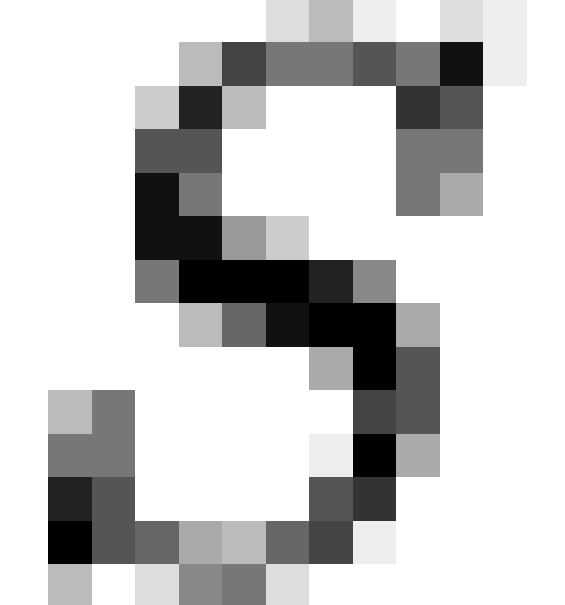 (with
(with 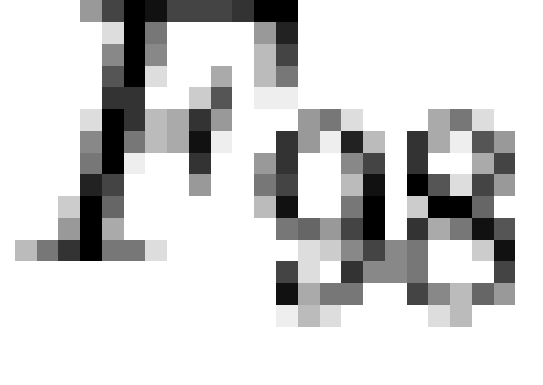 defined analogously). Next,
we define
defined analogously). Next,
we define  and
and  to be the set of all
patterns for the 1988 and 1998 samples (respectively) having (ascending)
sample rank less than or equal to
to be the set of all
patterns for the 1988 and 1998 samples (respectively) having (ascending)
sample rank less than or equal to  . Given this, the "coverage ratios"
. Given this, the "coverage ratios" 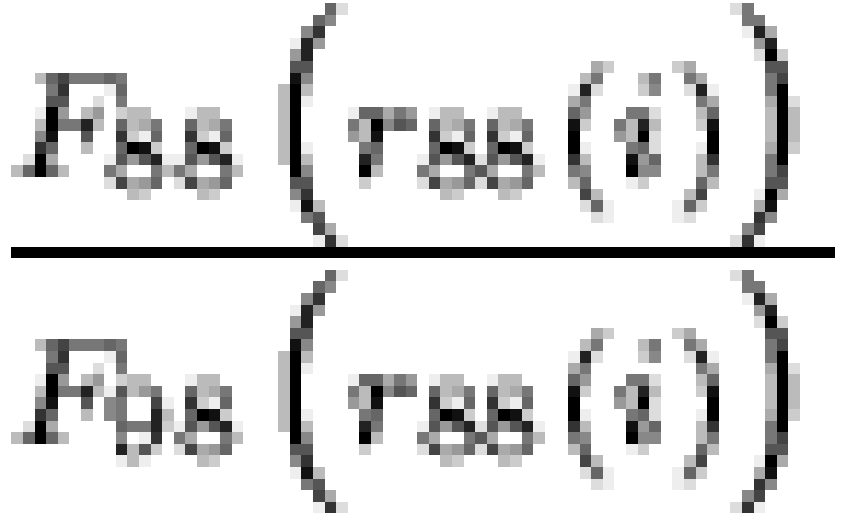 and
and 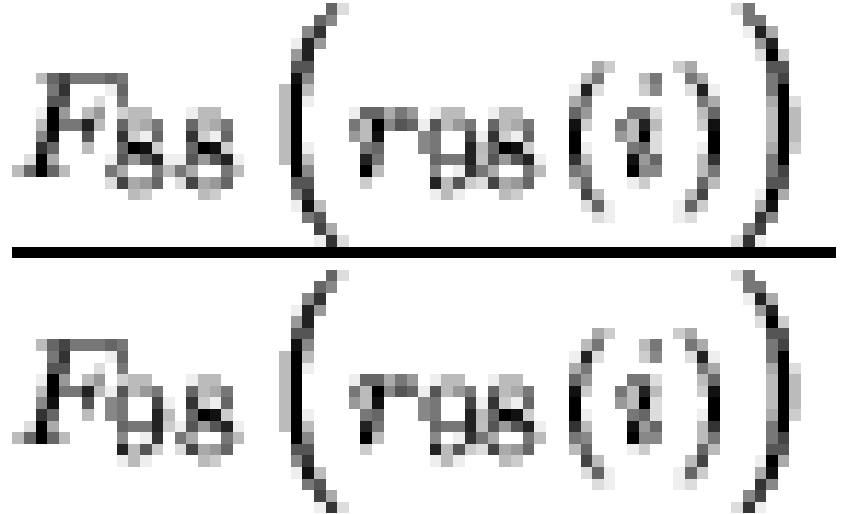 can be used to assess the detailed agreement of the two
distributions regarding the most frequent cases. Where the two
distributions are precisely equal, both coverage ratios are equal to 1;
as the distributions deviate from equality, the ratios will shift
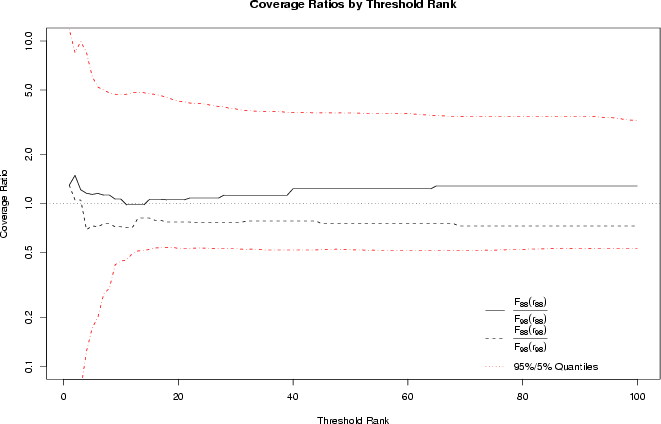
correspondingly. Plots of coverage ratios for the GSS
religion data are shown in Figure 1 for
ranks one through one hundred. For reference, 95% and 5% quantiles have
also been shown for the upper and lower ratios (respectively), based on
5000 Monte Carlo replications of the data set fixing marginal totals. As
can be seen, the coverage ratios remain reasonably close to 1 throughout
the interval, indicating 1) that the same patterns are common in both
samples, and 2) that these patterns account for a fairly similar
proportion of their respective samples. The observed coverage ratios are
also well within the natural range of variability which might be
anticipated by the margins alone, further suggesting that the observed
deviation is not extreme. This further reinforces the result of the more
general test procedures, indicating that belief patterns for the two
samples do not differ greatly overall, nor in regions of high
probability.
can be used to assess the detailed agreement of the two
distributions regarding the most frequent cases. Where the two
distributions are precisely equal, both coverage ratios are equal to 1;
as the distributions deviate from equality, the ratios will shift
correspondingly. Plots of coverage ratios for the GSS
religion data are shown in Figure 1 for
ranks one through one hundred. For reference, 95% and 5% quantiles have
also been shown for the upper and lower ratios (respectively), based on
5000 Monte Carlo replications of the data set fixing marginal totals. As
can be seen, the coverage ratios remain reasonably close to 1 throughout
the interval, indicating 1) that the same patterns are common in both
samples, and 2) that these patterns account for a fairly similar
proportion of their respective samples. The observed coverage ratios are
also well within the natural range of variability which might be
anticipated by the margins alone, further suggesting that the observed
deviation is not extreme. This further reinforces the result of the more
general test procedures, indicating that belief patterns for the two
samples do not differ greatly overall, nor in regions of high
probability.
Figure 1: Coverage ratios for
1988 and 1998 phenotype distributions, by threshold rank (PDF Version)
 |
The finding that - for these characters - American religious belief
was fairly stable over the period from 1988-1998 would seem to suggest
that the present questions tap into relatively "deep" belief structures
whose distributional properties change (at best) slowly with time. In
order to uncover these general latent structures, then, we combine the
two samples for the analyses which follow.
Combining the religious belief data for the 1988 and 1998 samples,
we first investigate the global population distribution across the set
of possible behavioral phenotypes. To what extent, for instance, is the
distribution heavily concentrated on a small number of realized states,
versus being widely dispersed? How does the state frequency decay as one
moves from the most frequent to the least frequent states? While they do
not deal with the properties of particular characters, the answers to
such questions nevertheless provide information regarding what sort of
process may have given rise to the observations at hand.
In answer to the first question, we note that the estimated entropy
for the phenotype distribution [note 7]
is approximately 9.28 bits, substantially below the 13 bits associated
with the uniform density. Put another way, we can immediately discern
that the information content of the observed phenotype distribution is
slightly in excess of the maximum for 9 binary characters, signifying
just under a 4 character "redundancy" (or an entropy reduction of 29%).
This suggests a fairly high degree of concentration in the distribution,
which we display visually in Figure 2.
Figure 2 provides a log-log plot of the
frequency of each observed phenotype, sorted in descending order of
probability density; a least-squares line has been provided for
reference. As the linear fit suggests, the observed frequency
distribution decays approximately as a power law over much of its range ( ,
, 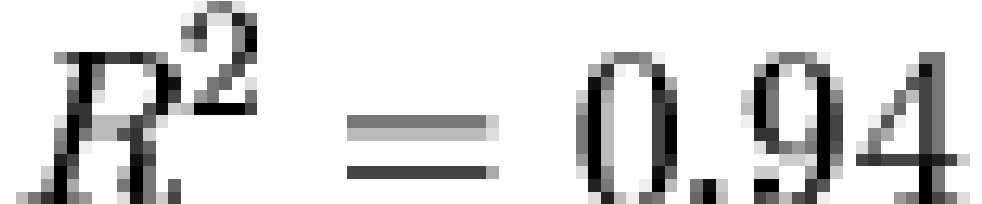 ). Although some minor deviations are
present (partially due to granularity effects), the relationship is
clearly not exponential in form (
). Although some minor deviations are
present (partially due to granularity effects), the relationship is
clearly not exponential in form (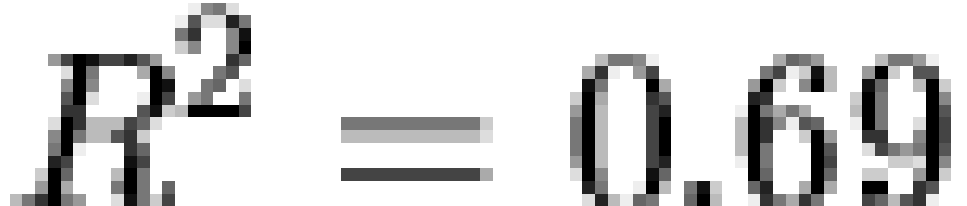 ). Thus, the overall frequency distribution
displays an extremely high degree of concentration on the most common
values, combined with a "long tail" of numerous patterns observed in
only a few instances. This should be contrasted with an equivalent
exponential model, in which less concentration would be observed on the
most common patterns, coupled with a lighter tail.
). Thus, the overall frequency distribution
displays an extremely high degree of concentration on the most common
values, combined with a "long tail" of numerous patterns observed in
only a few instances. This should be contrasted with an equivalent
exponential model, in which less concentration would be observed on the
most common patterns, coupled with a lighter tail.
Figure 2: Frequency
distribution of phenotypes (combined GSS data) and
95% Monte Carlo confidence intervals, independence model (PDF Version)
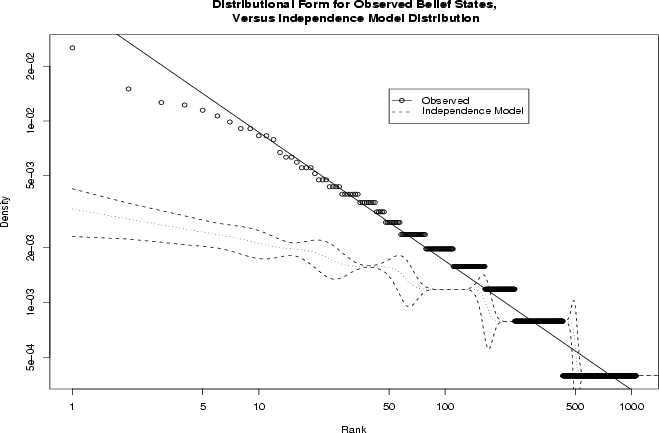 |
This observed pattern of extreme concentration strongly suggests
underlying configural structure in the data; in particular, it is
interesting to note that models based on itemwise independence tend to
produce exponential frequency distributions. To compare against one such
model, Figure 2 shows the mean and 95% Monte
Carlo confidence interval for the replicate frequency distributions
under an independence model with character frequencies matching the
observed data (50,000 replications). The null frequency distribution is
clearly different in form from the observed frequency distribution,
decaying roughly exponentially rather than as a power law. Furthermore,
the observed distribution is far beyond the 95% confidence interval for
the independence model over the vast majority of its range, suggesting
that the latter is not a credible model for the former. Thus, we see
from examining the overall distribution of behavioral phenotypes that 1)
the population distribution is highly structured, and 2) this structure
cannot be accounted for by raw character frequencies alone. We now
proceed to an investigation of the underlying configural properties of
the combined belief data.
To uncover latent configural structure in the combined GSS
data, we employ the microbelief analysis strategy of Martin and Wiley (27,28). In this
context, this technique centers on the identification of a lattice of
phenotypes - a set of phenotypic states which is closed under
intersection of characters - such that the observed distribution of
states can be be expressed in terms of the lattice together with a
simple error process. To accomplish this, a "candidate lattice" is
initially formed from the original data set, and is subsequently fit to
the observed phenotype distribution via confirmatory latent class
analysis (29). Multiple candidate
lattices may be evaluated in this manner, with the final choice being
made by optimization of some prespecified model fit criterion e.g., the
Akaike's Information Criterion (AIC) or Bayesian
Information Criterion (BIC) [note 8]. The selected model may then be
compared against other, non-lattice alternatives, and/or analyzed in
other respects. Here, we shall focus on the latent class analysis of the GSS
belief data; a detailed structural analysis of the inferred lattice
structure will be performed in the succeeding section.
The general procedure employed was as follows. For 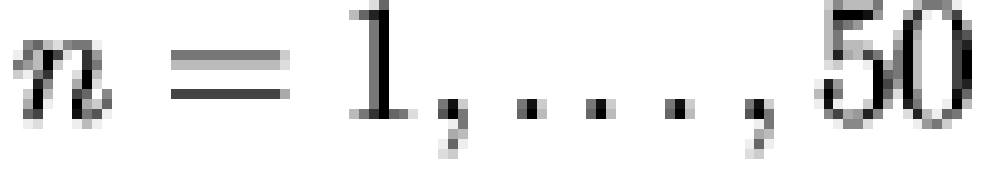 , the
, the 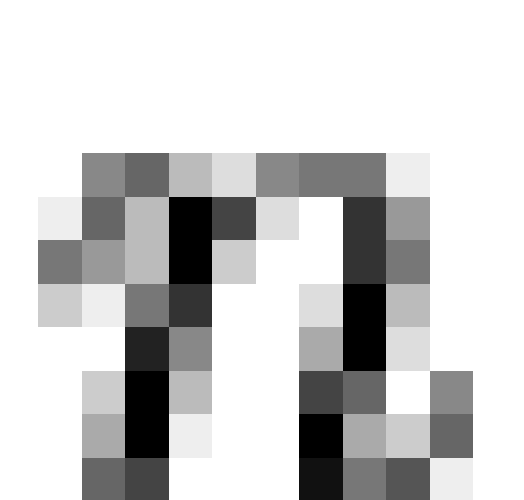 most frequent patterns were extracted from the
combined data set and closed under intersection to form a lattice (
most frequent patterns were extracted from the
combined data set and closed under intersection to form a lattice ( 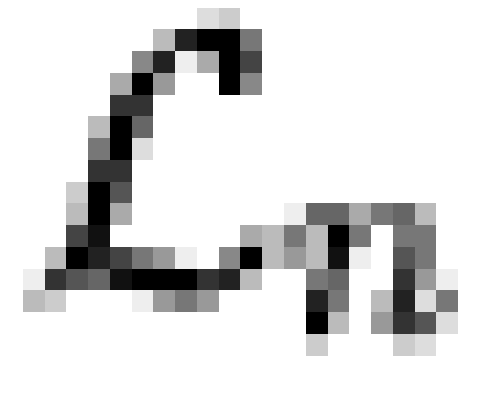 ). A confirmatory
latent class model with itemwise false positive/false negative error
parameters (29) was fit for each such
lattice, and the associated model selection statistics retained. (Note
that all estimates shown are maximum likelihood
estimators.) Finally,
). A confirmatory
latent class model with itemwise false positive/false negative error
parameters (29) was fit for each such
lattice, and the associated model selection statistics retained. (Note
that all estimates shown are maximum likelihood
estimators.) Finally, 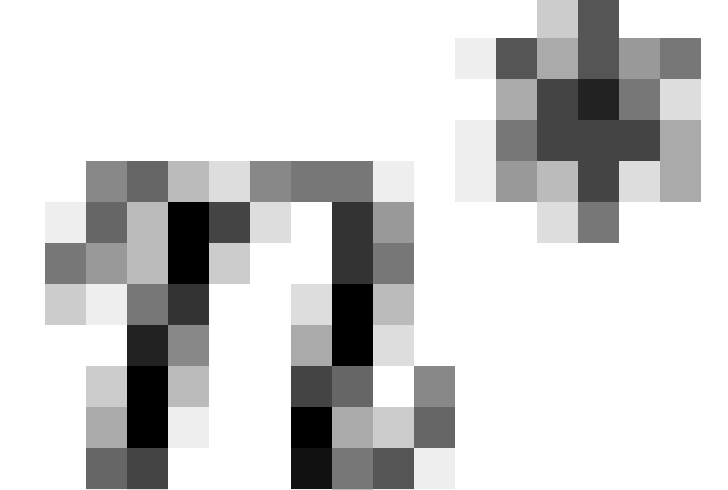 was selected such that the BIC
of the model on
was selected such that the BIC
of the model on 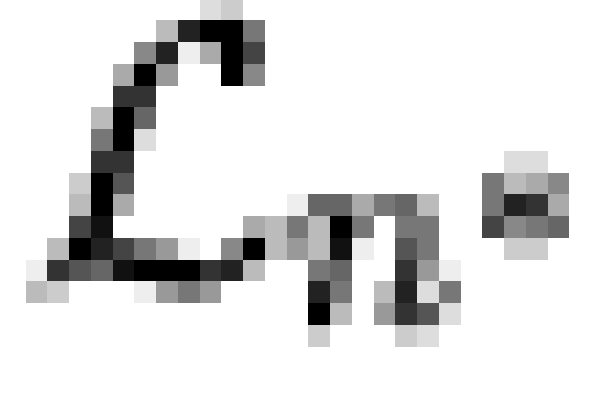 was minimized. For
the combined GSS
religion data,
was minimized. For
the combined GSS
religion data, 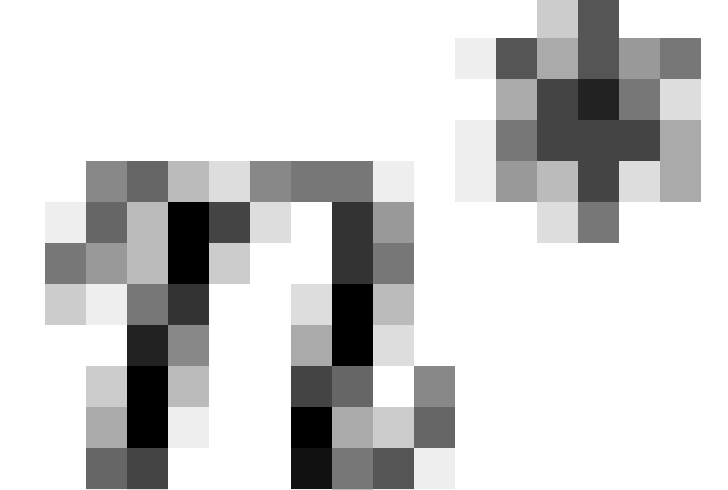 was found to equal 25, resulting in a lattice of
size 55. The elements of this lattice (represented as binary strings)
along with estimated class probabilities are shown in Table 2. Note that although only 25 of the lattice
elements were drawn from the data (the rest being constructed via
closure), 40 of the elements are estimated to have non-negligible rates
of incidence in the population. This demonstrates that the closure
operation is able to uncover viable phenotypic states [note 9], but the
zero-weight patterns are of substantive interest as well. Such patterns
reflect phenotypes which are admissible under the assumed memetic
model, but which are essentially unobserved within the
population. These "empty" states may reflect the action of a social
process such as clustering (22),
which renders certain admissible combinations of beliefs more probable
than others, or they may result from some as yet unidentified process.
By providing a baseline against which to compare our observations, the
lattice model may be able to aid in the discovery of new social
phenomena.
was found to equal 25, resulting in a lattice of
size 55. The elements of this lattice (represented as binary strings)
along with estimated class probabilities are shown in Table 2. Note that although only 25 of the lattice
elements were drawn from the data (the rest being constructed via
closure), 40 of the elements are estimated to have non-negligible rates
of incidence in the population. This demonstrates that the closure
operation is able to uncover viable phenotypic states [note 9], but the
zero-weight patterns are of substantive interest as well. Such patterns
reflect phenotypes which are admissible under the assumed memetic
model, but which are essentially unobserved within the
population. These "empty" states may reflect the action of a social
process such as clustering (22),
which renders certain admissible combinations of beliefs more probable
than others, or they may result from some as yet unidentified process.
By providing a baseline against which to compare our observations, the
lattice model may be able to aid in the discovery of new social
phenomena.
Table 2: Estimated
class probabilities, combined GSS data
| Phenotype |
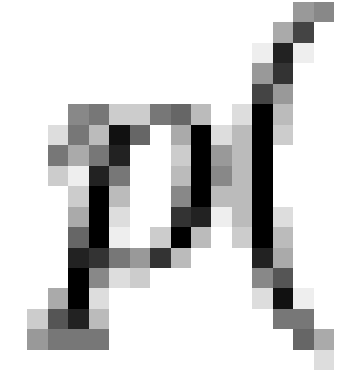 state state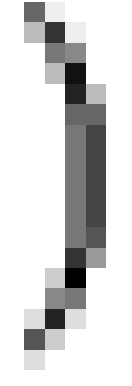 |
Phenotype |
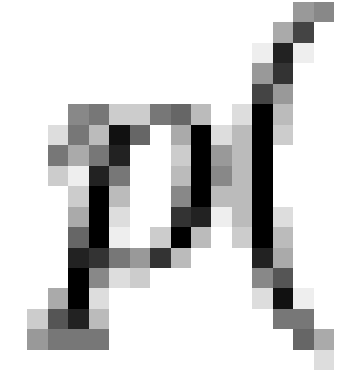 state state |
| 0000000000000 |
0.0159 |
1010001100110 |
0.0230 |
| 1000000000000 |
0.0250 |
1111001100110 |
0.0036 |
| 0000100000000 |
0.0305 |
1010011100110 |
0.0192 |
| 1000100000000 |
0.0001 |
1111011100110 |
0.1160 |
| 0000000010000 |
0.0000 |
1010111100110 |
0.0382 |
| 1000000010000 |
0.0000 |
1111111100110 |
0.0029 |
| 0000100010000 |
0.0000 |
1111000110110 |
0.0000 |
| 1000100010000 |
0.0077 |
1111100110110 |
0.0000 |
| 0000000011000 |
0.0304 |
1111001110110 |
0.0000 |
| 1000000011000 |
0.0381 |
1111011110110 |
0.0000 |
| 0000100011000 |
0.0182 |
1111111110110 |
0.0000 |
| 1000100011000 |
0.0159 |
1111000111110 |
0.0387 |
| 0000000000010 |
0.0000 |
1111100111110 |
0.0098 |
| 1000000000010 |
0.0000 |
1111001111110 |
0.0000 |
| 1010000000010 |
0.0000 |
1111011111110 |
0.0703 |
| 0000100000010 |
0.0040 |
1111111111110 |
0.0037 |
| 1000100000010 |
0.0130 |
1111000100111 |
0.0196 |
| 1010100000010 |
0.0002 |
1111100100111 |
0.0039 |
| 0000000000110 |
0.0334 |
1111001100111 |
0.0153 |
| 1000000000110 |
0.0707 |
1111011100111 |
0.0664 |
| 1010000000110 |
0.0553 |
1111111100111 |
0.0048 |
| 0000100000110 |
0.0227 |
1111001110111 |
0.0000 |
| 1000100000110 |
0.0386 |
1111011110111 |
0.0177 |
| 1010100000110 |
0.0009 |
1111111110111 |
0.0000 |
| 1010000100110 |
0.0000 |
1111001111111 |
0.0095 |
| 1111000100110 |
0.0358 |
1111011111111 |
0.0548 |
| 1010100100110 |
0.0000 |
1111111111111 |
0.0109 |
| 1111100100110 |
0.0153 |
|
|
 probability probability 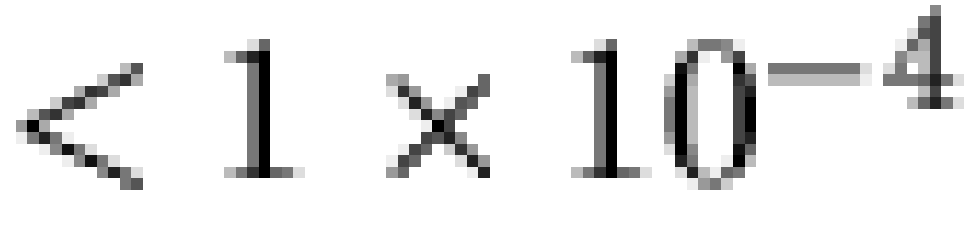 |
|
As noted above, the model employed was a confirmatory latent class
analysis with itemwise asymmetric error probabilities. Estimates for
these probabilities are provided in Table 3.
Note that with very few exceptions, the estimated error rates are quite
low, indicating that most observations are quite close to the lattice.
False positive probabilities were found to be somewhat higher than false
negative probabilities in general, suggesting that deviations from the
lattice were more often in the direction of reporting too many beliefs
rather than too few. Such asymmetries may reflect differential
availability of error opportunities, as well as a general demand effect
for reporting high levels of religiosity (given the cultural
significance placed on religion within the United States).
Table 3: Estimated
error probabilities by character, combined GSS data
| Character |
 false
neg false
neg |
 false
pos false
pos |
| GOD |
0.0192 |
0.1373 |
| GOCHURCH |
0.2088 |
0.0817 |
| BELIEVE |
0.0554 |
0.3490 |
| FOLLOW |
0.1422 |
0.2241 |
| GOOWNWAY |
0.0001 |
0.4887 |
| REBORN |
0.1636 |
0.0658 |
| SAVESOUL |
0.1163 |
0.1042 |
| READWORD |
0.1722 |
0.3140 |
| DOUBTS1 |
0.0000 |
0.2709 |
| DOUBTS2 |
0.0000 |
0.2392 |
| FAITH1 |
0.2305 |
0.1271 |
| FAITH2 |
0.1309 |
0.1109 |
| FRNDCON |
0.0022 |
0.1987 |
 probability probability 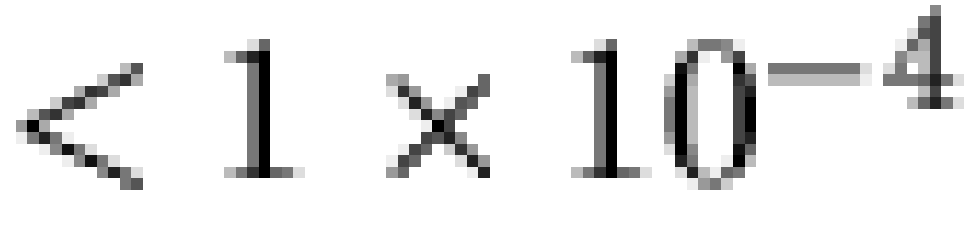 |
|
Model fit statistics for the optimal lattice model, along with
several reference models, are shown in Table 4.
In addition to the saturated model, the fit statistics are shown for
the null model of independence and a Guttman scale (17). The Guttman scale constitutes an
obvious null model of unidimensional structure, and was here implemented
as a confirmatory latent class model in the same manner as the general
lattice model above [note 10]
(35). (The Guttman scale itself was
constructed using item frequencies.) As Table 4
indicates, the unrestricted lattice model is comfortably favored over
all three reference models by both the AIC
and BIC.
Likelihood ratio tests against the saturated model fail to reject both
the unrestricted lattice and Guttman scale models (  in both cases), with the
former showing a significant improvement over the latter (
in both cases), with the
former showing a significant improvement over the latter (  ). Taken together, these
results indicate that: the lattice model is an acceptable representation
of the data; the unrestricted lattice is substantially superior to a
simple, unidimensional structure; and the unrestricted lattice is also
substantially superior to a null model of itemwise independence.
). Taken together, these
results indicate that: the lattice model is an acceptable representation
of the data; the unrestricted lattice is substantially superior to a
simple, unidimensional structure; and the unrestricted lattice is also
substantially superior to a null model of itemwise independence.
Table 4: Model fit
statistics, combined GSS Data
| |
|
Residual |
Likelihood |
|
|
| Model |
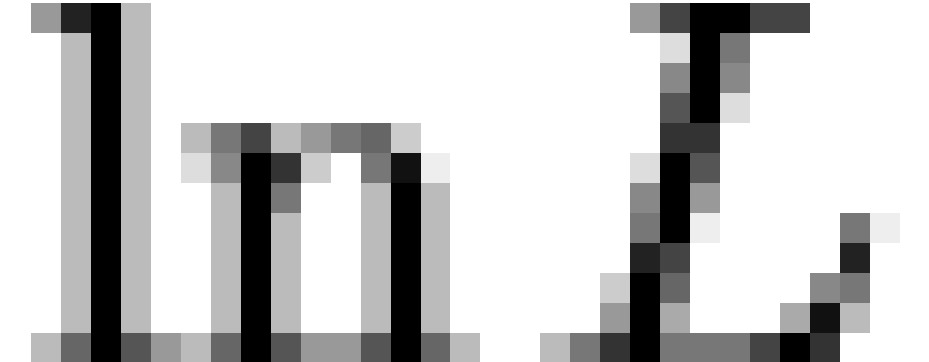 |
Df |
Ratio  |
AIC |
BIC |
| Saturated Model |
-16300.12 |
0 |
0 |
48982.24 |
96797.65 |
| Lattice Model |
-18281.96 |
8110 |
3963.685 (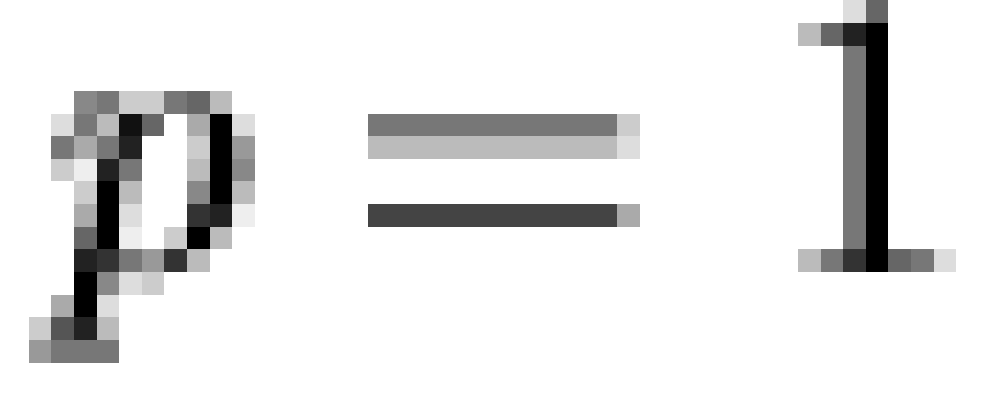 ) ) |
36725.93 |
37198.77 |
| Guttman Scale |
-19041.04 |
8151 |
5481.835 (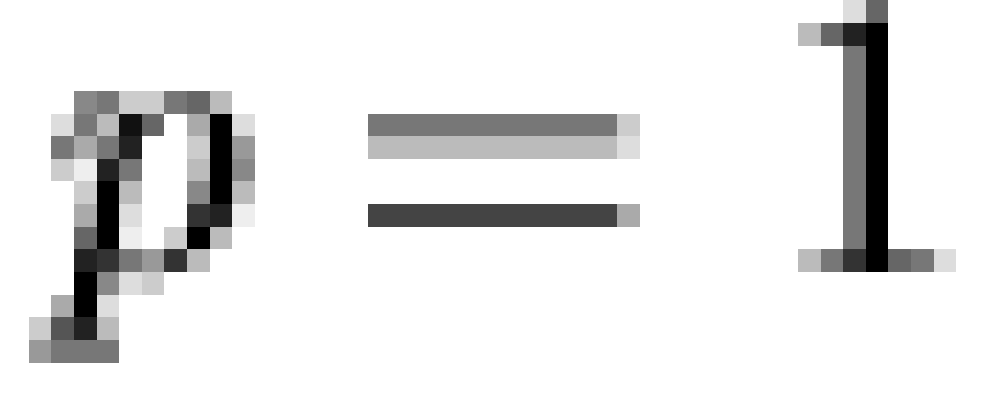 ) ) |
38162.07 |
38395.58 |
| Null Model |
-21143.36 |
8178 |
9686.488 (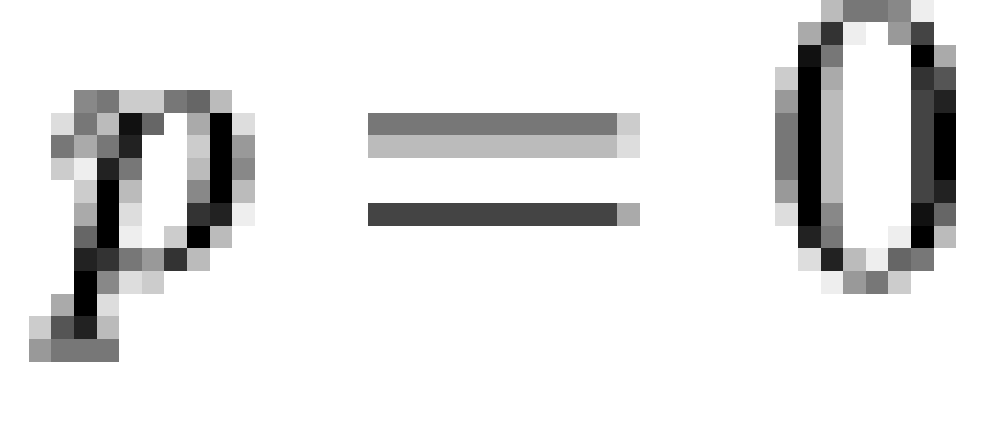 ) ) |
42312.72 |
42388.62 |
|
Having inferred a lattice for the combined GSS
belief data, we now perform a detailed structural analysis of the
lattice itself. Strictly speaking, the lattice is merely a small,
idealized set of response patterns which are assumed to lie behind the
complete set of observed response patterns. By closely examining this
set, however, we may uncover various relationships between behavioral
characters. Furthermore, because this set is (by construction) a lattice,
it follows that we can identify a dual set of items such that the
former can be formed out of the latter by an operation of conjunction as
described in Equation 2 (28,18). It is the
elements of this dual set which serve as our "candidate" memes, for the
simple reason that each observed character can be seen as arising from
the interaction of one or more such elements. By analyzing the
relationships between behavioral characters and the inferred memes, [note 11] then, we hope
to uncover latent structural properties of the religious belief system.
These properties may, in turn, suggest secondary procedures to test the
hypothesis that the candidate memes are, in fact, genuine units of
social replication.
Note that, in keeping with the fundamental duality of the
memotype/phenotype set, the inferred memes are non-trivially structured
as well. Formally, the memotype set is a distributive lattice,
which in the present context indicates that it is closed under union and
intersection (28). Less formally, we
may be interested in relations among memes such as precedence,
in which one meme is held [note 12]
only if another is held first. By studying such relationships among
inferred memes, we may gain insight into their empirical interpretation.
We begin our analysis by employing the Haertel-Wiley inversion (28,18) to extract
the mapping from memotypes to behavioral phenotypes (the 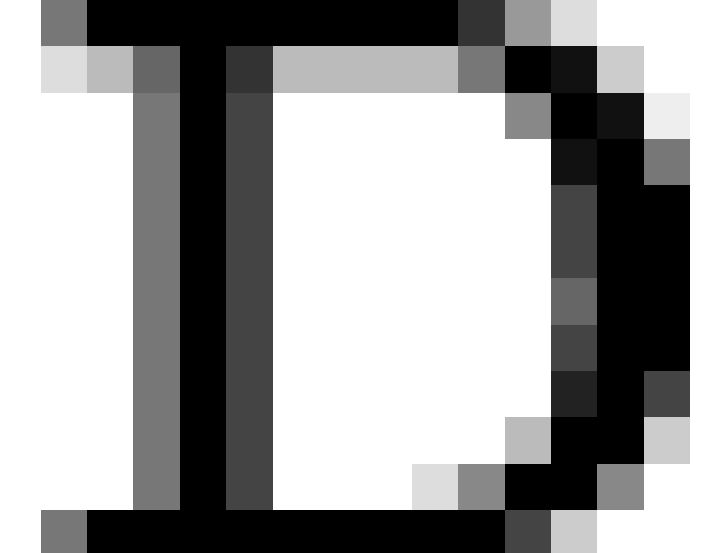 matrix) from the lattice of phenotypic
states. The
matrix) from the lattice of phenotypic
states. The 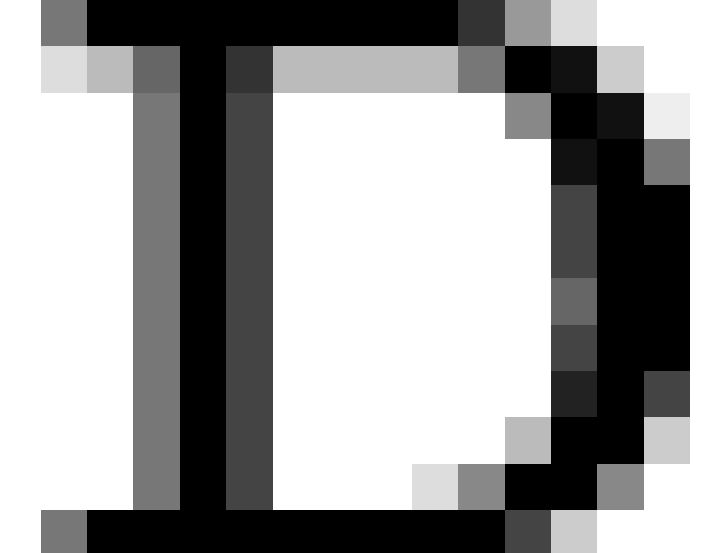 matrix for the combined GSS
religion data is shown in Table 5.
Interpretation of the
matrix for the combined GSS
religion data is shown in Table 5.
Interpretation of the 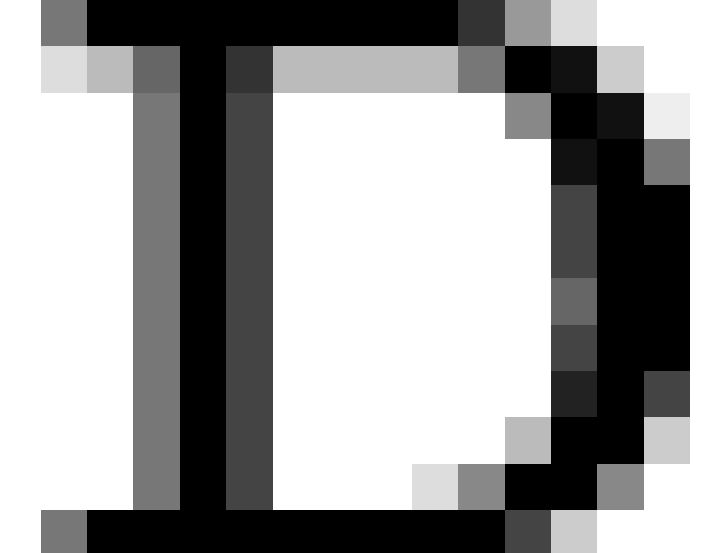 matrix is as follows:
matrix is as follows: 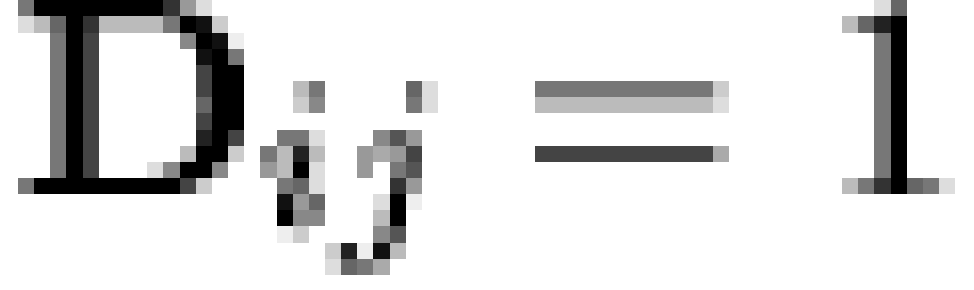 if and only if
character
if and only if
character 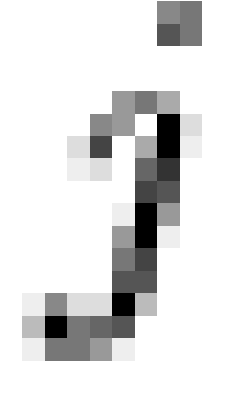 depends on meme
depends on meme 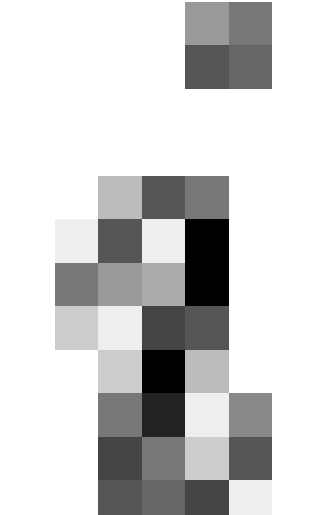 , and an individual will exhibit a given character
if and only if he or she holds all memes on which said character
depends. The
, and an individual will exhibit a given character
if and only if he or she holds all memes on which said character
depends. The 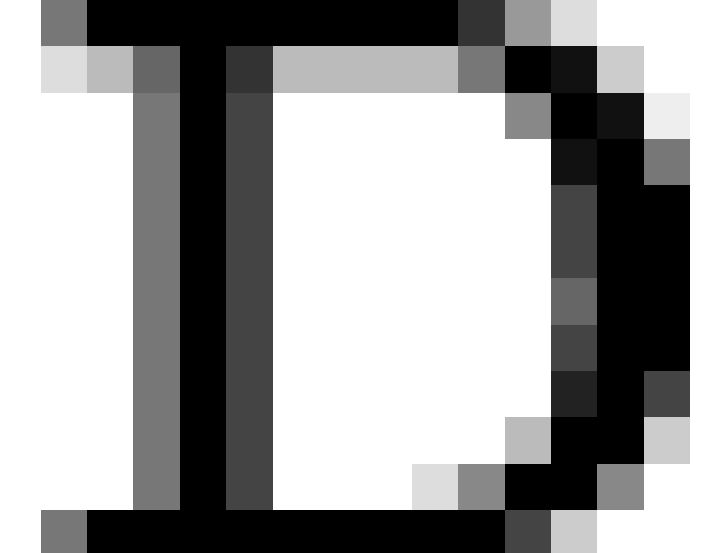 matrix thus encodes the putative expression mechanism for the
underlying meme system.
matrix thus encodes the putative expression mechanism for the
underlying meme system.
Table 5:
Inferred 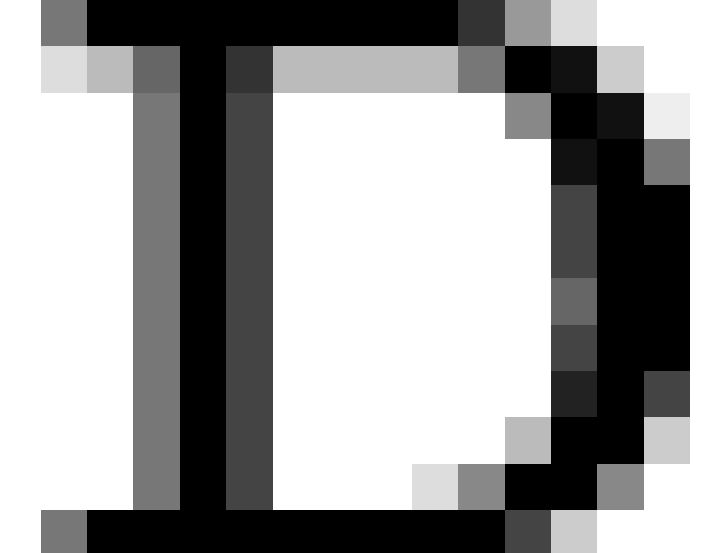 matrix, combined GSS data
matrix, combined GSS data
| |
GOD |
GOCHURCH |
BELIEVE |
FOLLOW |
GOOWNWAY |
REBORN |
SAVESOUL |
a
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
| b |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
| c |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
| d |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
| e |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
| f |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
| g |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
| h |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
| i |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| j |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
| k |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| l |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| m |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
| n |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
| |
READWORD |
DOUBTS1 |
DOUBTS2 |
FAITH1 |
FAITH2 |
FRNDCON |
|
| a |
1 |
0 |
0 |
1 |
1 |
1 |
|
| b |
1 |
0 |
0 |
1 |
1 |
1 |
|
| c |
1 |
1 |
1 |
1 |
0 |
1 |
|
| d |
1 |
1 |
1 |
0 |
0 |
1 |
|
| e |
1 |
1 |
1 |
0 |
0 |
1 |
|
| f |
1 |
1 |
1 |
0 |
0 |
1 |
|
| g |
0 |
1 |
1 |
0 |
0 |
1 |
|
| h |
0 |
0 |
0 |
0 |
0 |
1 |
|
| i |
0 |
0 |
0 |
0 |
0 |
1 |
|
| j |
0 |
1 |
1 |
0 |
0 |
0 |
|
| k |
0 |
1 |
1 |
0 |
0 |
0 |
|
| l |
0 |
0 |
1 |
0 |
0 |
0 |
|
| m |
0 |
0 |
0 |
0 |
0 |
0 |
|
| m |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
One of the first questions we might ask about both the memotype and
phenotype structures is that of whether we can identify patterns of
similarity and dissimilarity among the various elements. Consider, for
instance, the set of behavioral characters. A natural measure of
dissimilarity between observed characters is the Hamming distance (19) between the respective columns of 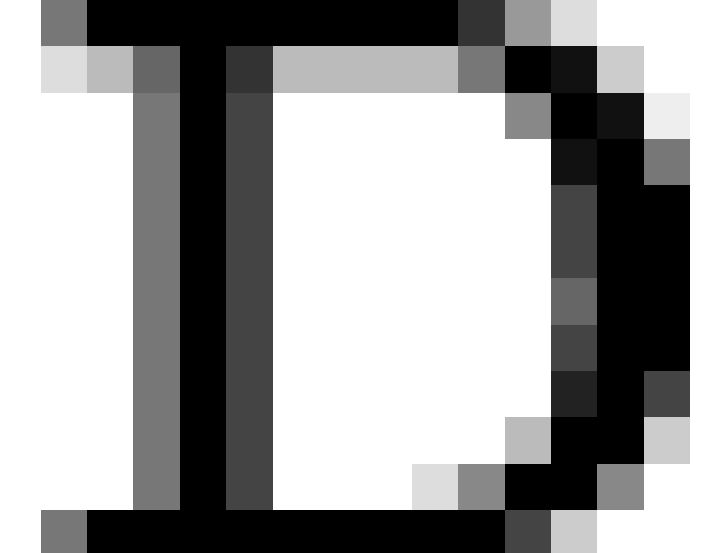 ; that is, the number of differing dependencies between the
columns. Under such a measure, a distance of zero would reflect
absolutely identical patterns of dependencies - both characters would
depend upon precisely the same memes [note 13] By turns, a large Hamming distance
would indicate that the two characters "load" on very different memes,
thus suggesting substantive dissimilarity. Interestingly, the duality of
the
; that is, the number of differing dependencies between the
columns. Under such a measure, a distance of zero would reflect
absolutely identical patterns of dependencies - both characters would
depend upon precisely the same memes [note 13] By turns, a large Hamming distance
would indicate that the two characters "load" on very different memes,
thus suggesting substantive dissimilarity. Interestingly, the duality of
the 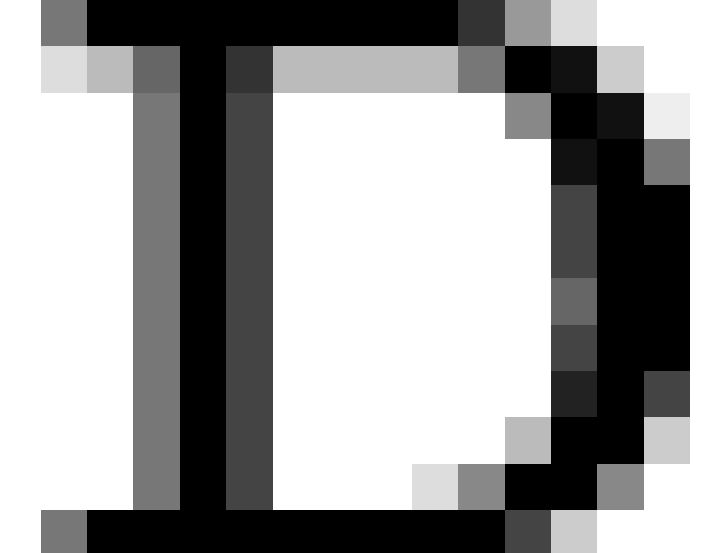 matrix implies that we can apply a similar logic to the
memes. In the latter case, we take Hamming distances between the rows
of
matrix implies that we can apply a similar logic to the
memes. In the latter case, we take Hamming distances between the rows
of 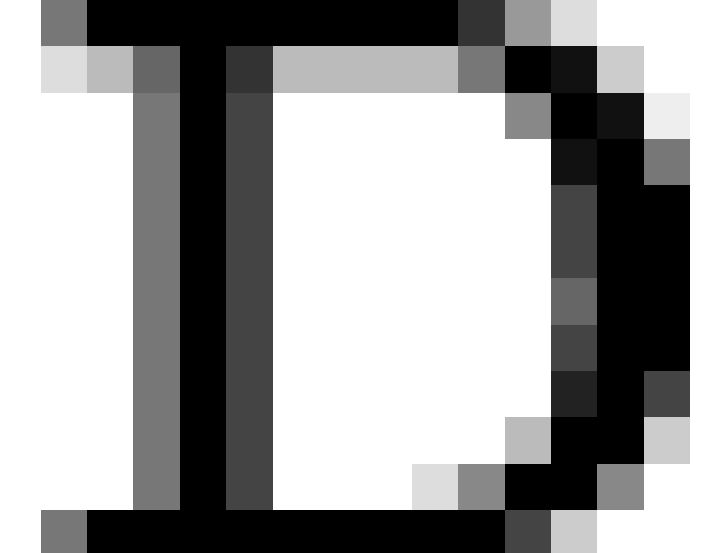 , thereby measuring the extent to which various memes share
similar patterns of connection to the character set.
, thereby measuring the extent to which various memes share
similar patterns of connection to the character set.
Given these matrices of Hamming distances, we can attempt to
represent the pattern of similarities/dissimilarities via multidimensional
scaling (MDS) (34). Two-dimensional MDS solutions for the memes and behavioral characters
are shown in Figure 3; note that the Euclidean
distances between elements in the MDS
solution approximate the underlying Hamming distances, and therefore
elements which are close together are generally more similar than those
which are far apart. Thus, we see that the the characters DOUBTS1 and DOUBTS2, while
closely related to each other, differ substantially from the other
characters. Furthermore, a "chain" of elements leads from FAITH2 to SAVESOUL,
suggesting an underlying linear similarity pattern. Substantively, this
pattern seems loosely associated with increasing Christian religiosity,
moving from a reported strengthening of faith from the birth of a child
at the one extreme to reported conversion attempts at the other. Two
associated characters - FOLLOW and GOCHURCH -
are juxtaposed, owing to the fact that they have identical memetic
dependencies. In contrast, GOOWNWAY is
isolated from all of the other memes in the set, suggesting that it has
relatively little relation to the rest of the items.
Figure 3: MDS
of latent meme-like structures (right panel) and behavioral characters
(left panel) by Hamming distance between association patterns, combined GSS data; note that FOLLOW and GOCHURCH are
superimposed (see text) (PDF
Version)
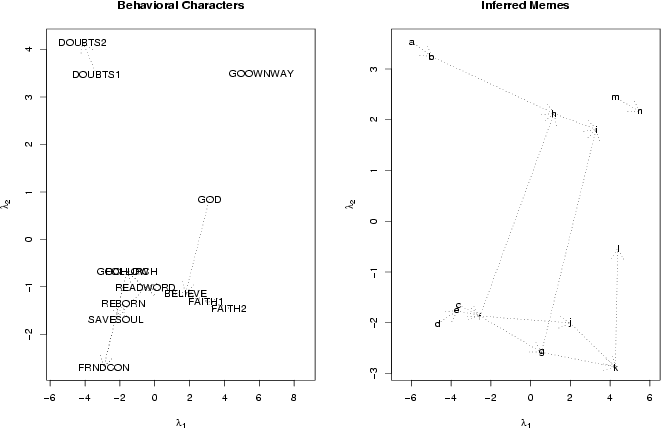 |
Turning to the putative memes, we observe four loose clusters and
one intermediate point (l). c and e are the most
closely related memes, both being similar to d and f. a and b are closely
related to each other, but relatively distant from the other clusters
which are present. Interpretation of these patterns is also aided by the
dotted arrows connecting various memes within the set. These arrows
indicate precedence, such that x precedes y if and only if
any character which depends on y also depends on x. [note 14] Interestingly,
we can see here that precedence is only loosely related to similarity:
many memes share a precedence relation with other memes which have very
different patterns of dependency. This is in strong contrast to
precedence among the characters, which follows similarity quite closely.
A better view of the precedence relations may be had by turning to
Figure 4, which shows the set of
memes, partially ordered by minimal precedence. (Such sets are referred
to as "posets.") As the figure makes clear, the structure of dependency
among memes is quite intricate. Given the complexity of the precedence
graph, it is useful to consider the interpretation of various common
structural features; one list of such features (and their
interpretations) is given in Table 6.
With this in mind, we can immediately see that the meme poset has two
components, indicating that the "miniature" Guttman scale formed by m and n has no strict
precedence relation with any other memes in the set. Turning to the
larger component, a large number of intersecting scale-like elements can
be seen, having unique origins in memes a, c, and d. The chief
enabling element within the poset is clearly f, which serves
as the critical linchpin for three memes and numerous chains. f also acts to
join the chain de
with c, a linking role which is
similar to that played by meme h (which joins f with the ab chain). The
terminal nodes for the chains of the main component are i and l, which are
thus the memes lying at the most extreme ends of their associated
scales. As we shall see, this is reflected in their phenotypic
associations.
Table 6: Behavioral
interpretations of common precedence graph features
| Graph Feature |
Interpretation |
| Vertex |
Belief |
| Edge |
Minimal precedence |
| Path |
Embedded "Guttman-like" scale |
| Component |
Maximal set of related beliefs |
| In-isolate |
"Elementary" belief with no dependencies |
| Out-isolate |
"Terminal" belief on which nothing depends |
| In-star |
Belief with multiple distinct dependencies |
| Out-star |
Belief which "enables" multiple beliefs |
|
Returning to the behavioral characters, we can use the same logic to
identify and interpret precedence based on memetic dependencies. A plot
of the relevant poset is provided in Figure 5.
The graph structure shown in Figure 5
displays a striking pattern of what appear to be interlocking but
partially distinct religiosity scales. The critical nexus for the
behavioral characters seems to be READWORD,
which depends on a number of more basic religion/spirituality characters
and which in turn appears to act as an enabler for more high-commitment
Christian beliefs. These last characters, in turn, seem to be split into
two chains, one stressing individual experiences (SAVESOUL and REBORN) and
the other emphasizing attention to collective activities (GOCHURCH/FOLLOW and FRNDCON). REBORN and FRNDCON, then,
would seem to reflect the extremes of the individual experience and
collective involvement Christian belief scales (respectively).
Interestingly, reporting that one has never had religious doubts due to
personal suffering or "evil in the world" does not have a strict
precedence interaction with other characters, and GOOWNWAY seems
to be entirely distinct. It seems particularly noteworthy that the line
of demarcation here is not associated with the type of character
in question: the main component contains a tightly integrated mix of
personal experience, normative judgment, and pure belief items. Rather,
it would seem that the distinction between components is based either on
the direction of the belief (positive/negative) or on some other latent
structural factor. As we shall see, there is evidence for the latter
interpretation.
So far, we have focused exclusively on structure within meme
and character sets; much of our interest, however, lies on the
relationship between the two. Here, as before, our guide is the  matrix, which provides an explicit accounting of the
macro/micro dependencies within the data set. While a good deal can be
learned from direct perusal of
matrix, which provides an explicit accounting of the
macro/micro dependencies within the data set. While a good deal can be
learned from direct perusal of  , it is also helpful to examine the graph formed by one or
more posets together with the cross-type dependencies. Such a graph is
shown in Figure 6, which combines the
meme poset with the associated characters. Following the minimalist
logic employed elsewhere, cross-type dependencies are shown minimally:
if character
, it is also helpful to examine the graph formed by one or
more posets together with the cross-type dependencies. Such a graph is
shown in Figure 6, which combines the
meme poset with the associated characters. Following the minimalist
logic employed elsewhere, cross-type dependencies are shown minimally:
if character  depends upon memes
depends upon memes  and
and  , and if
, and if  , then only
, then only 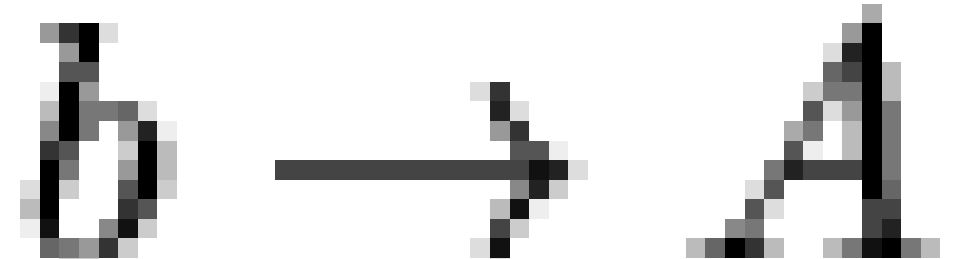 is displayed. This visualization allows one
to use a "path tracing" approach to interpreting the dependency
structure; by starting with one or more elementary memes and following
the outgoing paths, one can observe at what points one "picks up"
various behavioral characters. The figure also makes evident certain
non-obvious relationships between meme and character structures which
are of clear substantive import. Consider, for instance, REBORN and GOOWNWAY.
Considering only the MDS
solution or within-set precedence orderings, these two characters could
not seem more dissimilar: while REBORN is at
the extreme end of what appears to be a Christian religiosity scale, GOOWNWAY seems
eponymously distant from all of these characters. Yet, as Figure 6 reveals, REBORN and GOOWNWAY are
linked by their joint dependence on the
is displayed. This visualization allows one
to use a "path tracing" approach to interpreting the dependency
structure; by starting with one or more elementary memes and following
the outgoing paths, one can observe at what points one "picks up"
various behavioral characters. The figure also makes evident certain
non-obvious relationships between meme and character structures which
are of clear substantive import. Consider, for instance, REBORN and GOOWNWAY.
Considering only the MDS
solution or within-set precedence orderings, these two characters could
not seem more dissimilar: while REBORN is at
the extreme end of what appears to be a Christian religiosity scale, GOOWNWAY seems
eponymously distant from all of these characters. Yet, as Figure 6 reveals, REBORN and GOOWNWAY are
linked by their joint dependence on the 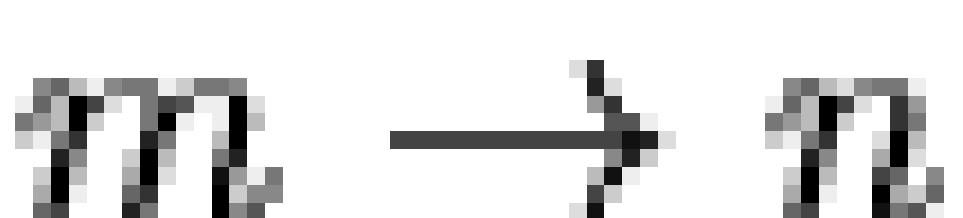 scale! Similarly, DOUBTS1 and DOUBTS2 share
a number of dependencies with FOLLOW/GOCHURCH, SAVESOUL, REBORN, FAITH1, GOD, and BELIEVE, a
fact which is not obvious from the within-type posets.
scale! Similarly, DOUBTS1 and DOUBTS2 share
a number of dependencies with FOLLOW/GOCHURCH, SAVESOUL, REBORN, FAITH1, GOD, and BELIEVE, a
fact which is not obvious from the within-type posets.
Figure 6: Character
dependencies with inferred meme poset, combined GSS
data (PDF
Version)
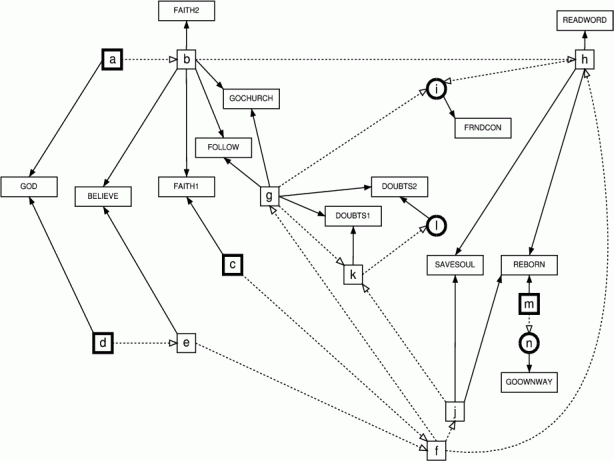 |
Putting all of this together, we can discern much regarding the
latent structure of American religious belief in the period from
1988-1998. First, there is a clear structure of increasing commitment to
Christian religiosity which begins with the acceptance of a personal god
and an experience of having one's religious faith strengthened by events
such as the birth of a child, leads through periodic Bible reading in
the home, and then divides into two high-commitment scales. One of these
involves reports of individual experiences and activities usually
identified with evangelical protestantism, including personal attempts
at conversion of others and the experience of being "born again." The
other involves normative judgments and experiences which are more
collective in nature, including a belief in the importance of church
attendance and obedience to church authority, and reporting having a
friend who is a member of one's congregation. A deep structural linkage
exists between belief in the importance of following one's conscience
even when it conflicts with religious authorities and reporting a born
again experience, despite the many differences in dependencies between
the two. The inferred memes associated with this linkage may be
interpreted as reflecting a Guttman scale for belief in the importance
of personal religious experiences, with m constituting
the belief that such experiences constitute valid religious knowledge,
and n
constituting the more extreme notion that one's personal experience or
gnosis is more reliable than the teachings of religious authorities.
(See Table 7 for one set of possible
interpretations of the meme system.) Similarly, reporting that one has
never had religious doubts due to personal suffering or "evil in the
world" appears to depend on a mixture of Guttman scales involving
religious conviction, with precursors g (apparently
reflecting confidence in the authority of the church) and j (reflecting an
immunity to doubt based on the opinions of others) culminating first in
an immunity of conviction to others' actions (k) and finally
in an immunity of conviction to one's own suffering (l). Belief in
the importance of church attendance and the obedience to religious
authority appears to follow from a combination of a belief in the
potential of religion to bring positive benefits, combined with a
conviction in the reliability of religious institutions. A similar
crossover between the immunity of doubt to others' opinions and the
efficacy of the Bible would seem to lie behind self-reported conversion
activity. Other crossovers between general religious conviction and
belief in the personal, positive benefits of religion appear to be
underlie articulated belief in a personal god, the notion that such
belief is an important part of being a good Christian or Jew, and the
report that one's religious faith has been strengthened by various
personal events. Thus, by examining the latent algebraic structure of
American religious belief, we are able not only to discern direct
relationships among manifest behavioral characters, but also more subtle
connections based on presumptive memetic dependencies.
Table 7: Possible interpretations of
inferred meme-like structures, combined GSS data
| Meme |
Possible Interpretation |
| a |
Religion/spirituality has personal
significance |
| b |
Religion/spirituality brings positive
benefits |
| c |
Religion/spirituality reduces suffering in
times of trouble |
| d |
There is a god |
| e |
One must be confident that there is a god |
| f |
Belief in god is an important bulwark
against adversity |
| g |
One must have confidence in religious
institutions |
| h |
The Bible should be consulted regularly |
| i |
One must associate with co-religionists |
| j |
One should counter doubt regarding one's
religious beliefs |
| k |
One's religious conviction should not be
affected by others' actions |
| l |
One's religious conviction should not be
affected by one's experiences |
| m |
Personal religious experiences are a valid
source of knowledge (gnosis) |
| n |
Personal religious experiences outweigh
religious authority |
|
As a final note, we reiterate the observation that our
interpretation of the potential memetic structure uncovered is limited
to its association with the observed behavioral phenotypes. These, in
turn, are limited by the available character set. Thus, as noted
earlier, we cannot discern fine-grained distinctions among those not
carrying any of the four "root" memes (a, c, d, and m), because (by
construction) the absence of these memes corresponds to a phenotype
which evidences none of the characters under study. [note 15] Broadening the
character set (e.g., to encompass subtle distinctions among varieties of
atheism or agnosticism) would presumably result in the discovery of
additional candidate memes associated with the new characters; some of
these would likely be root memes, while others may have varying degrees
of dependency on novel or extant candidate memes. It is thus important
to bear in mind that the candidate set identified here is not exhaustive
of the religious domain.
3 From
Cross-Sectional Analysis to Diffusion
The basic strategy followed here might be described (with apologies
to Firth (10)) by the notion that "you
shall know a meme by the company it keeps." As opposed to inspecting
longitudinal data for patterns of persistence which might imply an
underlying diffusion process, we instead seek indirect evidence of
latent discrete structures in the distribution of behavioral characters.
This latter strategy has the tremendous advantage of leveraging existing
data resources (which are overwhelmingly cross-sectional), but at some
point it is critical to determine which (if any) of the latent meme-like
structures inferred by the method are truly transmissible. Although a
detailed treatment of this topic is beyond the scope of this paper, we
here make some suggestions which may be of use for subsequent work in
this area.
An important implication of meme theory which sets it apart from
many other diffusion models (e.g. 12,21,3,4) is that uniform diffusion on the level
of the memotype can give rise to non-uniform change at the level of the
phenotype. By way of illustration, consider the expression mechanism of
Table 5. If an individual (A) exhibiting the
character SAVESOULinteracts
with an individual (B) exhibiting the character GOOWNWAY,
standard diffusion models would generally predict some chance that each
would adopt the others' behavioral state, i.e., that the A would gain GOOWNWAY or
drop SAVESOUL,
or that B would gain SAVESOUL or
drop GOOWNWAY.
Assuming that diffusion occurs at the memetic level, however,
Table 5 would suggest the possibility that
one or both individuals might exhibit the character REBORN; this
follows from the fact that A must hold memes a-f, h, and j, B must hold
memes m and n, and the union
of these sets covers REBORN. Such a
prediction would not arise from any of the classical diffusion models
cited above (but see the evolutionary learning models of 9,30). Given
this, one strategy for testing hypothesized memetic structures would be
to identify novel phenotypic consequences from memetic crossovers (using
the  matrix), place individuals with the appropriate preconditions
in contact with one another, and compare the individuals' post-encounter
phenotypes with the predictions of the theory. Since these tests would
focus on effects related to specific characters, reasonable power could
be obtained with fairly small samples - this ability to screen
populations for easily evaluated phenotypic effects is another benefit
of the cross-sectional modeling strategy.
matrix), place individuals with the appropriate preconditions
in contact with one another, and compare the individuals' post-encounter
phenotypes with the predictions of the theory. Since these tests would
focus on effects related to specific characters, reasonable power could
be obtained with fairly small samples - this ability to screen
populations for easily evaluated phenotypic effects is another benefit
of the cross-sectional modeling strategy.
Beyond testing novel phenotypic predictions for specific characters,
the model of Equation 1 could also be
used as the starting point for a more general diffusion model, the
predictions of which could be compared with intertemporal data. In
particular, it is noteworthy that one trivial consequence of the
conjunctive memetic model employed here is that behavioral phenotypic
change - if motivated by change at the memetic level - should take the
form of a walk on the phenotype lattice. Placing a probability
distribution on the rate of meme transfer would yield a matrix of
transition probabilities between lattice states. This, in turn, could
easily be used to predict such things as first passage times for various
phenotypic states, predictions which could be compared with data arising
from experimental or other sources. Here, as before, it is important to
emphasize the fact that the initial cross-sectional study dramatically
reduces the number of states which must be considered for the transition
matrix, and provides reasonable initial clues as to the possible
transition probabilities. This "rough cut" of the meme system can thus
serve to greatly improve the efficiency of subsequent inference based on
intertemporal data.
Examination of data from the 1988 and 1998 GSS
religion modules using Martin and Wiley's latent algebraic approach (27,28) reveals a
complex structure of discrete latent constructs beneath the surface of
the question responses. Meme theory suggests the possibility that these
inferred constructs are actually memes, in which case the posets
shown here provide a plausible model of the paths by which particular
religious memes may come to "infect" a given host (7). While longitudinal data will be
required to determine whether these inferred constructs meet the
transmissibility criterion, the general approach shown here should be a
useful preliminary step in future memetic studies of religion
(particularly where more diverse sets of characters may be considered).
Combined with studies on the evolution of religious characters across
time (e.g., 24,16) inference of
latent structure from large, cross-sectional studies such as the GSS
may greatly improve the prospects for a memetic theory of religious
belief.
1. S. Blackmore. The
Meme Machine. Oxford University Press, Oxford, 1999.
2. H. Bozdogan. Akaike's
Information Criterion and recent developments in information complexity. Journal
of Mathematical Psychology, 44:61-91,
2000.
3. C. T. Butts. A bayesian
model of panic in belief. Computational and Mathematical
Organization Theory, 4(4):373-404,
1998.
4. K. M. Carley. A theory
of group stability. American Sociological Review, 56(3):331-354, 1991.
5. J. A. Davis and
T. W. Smith. General Social Survey, 1988. National
Opinion Research Center, Chicago, 1988.
6. J. A. Davis,
T. W. Smith, and P. V. Marsden. General Social Survey,
1998. National Opinion Research Center, Chicago, 1998.
7. R. Dawkins. Viruses of
the mind. In B. Dahlbohm, editor, Dennett and His Critics:
Demystifying Mind, pages 13-27. Blackwell, Oxford, 1993.
8. M. de Jong. Survival of
the institutionally fittest concepts. Journal of Memetics -
Evolutionary Models of Information Transmission, 3, 1999. http://cfpm.org/jom-emit/1999/vol3/de_jong_m.html
9. T. J. Fararo and
C. T. Butts. Advances in Generative Structuralism: Structured
agency and multilevel dynamics. Journal of Mathematical Sociology,24(1):1-65, 1999.
10. J. R. Firth. Papers
in Linguistics, 1934-1951. Oxford University Press, London, 1957.
11. F. Flentge,
D. Polani, and T. Uthmann. Modelling the emergence of
possession norms using memes. Journal of Artificial Societies and
Social Simulation, 4(4),
2001. http://jasss.soc.surrey.ac.uk/4/4/3.html
12. N. Friedkin
and E. C. Johnsen. Social influence and opinions. Journal of
Mathematical Sociology, 15:193-206,
1990.
13. D. Gatherer.
Identifying cases of social contagion using memetic isolation:
Comparison of the dynamics of a multisociety simulation with an
ethnographic data set. Journal of Artificial Societies and Social
Simulation, 5(4), 2002. http://jasss.soc.surrey.ac.uk/5/4/5.html
14. L. A. Goodman.
Exploratory latent structure analysis using both identifiable and
unidentifiable models. Biometrika, 61(2):215-231, 1974.
15. L. A. Goodman. New
methods for analyzing the intrinsic character of qualitative variables
using cross-classified data. American Journal of Sociology, 93(3):529-583, 1987.
16. J. D. Gottsch.
Mutation, selection, and vertical transmission of theistic memes in
religious canons. Journal of Memetics - Evolutionary Models of
Information Transmission, 5,
2001. http://cfpm.org/jom-emit/2001/vol5/gottsch_jd.html
17. L. Guttman. The basis
for scalogram analysis. In S. A. Stouffer, L. Guttman,
E. A. Suchman, P. F. Lazarsfeld, S. A. Star, and
J. A. Clausen, editors, Measurement and Prediction, Studies of
Social Psychology in World War II, volume 4. Princeton
University Press, Princeton, NJ, 1950.
18. E. H. Haertel
and D. E. Wiley. Representations of ability structures:
Implications for testing. In N. Frederiksen, R. Mislevy, and
I. Bejar, editors, Test Theory for a New Generation of Tests,
pages 359-384. Erlbaum, Hillsdale, NJ, 1993.
19. H. Hamming. Error
detecting and error correcting codes. Bell System Technical Journal, 29:147-160, 1950.
20. D. L. Hull. Taking
memetics seriously: Memetics will be what we make it. In R. Aunger,
editor, Darwinizing Culture: The Status of Memetics as a Science.
Oxford University Press, Oxford, 2000.
21. D. Krackhardt.
Organizational viscosity and the diffusion of controversial innovations. Journal
of Mathematical Sociology, 22(2):177-199,
1997.
22. B. Latané,
A. Nowak, and J. H. Liu. Measuring emergent social phenomena:
Dynamism, polarization, and clustering as order parameters of social
systems. Behavioral Science, 39:1-24,
1994.
23. P. F.
Lazarsfeld and N. W. Henry. Latent Structure Analysis.
Houghton-Mifflin, New York, 1968.
24. A. Lord and
I. Price. Reconstruction of organisational phylogeny from memetic
similarity analysis: Proof of feasibility. Journal of Memetics -
Evolutionary Models of Information Transmission, 5, 2001. http://cfpm.org/jom-emit/2001/vol5/lord_a&price_i.html
25. B. Markovsky
and S. Thye. Social influences on paranormal beliefs. Sociological
Perspectives, 44(1):21-44,
2001.
26. J. L. Martin. Power,
authority, and the constraint of belief systems. American Journal
of Sociology, 107(4):861-904,
2002.
27. J. A. Wiley and J. L.
Martin. Algebraic representations of beliefs and attitudes: Partial
order models for item responses. Sociological Methodology, 29:113-146, 1999.
28. J. L. Martin and
J. A. Wiley. Algebraic representations of beliefs and attitudes II:
Microbelief models for belief data. Sociological Methodology, 30:123-164, 2000.
29. A. L. McCutcheon. Latent
Class Analysis, volume 64 of Quantitative Applications
in the Social Sciences. Sage, Newbury Park, 1987.
30. J. H. Miller,
C. T. Butts, and D. C. Rode. Communication and cooperation. Journal
of Economic Behavior and Organization, 46(4), 2001.
31. M. Ridley. Evolution.
Blackwell Scientific Publications, Boston, 1993.
32. A. K. Romney. Systemic
culture patterns as basic units of cultural transmission and evolution. Cross-Cultural
Research, 35(2):154-178,
2001.
33. N. Rose. Controversies in
meme theory. Journal of Memetics - Evolutionary Models of
Information Transmission, 2,
1998. http://cfpm.org/jom-emit/1998/vol2/rose_n.html
34. W. S. Torgerson.
Multidimensional scaling: I, theory and method. Psychometrika,
17:401-419, 1952.
35. W. S. Torgerson. Theory
and Method of Scaling. Wiley, New York, 1962.
36. L. Wasserman.
Bayesian model selection and model averaging. Journal of
Mathematical Psychology, 44:92-107,
2000.
37. J. S. Wilkins. What's
in a meme? reflections from the perspective of the history and
philosophy of evolutionary biology. Journal of Memetics -
Evolutionary Models of Information Transmission, 2, 1998. http://cfpm.org/jom-emit/1998/vol2/wilkins_js.html
Acknowledgements
The authors would like to thank John Levi Martin, Philip Cohen, and
Kim Romney for their helpful comments regarding this work.
Notes
1. Full
address: Department of Sociology and Institute for Mathematical
Behavioral Sciences; University of California, Irvine; Irvine, CA 92697;
Tel: +1 (949) 824-8591
2. A lattice is a partially ordered
set for which all finite subsets have a least upper bound and a greatest
lower bound. In the limited context considered here, a lattice can be
thought of as a collection of binary vectors which are closed under
elementwise intersection (e.g., indicators for a set of features which
may or may not be present). See the appendix of Martin and Wiley (28) for an
application-centered elaboration.
3. It is possible to generalize the
sampling assumptions, but we shall restrict ourselves to the simple case
for the present.
4. I.e., is the binary vector
whose ith
position equals 1 iff
is the binary vector
whose ith
position equals 1 iff 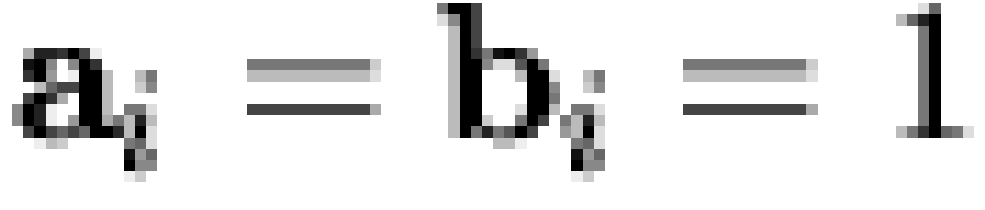 .
.
5. Although the differing framework of Markovsky and Thye (25) does not
allow us to assess whether this transference involved microbeliefs in
the sense used here, it is interesting to note that the indirect
measures used in their experiments (subjective assessments of an object
which had purportedly been exposed to "pyramid power") would seem a
priori likely to have tapped latent belief change of some sort.
6. Draws were subsampled from a Markov
Chain Monte Carlo simulation of length 2,500,000, every 500th step being
accepted.
7.I.e.,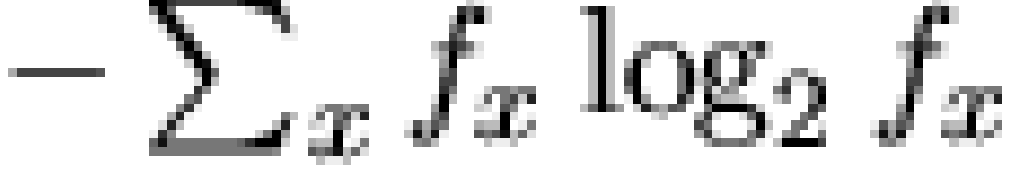 , where
, where  is the empirical frequency of
phenotype
is the empirical frequency of
phenotype  .
.
8. Akaike's Information
Criterion (AIC) and the Bayesian Information
Criterion (BIC) are generalized fit indices which can be used to compare
non-nested models. Both criteria are based on tradeoffs between fit to
the data at hand (i.e., likelihood of the data under the proposed model)
and parsimony (e.g., the expected decrease in predictive accuracy due to
overfitting); the two differ in the precise assumptions involved. An
excellent overview of the AIC (and related information-theoretic
criteria) can be found in Bozdogan (2),
with a similar introduction to Bayesian model selection techniques in Wasserman (36).
9. Approximately 29 elements would be
expected to have non-negligible class probabilities if closure had no
relationship to the distribution of phenotypes.
10. Note that Guttman scales are
lattices, and hence are special cases of the general lattice model.
11. These are more properly thought of
as "latent meme-like constructs," though for reasons of brevity we refer
to them here simply as memes. It is hoped that the reader will not
forget their provisional status, however!
12. In the present context, we refer to
memes as being "present" or "held" if they take allele 1, and "not held"
or "absent" if they take allele 0. Such usage should not imply that a
meme's state necessarily implies a physical presence or absence.
13. Insofar as can be inferred from the
data at hand, at least.
14. Note that the precedence relations
shown in the included figures are minimal, in the sense that  only if
only if 
 (where precedence
is signified by
(where precedence
is signified by  and where
and where  iff
iff  and
and  ).
).
15. Deviations from this prediction are
taken to arise at random with probabilities given in Table 3. Thus, some persons carrying none of
the candidate memes would be expected to report having read the Bible at
home in the past year (apx 30%, in this case), but this is still much
lower than the rate which would be expected for persons carrying all of
the identified memes (apx 83%).
© JoM-EMIT 2003
 Butts, C. T.and
Hilgeman, C. (2003). Inferring Potential Memetic Structure
from Cross-Sectional Data: An Application to American Religious Beliefs.
Butts, C. T.and
Hilgeman, C. (2003). Inferring Potential Memetic Structure
from Cross-Sectional Data: An Application to American Religious Beliefs.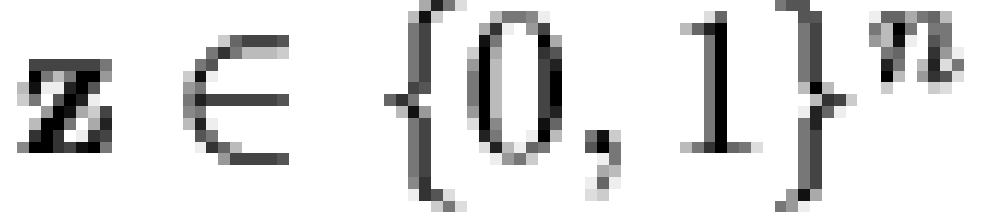 is a vector of
"microbeliefs,"
is a vector of
"microbeliefs," 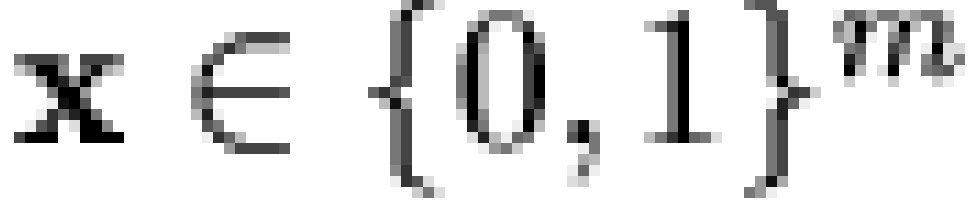 is a vector
of responses (or "macrobeliefs"), and
is a vector
of responses (or "macrobeliefs"), and  is an
is an  dichotomous dependency matrix, then it is
assumed that
dichotomous dependency matrix, then it is
assumed that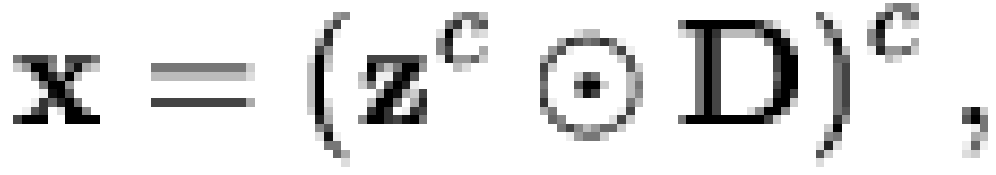
 represents the Boolean inner
product and
represents the Boolean inner
product and  is the Boolean complement
operator. Thus, a given individual is predicted to hold macrobelief
is the Boolean complement
operator. Thus, a given individual is predicted to hold macrobelief  if and only if they hold all microbeliefs
if and only if they hold all microbeliefs  such that
such that 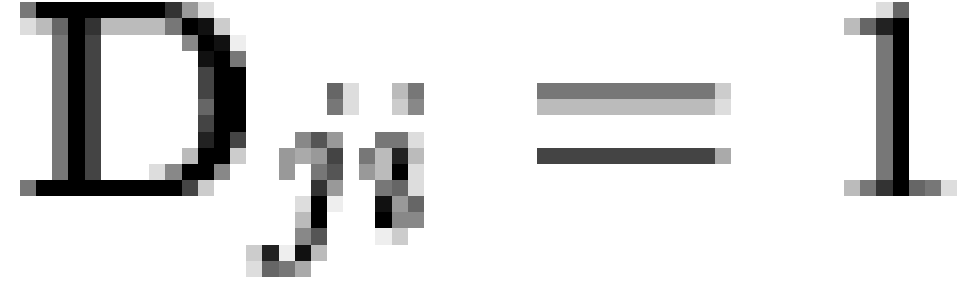 . Generally, we
also assume that the columns of
. Generally, we
also assume that the columns of  be a matrix whose rows contain all
observable macrobelief states for some
be a matrix whose rows contain all
observable macrobelief states for some  to be a
meet-irreducible element (MIRE) of
to be a
meet-irreducible element (MIRE) of 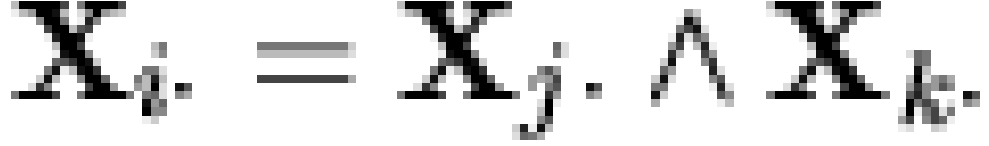 implies
implies 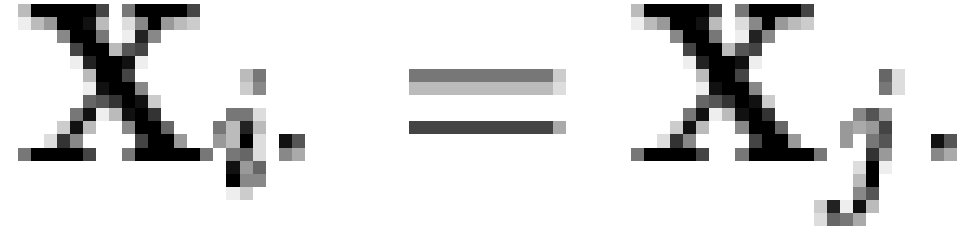 or
or 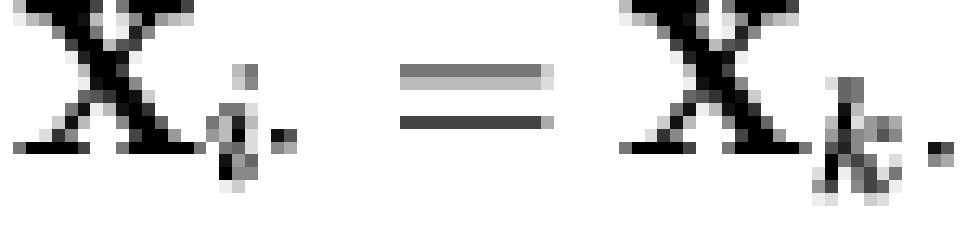 for all
for all 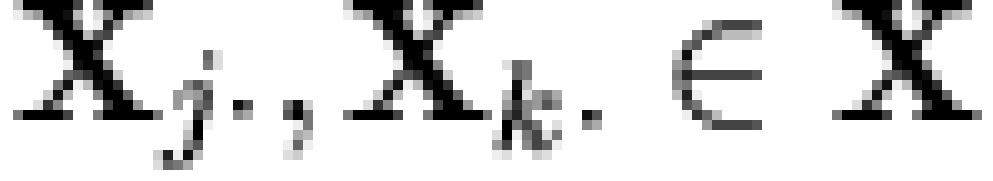 (where
(where  is the intersection operator [
is the intersection operator [ is a matrix whose rows contain the
MIREs of
is a matrix whose rows contain the
MIREs of 
 )
are treated by Wiley and Martin as arising from the true latent state (
)
are treated by Wiley and Martin as arising from the true latent state (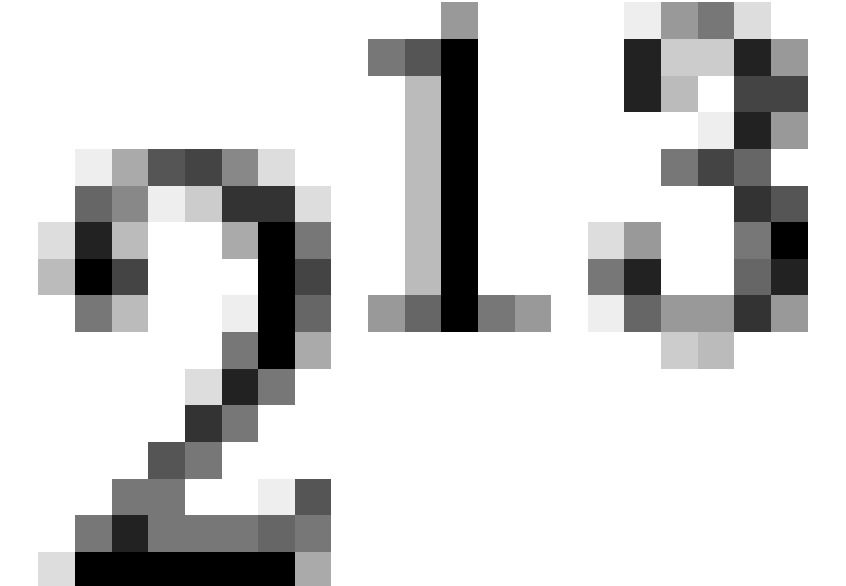 ), of
which 718, 646, and 1056 were observed for the 1988, 1998, and combined
samples (respectively). Our analysis, then, centers on the frequencies
of these behavioral phenotypes, and on their associated characters.
), of
which 718, 646, and 1056 were observed for the 1988, 1998, and combined
samples (respectively). Our analysis, then, centers on the frequencies
of these behavioral phenotypes, and on their associated characters. test of homogeneity indicated no significant
difference between the distributions (1070.039 on 8191 degrees of
freedom,
test of homogeneity indicated no significant
difference between the distributions (1070.039 on 8191 degrees of
freedom,  ). Due to the sparseness
of the sample, additional tests were performed as well. A Monte Carlo
). Due to the sparseness
of the sample, additional tests were performed as well. A Monte Carlo  conditioning on row/column marginals with 5000 replicate
draws [
conditioning on row/column marginals with 5000 replicate
draws [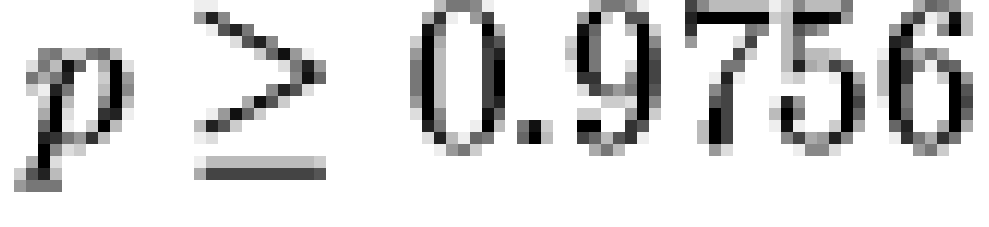 ). Taken together,
these tests suggest that any observed deviations between the 1988 and
1998 phenotype distributions are typical of what would be expected by
chance variation, and that this conclusion is quite robust to choice of
similarity measure.
). Taken together,
these tests suggest that any observed deviations between the 1988 and
1998 phenotype distributions are typical of what would be expected by
chance variation, and that this conclusion is quite robust to choice of
similarity measure. 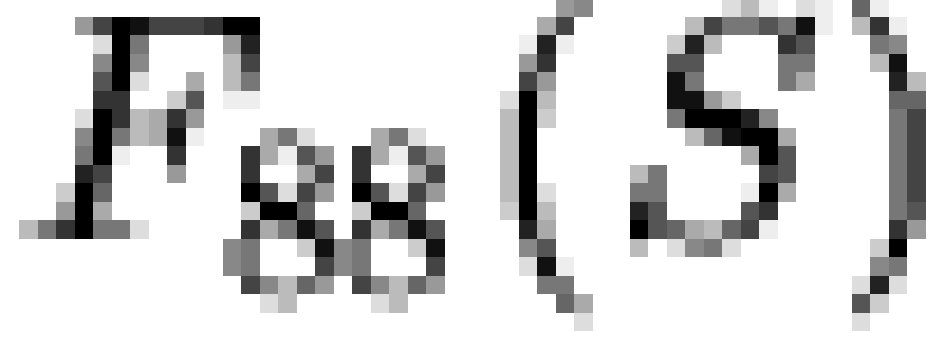 to be the fraction of
cases from the 1988 sample accounted for by pattern set
to be the fraction of
cases from the 1988 sample accounted for by pattern set 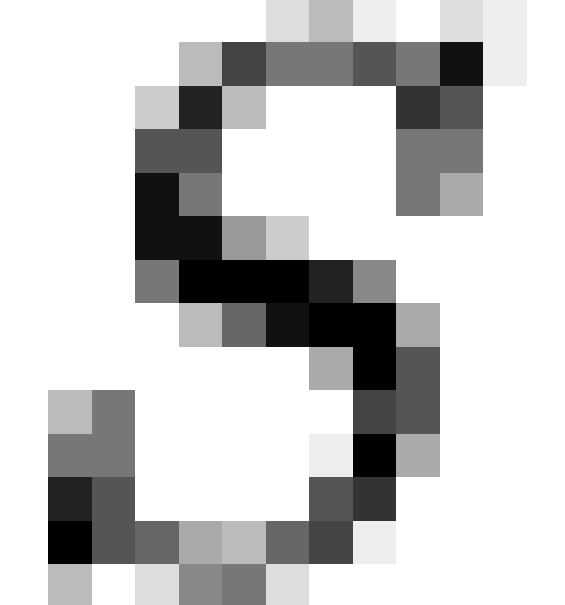 (with
(with 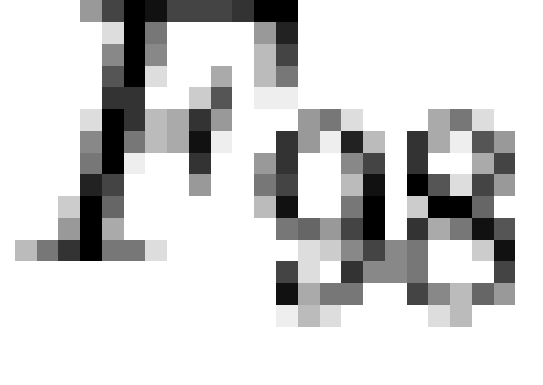 defined analogously). Next,
we define
defined analogously). Next,
we define 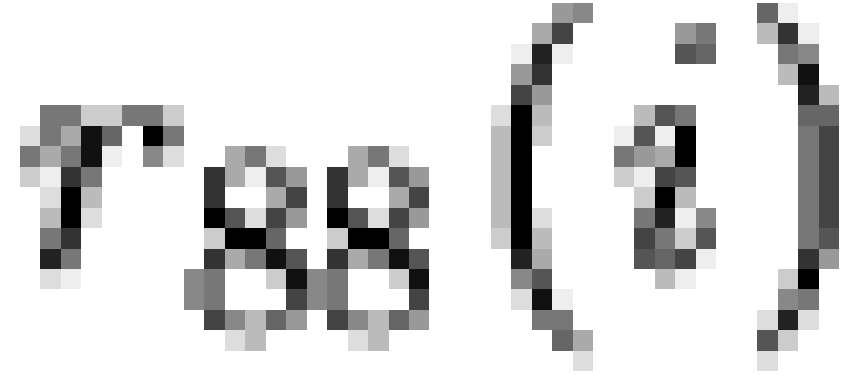 and
and  to be the set of all
patterns for the 1988 and 1998 samples (respectively) having (ascending)
sample rank less than or equal to
to be the set of all
patterns for the 1988 and 1998 samples (respectively) having (ascending)
sample rank less than or equal to  . Given this, the "coverage ratios"
. Given this, the "coverage ratios"  and
and  can be used to assess the detailed agreement of the two
distributions regarding the most frequent cases. Where the two
distributions are precisely equal, both coverage ratios are equal to 1;
as the distributions deviate from equality, the ratios will shift
correspondingly. Plots of coverage ratios for the
can be used to assess the detailed agreement of the two
distributions regarding the most frequent cases. Where the two
distributions are precisely equal, both coverage ratios are equal to 1;
as the distributions deviate from equality, the ratios will shift
correspondingly. Plots of coverage ratios for the 
 ,
, 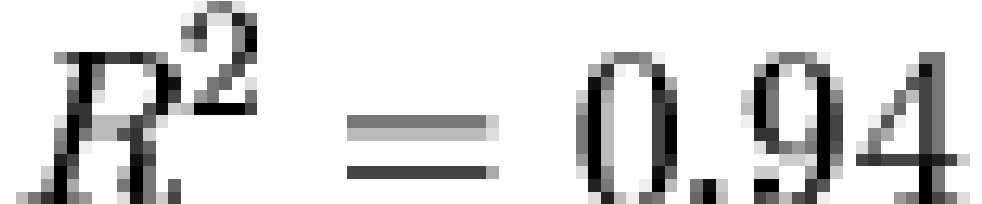 ). Although some minor deviations are
present (partially due to granularity effects), the relationship is
clearly not exponential in form (
). Although some minor deviations are
present (partially due to granularity effects), the relationship is
clearly not exponential in form (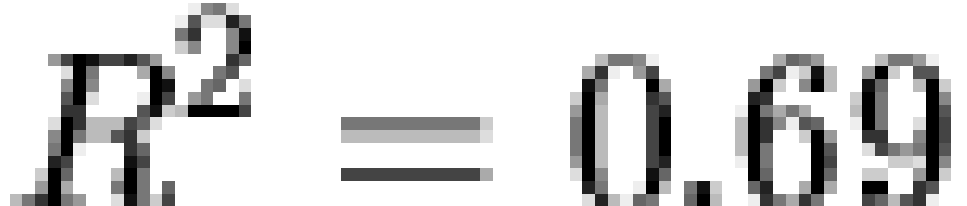 ). Thus, the overall frequency distribution
displays an extremely high degree of concentration on the most common
values, combined with a "long tail" of numerous patterns observed in
only a few instances. This should be contrasted with an equivalent
exponential model, in which less concentration would be observed on the
most common patterns, coupled with a lighter tail.
). Thus, the overall frequency distribution
displays an extremely high degree of concentration on the most common
values, combined with a "long tail" of numerous patterns observed in
only a few instances. This should be contrasted with an equivalent
exponential model, in which less concentration would be observed on the
most common patterns, coupled with a lighter tail.
 , the
, the  most frequent patterns were extracted from the
combined data set and closed under intersection to form a lattice (
most frequent patterns were extracted from the
combined data set and closed under intersection to form a lattice (  ). A confirmatory
latent class model with itemwise false positive/false negative error
parameters (
). A confirmatory
latent class model with itemwise false positive/false negative error
parameters ( was selected such that the
was selected such that the  was minimized. For
the combined
was minimized. For
the combined  state
state
 state
state


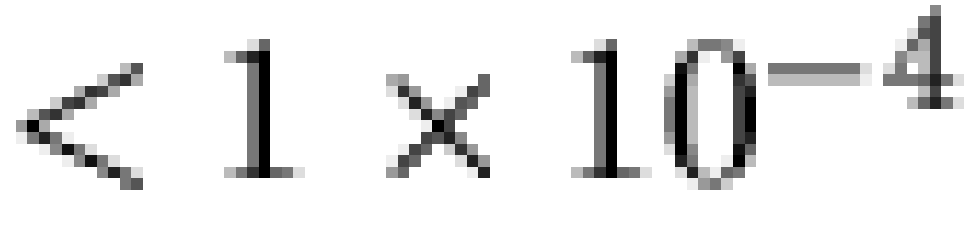
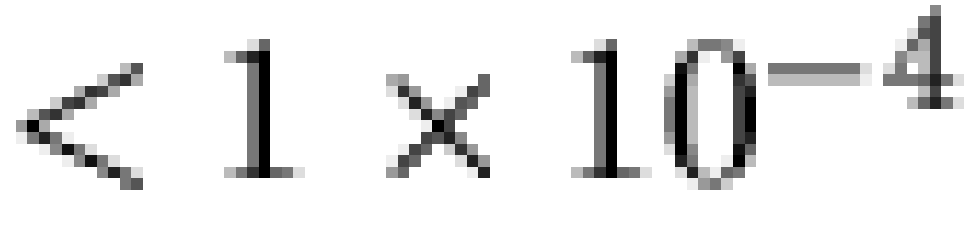
 ). Taken together, these
results indicate that: the lattice model is an acceptable representation
of the data; the unrestricted lattice is substantially superior to a
simple, unidimensional structure; and the unrestricted lattice is also
substantially superior to a null model of itemwise independence.
). Taken together, these
results indicate that: the lattice model is an acceptable representation
of the data; the unrestricted lattice is substantially superior to a
simple, unidimensional structure; and the unrestricted lattice is also
substantially superior to a null model of itemwise independence.
 )
)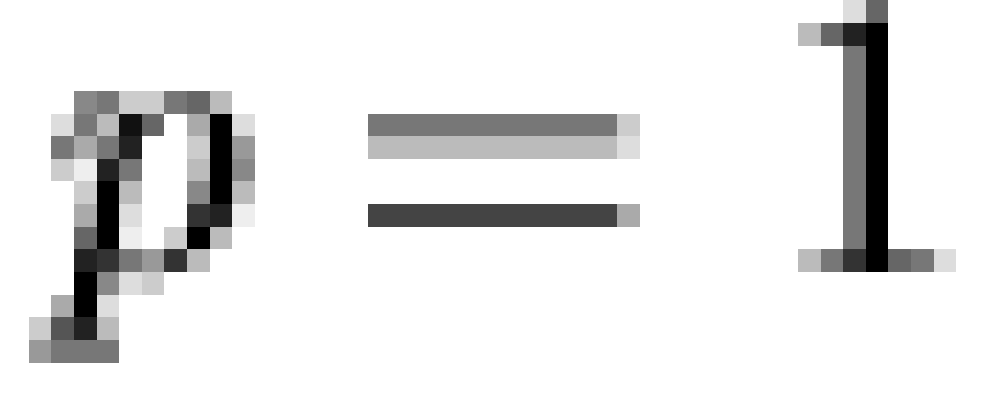 )
)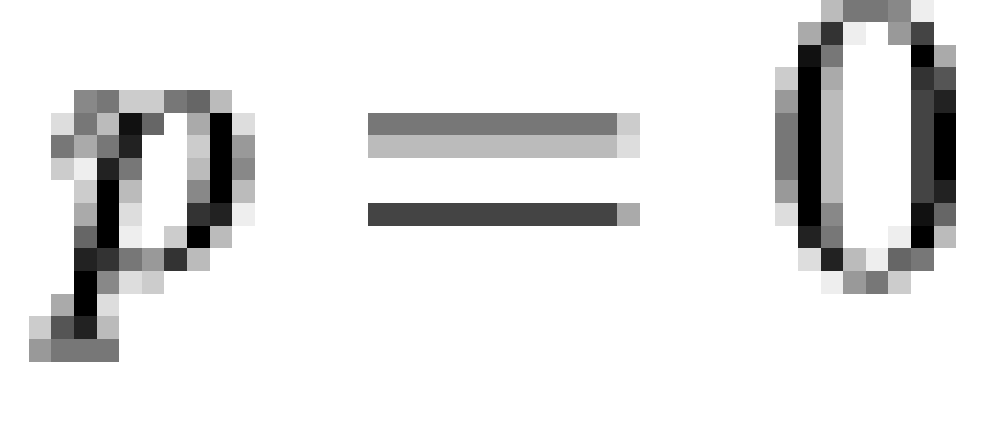 )
) matrix for the combined
matrix for the combined 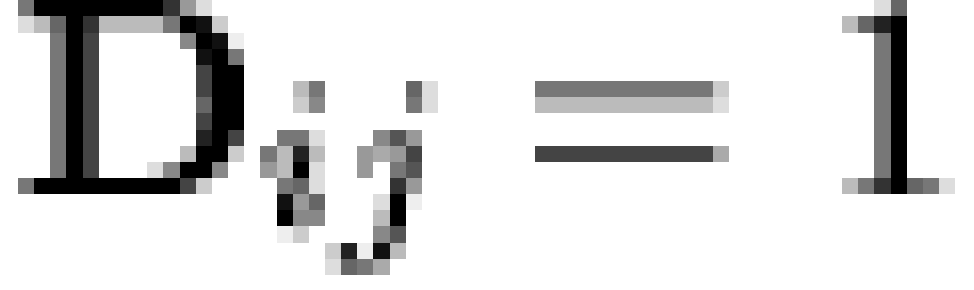 if and only if
character
if and only if
character  depends on meme
depends on meme 
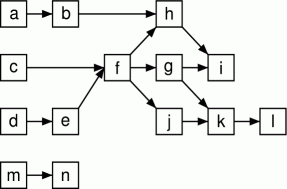
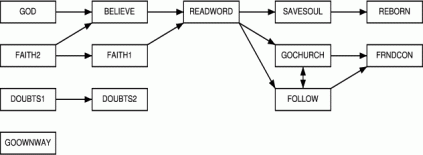
 depends upon memes
depends upon memes  and
and  , and if
, and if  , then only
, then only  is displayed. This visualization allows one
to use a "path tracing" approach to interpreting the dependency
structure; by starting with one or more elementary memes and following
the outgoing paths, one can observe at what points one "picks up"
various behavioral characters. The figure also makes evident certain
non-obvious relationships between meme and character structures which
are of clear substantive import. Consider, for instance,
is displayed. This visualization allows one
to use a "path tracing" approach to interpreting the dependency
structure; by starting with one or more elementary memes and following
the outgoing paths, one can observe at what points one "picks up"
various behavioral characters. The figure also makes evident certain
non-obvious relationships between meme and character structures which
are of clear substantive import. Consider, for instance,  scale! Similarly,
scale! Similarly, 
 is the binary vector
whose
is the binary vector
whose 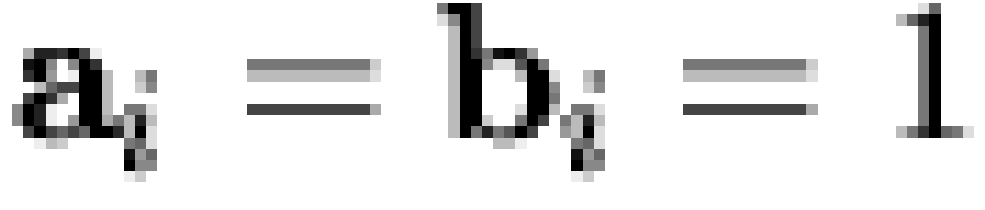 .
.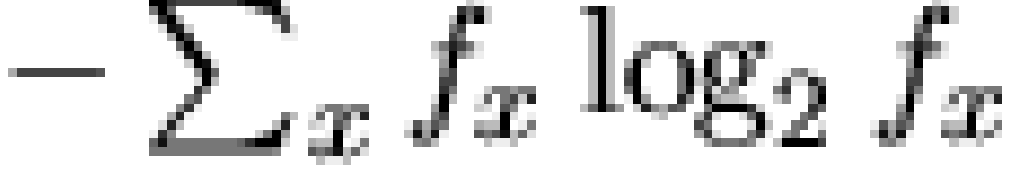 , where
, where  is the empirical frequency of
phenotype
is the empirical frequency of
phenotype  .
.  only if
only if 
 (where precedence
is signified by
(where precedence
is signified by  and where
and where  iff
iff  and
and  ).
).