Journal of Memetics - Evolutionary Models of Information Transmission, 4.
http://cfpm.org/jom-emit/2001/vol4/reynolds_r&al.html
The goal of this research is to assess the impact of Culture on decision-making behavior. Specifically we are concerned whether the emergence of human culture provided humans with an adaptive advantage over non-human primate counterparts in terms of hunter-gathering capabilities. Reynolds has proposed several mathematical models of hunter-gatherer and primate decision making based upon differences in human and primate cultural traits [1], these were labeled the cultural algorithm and vector voting models respectively.In this paper an agent-based implementation of the vector voting model using Swarm is presented. Learning takes place in the model by emulation. The performance of this model in a variety of patchwork landscapes is compared with that of a random walk model. The impact that the distribution of food resources has on the outcome is also tested using several different strategies such as equal sharing, round robin, satisfied first, neediest first, and fixed rank order. The results suggest that the vector voting model performs best when certain resource sharing strategies are used (fixed rank order, satisfied first) as opposed to others such as neediest first, and equal sharing. In the latter case it behaves equivalently to a random walk. Thus, when knowledge is not shared equally, it is not adaptive to share resources equally either.
The basic context in which these two decision-theoretic models were compared was a two-dimensional cellular space divided into R discrete sub-regions or cells each of unit area. The task facing the model groups was to compute the answers to various spatial predicates or queries about the region based upon the agents current knowledge. The models were analyzed theoretically and it was shown that the ability to form a collective intelligence through the pooling of knowledge with Cultural Algorithms had some distinct advantages over the vector voting model.
In particular, predicates such as the best direction within a region in which to forage, the direction containing the most resources, was limited by the maximum area over which each individual had knowledge. On the other hand, pooling of that knowledge theoretically allowed a group to make these decisions over the entire region.
However, even in a social system where knowledge is not directly pooled, learning can take place. For example, Tomasello and Call [2] state that there are many similarities between how humans and primates understand their social worlds. Each has its own cultural system. In an extensive survey of primate cognition studies they conclude that, "all primates live in basically that same type of social world, in which they individually recognize conspecifics and appreciate both the vertical (dominance) and horizontal (affiliative) relationships that hold between group members. They also have the ability to predict the behavior of conspecifics in many situations based upon combinations of cues and insights, and in some cases to affect the behavior of group mates via various social and communicative strategies."
They state that the basic difference between primate and human cultures is that in the latter the "inter-subjectivity of human linguistic symbols- and their perspective nature as one offshoot of this inter-subjectivity- means that linguistic symbols do not represent the world directly, in the manner of perceptual or sensory-motor representations, but rather they are used by people to induce or construe certain perceptual and conceptual situations in order to attend to them in one way rather than another".
Thus, learning in a primate social system relies heavily on emulative learning. An individual watches another perform an action and observes the state changes that result. Learning in this context is directly associated with sensory motor activities relative to objects in the environment. While humans can acquire knowledge in this way as well, they are able to support the imitative learning of concepts. With imitative learning "an individual understands others as intentional agents, like the self, that have a perspective on the world that can be followed into, directed, and shared."
The idea is that even when a group makes a decision based upon the knowledge of each individual without pooling, the physical results of that decision can be observed by everyone and learning can take place in an emulative fashion. The question of interest in this paper is what additional behaviors emerge from a group that uses the vector voting approach along with an emulative learning process. Specifically, to what extent do behaviors typically observed within a primate foraging group emerge from the use of the vector voting model? In future studies we will examine the impact that adding communication and abstraction capabilities in the form of Cultural Algorithms has on these patterns of behavior.
Here we develop an agent-based implementation of the vector voting model using the Swarm Simulation environment. In section 2 we describe the theory behind the vector voting model and the emulative learning method that serves as the basis for the primate cultural transmission here. In section 3 the Swarm implementation of the vector voting model with emulative learning is presented in detail. Next, in section 4 we describe the results of running this model in a variety of environments with a variety of social configurations. Specifically, we use our system two sets of experiments. Our first set of experiments are used to determine whether the vector voting model outperforms a baseline model which performs a simple random walk through the landscape. We also observe any generalized behavior patterns that emerge from the model group. The second set of experiments is designed to observe how differences in social interaction effect the the performance of the vector voting model. Here, we propose several different ways of distributing the collected resources including approaches based upon dominance and equal sharing. We then attempt to identify which form of distribution works best in conjunction with the vector voting model. Section 5 provides our conclusions.
The motivation for the vector model can be seen in the following quote from Kummer [3, p. 66], "In choosing the direction of their departure, hamadryas baboons have to rely on information gathered on previous trips. We do not know how or by whom these sites are explored and remembered, but we know that on different mornings different males of the troop strive in different directions. The decision is made by a long process in which most of the males in the troop participate while the rest seem unconcerned. I have already described how a hamadryas troop prepares for departure during its morning rest. The troop performs slow on-the spot movement, changing its shape like an undecided ameba. Here and there, males move a few yards away from the troop and sit down, facing in a particular direction away from the center. Pseudopods are generally formed by the younger males and their groups, until one of the older males in the center rises and struts toward one of the pseudopods. At this, the entire troop is alerted and begins to depart in the indicated direction. Detailed observation reveals that two male roles are involved in leading the hamadryas troop : the younger initiators who "propose" certain directions and the deciders who choose among the proposed directions."
One of the basic decisions that a forgaing group can make is the direction in which to forage during the day. It was shown in [4] that it was not possible for a vector voting model to always select the direction with the maximal amount of resources within a region R. However, theoretical limits aside how does the vector voting model actually perform when coupled with emulative learning, the type of learning that is frequently observed in primate cultures.
In emulative learning the observer makes a cognitive connection between what action is performed and the state changes it produces. For example, a primate can observe another rolling over a log and exposing a number of insects. That action can be viewed as producing a state change which can be stored in memory. In our model, the result of a directional decision produces a trajectory through the landscape. As a result of that path each individual has an opportunity to acquire food. In each cell that the group enters the resources there are divided among group members by various strategies such as priority or fixed order access or equal sharing of resources.
At the end of the day each individual can store a memory, not of the decision, but of the result. An individual does this by associating a visible landmark with the degree to which they were fed (satisfaction scale) the day they saw that landmark. A memory can more than one landmark attached to it and different individuals in the group can associate different landmarks with their memory. The memory made by an individual is a function of the food resources that they received that day. Each individual has a maximum number of memories that it can store and a memory is forgotten after a certain number of days (memdepth) unless it is used again.
Emulative learning using memories associated with the icons encountered relative to a groups previous decision can now be used to impact future decisions. Here, our region R has a number of landmarks (numLandmarks) which are distributed through the space. The cellular space is of size N by M and a cell can have at most one landmark assigned to it. Each day after the group decides on a direction to move based upon the memories associated with the landmarks currently visible from their location (visibility).
Each individual effectively pools the satisfaction scores for the memories associated with the visible landmarks in each of the eight direction. Here the scores are represented by a preference scale from -5 to +5 where the + direction represents satisfaction and - dissatisfaction. The direction with the highest score is the direction of choice for an individual. That choice is then weighted by their status in the group. Each member then moves in the direction of their choice and is observed by the others. The group moves in the direction which achieves the highest consensus as observed by a mediator.
Group size can change based upon the extent to which individuals are fed. Individuals who have not gotten sufficient resources over a given period die and a group is removed when all of each individuals have died. On the other hand if the group has been able to feed all of it members over a given period it can add a new individual up to a maximum group size. When it reaches that size it can fission into a second group.
The model supports a variety of food distributions, agent characteristics, and foraging behaviors. Food distributions include completely random distributions, distributions based on mathematical functions, and distributions that simulate a variable distribution based upon local conditions such as terrain, water supply, etc.
Each band member can form memories of their individual successes and failures that they can use to guide their future search for food. At the beginning of each model day, each individual evaluates these memories and selects a preferred direction of travel or vector. The members of a band are polled and the direction preferred by a majority of the members is selected according to the vector voting model given in the previous section.
The band then moves in the selected direction, collecting food as they go. At the end of the day the collected resources are distributed according to the consumption strategy used, each member evaluates how well it was fed, and associates that memory with one or more visible landmarks on the terrain. Several consumption strategies are supported here. They are fixed rank order, round-robin, equal sharing, neediest first, and satisfied first. Each will be described in more detail later.
During the execution of the model, detailed information is written to files for subsequent analysis. This information includes:
Each day, every band selects a direction of travel based on the memories of the individual members of the band. Bands can move basically in a straight line in any of 8 compass directions (N, S, E, W, NE, NW, SE, SW). The distance traveled is limited to a maximum number of squares in the landscape grid. A limit of 4 squares has been used for all trials used in this paper.
Bands move in pseudo-parallel, one square at a time, in rotation among the bands. Each band continues to move in that direction until sufficient resources are acquired to feed all band members, an object is encountered, or the maximum distance limitation (4 squares) is met. A band will alter its trajectory in order to avoid an obstacle. Here the obstacles are either static (the region boundaries) or dynamic (other bands). It is assumed here that two bands cannot occupy the same cellular space at the same time. If a band encounters an obstacle a new direction is selected, based on the same vector voting mechanism used at the beginning of the day, in order to avoid the obstacle.
At the beginning of the day, each band member reviews the memories associated with any landmarks that are currently visible and forms a weighted sum of memory scores for each possible direction of travel. Weighting is based on the interval that has elapsed since the memory was formed or reinforced and the distance to the landmark. Old memories eventually expire. The direction with the highest score becomes that individuals preferred direction of travel. The direction in which the band will travel is selected by summing up the preferred direction for each voting member. The preferred directions of all adult members are scored and the band will travel in the direction that receives the most votes. One constraint that is placed on the selected direction is that no band can reverse its direction of travel from the previous day. If the reverse direction is selected, the second choice is used. The band then travels together in the selected direction with its members collecting food as they go.
Several algorithms are implemented in order to regulate the distribution of the collected food among the members of the band as they collect food in each new cell. These distribution algorithms include round robin, equal sharing, fixed rank order, neediest first, and a satisfied first strategy. Movement for the day stops when the band has traversed the maximum number of squares or when all members of the band have consumed as much food as they can for the day. Each member of the band has a Minimum Daily Requirement for food. A provision is made in the model for an individual to consume more than one day's requirement. This permits an individual that has not been fully fed in the past to "catch up". It also permits individuals to "get ahead" so that they will survive subsequent food shortages. An individual's failure to obtain the MDR on a given day produces a cumulative deficit in nutrition. If the deficit exceeds a selected limit, the individual dies.
At the end of each day, each member of the band forms memories based on how much food they obtained during the day. These memories are associated with one or more landmarks that are visible from the location at the end of the day. Both the visibility of landmarks and the visual abilities of individuals are controlled by model parameters. Each individual selects a random direction and records the landmarks that are visible in that direction. An alternative strategy of using the nearest landmarks for all individuals failed to produce enough variability of experience to drive the voting model.
The patchwork distribution represents or attempt to emulate the attributes of a semi-arid environment. This distribution is generated by creating uniform areas of food availability around each landmark on the landscape, perhaps analogous to desert oases. This distribution is created according to the following procedure;

Figure 1. An example patchwork distribution
of resources in the model.
| Object attributes | |
| Attribute | Description and usage |
| Display Interval | Controls how often the GUI display is updated. Set to 1 for all trials. |
| Experiment Duration | Number of days that the model will run before terminating. |
| Schedule Objects | Swarm scheduling control objects |
| Display Objects | Swarm display control objects |
| Object algorithms | |
| Attribute | Description and usage |
| Create model | Create the model objects |
| Run model | Execute the model |
Running within the observer object is our model. The key object in our model is the model space object. The Model Space is a rectangular grid depicting the agents environment onto which other model objects are mapped. Its attributes and algorithms are described in table 2. Individual bands are placed into cells in the model space as they move about the landscape. Other objects, such as Landmarks, and Food Cells are overlaid on the Model Space and displayed on the common interface provided by the observer object. The dimensions of the grid are set by a pair of parameters. For most trials, a 128 by 128 model space has been used. Practical considerations of the data analysis software preclude large dimensions at this time.
The band model object attributes contain statistics that describe overall model behavior such as the number of bands that are dead, the life span of a band, the number of elapsed days in the model among others. In addition there are attributes that point to a lists of the current bands, the individual agents that comprise them, the current landmarks, and resource cells respectively. These constitute the basic model objects. In subsequent sections we will discuss the attributes and algorithms associated with each. There are also pointers to files that will be used to retrieve model data and archive results. Finally, the model parameter pointer references the list of model parameters that can be set upon model initialization and govern the interaction of the model objects.
The algorithms for the model space object are in charge of getting the
model parameters, initializing the model according to those parameters,
updating the model statistics after each model event, and logging diagnostic
information about model performance that can be useful in debugging the
model.
| Object attributes | |
| Attribute | Description and usage |
| Day Number | Counter of the current day in the model. |
| Number of Dead Bands | Current count of the number of dead bands |
| Number of bands that have died. | Count of the total number of bands that have died since the beginning of the model. |
| Sum of band age at death | Sum of the age of all dead bands at the time of their death. Used to calculate average mortality. |
| Average age of band at death | Average age of bands that have died or are still living. |
| List Food Spaces | Pointers to the Food Space Objects |
| List of Landmarks | Pointer to the list of landmarks. |
| File object pointer | Pointer to the file control object |
| Maximum distance | The calculate diagonal distance across the landscape |
| Model parameters | Shared elements that can be set at the start of the simulation run to control the operation of the model. |
| Model Parameters | |
| Parameter Name | Parameter Description |
| BandSize | maximum size of each band (number of members) |
| BandSplit | size at which band can split |
| BandStart | size of each band at the beginning of the run (number of members) |
| BaseMDReq | base minimum daily food requirement for an adult |
| BounceMode | Behavior mode when a band reaches
the edge of the space or collides with another band
0 – reflex bounce 1 – vote on a new direction |
| CAAcceptanceInterval | Cultural Algorithm Acceptance Interval (days) this is the interval at which the CA component accesses the data in the model space |
| CAInfluenceInterval | Cultural Algorithm Influence Interval (days) this is the interval at which the CA component provides feedback to the model space |
| CAMode | Selects the CA algorithm to be used, |
| caption | Trial Caption |
| consumeMode | mode of consumption during foraging |
| daysAhead | Number of days of consumption that an individual can stockpile to recover from shortfalls or to get ahead |
| daysToDie | number of days without MDR before a guy dies |
| decayDays | number of days for a dead band to decay and disappear from the display until this interval expires, the square occupied by the band is blocked to other bands |
| diagBand | A band number to trigger diagnostic outputs that are limited to a selected band |
| diagnosticDest | destination for diagnostic outputs
1 = > console
|
| diagnosticInterval | diagnostic interval in days, interval at which diagnostic outputs will be written |
| diagnosticMask | diagnostic mask, a bitmap selecting various classes of diagnostic outputs |
| flipMode | select a yes no parameter to be flipped for each trial |
| foodDistFactor | First computational factor for food distribution. Used differently by each mode. Not always used. |
| foodDistFactor2 | Second computational factor for food distribution. Used differently by each mode. Not always used. |
| foodDistMode | food distribution function |
| foodDistRange | food distribution range in squares
usage varies by algorithm currently used only for mode 6, patchwork around Lankmarks to control the size of the patches |
| foodMaxValue | The maximum quantity of food that can exist in a single cell |
| forageMax | number of squares to forage in Mode 1 |
| forageMode | forage mode
0=en mass while traveling 1=individual after traveling (unimplemented) |
| lmDistMode | landmark distribution mode |
| lmPerMemory | controls how many landmarks are attached to a memory when it is formed |
| logDataInterval | interval to write to data log (days) |
| memDepth | memory depth in days, number of days after a memory is formed before it is forgotten |
| memMode | Memory formation mode |
| numBands | number of bands to generate |
| numLandmarks | number of landmarks to generate |
| quitAfter | Terminate the mode after this many steps. Results in program failure. Superseded by batch mode operation. |
| randomDays | number of days of random movement before using memory (during this interval, bands do not starve) |
| regenRate | rate of food regeneration per day (<= 1.0) |
| reincarnateDays | number of days before a dead band is reincarnated |
| reproduceDays | Number of days where the band is fully fed before it can add a member. |
| searchMode | search mode |
| seedProb | probability of food in a cell
(random distribution) also controls the minumum amount of food
not currently used in other modes |
| starveMode | Mode for determining starvation |
| stepsPerDay | maximum number of steps to move in one day |
| stopEvery | interval (days) at which the model will pause |
| trialName | file name prefix for the trial
(yyyymmdd_hhmmss)
this is not specified externally, but is generated and exported at run time |
| visibility | default landmark visibility in squares, for how many squares is a landmark visible |
| vision | default vision in squares, how many squares can a Guy see a landmark |
| worldXSize | X dimension of the model space |
| worldYSize | Y dimension of the model space |
| ZoomFactor | swarm zoom factor, 0 = automatic
1- |
| Object algorithms | |
| Attribute | Description and usage |
| Get methods | Obtain model parameters and control variables |
| Set methods | Set model parameters and control variables |
| Diagnostic methods | Log diagnostic information about model execution |
| Tracking methods | Maintain global information on model execution, such as number of living bands, etc. |
Now each of the model objects that interact within the grid world will be described. The basic objects are: the food space cells, the landmarks, and the bands. The bands are composed of individual member agents and each member agent has a list of memories. We will now describe each of these objects in turn starting with the top level model objects.
The Food Space is a rectangular grid that overlays the Model
Space. Each cell in the food space contains a quantity of food that can
be consumed. Two supplemental food spaces are defined to support variation
in the food supply. The first of these contains the original values calculated
when the Food Space was populated. This is used to control the re-growth
of food after it has been consumed. The second is used to support seasonal
variation of the food supply.
| Object attributes | |
| Attribute | Description and usage |
| Current food values | Array containing the amount of food available in each cell of the landscape. |
| Maximum food values | Array containing the permitted maximum amount of food for each cell of the landscape. |
| Object algorithms | |
| Algorithm | Description and usage |
| Seed food space | A group of methods that seed the food space according to the selected distribution function |
| Regenerate | Grow more food to make up for the amount of food consumed. Executed daily. |
| Vary food | Change the available food according to a seasonal cycle. |
| Get methods | Obtain model parameters and control variables |
| Set methods | Set model parameters and control variables |
| Diagnostic methods | Log diagnostic information about model execution |
Just as the food cells are overlaid onto the model grid, so are the landmarks. Landmarks are randomly distributed throughout the landscape. They are commonly observed landscape features that can be used as reference points in the decision making of the bands. While landmarks can be randomly placed within the landscape, certain landmarks were placed in certain grid positions to ensure that the entire region was potentially exploited by the bands. For example, a Landmark is placed in each corner square of the landscape. This choice was based on early observation that bands could not navigate into the corners of the space unless their was a Landmark towards which they could move.
Landmarks are used to support memory formation and band navigation. Each memory references one or more landmarks that are visible from the location where the memory was formed. All navigational choices made by individuals are made on the basis of moving towards or away from a landmark.
Each landmark is an object whose state is described in terms of its
position on the grid, the maximum distance from which it can be viewed,
along with a list of memory scores that have been produced by individuals
within view of the landmark. The basic algorithms for landmarks are their
distribution (randomization), and the collection of statistics about their
use in decision making. Currently landmarks are viewed as staic objects
so degradation or improvement in their visualization appears over time.
| Object attributes | |
| Attribute | Description and usage |
| Position | X and Y coordinates of the landmark |
| Visibility | Distance at which the landmark is visible |
| Landmark scores | Information about the quality of memories associated with the landmark. |
| Object algorithms | |
| Attribute | Description and usage |
| Distribute landmarks | Distribute the landmarks more or less randomly on the space. |
| Landmark statistics | A series of methods that maintain current and prior history on landmark performance in memory searches. |
While the positions of both food cell and landmarks do not change during the course of the simulation, the bands are able to move about in search of food. Bands are groups of individual hunter-gatherer agents. The members of a band move and forage together within a cell. At the beginning of a simulation run, bands are placed at random on the landscape. Since the carrying capacity of the environment can be estimated, the number of bands used will influence the selective pressure on the decision making process here. In all of the runs described here, more individuals are initially present than can be supported by the environment. This was done in order to assess therobustness of the vector voting model under duress.
Each band starts with a specified number of members. This number can be reduced by the death of members or increased by the addition of new members. Both the addition and deletion of members results from the foraging activity. If the group fails to meet the MDR for some of its members over a period of time, deaths can result. If all members of a band die, the band is removed from the model. New members can be added to a band whenever all members of the band have received their minimum daily requirement for a specified number of days. Only one member is added, and the interval starts over. When the band size reaches a maximum, fission can take place where the new band is placed in the location of a deceased band.
Since band decision making is at the heart of the model, the band object
is the most complex model object here. Table 5 gives
its attributes and its algorithms. A number of band attributes relate to
its current status in terms of creation, number of members and a pointer
to a list of it members, current direction of movement, and number of members
fed among others. Random days is an attribute that determines how many
days the group will move at random before decision making via vector voting
begins. The random movement simulates the discovery of the new territory
by the band and allows them to record memories about their experience which
serve as the fuel for the decision making process. Random days is an attribute
that determines how many days they forage randomly until decision making
begins. For the completely random model, the number of days is equal to
that of the simulation length. The band algorithms include methods for
initializing a new band, starting a day, finishing a day, updating its
members daily information among others.
| Band object attributes | |
| Attribute | Description and usage |
| Size | The maximum permitted size of the band. |
| Member list | Points to the guys in the band |
| Random days | The number of days of random motion to be performed before using the search algorithm. Zero for all recent trials. |
| Total Daily Requirement | The total amount of food required by the band on a single day |
| Band dead | An indicator that the band has died |
| Band decayed | An indicator that the band has been dead long enough to be removed from the display and also long enough to be reincarnated. |
| Day created | The model day on which the band was create or reincarnated |
| Direction | The current direction of movement for the band |
| Days fed | The number of days during which the all members of the band have received their MDR. |
| Have eaten | Indicator of whether the members of the band received the MDR today |
| Number dead | The number of members in the band who are currently not alive. |
| Number in and | The number of members in the band who are currently alive |
| Consumption order controls | Controls the order in which members are fed. |
| Contact information | Counters of the number of times the band collided with or was next to another band |
| Day band died | The day on which the band died. Used to control reincarnation of bands. |
| Range date | Deflections in the X and Y axis during a measurement period. |
| Band object algorithms | |
| Algorithm | Description and usage |
| Get methods | Obtain model parameters and control variables |
| Set methods | Set model parameters and control variables |
| Diagnostic methods | Log diagnostic information about model execution |
| Maintain count of alive and dead | Methods to maintain the current living population of the band |
| Select direction | Method to obtain and tally votes from the band members |
| Step | Method to perform one step’s processing for the band, including movement and consumption |
| Start day | Method to control beginning of day processing, including selection of direction |
| End day | Method to control end of day processing, including memory formation by band members |
| Reincarnate | Reincarnate a band that has previously died. |
| Forage | Consume food at the end of a day’s movement (unimplemented future function.) |
| Maintain movement and contact statistics | Group of methods to maintain statistics on range of movement and contact with other bands. |
| Reproduce | Method to add a member to a band during good times. |
Agents are individual members of a band. They are the second most complex
model objects. Each member object forms memories based on how much
food it receives on a given day. A number of variables describe the state
of an agent including their age and gender, the MDR for their category,
where they are located, the landmarks that are visible from their current
location, the amount of food they have gotten today, the memories that
they have of their experiences, and how they have voted in terms of the
bands decision making. The algorithms for an individual agent include making
memories, consuming food, starting the day, ending the day, their vote
in the foraging decision, and other algorithms to compute agent statistics.
The description of the agent object attributes and algorithms are given
in table 6 below.
| Object attributes | |
| Attribute | Description and usage |
| Adult | Flag indicating whether the member is and adult of a child |
| Gender | Flag indicating whether the member is male of female |
| MDR | Minimum Daily Requirement of food |
| Memory list | List of memories |
| Vision | Number of square in the landscape that the individual can see a landmark. Not used in any current models. |
| Food consumed today | Amount of food consumed today |
| Days without food | Number of days during which the member has not received the MDR |
| Dead | Indicates whether the individual is dead |
| Food deficit | Cumulative shortfall of consumption against MDR |
| Number of Memories | Current number of memory entries for this individual. Used to gather model statistics |
| Last vote | Holds the last direction the member voted for. Use to calculate dissatisfaction. |
| Total dissatisfaction | Cumulative total of dissatisfaction. Used to determine consumption order. |
| Object algorithms | |
| Attribute | Description and usage |
| Get methods | Obtain model parameters and control variables |
| Set methods | Set model parameters and control variables |
| Diagnostic methods | Log diagnostic information about model execution |
| Vote for a direction | Decide which way the member wants to travel |
| Make a memory | Create a memory based on current location and today’s consumption experience. |
| Start of day | Perform start of day processing, including clearing of consumption counters |
| End of day | Perform end of day processing, including calculation of satisfaction |
| Consume food | Consume food up to the MDR |
| Consume more food | Consume food beyond the MDR if it is available, up to the permitted multiplier |
| Forage | Look for food at the end of a day’s movement (unimplemented future function) |
| Food needed | Calculate the current need for food. Used to control consumption order |
| Check whether fed | Compare the amount consumed with the MDR |
| Reproduce | Change status from dead to living, resetting all controls |
Just as band objects are contained in the model grid, and agent objects
make up the bands, each agent has a list of memories that guides
their decision making. At the end of each day's movement, every member
forms a memory. The content of this memory is a score that indicates how
well the individual was fed on that day along with the landmarks associated
with the memory by the individual (good), the x and y location in which
the memory was formed, and the list of landmarks associated with the memory
by the individual. The basic algorithms for this object are the addition
and deletion of memories. This constitutes the emulative learning component
of the model.The description of the memory object attributes and algorithms
are given in table 7.
| Object attributes | |
| Attribute | Description and usage |
| Get methods | Obtain model parameters and control variables |
| Set methods | Set model parameters and control variables |
| Diagnostic methods | Log diagnostic information about model execution |
| Active indicator | Indicates whether the memory is active or expired |
| Directions | Direction of movement into and out of the square where the memory was formed (unimplemented future function) |
| Good | Score reflecting the food consumption associated
with the memory
–5 – obtained no food +5 – obtained as much extra food as was allowed. |
| Landmark list | List of landmarks associated with the memory. Used to select memories for navigation. |
| Position | X and Y position at which the memory is formed. This is maintained but is not used when interpreting a memory. |
| Object algorithms | |
| Attribute | Description and usage |
| Get methods | Obtain model parameters and control variables |
| Set methods | Set model parameters and control variables |
| Diagnostic methods | Log diagnostic information about model execution |
| Reincarnate | Clear memories as part of the band reincarnation process |
| Add a landmark | Associate a landmark with a memory |
This concludes the basic description of the objects used to support the Band simulation model in the swarm environment. In the following section we use the simulation model to ask various questions about the capabilities of the vector voting model when used in conjunction with emulative learning.
In general, a set of 10 trials has been used for each of the two experiments.
For each trial, a pair of simulations were run. The same random number
seed was used for each of the trial pair. For example, for the first set
of experiments the trial pair will be a vector voting model and a random
walk model. The results of each series are averaged to produce a result
set for analysis. The food and landmark distributions are held constant
for a group of trials so that scoring of landmarks and interpretation of
patterns of movement can be compared.
Figure 2. An example of the patchwork distribution
used in the runs.
| Parameter Name | Parameter Description | Parameter Value 1 | Parameter Value Description 1 | Parameter Value 2 | Parameter Value Description 2 | Mismatch |
| bandSize | maximum size of each band (number of members) | 6 | 6 | |||
| bandSplit | size at which band can split | 0 | 0 | |||
| bandStart | size of each band at the beginning of the run (number of members) | 3 | 3 | |||
| baseMDReq | base minimum daily food requirement for an adult | 1500 | 1500 | |||
| beliefOption | Belief Space Option - unimplemented | 0 | 0 | |||
| bounceMode | Behavior mode when a band reaches the edge of the space or collides with another band | 1 | make new decision on bounce | 1 | make new decision on bounce | |
| CAAcceptanceInterval | Cultural Algorithm Acceptance Interval (days) this is the interval at which the CA component accesses the data in the model space | 10 | 10 | |||
| CAInfluenceInterval | Cultural Algorithm Influence Interval (days) this is the interval at which the CA component provides feedback to the model space | 100 | 100 | |||
| CAMode | Selects the CA algorithm to be used, | 1 | basic landmark history | 1 | basic landmark history | |
| caption | Trial Caption | Memory Based Search | Random Search | YES | ||
| consumeMode | mode of consumption during foraging | 0 | fixed order | 0 | fixed order | |
| daysAhead | Number of days of consumption that an individual can stockpile to recover from shortfalls or to get ahead | 2 | 2 | |||
| daysPerYear | Number of days per year for seasonal variation | 0 | 0 | |||
| daysToDie | number of days without MDR before a guy dies | 7 | 7 | |||
| decayDays | number of days for a dead band to decay and disappear from the display until this interval expires, the square occupied by the band is blocked to other bands | 7 | 7 | |||
| diagBand | A band number to trigger diagnostic outputs that are limited to a selected band | 0 | 0 | |||
| diagLM | Diagnostic Landmark Number | 0 | 0 | |||
| diagnosticDest | destination for diagnostic
outputs
1 = > console 2 => log, 3 => both |
0 | 0 | |||
| diagnosticInterval | diagnostic interval in days, interval at which diagnostic outputs will be written | 10 | 10 | |||
| diagnosticMask | diagnostic mask, a bitmap selecting various classes of diagnostic outputs | 0 | 0 | |||
| flipMode | select a yes no parameter to be flipped for each trial | 0 | No Parameter Flipping | 0 | No Parameter Flipping | |
| foodDistFactor | First computational factor for food distribution. Used differently by each mode. Not always used. | 0.5 | 0.5 | |||
| foodDistFactor2 | Second computational factor for food distribution. Used differently by each mode. Not always used. | 0.5 | 0.5 | |||
| foodDistMode | food distribution function | 6 | patchwork around landmarks | 6 | patchwork around landmarks | |
| foodDistRange | food distribution
range in squares
usage varies by algorithm currently used only for mode 6, patchwork around Lankmarks to control the size of the patches |
12 | 12 | |||
| foodMaxValue | The maximum quantity of food that can exist in a single cell | 16384 | 16384 | |||
| foodVarFactor1 | Food variation factor 1 | 0 | 0 | |||
| foodVarFactor2 | Food variation factor 2 | 0 | 0 | |||
| foodVarMode | Vood Variation Mode | 0 | 0 | |||
| forageMax | number of squares to forage in Mode 1 | 0 | 0 | |||
| forageMode | forage mode
0=en mass while traveling 1=individual after traveling (unimplemented) |
0 | 0 | |||
| goodMode | Mode for calculating good scores | 0 | 0 | |||
| lmDistMode | landmark distribution mode | 0 | random (seeded corners) | 0 | random (seeded corners) | |
| lmPerMemory | controls how many landmarks are attached to a memory when it is formed | 2 | 2 | |||
| logDataInterval | interval to write to data log (days) | 0 | 0 | |||
| memDepth | memory depth in days, number of days after a memory is formed before it is forgotten | 64 | 64 | |||
| memMode | Memory formation mode | 0 | use n closest landmarks in any direction | 0 | use n closest landmarks in any direction | |
| numBands | number of bands to generate | 128 | 128 | |||
| numLandmarks | number of landmarks to generate | 128 | 128 | |||
| quitAfter | Terminate the mode after this many steps. Results in program failure. Superseded by batch mode operation. | 0 | 0 | |||
| randomDays | number of days of random movement before using memory (during this interval, bands do not starve) | 0 | 0 | |||
| regenRate | rate of food regeneration per day (<= 1.0) | 0.05 | 0.05 | |||
| reincarnateDays | number of days before a dead band is reincarnated | 9999 | 9999 | |||
| reproduceDays | Number of days where the band is fully fed before it can add a member. | 10 | 10 | |||
| searchMode | search mode | 1 | memory based vector voting | 0 | random | YES |
| seedProb | probability of food
in a cell (random distribution) also controls the minumum amount of food
not currently used in other modes |
1 | 1 | |||
| starveMode | Mode for determining starvation | 1 | deficit > MDR * days to die | 1 | deficit > MDR * days to die | |
| stepsPerDay | maximum number of steps to move in one day | 4 | 4 | |||
| stopEvery | interval (days) at which the model will pause | 100 | 100 | |||
| trialName | file name prefix for
the trial (yyyymmdd_hhmmss)
this is not specified externally, but is generated and exported at run time |
20010213_201544 | 20010213_200222 | YES | ||
| visibility | default landmark visibility in squares, for how many squares is a landmark visible | 32 | 32 | |||
| vision | default vision in squares, how many squares can a Guy see a landmark | 32 | 32 | |||
| voteMode | Voting mode (unimplemented) | 0 | 0 | |||
| worldXSize | X dimension of the model space | 128 | 128 | |||
| worldYSize | Y dimension of the model space | 128 | 128 | |||
| zoomFactor | swarm zoom factor, 0 = automatic | 0 | 0 |
As we might expect, a memory directed search performs significantly better than random movement in almost all food landscapes. The one exception is that if the food distribution is completely randomized, there is no advantage to the memory directed search. However, in all of the examples given here, the global distribution of resources is random, but the local distribution of resources is patterned. The question is whether the vector voting model can outperform the random walk model even when there is just local patterning. If it can, then it should do even better when region-level patterns are present. The following diagrams compare metrics averaged over the 10 trials between the random walk (random search) and vector voting search (memory based search) models for the locally patterned patchwork examples.
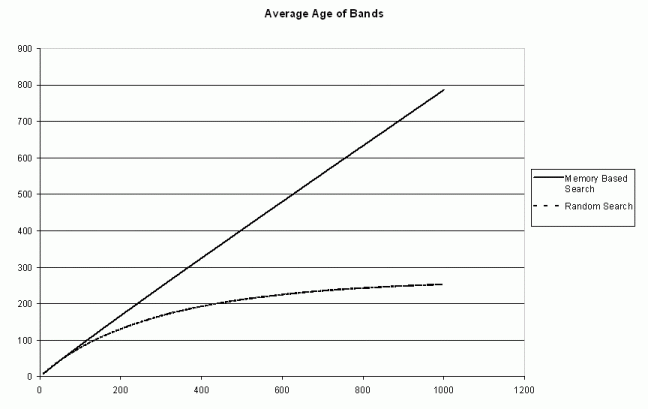
Figure 3. The average age of model bands
over a 1200 day simulation for the vector voting (memory based) and random
walk (random search) models.
Figure 3 shows the average survival age of bands during the execution of the model. This calculation is an average of the age of bands at the time they died as well as the age of each surviving band. The curve for the random model flattens out over time indicating that the age of current bands is contributing less and less to the sum. In other words, the number of surviving band is approaching 0. On the other hand, the age of the surviving bands for the vector voting model is producing a relatively constant increment to the sum over the 1000 model days. That is, a consistent percentage of bands are surviving year after year.
Figure 4 shows the number of individuals getting fed over all bands for each year. The carrying capacity for the environment is approximately 300 individuals. Our initial population was 384, slightly over the maximum amount that we estimated could be supported by the environment on a continuous basis. So, it provides some initial selective pressure on the bands. Initially, the foraging is random in order to gather information for use in decision making. Since all of the food cells are at the maximum at onset the groups are able to increase the number of individuals getting their maximum daily requirements. However, once foraging has started to deplete the resources, the number of individuals getting fed tends to converge to around 200 for the vector voting model, about 100 less than the total carrying capacity. By the addition of more landmarks and the proper selection of the sharing algorithm, the system can plateau at even higher levels, approaching 300 as the maximum plateau. The number of indiivudals fed by the random walk model continues to decrease approaches 0 as an equilibrium point. Although it is clear that the environment can support more than that, the system has not been able to acquire sufficient information to exploit those patterns.
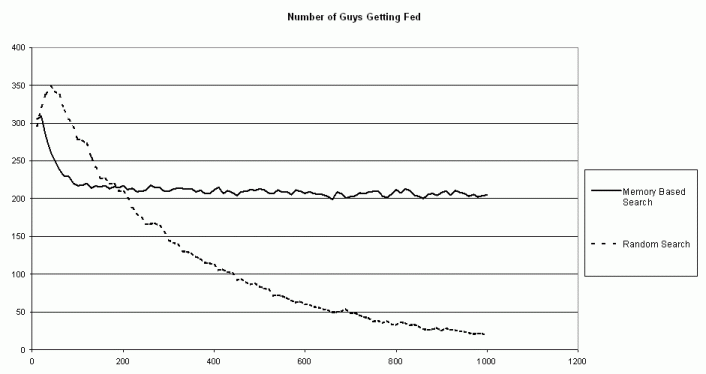
Figure 4. Average number of band members
getting fed in the region over 10 runs each for the vector voting and random
walk models.
Figure 5 shows the number of band members that were alive on each day of the model execution. Notice that in both cases the numbers of individuals alive exceeds the number of individuals getting fed. For the vector voting model, this number tends to plateau out around 260 here, about 40 less than the carrying capacity. The key is that in any one point in time not all individuals are getting fed, but enough get fed frequently enough in order to allow the overall population to plateau at a higher level than that for those getting fed. The random model again approaches an equilibrium of 0 as the difference between the number of those getting fed and those alive becomes 0 as does the population.
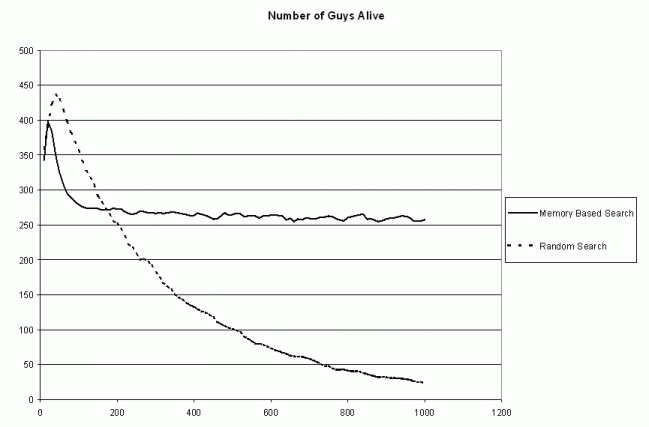
Figure 5. The average number of individuals
alive for each model year in the vector voting (memory based) and random
walk ( search) models for 1200 days.
The results above demonstrate the effectiveness of the memory based search algorithm in finding food in a harsh but consistent environment. The vector voting model is able to exploit sufficient local patterning of resources in order to produce a suggested equilibrium population of around 260, just under carrying capacity. All of the bands without any memory based decision making died out even though the environment was able to support a proportion of them.
Mode 0 - Band members are fed in a fixed order on each turn.All simulations were run using a memory based search with a patchwork food distribution.Mode 1 - Band members receive equal shares of the food on each turn.
Mode 2 - The band members with the largest food deficit are fed first on each turn.
Mode 3 - The band members who wanted to travel in the chosen direction are fed first on each turn.
Mode 4 - The band members are fed in a fixed order, starting with a different member in rotation on each turn.
Figure 6 Shows the rate of survival for each of the five distribution modes. The vertical axis is the number of surviving band members and the horizontal axis is the day number.
One of the key things to note is that the performance of the vector voting model is markedly affected by how the resources are shared among the individuals in a band. This is due to the fact that there is no sharing of information among band members concerning the memories that brought about the decision of each. Thus, if individuals who are making bad choices are rewarded as much as those who are making good ones, it is likely that a member making a good choice will die and their memories will be lost to the group forever. Thus, both the round robin and equal sharing paradigms cause the number of individuals to be supported by vector voting models to converge to 0. This is equivalent to the random walk model. This is because the loss of key individuals is causing the decision making to behave in a random manner.
On the other hand, by rewarding the individuals who contributed to the winning decision we are rewarding the providers of key information and working to preserve the groups information that is stored at the individual level. Thus, satisfied first performs the best of the five, producing overall population levels approximately equal to the carrying capacity of the environment. In this case, vector voting exploits the local patterning of resources and satisfied first supports the retention of this information at the local level. "Survival of the fittest" in the case where there is no shared information between individuals means "survival of the group".
Fixed or rank order access to resources performs slightly less than the satisfied first paradigm, but not much less. It is also easier to enforce since one doesn't have to poll the members and decide who did what, where and when. Thus, fixed rank is a good fit with the vector voting model since it produces performance comparable to the satisfied first approach without the social overhead.
The neediest first paradigm is midway between the two groups. Once the population size is significantly below carrying capacity, the vector voting model allows sufficient exploitation of the environment to allow most individuals to be fed. Thus, the randomness that is introduced into the decision-making process is balanced out by the individuals that are helped through the process. Notice that if the group is allowed to share their detailed memories via language, the relative performance of this more altruistic strategy will improve.
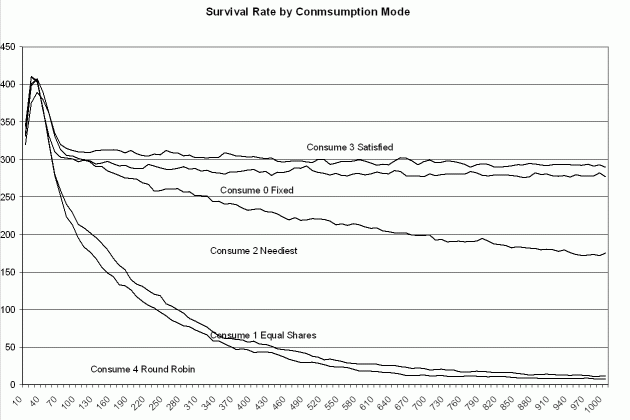
Figure 6. The average number of individuals
in the population over 10 runs for each of the 5 food distribution modes.
The vector voting model, while exploiting local patterns effectively, is very sensitive to the resource distribution system used. This is because individual knowledge is not shared. This means that if resources produced by the vector voting approach are shared without any consideration of the individuals who made the decisions in the first place, the individuals and their attendant information can be lost introducing randomness into the process and ultimately generating performance that can be the same as a random walk. Thus survival of the fittest is synonymous with survival of the group when information is not sharable.
Also, there are two resource sharing strategies, satisfied first and rank order, that tend to produce the results that are closest to the carrying capacity. While the satisfied first approach is the most precise way to reward the individual responsible for a groups success, and in turn preserving the information that they used, it requires a certain amount of overhead to manage and enforce. A fixed or rank ordering of access to resources produces results that are slightly, but not much lower, and with less overhead in terms of how to determine allocation.
The next step in our project is to implement the Cultural Algorithm paradigm which allows the individuals to pool their memories. Theoretically, this sharing of information will allow the group to make regional decisions about certain predicates more reliably than in the vector voting model. In particular, the pooling of information via a belief space will allow the group to decide on predicates that are not tied to particular locations , e.g. norms of behavior, within the environment. These are called position invariant predicates. Being able to do this makes imitative learning , a form of learning largely unique to the human species, possible [5]. Both activities are influenced by the structure of the language used to perform the pooling and within which the learned information can be articulated. This will be the subject of a subsequent paper.
Also, it will be of interest to see how the introduction of shared information impacts the relative utility of the resource distribution modes. That is, will equal access to knowledge within the group imply that equal access to resources will provide better support for group decision making than it currently does in a vector voting environment.
[2] Tomasello, M., (1999) The Human Adaptation for Culture, Annual Review of Anthropology, Vol. 28:509-529.
[3] Kummer, Hans, Primate Socieities, New York, Aldine Press, 1968.
[4] Reynolds, R. G., and Zeigler, B. P. (1979) A Formal Model for the Operation of Consensus-Based Hunting-Gathering Bands, in C. Rebfrew, K. Cooke (eds) Transformations: Mathematical Approaches to Culture Change, New York, Academic Press, pp:405-418
[5] Pedone, R., and Conte, R. (2000)The Simmel Effect:
Imitation and Avoidance in Social Hierarchies, paper to be presented at
Workshop on Cultural Transmission, Sienna, Italy.