Baldassarre,
G. (2001). Cultural evolution of 'guiding criteria' and behaviour in a
population of neural-network agents.
Journal of Memetics - Evolutionary Models of Information Transmission, 4.
http://cfpm.org/jom-emit/2001/vol4/baldassarre_g.html
Baldassarre,
G. (2001). Cultural evolution of 'guiding criteria' and behaviour in a
population of neural-network agents.
An important form of cultural evolution involves individual learning of behaviour by the members of a population of agents and cultural transmission of learned behaviour to the following generations. The selection of behaviours generated in the process of individual learning requires some "guiding criteria". As with behaviour, guiding criteria can be innate or originate from individual or social learning. Guiding criteria play a fundamental role in cultural evolution because they strongly contribute to determine the behaviours that will enter the pool of cultural traits of the population. This work presents a computational model that investigates the nature and function of some forms of "guiding criteria" in the cultural evolution of a population of agents that learn and adapt to the environment using neural networks. The model focuses on the interplay of individual learning and cultural transmission of behaviour and those forms of guiding criteria. The model contributes to clarify the nature and role in culture evolution of the guiding criteria studied. Also, within the assumptions of the model, it shows that the cultural transmission of behaviour is more effective than the transmission of the guiding criteria.Keywords: Multi-agent simulation, neural networks, cultural evolution, cultural transmission, reinforcement learning, imitation, behaviour, guiding criteria, values, evaluations.
Boyd and Richerson (1985, page 132 and 136) underline the importance of "guiding criteria" in the process of individual learning and cultural evolution. They argue that guiding criteria are things like the "sense of pleasure and pain that allows individuals to select among variants", where these (behavioural) variants are generated in the process of individual learning or observed in other individuals. Guiding criteria play a central role in cultural evolution because by determining which behaviours are kept and which are discarded during individual learning, they strongly affect the cultural traits that enter the population's pool of traits through guided variation (this is the focus of this work). The same guiding criteria are also used for the selection of cultural traits in other forms of cultural evolution, such as direct bias (this is not investigated here).
Despite the importance of guiding criteria, Boyd and Richerson do not give a precise description of their nature and origin. They only say that they "could be inherited genetically or culturally or learned individually". Guiding criteria, as their name hints, are a complex compound concept that will require much investigation to be fully understood. The goal of this paper is (a) to contribute to this investigation by presenting a computational model that, by drawing from the biological models of animal learning, defines the nature of some guiding criteria and (b) to study the role of such guiding criteria in the cultural evolution of behaviour.
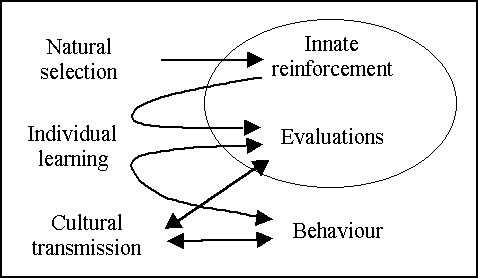
The processes studied in this work are summarised in figure 1. The model used in this investigation mimics a population of artificial agents that adapt to the environment by learning to search for "good" food and to avoid "bad" food. This process of learning is based on an innate capacity to judge the food as good or bad tasting. The capacity to search and avoid food can also be acquired by imitating other agents. Two kinds of guiding criteria are studied in the model. The first is "reinforcement", widely studied in animal learning literature (Lieberman, 1993, for a review). Reinforcement roughly corresponds to an internal neural activation of the agent's brain associated with pleasure or pain. The neural mechanisms underlying this activation are mainly innate (Rolls, 1999). The second kind of guiding criteria are "evaluations" of the perceived state of the world. An evaluation is an internal neural activation of the agent's brain that quantifies the potential of that state to deliver reward in the future. As with the searching and avoiding behaviour, the capacity to express correct evaluations can be learned individually or socially from other agents. As we shall see, the capacities to perform correct evaluations and to exhibit adaptive behaviour are closely related. The study focuses on the effects that the cultural transmission of evaluations and behaviour produces on the level of adaptation of the whole population.
Section two describes the computational models used in the simulations and in particular the neural network controlling the agents and the algorithms mimicking individual learning, imitation, and the transmission of evaluations. Section three presents the results of the simulations and their possible interpretation. Section four describes some related work and, finally, section five draws the conclusions.
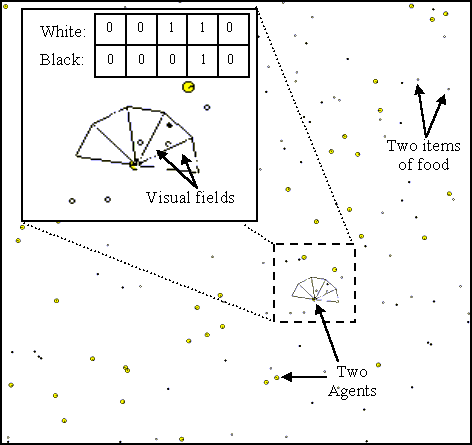
Figure 2: The environment (1x1) with the agents and food items
(radius 0.005 and 0.0025 respectively). The "zoom window" shows the 5 visual
fields of the 5 white and black pairs of sensors of one agent, and their
activation.
In the simulations, succeeding generations of agents (overlapping in time) live in the environment. Each agent is capable of learning to search for good food and to avoid bad food during its life (individual learning). Also it is capable of learning this capacity from its (only) parent (cultural transmission).
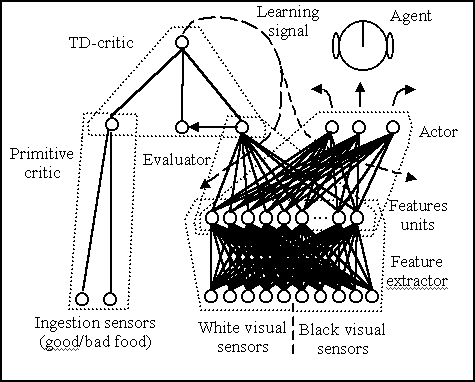
Figure 3: The neural architecture controlling an agent. The
circles and arcs represent neurons and connections. The dotted arrows represent
the learning signal that allows updating the weights of the evaluator and
the actor.
The primitive critic incorporates the guiding criterion of reinforcement considered previously. This guiding criterion is innate. The primitive critic is made up of a simple neural network with two input units (one for the good-tasting food, g, and one for the bad-tasting food, b) and one output unit, r. The input units assume the value of 1 when an item of the corresponding (good or bad) food is ingested and a value of 0 otherwise. The two (innate) connection weights wg and wb are set to the value +1 and -1 respectively, so that a reward or punishment ("pleasure" or "pain") is signalled by the linear output unit when an item of good or bad food is ingested. The activation of the output unit is computed as follows:
(1) r = wg g + wb b
The feature extractor takes the 10 signals from the visual sensors as input and implements a "Kanerva re-coding" of them (Sutton and Barto, 1998). The (innate) weights of the feature extractor are randomly drawn from the set {0, 1}. Each of the feature units (150 in the simulation) activates with 1 if the Hamming distance (standardised to 1 by dividing it by the number of feature units. The Hamming distance between two binary arrays is the number of elements with same position but different values) between the input pattern and the "prototype" encoded by its weights is less than a certain threshold (0.4 in the simulations). If the Hamming distance is greater then the threshold then the feature unit activates with 0. The main function of the feature extractor is to map the input space into a space with a higher dimensionality so to avoid eventual problems of non-linear separability and to attenuate interference problems during learning (Sutton and Barto, 1998).
The actor that is equivalent to the agent's action-selection policy (behaviour), is a two-layer feed-forward neural network that takes the activation of the feature units as input and has three sigmoidal output units that locally encode the three actions. To select one action, the activation pk (interpretable as "action merit") of the three output units is used in a stochastic winner-take-all competition. The probability P[.] that a given action ag among the ak actions becomes the winning action aw is given by:
(2) P[ag = aw] = pg
/ 
kpk
The evaluator incorporates the second kind of guiding criteria considered
in this work, the "evaluations". An evaluation is a measure of the potential
of a state of the world to deliver future reward or punishment. The evaluator
is a two-layer feed-forward neural network that gets the activation of
the feature units as input. With its linear output unit it learns to express
the estimation V'
[st]
of the evaluation V[st]
of the current state st. V[st]
is defined as the expected discounted sum of all future reinforcements
r, given the current action-selection policy 
expressed by the actor:
(3) V[st]
= E[
0rt+1
+1rt+2
+2rt+3
+ ...]
where 
(0, 1) is the discount factor, set to 0.95 in the simulations, and E[.]
is the mean operator.
The TD-critic is an implementation in neural terms (weights to be considered as innate) of the computation of the Temporal-Difference error e defined as (Sutton and Barto, 1998):
(4) et = (rt+1
+ V'[st+1])
- V'[st]
The evaluator is trained with a Widrow-Hoff algorithm (Widrow
and Hoff, 1960) that uses as error the error signal coming from the
TD-critic. The weights wi are updated so that the estimation V'[st]
expressed at time t by the evaluator, tends to be closer to the target
value (rt+1+ V'[st+1]).
This target is a more precise evaluation of st because it is expressed
at time t+1 on the basis of the observed rt+1
and the new estimation V'[st+1].
The formula of the updating rule is:
(5) 
wi
= 
etyi
where is
a learning rate (set to 0.01 in the simulation) and yi
is the activation of the feature unit i. This algorithm implements
the individual learning of the evaluations. The idea behind this algorithm
can be explained by assuming that the action-selection policy expressed
by the actor is fixed. At the beginning of the simulation the weights of
the evaluator are set randomly so it will associate evaluations close to
0 to each perceived state of the world (in fact its transfer function is
linear). The first time that the agent bumps into a good (or bad) item
of food, it perceives a reward of +1 (or -1), so the TD-critic expresses
an error of about +1 (or -1). Given this error, the evaluator learns to
associate a higher (or lower) evaluation to the state of the world that
preceded the one where the food was ingested. The next time that this state
is perceived, it will cause the state preceding it to be evaluated with
a higher (or lower) evaluation. This process will continue in a backward
fashion so that the agent will finally assign positive (or negative) decreasing
(because of the discount factor) evaluations to the sequence of states
preceding the ingestion of good (or bad) food.
The actor is also trained according to the error signal coming from
the TD-critic, so that the action-selection policy is improved with experience.
At the beginning of the simulation the actors' weights are set randomly,
so the output units have an activation close to 0.5 for each input pattern
(because its transfer function is sigmoid), and the probability of selecting
each of the three actions is close to 0.33. This induces the actor to explore
the environment randomly. Given that the evaluator (once it has been trained)
expresses an evaluation V'[st]
of st according to the average effect of the actions
that the actor selects in association with st, an error et
> 0 means that the selected action aw has led to a new state of the world
st+1
(evaluated rt+1 + V'[st+1])
that is better than the one previously experienced after st. In this case
the probability of selecting aw in association with st
is increased. Similarly an et < 0 means that the selected
action aw has led to a state with an evaluation smaller
than the average, so its probability is decreased. Formally, the change
of the probability is done by updating the weights of the neural unit correspondent
to aw (and only this) as follows:
(6) wwi
= 
etyi
where is
a learning rate, set to 0.01 in the simulation.
In the simulation the evaluator and the actor are trained simultaneously. The evaluator learns to evaluate the states of the world on the basis of the action-selection policy currently adopted by the actor, and the actor learns to improve the action-selection policy by increasing the probabilities of those actions that positively surprise the evaluator, i.e. that produce better results than the actions previously selected in the same conditions.
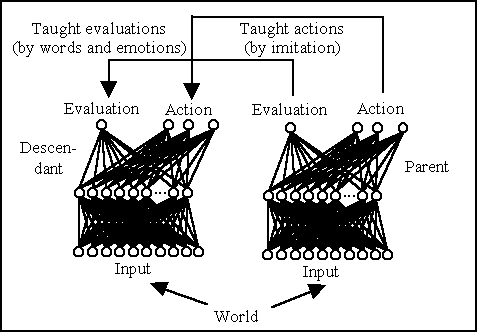
Figure 4: Transmission of evaluations through words and emotions,
and transmission of behaviour through imitation.
The second type of cultural transmission involves the transmission of
"guiding criteria", in this case the evaluations associated by the parent
to the states of the world (figure 4). A parent should
be thought of as verbally (or emotionally) expressing the evaluation that
it associates to the perceived situation and the descendant as learning
by listening (or observing). This is implemented by training the descendant's
evaluator network with a Widrow-Hoff algorithm (with learning rate 0.01)
that uses as output the evaluation that the descendant assigns to the current
perceived situation (V'[st]),
and as teaching input the parent's evaluation.
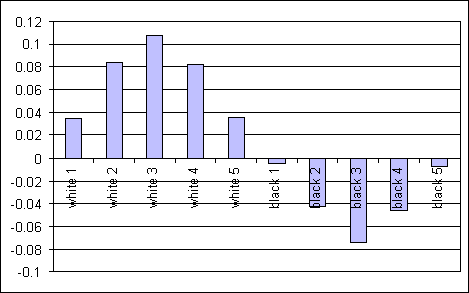
Figure 5: Average (over 20 agents) evaluation of 10 different
world states, after 20000 cycles of experience.
In order to test the effectiveness of the agents' individual learning process, a simulation where each agent had a very long life (200000 cycles) was run. Figure 6 shows the total number of items of good food, bad food and their difference, collected by the whole population of 50 agents against the number of cycles (the graph plots a moving average over 20000 cycles, and shows the average of three simulations run with different random seeds). This graph and direct observation of agent behaviour shows a good capacity to search for good food and avoid bad food.
The following simulations have been run in order to evaluate the effectiveness
and role of the different kinds of cultural transmission (introduced in
section
2) in the population's cultural evolution. Each agent of the first
generation has a life length randomly drawn from the interval [0, 20000].
5000 cycles before its death, each agent generates one descendant to which
it transmits some knowledge (vertical transmission, see Cavalli
Sforza and Feldman, 1981). Each descendant has a life of 20000 plus
a random number of cycles drawn from the interval [-1000, +1000]. Each
descendant has the same neural structure shown previously and a feature
extractor, evaluator and actor with initial random weights. The performance
of the population is measured under four different conditions: transmission
of both behaviour and evaluations; transmission of behaviour; transmission
of evaluations; and no transmission.
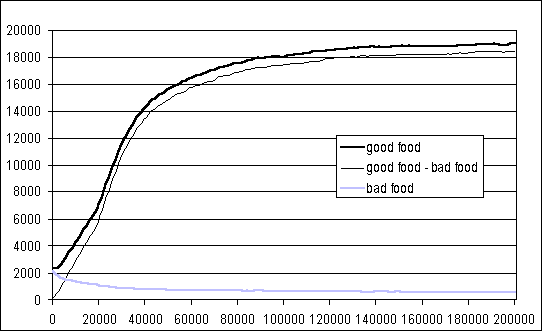
Figure 6: Moving average (20000 cycles) of the items of good
food, bad food, and their difference, collected by the whole population.
Figure 7 reports the results of the simulations
run under these four conditions (for each condition three simulations with
different random seeds were run and averaged). It also reports the plot
of figure 6 relative to one organism with a long life.
This case can be considered equivalent to a hypothetical situation ("ideal
transmission of knowledge") where the cultural transmission from parent
to descendant does not include any loss of knowledge due to errors of imitation
or communication. In the simulations these errors are reproduced by the
fact that the Widrow-Hoff algorithm never brings the error to 0.
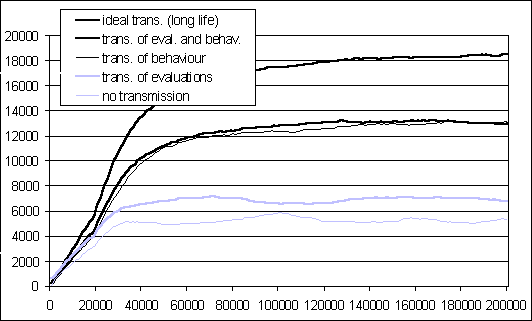
Figure 7: Amount of good food minus bad food collected by the
population in the last 20000 cycles.
Three relevant facts are identified through these simulations. The first is that all the three conditions with cultural transmission (transmission of both behaviour and evaluations, transmission of behaviour, and transmission of evaluations) yield a better performance of the whole population (about 13000, 13000, and 7000 respectively) than the condition where only individual learning is present (about 5000). This means that there is an accumulation of knowledge within the population across the generations: cultural evolution is taking place.
The second interesting fact is that even the most favourable cultural
transmission condition (where both behaviour and evaluations are transmitted),
leads to a performance (13000) inferior to the ideal condition (where there
is no loss of cultural knowledge, 18000). This means that the very process
of transmission implies a continuous loss of knowledge that prevents the
population from reaching the maximum performance. As mentioned, this is
due to the fact that the Widrow-Hoff rule never reduces the error to 0.
It is also due to the fact that the period of cultural transmission for
each agent is limited in time. A further simulation has shown that the
shorter the cultural training period for each agent, the lower the population
performance level reached in the long term (see figure
8, averaged for three random seeds). This result is attenuated by the
fact that in the simulations cultural transmission has (unrealistically)
no costs.
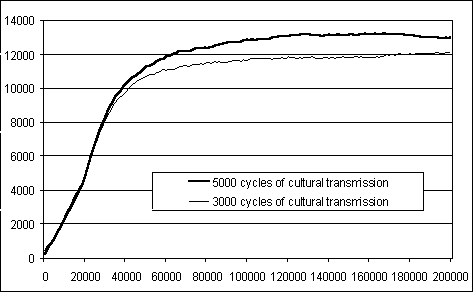
Figure 8: Performance of the population when the cultural transmission
period for each agent is 5000 versus 3000 cycles.
In order to test the interpretation of the first and second facts, another simulation was run with the three distinct cultural-transmission conditions, but with a "synchronised" population: each agent has a life lasting precisely 20000 cycles, first generation included. To reveal changes at a finer time granularity, the performance of the population (determined by the difference between the number of good and bad food items collected), has been measured with a moving average of 1000 cycles (versus 20000 cycles used in the previous simulations; to keep the scale consistency the performance has been multiplied by 20). The results are shown in figure 9 (averaged for 3 random seeds). For clarity the plot relative to the condition with both transmissions of behaviour and evaluations is not reported in the graph because it closely resembles the condition with the transmission of behaviour only.
It can be noted that in both conditions (but in particular with the transmission of behaviour) each new generation, with the exception of the first one, starts its life with skills above the "ignorance" level (i.e. 0). This explains the population's improving performance shown in figure 7, and shows the nature of the cultural evolution process: each newly born agent enters the adult life already possessing some skills. During its life it further improves these skills, and then passes the refined skills to its descendent. The result is an increase of the population average performance across generations.
It can also be seen from figure 9 that at each passage
from one generation to another the performance decays abruptly. This is
due to the errors of transmission of behaviour and evaluations mentioned
before.
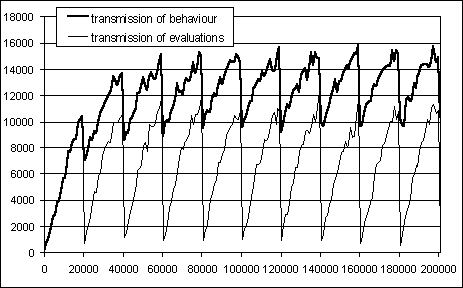
Figuren 9: Performance of the population when the generations
are synchronised.
The third relevant fact that emerges from the simulation reported in
figure
7, quite unexpected, is that cultural transmission of behaviour is
greatly superior to cultural transmission of evaluations (13000 against
7000).
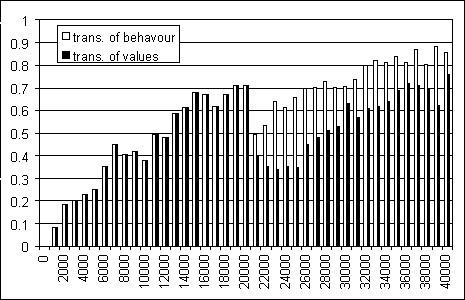
Figure 10: Evaluation assigned to an item of good food perceived
with the central sensor. Average for the population.
Figure 10 explains this finding by showing the dynamics of the evaluations of the first and second generations (20000+20000 cycles) of the preceding simulation. Every 1000 cycles the evaluation that each agent has assigned to the last item of good food seen with the white central sensor (all the other sensors being off) is measured and an average is computed for the population. This evaluation can be considered as an indicator of the overall capacity to evaluate. In fact good food in a frontal position is highly promising of reward and deserves a high positive evaluation. So an agent that has learned to evaluate correctly the states of the world should express a high evaluation in this circumstance.
The most surprising fact is that the second generation's capacity to give correct evaluations at the beginning of life (cycle 21000), is higher with the transmission of behaviour than with the transmission of evaluations (0.5 versus 0.4). The possible explanation of this fact is that once the descendants have culturally inherited the behaviour that leads to search for good food and avoid bad food, they rapidly learn the evaluations by individual experience. The graph shows that after 7000 cycles (cycle 27000) the descendants have already learned to express evaluations similar to the parents' ones, and even improve on their parent's evaluations. At the level of population's performance this fact renders cultural transmission of behaviour quite effective, as shown in the previous simulations.
Where the descendants inherit the evaluations, they are not capable of directly using them to search for good food and avoid bad food, because they do not posses the behaviour necessary to do so. The immediate consequence is that the evaluations are themselves corrupted (from cycle 20000 to cycle 25000) because they prove to be incorrect: after all, having good food in front of you is not a very promising situation if you are not capable of reaching for it! The long-term consequence is that the descendants recover evaluations similar to the parents' ones only after 16000 cycles (cycle 36000), near the end of their life. At the level of population this causes a severe loss of skills passing from one generation to the other, and this makes the process of cultural transmission of evaluations quite ineffective, as shown in the previous simulations.
Lin (1992) presents a model (tested within a food-gatherer predator grid world) where a reinforcement learning agent learns from its own recent past experience ("experience replay") by being (re-) exposed to histories of quadruples of the type "state-action-next state-reward" suitably stored in a buffer. This increases the speed of learning. This model is relevant for social learning because the "experience" could potentially derive from another agent. Tan (1993) presents a model (tested within scout-hunter/co-operative hunters grid worlds) where reinforcement learning agents communicate perceptions or use and update the same policy, so obtaining advantages in terms of speed of learning and performance. Clouse (1996) presents a model (tested using the Race Track game) where a reinforcement learning agent can execute an action "suggested" by an expert teacher instead of its own action. It is shown that higher rates of learning are obtained with high probabilities of suggestion per step. Finally Price and Boutilier (1999) present a model (tested with grid-maze tasks) of "implicit imitation". Here a reinforcement learning agent observes the effects produced by actions executed by a mentor, uses them to build a model of the world (state transitions induced by the mentor's actions), and then trains itself to act by using this model (model-based reinforcement learning).
All these models use a form of "greedy policy" to select actions. This implies that the action to be executed is directly selected as the one with the highest expected (cumulated discounted) future reward. No merits or probabilities are explicitly stored for the selection of actions. In contrast, this storage takes place in the actor-critic model adopted in this paper, and appears to happen in real organisms (Houk et al., 1995). In the research presented here it has been the adoption of a model which includes explicitly stored merits that has allowed separation of the modification of the evaluations from the modification of behaviour, and the investigation of their relationship.
This work has considered only a few forms of guiding criteria, namely reinforcement and the evaluations originating from reinforcement. These have a biological origin, and have been generated (or the mechanisms that generates them has been generated) by natural selection because they enhance organisms' fitness. Other forms of guiding criteria probably have an origin more strongly related to cultural processes and may eventually counter-act biologically generated criteria. For example, Miceli and Castelfranchi (1999) have investigated a notion of evaluation different from that considered here, related to the cognitive formulation of goals, and the notion of "values" (a special kind of evaluation where the goal is left unspecified). These other kinds of guiding criteria, and their relation with the biological ones, should be the object of investigation in future work.
Boyd R., Richerson P. J. (1985), Culture and the Evolutionary Process, University of Chicago Press, Chicago.
Cavalli-Sforza L. L., Feldman M. W. (1981), Cultural Transmission and Evolution: A quantitative Approach, Princeton University Press, Princeton - NJ.
Clouse A. J. (1996), Learning from an automated training agent, In Weiband G., Sen S. (eds.), Adaptation and Learning in Multi-agent Systems, Springer Verlag, Berlin.
Denaro D., Parisi D. (1996), Cultural evolution in a population of neural networks, In Marinaro M., Tagliaferri R. (eds.), Neural nets: Wirn96, Springer, New York.
Houk C. J., Adams L. J., Barto G. A. (1995), A model of how the basal ganglia generate and use neural signals that predict reinforcement, In Houk C. J., Davis L. J., Beiser G. D. (eds.), Models of Information Processing in the Basal Ganglia, The MIT Press, Cambridge - Mass.
Lieberman A. D. (1993), Learning - Behaviour and Cognition, Brooks / Cole publishing, Pacific Grove - Ca.
Lin L. J. (1992), Self-improving reactive agents based on reinforcement learning, planning and teaching, Machine Learning, Vol. 8, Pp. 293-321.
Miceli M., Castelfranchi C. (1999), The Role of Evaluation in Cognition and Social Interaction, In Dautenhahn K. (ed.), Human Cognition and Social Agent Technology, John Benjamins, Amsterdam.
Price B., Boutilier C. (1999), Implicit imitation in multi-agent reinforcement learning, ICML'99 - International Conference on Machine Learning, Pp. 325-334.
Rolls E. (1999), Brain and Emotion, Oxford University Press, Oxford.
Sutton R. S., Barto A. G. (1998), Reinforcement Learning: An Introduction, The MIT Press, Cambridge - Mass.
Tan M. (1993), Multi-agent reinforcement learning: Independent vs. cooperative agents, ICML'93 - International Conference on Machine Learning, Pp. 330-337.
Widrow B., Hoff M. E. (1960), Adaptive switching
circuits, IRE WESCON Convention Record, Part IV, Pp 96-104.