Modeling R&D Strategy as a Network Search Problem
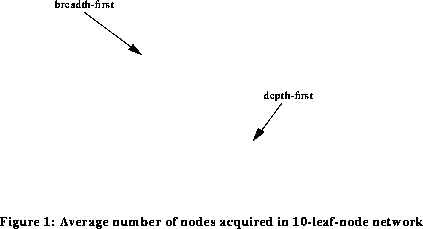
In terms of the number of nodes acquired, it is clear from these experiments that breadth-first search was always much the most successful. The results are shown in Figures 2 and 3.

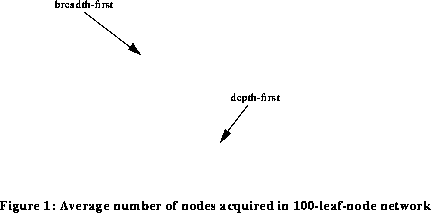
In the representation of the relatively specific technology (10 leaf nodes), the breadth first search was still turning up additional nodes at the end of 50 periods and had reached more than 270 nodes acquired on average among breadth-first searchers. In the same simulation, depth-first searchers had acquired on average about 50 nodes and continued productivity increases were relatively small. In the 100-leaf-node representation, both breadth- and depth-first searches had turned up fewer nodes in the first 50 periods (360+ and 30 nodes, respectively, on average) but the dominance of breadth-first search over depth-first search on the criterion of nodes acquired was much the same.
Certainly one reason for the apparently poor performance of the depth-first search strategy is that it finds root nodes much earlier than does the breadth-first strategy and these offer no scope for further node acquisitions -- they are in effect at the limits of the technological regime.
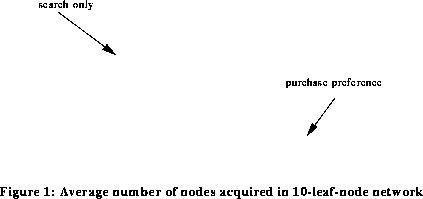
The results reported in Figures 4 and 5 indicate that, in this setup, the largest number of nodes by an order of magnitude or more will be acquired in either technological regime by the agents that search for technology rather than buying it in. This result must stem in some measure from the restriction on search by the agents who will purchase technology when they can -- they can only acquire by search the children of nodes for which they have already acquired at least one child.
Of course, measures of success are not limited to number of nodes acquired but also to the financial implications of the strategies. In the setup reported here, the financial position of each agent is determined by net sales revenue and expenditure on technology search (or R&D).
We assumed that each agent sells one unit of output each period. The price of a unit of output is always determined by a 10 per cent mark-up on the average unit cost of production of all agents in the simulation. For each agent, the unit cost of production in any period is (1+r)-1 times the unit cost of production in the previous period where r is the sum of the values of the nodes acquired in the previous period. Clearly, agents that acquire fewer nodes will have higher costs of production and therefore less net sales revenue to spend on further node acquisition. In these simulations, we assumed that the technology search budget was always equal to accumulated net revenue less previous expenditures on technology search.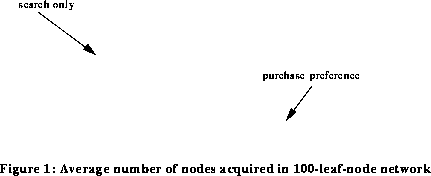
Agents with the highest unit production costs will generate negative net sales revenue. And this is precisely what we observe. On average, agents employing the search-only technology strategy and agents employing the breadth-first search strategy have positive net sales and, therefore, technology search budgets while, after the first few periods, agents buying available technology and engaging in depth-first search have negative technology search budgets so that no search actually takes place. These results are seen in Figures 6 and 7.
Generated with CERN WebMaker