KEYWORDS
Symbiosis, meta-population, multi-patch, cooperation, agent-based simulation, tags, defection.
Abstract.
The paper looks at tag-based cooperation within abstract simulation models. Previous models of this kind have been shown to either have ‘programmed in’ cooperation or to be vulnerable to “strong cheaters”. Previous work by the author included a model of social specialisation and cooperation, but where only a single dominant tag-group arose at any one time and where cooperation eventually collapsed. Here a multi-patch version of this model is explored and show to not to collapse but seed itself indefinitely. Furthermore, the model seems to be resistant to significant levels of strong cheaters.
Introduction
There is a large and growing body of work exploring the necessary and sufficient conditions for cooperation to arise, in particular in terms of the kind of mechanism that might bring this about. The tag approach is one of these. It is a lightweight mechanism that does not require kin selection, memory, or explicit enforcement (by, say, punishment). The idea was introduced by Holland (1993), and has since been explored in a number of variants, including: (Hales 2000; Riolo, Choen and Axelrod 2001; Shutters and Hales 2013).
The idea of a ‘tag’ is that it is an externally observable trait that does not have any ‘hard-wired’ connection with behaviour, but which can be used as a fallible indicator of group membership and hence allow cooperation to develop where otherwise it would not. The basic rule is to cooperate with those with similar tags to one’s own. A key feature of such models is that there is no a priori reason why someone similar is more likely to be trustworthy than anyone else. An obvious social interpretation is the accent and appearance of people – one can (almost always) tell whether someone belongs to your area/type or not. As Hales (2000) pointed out, this mechanism works through the rising and falling of groups with similar tags – although each group is eventually invaded by non-cooperators, destroying the cooperation, an overall high level of cooperation is maintained globally by the constant formation of new cooperative groups (and the dying off of non-cooperative groups).
There are several ways of implementing tag-based mechanisms; each needs a method for representing the tags and a similarity criterion. Hales (2000) uses a simple integer for the tag and the similarity criteria that only agents with identical integers are similar. In the later models of (Hales and Edmonds 2005) tags are only implicitly indicated by network links and agents are similar if they are connected by a link. Here, I follow (Riolo, Choen and Axelrod 2001) and give each agent two floating-point numbers from the interval [0, 1]: one for the tag and one for its tolerance. The similarity criterion is that the difference between another’s tag value and one’s own has to be strictly less than my tolerance value[1]. Thus donation is not necessarily reciprocal – one agent might be within the tolerance of another’s (and hence get donated to) but have a smaller tolerance and not donate back. Agents with a zero tolerance will not donate to any other agent – the possibility of agents adapting zero tolerances is important as it means agents are not ‘forced by design’ to donate to others with exactly the same tag value, as occurs in (Riolo, Choen and Axelrod 2001). This is shown in Figure 1.
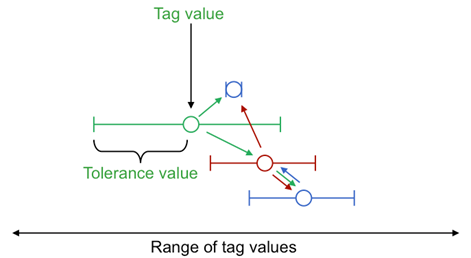
Figure 1. An Illustration Of Tags With Floating-Point Values And Tolerances
In this illustration for each agent the value of the tag is shown as a circle and the tolerance as a range either side of this. The arrows show directions of potential donation. Donation can occur indirectly via a third party. Individuals with zero tolerance only receive donations they do not give.
This method has the advantage that groups are ‘fuzzy’ in definition but can clearly emerge.
The Single Patch Model of Specialists with Tags
In this model (Edmonds 2006), there are a small fixed number of types of nutrient, which all agents need in order to live. The basic premise of the model is that agents are all specialists and can each only produce one of these types. However if they have more than a specified amount they will distribute the excess to others, but only to those who are sufficiently similar to them. Thus in this model (and the multi-patch version) agents have to receive donations of the kinds of nutrient they do not produce in order to survive (and reproduce).
Each agent has the following attributes: its specialist type of nutrition, its tag, its tolerance and the amount of food (of each kind) that it has. Key to understanding this model is its ‘economy’ in terms of food. Food is distributed within the patch divided between the different kinds of nutrition. Each agent gets its share of the kind of nutrition it specialises in. Agents are randomly paired with others within the patch and if (a) it has an excess of a kind of food and (b) a paired agent is sufficiently similar to itself (as described above). During donation the amount of the donation is subtracted from the donor but only a proportion is added to the done (i.e. some is lost)[2]. Each time click a ‘life tax’ of each kind of food is subtracted from each agent and those who have zero of any type die. Those who achieve above a certain level in all kinds reproduce, with a set amount of all of the food kinds being passed to the offspring. Thus individuals continually: appear (arrive or are born), donate, consume resources, (possibly) reproduce, and die (of starvation or old age). The population level is thus variable — determined by the available resources and the efficiency of the sharing structures between them. When agents reproduce, the offspring inherits the characteristics of the parent, but with some chance of mutation occurring to both tag and tolerance values. To get the process started random new agents are introduced to the patch[3]. A more complete description can be found in the appendix of (Edmonds 2006).
This is enough for cooperative tag groups to arise and a short-term burst of cooperation to be established. The whole process can be seen as a life cycle of the tag groups, which although not precisely defined, are obvious when you see them. The cycle goes like this: (1) after a while it happens by chance that a set of individuals with specialisms covering all the nutrient types and whose tag + tolerance values allow them to mutually donate so that all get the nutrient types that they need to thrive, (2) this tag group grows quickly in terms of numbers, (3) a sub-population of these evolves with a smaller tolerance value so these essentially parasitize on the group, receiving donations but not giving them – this causes a kind of predator-prey kind of dynamic (4) finally the parasites dominate and ‘kill off’ the group and the model enters an unviable period. The persistence of stage (3) is important as it allows the group to tolerate the presence of non-cooperators for a while.
This process is illustrated in Figure 2 below. In this figure each line shows the population of individuals specialising in each of the kinds of nutrients. Different phases are evident: UV an un-viable phase where individuals enter the simulation but quickly ‘die off’, CE a phase of cooperative existence where a group of mutually donating individuals forms and thrives, and PP where predator-prey type dynamics arise and eventually destroy the group.
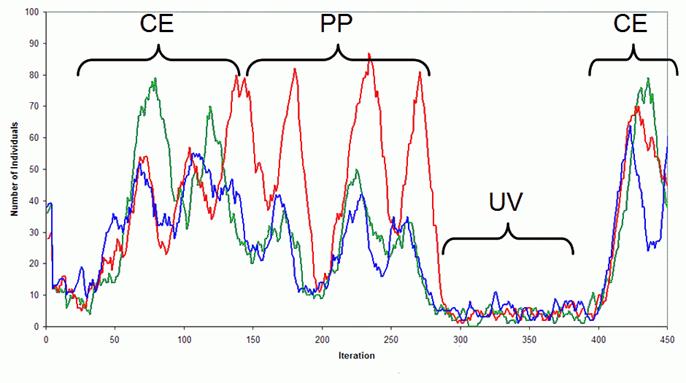
Figure 2. Typical Intra-Population Dynamics Within The Single Patch Model
In earlier versions of this model it was found that some individuals built up huge stores and lived indefinitely, reproducing many times. It was felt that this was unrealistic and so maximum store sizes (for each nutrition kind) and maximum ages (after which agents die and their stores are lost) were introduced to make the task of establishing cooperation more challenging. Not that in this model, without a constant ‘re-seeding’ of new agents the population collapses to unviability, even without any strong cheaters.
Different Kinds of Cheater
Simulation models that explore cooperation have, at least since sought to show how cooperation can persist when non-cooperators can arise or invade and where individual can adapt. The problem is that in the short term it is in the interest of individuals to adapt and stop cooperating and gain the benefit of the cooperators aroun d and not suffer the cost of cooperation themselves, even though they could gain more in the longer term by cooperating if others do the same. The engineering problem is to design a system such that cooperation is not built in, but can arise and ‘mend’ itself flexibly, but that it is as resistant as possible to uncooperative agents.
Of course, what counts as not “building in” cooperation and what counts as a “cheater” to test the system is a matter of definition. Shutters and Hales (2013) look at different ‘strengths’ of “cheaters” and examine a range of models to see which are resistant to which kinds. They define “weak cheaters” as
…agents that may evolve a tolerance so low that they do not donate to any other agent but will likely receive donations. However, these agents still have a trait for tolerance and the mechanism for altruistically donating. If mutation drives the tolerance of a weak cheater back to a positive value, it may resume altruistic behavior. (para. 4.2)
Several of the model versions they explored were resistant to weak cheaters. However they also defined “strong cheaters” as
… agents that have no ability to donate and thus no tolerance trait. They simply display a tag and reap the rewards of displaying that tag to altruistic donors. There is no possibility of a mutation in tolerance causing a return to altruistic behavior because they have no capacity for such behavior and thus – they effectively have no tolerance trait. (para. 4.3)
These are implemented by adding an extra property that indicates being a strong cheater, which when activated stops all cooperation in them or their offspring[4]. None of the models investigated in0 were able to maintain high levels of cooperation when there such agents could arise. The single patch version of the model described above did not ‘need’ strong cheaters to destroy cooperation, since cooperation collapses after a while with only its own internal “weak cheaters”, which naturally evolve within it. Adding strong cheaters into the single patch version of the model does not radically change this, but does somewhat complicate the internal population dynamics – sometimes their introduction acts to kill the group quicker but sometimes it extends its lifetime by predating on otherwise parasitical sub-populations.
The Multi-Patch Model of Specialists with Tags
This version of the model is composed of a 2D grid of connected patches, with the same dynamics of the single patch model within each of these patches, but with three changes:
(1) a (low) probability of migration between neighbouring patches (those that share an edge), so that each individual in each time click has a given probability of being relocated to an adjacent patch;
(2) a probability that in any creation of new individuals (via random introduction or reproduction) they are set as strong cheaters (this requires the introduction of an extra Boolean “strong-cheater” attribute to agents that is passed down to offspring);
(3) the introduction of random new individuals is restricted to the start of the simulation and stops after a viable population (defined by the total population reaching a given threshold) is reached.
The first of these changes (1) is the essential move to a multi-patch version of the model, otherwise the model would be simply a collection of independent single-patch simulations. The introduction of (2) allows us to test the multi-patch model with strong cheaters. (3) is simply the removal of a ‘kludge’ in the single-patch model that is no longer needed in the multi-patch version (since re-seeding is now endogenised via migration between patches).
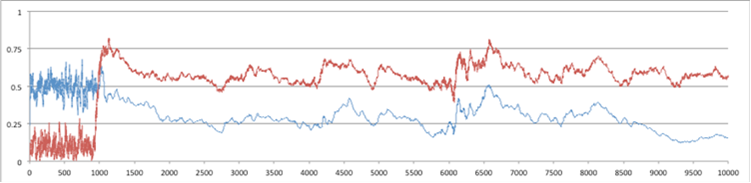
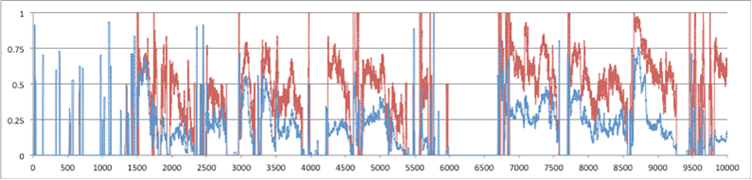
Figure 3. Donation Rates (top line) and Average Tolerance (bottom), both as a proportion of their maximum value, for 10,000 time steps: (above) for the whole 10x10 grid of patches (below) for one specific patch.
With these changes each patch can seed its neighbours with individuals allowing cooperative groups to start afresh in their arms race with both weak and strong cheaters and thus a high level of global cooperation is maintained even though the cooperation always eventually collapses in any one patch, resulting in the demise of individuals there (both co-operators and cheaters).
Figure 3 above shows the donation rate and average tolerance level for a run of 10,000 time steps, the top showing global statistics and the bottom the statistics for a particular patch. Figure 4 below is for the same run but for numbers of individuals: the top graph for total number and number of cheaters, the bottom for number of cheaters and each skill type in the same particular patch as graphed in Figure 3.
I hypothesise that the robustness of the set-up to strong cheaters is due to: (a) when a new cooperative group starts on a patch it is likely to be composed of only co-operators, thus they have a chance to get established before cheaters arrive, (b) as was shown in the single patch model patches have some resistance to cheaters (both weak and strong) due to the internal predator-prey dynamics that occurs and (c) the multi-patch setup allows group-level selection to occur, with cheaters eventually killing themselves due to destroying the efficacy of the group they rely on. However the relative importance of these is yet to be established.
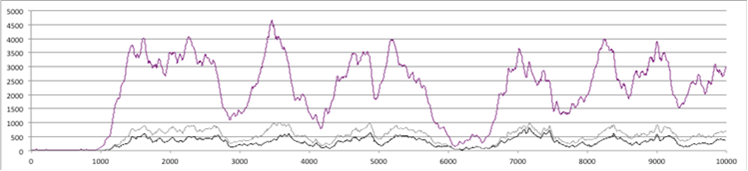
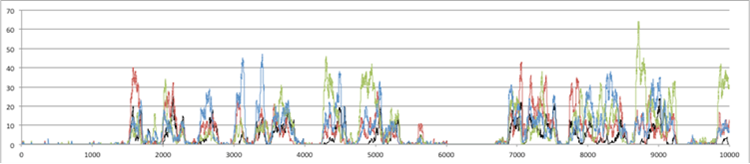
Figure 4. Number of Individuals over 10,000 time steps (above) for the whole 10x10 grid: purple=total population, grey=weak+strong cheaters, black=strong cheaters (below) for a particular patch: top line=individuals with skill 1, bottom= those with skill 2, blue=with skill 3, black=strong cheaters.
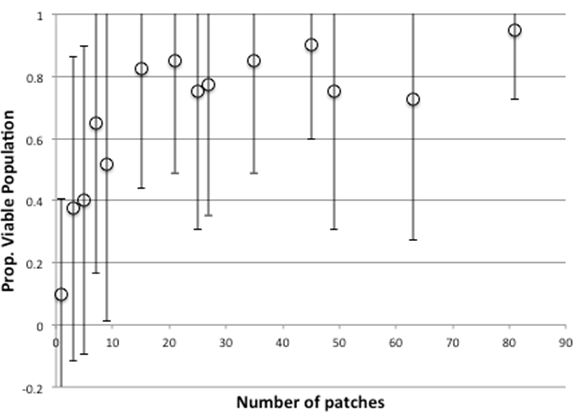
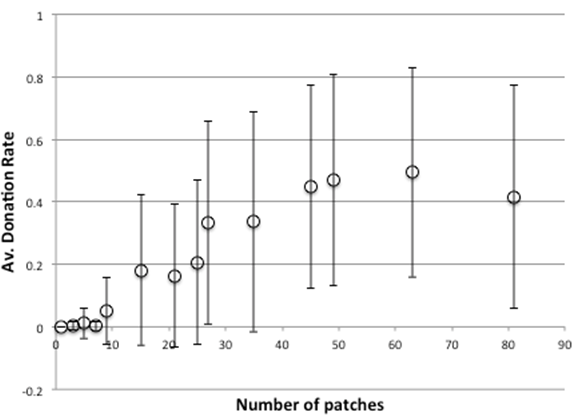
Figure 5. Proportion Of Times There Is A Viable Population After 4000 Time Clicks With Sizes Of Grid, Without Strong Cheaters (0% Probability)
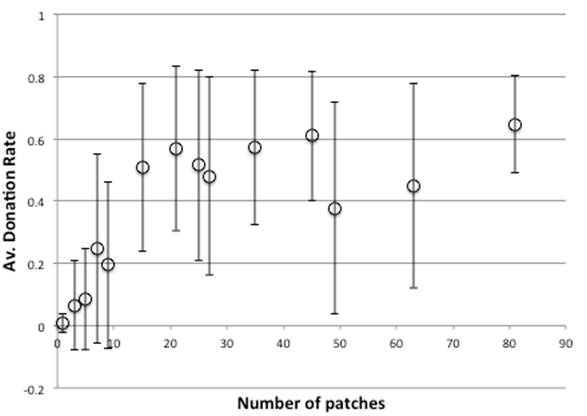
Figure 6. Average Donation Rate After 4000 Time Clicks With Sizes Of Grid, Without Strong Cheaters (0% Probability, Bars Indicate 1SD)
Figure 5 and 6 above shows statistics over the last 1000 time steps (out of 5000) over 20 runs for the multi-patch model, with different sized grids: Figure 53 shows the proportion of runs in which the simulation is viable with different numbers of patches, with Figure 6 showing the average donation rates (both as a proportion of the maximum possible). As the number of patches increase, so does the donation rate and viability, with little increase after a size of 16 patches.
When we introduce a 1% rate of cheater entry into the model (out of new individuals born) the picture is similar, with a delayed plateau starting at 45 patches and slightly depressed levels of viability and donation (Figure 7 & 8). Thus strong cheaters do take their toll, draining the system of some resources and making the whole system less efficient but this is often not a critical one.
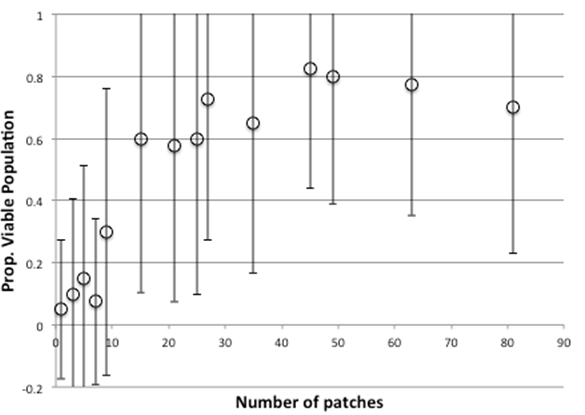
Figure 7. Proportion Of Times There Is A Viable Population After 4000 Time Clicks With Sizes Of Grid, With Strong Cheaters (1% Probability)
Figure 8. Average Donation Rate After 4000 Time Clicks With Sizes Of Grid, With Strong Cheaters (1% Probability)
On investigation, the response of a multi-patch version of the model to the cheater rate seems to be graceful. The impact of different levels of cheater introduction rate on population size (Figure 9) and donation rates (Figure 10) are shown.
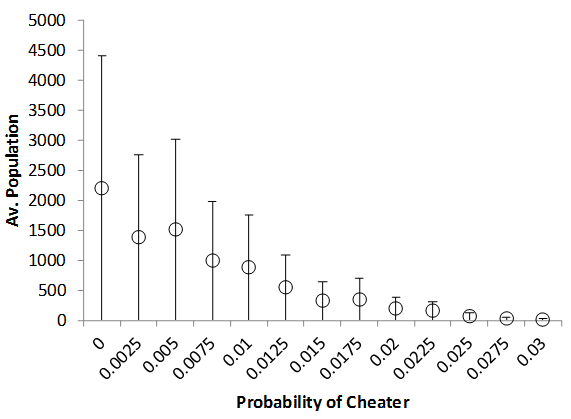
Figure 9. Varying The Rate Of Strong Cheater Introduction On Donation Rate
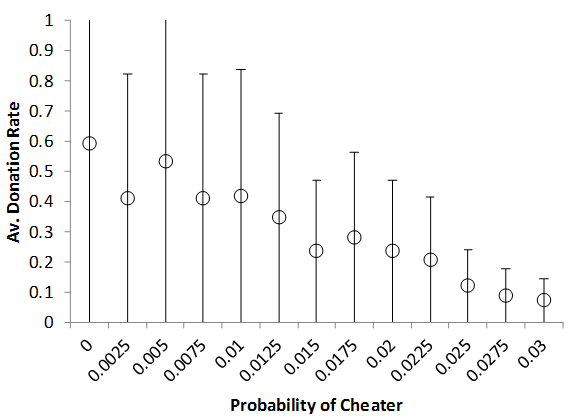
Figure 10. Varying The Rate Strong Cheater Introduction On Average Population Size
Since this is reported in many papers on tag-based cooperation, Figure 11 shows the effect of varying the number of random pairings (opportunities for donation) and the efficiency of donation on the donation rate for runs with a 1% rate of strong cheater introduction (bottom) and without them (top). As with varying the number of patches the presence of strong cheaters means a slightly higher threshold of pairings and donation efficiency occurs and a slightly overall depression of donations rates (which is unsurprising as strong cheaters will not donate).
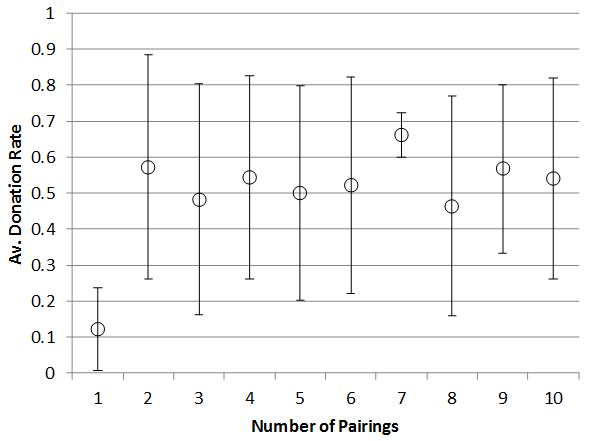
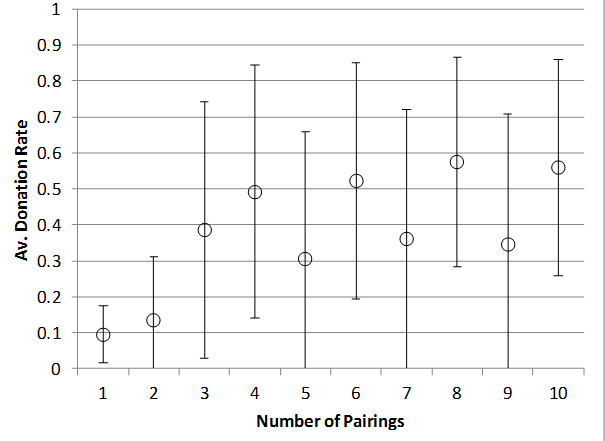
Figure 11. Effect of number of pairings on Donations rate (top) with no strong cheaters, (bottom) with 1% strong cheater rate
Finally, for the record we examine the effects of donation efficiency on donation rates without strong cheaters (top) and with a 1% rate of strong cheaters (bottom). As for varying the number of pairings the effect of having a continual presence of strong cheaters seems to merely require slightly higher numbers of pairings each tick (from 2 to 3) or donation efficiency (from 0.7 to 0.8).
Thus we see that the presence of strong cheaters does degrade the level of cooperation and their presence does require slightly higher levels of parameters that promote the onset of cooperation, but the effect is (a) gradual (Figure 10) and (b) for small but pervasive levels (i.e. a 1% rate) marginal (as in Figures 11 and 12).
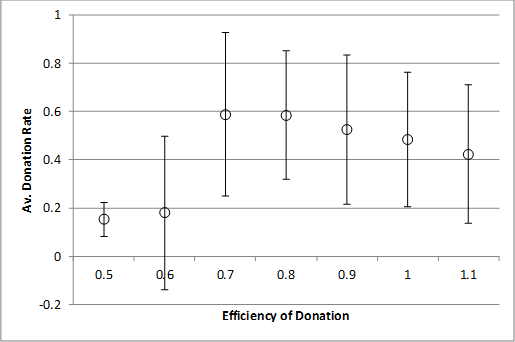
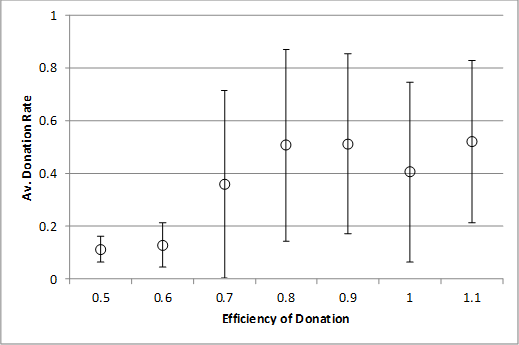
Figure 12. Efficiency of donation against donation rate (top) with no strong cheaters, (bottom) with 1% strong cheater rate
Concluding Discussion
Shutters and Hales (2013) discuss ways that might defeat strong cheaters. The second of which was
… through multi-level selection, in which populations of agents compete against other populations for survival… Those populations that can internally regulate or eliminate non-donors typically displace populations that cannot… enabling tag-mediated altruism to persist dynamically with cheaters in a larger metapopulation. (para. 7.6)
The multi-patch model described here is of this kind. Each patch can host a population and the whole model is a meta-population model. However, there is no displacement of one population by another here, simply the parallel coexistence of populations. Here each population can somewhat resist strong cheaters, but is eventually overwhelmed. When that happens most of the agents in that population die, including the cheaters there – all but the few that happened to migrate. Thus when a population explosion of strong cheaters occurs most of them then die. This is like a parasite that can easily kill its host and hence itself.
Of course, given enough understanding of this (or any model) we could invent a “super-strong cheater” that would defeat this model. There is no ultimate escape from an “arms race” for survival given a sufficiently inventive foe. However, these might not be realistic in the sense that they might not meaningfully correspond to anything observed or potentially existent.
What this does show is that enforcing specialisation along with partial division into sub-populations might help “harden” systems against malicious invasion. The more individuals have to rely on a set of other kinds of skills the more difficult it is to dominate – it is much easier to dominate a monoculture – and the smaller the group in which individuals act, the more the consequences reflect back on that group. Thus the results of this paper and others might follow (Hales and Edmonds 2005) and (Pitt, Schaumeier and Artikis 2012) in applying such biological and socially inspired mechanisms to the design of more robust computational systems, but this will only be a route to reliability if we manage to fully understand the social interaction that underlies these mechanisms.
Acknowledgements
This research was partially supported by the Engineering and Physical Sciences Research Council, grant number EP/H02171X/1.
References
Edmonds, B. (2006) The Emergence of Symbiotic Groups Resulting From Skill-Differentiation and Tags. Journal of Artificial Societies and Social Simulation, 9(1), 10. http://jasss.soc.surrey.ac.uk/9/1/10.html
Edmonds, B., & Hales, D. (2003). Replication, Replication and Replication: Some Hard Lessons from Model Alignment. Journal of Artificial Societies and Social Simulation, 6(4), 11 http://jasss.soc.surrey.ac.uk/6/4/11.html.
Hales, D. (2000). Cooperation without memory or space: Tags, groups and the prisoner's dilemma. In S. Moss & P. Davidsson (Eds.), Multi-Agent-Based Simulation, 1979, 157-166.
Hales, D., & Edmonds, B. (2005). Applying a socially inspired technique (tags) to improve cooperation in P2P networks. IEEE Transactions on Systems Man and Cybernetics Part a-Systems and Humans, 35(3), 385-395.
Holland, J. (1993). The Effect of Labels (Tags) on Social Interactions. Working Paper 93-10-064. Santa Fe Institute. Sante Fe, New Mexico.
Riolo, R. L., Cohen, M. D., & Axelrod, R. (2001). Evolution of cooperation without reciprocity. Nature, 414(6862), 441-443.
Roberts, G., & Sherratt, T. N. (2002). Does similarity breed cooperation? Nature, 418(6897), 499-500.
Shutters, S. T. & Hales, D. (2013) Tag-Mediated Altruism is Contingent on How Cheaters Are Defined. Journal of Artificial Societies and Social Simulation, 16(1), 4 http://jasss.soc.surrey.ac.uk/16/1/4.html.
Appendix
There was not space for a full ODD description of the model
in this paper. However more details, a working version of the model and its
code is at:
http://cfpm.org/models/multi-patch-ecms.html
BRUCE EDMONDS: is Director of the Centre for Policy Modelling and a Senior Research Fellow at the Manchester Metropolitan University. His first degree was in pure mathematics, his PhD in the philosophy of science. He now does a mixture of computer science and sociology. More about him can be discovered via his web page at: http://bruce.edmonds.name