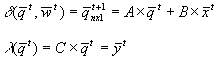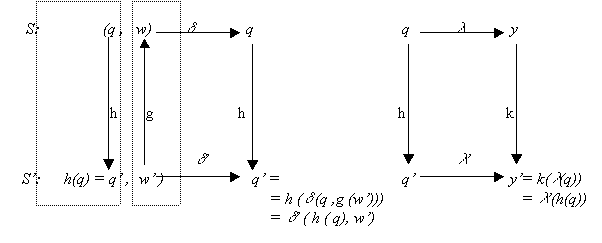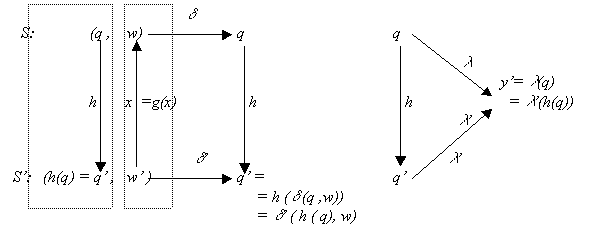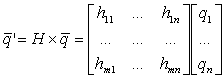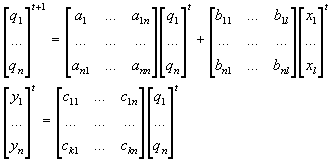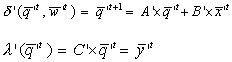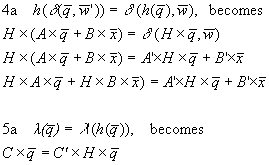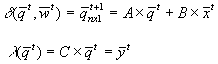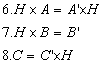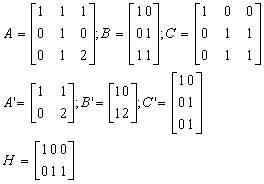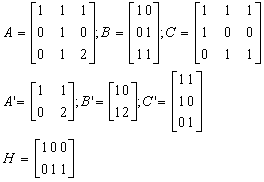Emergent Tendencies in
Multi-Agent-based Simulations
using Constraint-based
Methods to Effect Practical Proofs
over Finite Subsets of
Simulation Outcomes
OSWALDO RAMON TERAN VILLEGAS
A
thesis submitted in partial fulfilment of the requirements of the
Manchester
Metropolitan University for the degree of Doctor of Philosophy
Centre for Policy Modelling
the Manchester Metropolitan
University
2001
Table of Contents
List
of Figures, x
List of Tables, xii
List of Tables, xii
Abstract, xiii
Declaration, xiv
The Author, xv
Acknowledgements, xv
1 Chapter 1 - Introduction 1
1.1 Background, 1
1.2 Aims of the Thesis, 3
1.3 Limitations of the Study, 5
1.4 Outline of the Thesis, 7
2 Chapter 2 - Simulation and Modelling, 9
2.1 Introduction, 9
2.2 Fundamental Notions, 10
2.2.1 Object, 10
2.2.2 System and Process, 10
2.2.3 Subject, 11
2.2.4 Agent, 12
2.2.5 Model, 13
2.2.6 Synthesis, 13
2.3 Zeigler’s Formal Representation of
a System, 14
2.3.1 Zeigler’s Levels of Specification
of Systems, 16
2.3.2 Example: MAS-based Simulation, 19
2.3.3 Morphism between Systems.
Simplifying, 19
2.4 Homomorphism and the Idea of
Metarules, 24
2.5 Systems Exhibiting Structural
Change, 26
2.6 Approximation: Loosening the
Morphism Criterion for Validation, Aggregation, and Alignment of Models, 27
2.6.1 In Traditional Simulation, 27
2.6.2 In Simulation of Structural
Change, 32
2.7 Verification and Validation of a
Simulation, 33
2.8 Event-Driven Simulation, 33
2.9 Simulation of Systems with Variable
Structure, 34
2.10 Towards Alternative Methods for
Analysing the Dynamics of Simulations of Complex Systems, 37
3 Chapter 3 - Proving Theorems in Computational
Models, 40
3.1 Introduction, 40
3.2 Proving: an Ancient Problem, 42
3.2.1 Basic Concepts and (Logical) Model
Search/Construction, 44
3.3 Simulation, Logic-programming, and
Theorem-proving, 45
3.4 Seminal Work: Towards a Procedure
for Checking Unsatisfiability of a Set of Clauses in First-Order Logic, 48
3.4.1 Interpretations, 49
3.4.2 Herbrand Universe and Herbrand’s
Theorem, 49
3.5 Approaches to Theorem-proving:
Syntactic (clausal)- and Semantic (interpretation)-based Searches, 50
3.5.1 Syntactic (clausal)-based
Inference Procedures, 50
3.5.1.1 Robinson’s Principle for First-Order Logic (Chang and
Lee), 51
3.5.1.2 Semantic Resolution, 52
3.5.1.3 Hyperresolution, 53
3.5.1.4 The Set of Support Strategy, 54
3.5.1.5 Linear Resolution, 54
3.5.1.6 Strategies or Heuristics, 55
3.5.1.7 Forward-chaining Search, 58
3.5.2 Semantic (interpretation)-based
Theorem-provers, 59
3.5.2.1 Tableaux, 60
3.5.2.2 Prolog-based Logical Models, 62
3.6 Classification of Theorem-provers, 63
3.6.1 Criteria, 63
3.6.2 Bonacina’s Taxonomy of
Theorem-prover Strategies, 64
3.6.3 Additional Considerations about
Bonacina’s Taxonomy: Classifying Generation of Trajectories in a Simulation, 65
3.7 Constraint-based Search, 66
3.8 Meta-Level Reasoning and Proving
Tendencies, 68
4 Chapter 4 - Understanding Phenomena and
Simulation Dynamics, 69
4.1 Introduction, 69
4.2 Subject’s Bounded Rationality and
the Subject-Object Dichotomy, 70
4.3 Objective Causes of Complexity:
Levels of Complex Systems, 73
4.3.1 Level 1: Matter, Inanimate
Systems, 76
4.3.2 Level 2: Adaptive Systems: Living
Organisms, 76
4.3.3 Level 3: Self-aware Systems or
Systems able to Reason, 78
4.3.4 Level 4: The Level of Meta-beings, 80
4.4 Subjective Notion of Complexity, 81
4.5 Emergent Tendencies, 82
4.5.1 Objectivistic Notion of Emergence
of Tendencies, 82
4.5.2 Subjectivist Notion of Emergence
of Tendencies, 83
4.5.3 Emergence of Tendencies: a
Trade-off between Subjective and Objective Factors, 88
4.6 Tendencies in a Simulation, 88
5 Chapter 5 - Mapping the Envelope of
Simulation Trajectories via a Constraint-based Exploration, 89
5.1 Introduction, 89
5.2 Factors Driving the Dynamics of a
Simulation, 91
5.3 Enveloping Outputs in Simulation
Trajectories, 91
5.4 (Logical) Model-Constrained
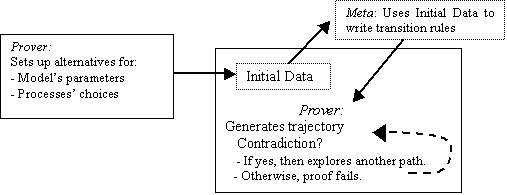
Exploration of Simulation Trajectories, 95
5.5 (Logical) Model Exploration for
Proving the Necessity of a Tendency, 96
5.6 Modeller Beliefs and Proving a
Tendency, 100
5.6.1 A Review of the Concepts of
Explaining, Understanding, and Proving, 100
5.6.2 A Proof of a Tendency in a
Simulation Theory and a Subject’s, Knowledge 103
5.6.3 Interaction between a Subject’s
Cognitive Model and a Simulation Model, 103
5.7 Sources of Constraints: Bounds of
the Searched Space of Trajectories, 105
5.8 Towards an Efficient
Constraint-based Search in MAS: Transformation of MAS into (Logical) Model
Constraint-based Models, 105
5.9 Implementation of a Method for a
Constraint-based Search of Tendencies in MAS, 107
5.9.1 Using SDML and Declarative
Programming Paradigm, 107
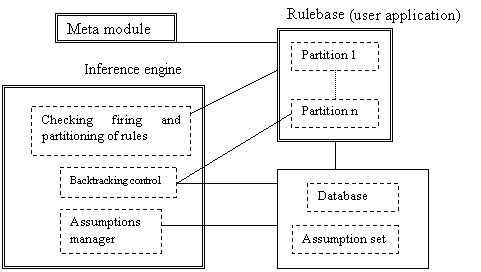
5.9.2 SDML’s Inference Mechanism, 108
5.9.3 An Efficient Translation of a
MAS-based Model into a Single Database-Rulebase (DB-RB) Pair, 118
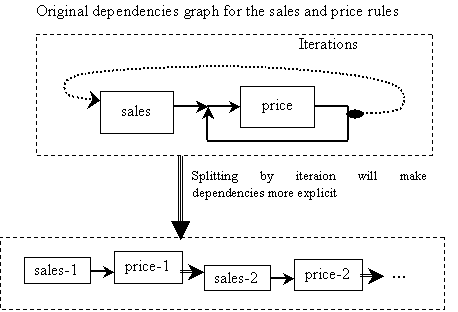
5.9.3.1 First Step. Revealing Dependencies, 118
5.9.3.2 A Problem Appears: The Growth of the Space of Searched
Data, 121
5.9.3.3 Dealing with this Difficulty: Unwrapping the Rules, 122
5.9.4 Overview of the System, 124
5.9.5 Speeding up of the
Simulation, 125
5.10 Morphism and Valid Translation of
Simulation Models, 125
5.10.1 Translating a MAS-based Model into a
(Logical) Model Constraint-based Model, 125
5.10.2 Translating Models from an
Architecture Offering a (Logical) Model-based Exploration into other
Architecture Characterised by a Syntactic-based Exploration, 127
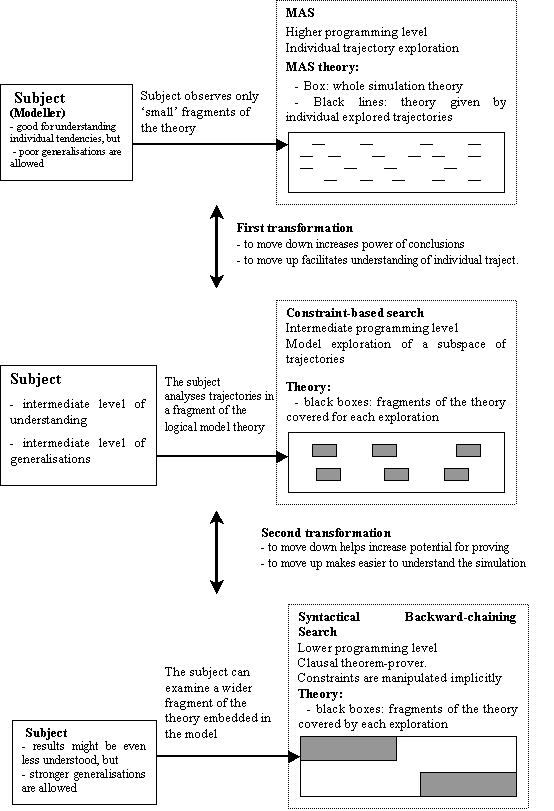
6 Chapter 6 - Transforming MAS to Improve
Efficiency of Constraint Logic-programming, 129
6.1 Introduction: A Hierarchy of MAS
Architectures, 129
6.2 Programming and Experimenting in
MAS to Gain Advantage of High-Level Simulation Paradigm – Higher Architectural
Level, 131
6.3 Translation to Constraint-based Paradigm
for Systematic Exploration of Possible Logical Models – Intermediate
Architectural Level, 131
6.4 Possible further Translation for
Attempting Syntactic Proofs – Lower Architectural Level, 132
6.4.1 Comparing the Architectures, 134
6.5 Modelling Process using
Architectural Transformations, 135
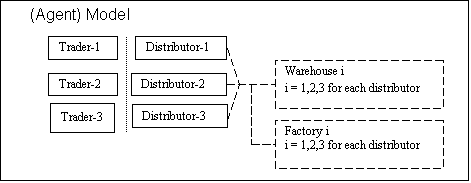
7 Chapter 7 - A Case Study: A Simple
Trader-Distributor Model, 137
7.1 Introduction, 137
7.2 MAS Model using the Strictly
Declarative Simulation Language (SDML), 139
7.2.1 List of the Most Relevant
Predicates used in the Model, 140
7.2.2 Outline of the Most Relevant Rules
used in the Model, 142
7.3 Exploration of Simulation
Trajectories using the MAS-based (Simulation) Model, 147
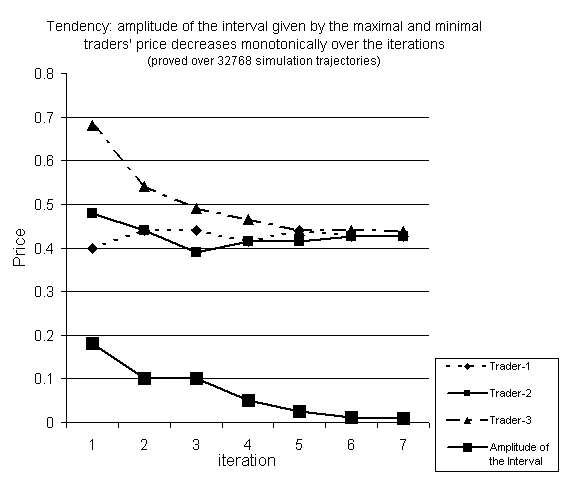
7.4 Envelopes of a Tendency in a
Subspace of the Simulation Trajectories, 148
7.5 A First Attempt to Prove in OTTER, 149
7.6 Facilities for Proving Tendencies
into SDML, 152
7.7 A first Attempt to Prove in SDML:
Resembling the Experiments in OTTER, 152
7.8 Drawbacks of this Implementation: A
More Efficient Implementation is Needed, 153
7.9 An Efficient Implementation in
SDML: a (Logical) Model Constraint-based Architecture, 153
7.9.1 Towards an Automatic Translation
of a MAS-based Model into a Constraint-based Model, 154
7.10 Comparing the Traditional and the
Efficient MAS-based Implementations, 155
7.11 Proving Necessity and Understanding
of an Emergent Tendency, 156
7.12 Comparison with other Approaches, 159
7.12.1 Theorem-provers: OTTER, 159
7.12.2 Proving in MAS: DESIRE, 160
7.12.3 Constraint Logic-programming, 160
7.12.4 MetateM, 161
8 Chapter 8 - Some Implications of this
Research, 163
8.1 Introduction, 163
8.2 Discussion about the Conditions of
how this Thesis works in relation to other Methods, 164
8.2.1 How this Methodology would work in
Simulation Platforms Different from SDML, 164
8.2.2 How Realistic is it to Implement
an Automatic Platform for Translating and Proving Tendencies in a Simulation
Model at Present?, 164
8.2.3 Trade-off between Complexity and
Usefulness of the Techniques Proposed in this Thesis, 165
8.2.4 Complexity of a Constraint
Exploration of Simulation Trajectories in Some Applications, 166
8.2.4.1 Robot Agents (as different from computational agents), 166
8.2.4.2 ALife and Microsimulation, 166
8.2.4.3 Event-driven Simulation, 167
8.2.5 A More Practical Notion of
Emergence: Considering Subjective Aspects in Addition to the Objective ones, 167
8.2.6 Enveloping Tendencies: A New
Approach for Characterising Simulation Outputs, 168
8.2.7 Enveloping Outputs in Simulations
of Chaotic Systems, 168
8.3 Implications for the Modelling of
Complex Systems, 169
8.4 Implications for the Social
Simulation Community, 170
8.5 Implications for the MAS Community, 172
8.6 Bringing Ideas from other Areas of
Research: The Conception of Emergent Tendencies, 173
8.7 Implications for Policy Analysis, 176
8.8 Proving Tendencies in MAS-based
Models and Constraint Logic-programming, 177
9 Conclusion, 178
9.1 Further Work, 180
10 Appendix 1 – Code of the Programmes, 181
10.1 OTTER Code, 181
10.2 SDML Code, after Unwrapping Rules, 192
10.2.1 Module Model, 192
10.2.2 Module Meta, 209
10.2.3 Module Prover, 218
11 Appendix 2
- Dependency Graphs, 246
11.1 For Module Model (after Splitting), 246
11.2 For Module Meta (after Splitting), 249
11.3 For Module Prover (after Splitting), 250
11.4 For the whole Model before Splitting, 258
12 Appendix 3 - Set of Rules before and after
Splitting, 261
13 Appendix 4 - Runs/Result Tables, 265
14 Appendix 5 - Estimation of Speeding-up Gained
from Unwrapping Rules, 267
15 Appendix 6 - Complexity of the Search, 269
16 Appendix 7 - Mapping the Envelope of Social
Simulation Trajectories, 274
17 Appendix 8 - Determining the Envelope of
Emergent Agent Behaviour via Architectural Transformation, 290
18 References, 305
List of Figures
Figure 2.1. Basic notions in Zeigler’s
formalism: input values x1, x2; system
states q1, q2; output volues y1, y2; output function l; and transition function d, changing initial state q1 into a new state q2, 15
Figure 2.2. Graphic representation of a morphism for example 2.1, 16
Figure 2.3. Graphic representation of a homomorphism, 20
Figure 2.4. Morphism between systems S and S’ under a similar
observation frame, 21
Figure 2.5. Homorphism between systems S
and S’ (likewise A, B, A’, and B’; also H is a real
matrix), 23
Figure 2.6. Graphical representation of several control levels where structural
change takes place, 36
Figure 3.1. Graphic representation of the relation among the concepts: Language,
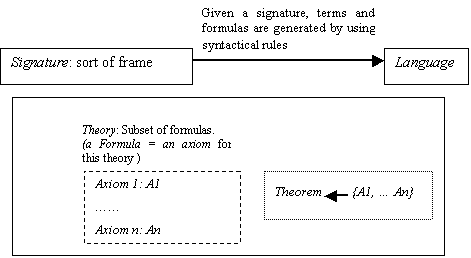
Signature, Theory, Axioms of a theory, and Theorems in a theory, 45
Figure 3.2. A tableau for example 3-6, 61
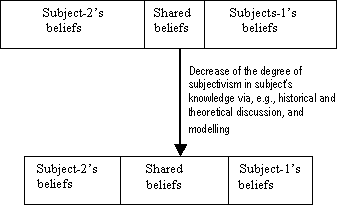
Figure 4.1.Increasing objectivism in subjects’ beliefs, 72
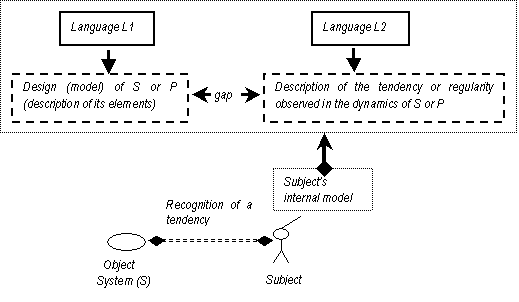
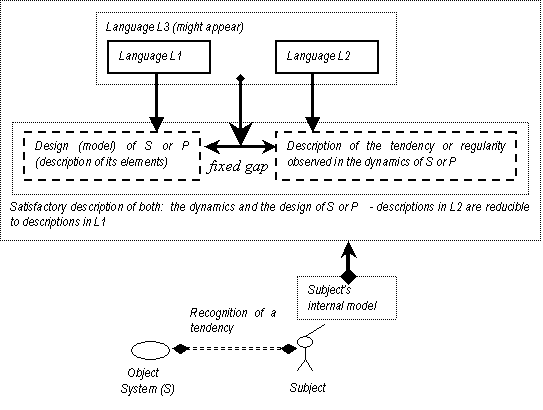
Figure 4.2. Emergence of tendencies for a subject observing a system, 85
Figure 4.3. A new language L3 is used by the subject and the emergent tendency
is no longer considered emergent, 86
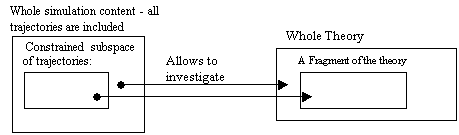
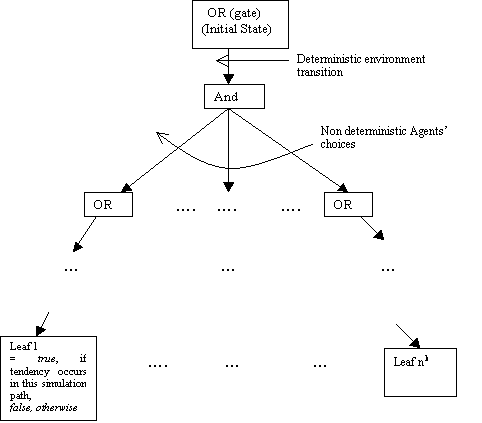
Figure 5.1. Theory given by simulation trajectories, 96
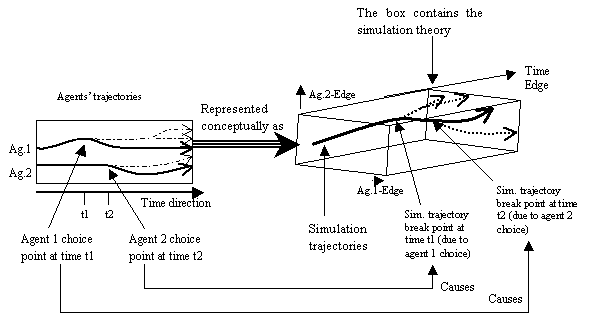
Figure 5.2. Representation of a simulation theory in terms of the simulation
trajectories, and of these in terms of agents’ choices (for a single
parameter-setting and assuming there are two agents), 97
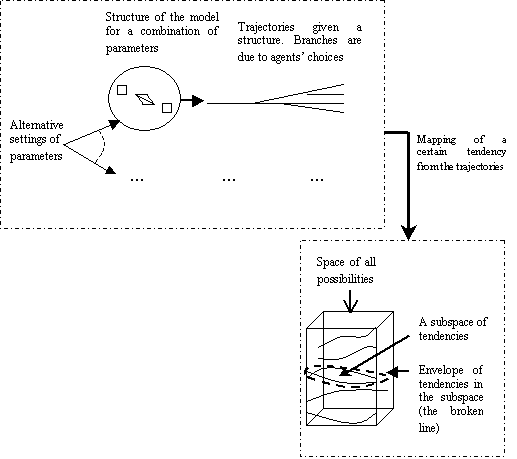
Figure 5.3. A model constraint-based exploration of the dynamics of a simulation, 98
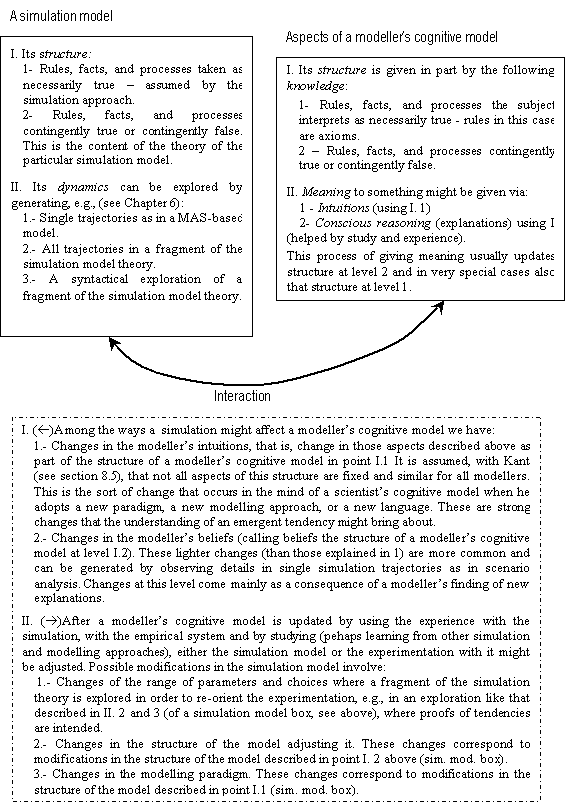
Figure 5.4. Interaction between a subject’s
cognitive model and a simulation model, 104
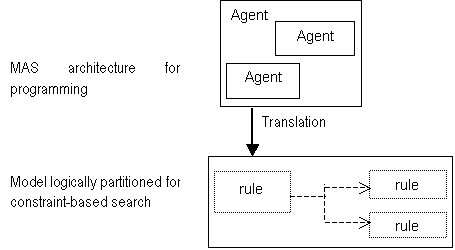
Figure 5.5. Transformation of a MAS into a single
database-rulebase pair, 106
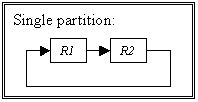
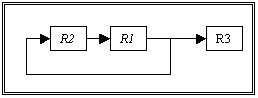
Figure 5.6. Rulebase dependencies for the 2nd example, 111
Figure 5.7. Rulebase dependencies for the 3r example (Case 1), 112
Figure 5.8. Database for the 3r example (Case 1), 113
Figure 5.9. Rulebase dependencies for the 3r example (Case 2), 114
Figure 5.10. Rulebase dependencies for the 3r example (Case 3), 115
Figure 5.11. SDML’s inference mechanism, 117
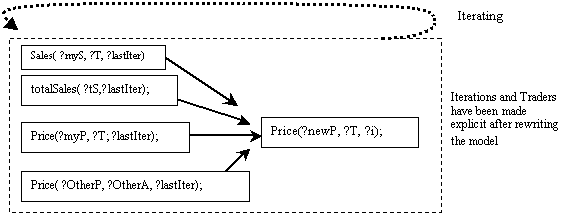
Figure 5.12. Illustrating how agents and time levels become explicit in the new architecture, 119
Figure 5.13. Showing origin of rule dependencies for the rule for prices. Dependencies
are due only to the iterative character of the rule, 120
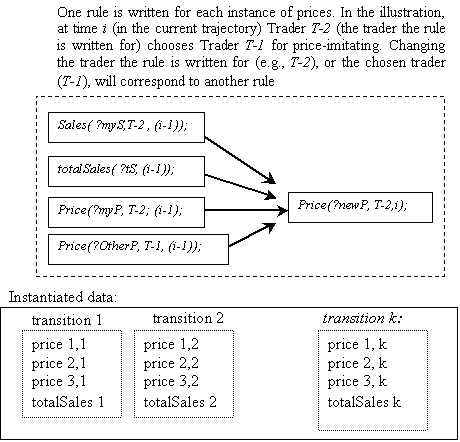
Figure 5.14. Revealing dependencies, e.g.,
agent ?T price-setting at time ?i in accordance with the rule in
the right side of Figure 5.12 (?T and ?lastIter create new
dependencies), 121
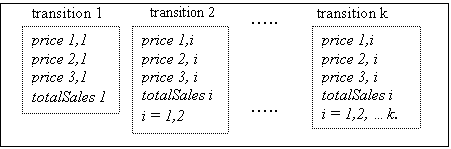
Figure 5.15. The growth of the space of searched data. Notation: price i, j
denotes the price of Trader i at iteration j, 122
Figure 5.16. Splitting of rule for prices, 123
Figure 5.17. Above, ‘unwrapping’ of dependencies is shown. Below, the data-space
searched by the rule-setting for a trader is illustrated, 123
Figure 5.18. Overview of the efficient implementation, 124
Figure 6.1. Sequence of modelling architectures, 130
Figure 6.2. Interactive use of the architectures by a modeller, 136
Figure 7.1. An overview of the model, 140
Figure 7.2.The whole procedure of revealing dependencies and unwrapping rules 154
Figure 7.3. Tendency observed in a
trajectory, 158
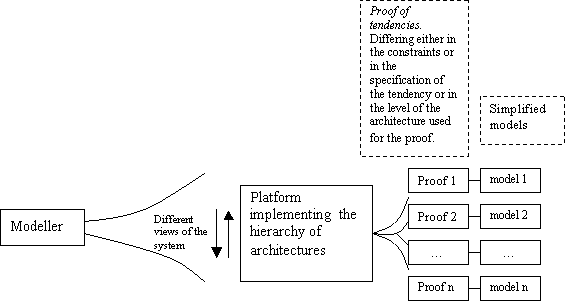
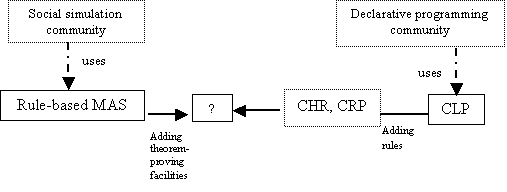
Figure 8.1. The proposed platform for a hierarchy of simulation architectures that
can be used for different purposes, e.g., for generating alternative simplified
models, 171
Figure 8.2. Declarative programming and social simulation communities’ tools, and
recent moves towards common platforms, 177
Figure 15.1. Boolean circuit for the target problem, 270
List of Tables
Table 4.1. A summary of part of Heylighen’s hierarchy of systems’ complexity, 75
Table
6.1. A Comparison of the
Architectures, 134
Table 12.1. Comparing the number of rules in the MAS-based and in the
constraint-based architectures, 264
Table 13.1. Runs/Result Tables, 265
Abstract
This thesis suggests a methodology for
studying complex systems. This method is intended to be particularly useful for
searching and proving tendencies (whether considered emergent or not) in those
systems whose dynamics seem to be strongly dependent on the system’s
components’ interaction (such as social systems). These systems are commonly
simulated in Multi-Agent Systems (MAS).
It begins by examining the formal notions of
simulation, modelling, and theorem-proving. Then it reviews some notions of
complexity and proposes a notion of the emergence of tendencies as based on the
trade-off between subjective and objective factors of complexity. It next moves
on to investigate the dynamics of a system via a platform consisting in a
(logical) model constraint-based exploration of the dynamics of a simulation.
This platform is suggested for systematically exploring the subspace of
simulation trajectories associated with a range of parameters of the model, a
range of choices of the processes (e.g., agents’ choices), and the logic of the
simulation program. Following this, we suggest using this architecture in
addition to the higher architectural level given by a MAS and an even lower
level, a syntactic constraint-based architecture, as complementary means to
investigate aspects of the dynamics of a MAS simulation. The proposed methods
are compared with other approaches for exploring the dynamics of a simulation.
In particular, differences in terms of the notions of morphism among models,
the generality of the conclusions, and the measures of behaviour that each
approach allows are emphasised. In addition, enveloping the simulation outputs
is proposed as an alternative to statistical summaries. This seems to be
especially convenient for studying complex systems and for analysing outputs in
case of applying theorem-proving techniques.
This model constraint-based architecture is
applied to a MAS-based model exemplifying a typical interaction
trader-distributor. A tendency is identified in the MAS-based model and then a
constrained proof is performed in the model constraint-based architecture.
Afterwards, some implications of this thesis for related areas of science are
reviewed. Finally, the appendices include an analysis of the complexity of this
model constraint-based exploration of trajectories and two papers particularly
relevant to the social simulation and the MAS communities.
Declaration
No portion of the work
contained in this thesis has been submitted in support of an application for
another degree or qualification of this or any other university or other
institution of learning.
The Author
The author obtained a first degree in
Systems Engineering at the University of the Andes in Venezuela in 1992. Then
he started lecturing at the Department of Operation Research of the Systems
Engineering School and took a Master in Applied Statistics at the same
University. He is a Member of the Centre for Simulation and Modelling (CESIMO:
Centro de Simulación y Modelado) (http://cesimo.ing.ula.ve/)
of that university. He has some involvement in the areas of Simulation and
Numerical Analysis. His research at CESIMO includes Simulation Methodologies
and Simulation of structural change following Carlos Domingo’s ideas.
Acknowledgements
I would like to thanks my director of
studies, Bruce Edmonds, for his tolerance, patience, and wise guidance; my
supervisor Scott Moss for his assistance and stimulating discussions; and the
other members of the CPM team: Steve Wallis, Juliette Rouchier, Richard Taylor,
and Olivier Barthelemy for their support in many ways. I would also like to
acknowledge the encouragement and assistance received from CESIMO’s members,
especially Giorgio Tonella, Carlos Domingo, and Jacinto Dávila.
Similarly, I would like to thanks CONICIT
(the Venezuelan Governmental Organisation for promoting Science), the
University of Los Andes in Venezuela, and the Faculty of Management and
Business of the Manchester Metropolitan University, for supporting the reserach
reported in this thesis.
For my parents, brothers,
sister, nephews, and for Jasmina.
Computer simulation has been widely
used for studying and understanding systems. It is of particular importance in
the analysis of the dynamics of a simulation. For example, discovering emergent
phenomena and demonstrating their existence in social simulations have been
recognised as key factors in the understanding of social systems (Nigel et
al., 1998; Conte et al., 1997; Edmonds et al., 1998).
Already simulation tools such as Multi-Agent System
(MAS)-based Simulation have proved valuable in the analysis of socio-economic
domains where the agents have bounded rationality (Edmonds et al., 1998; Edmonds, 1999b, 1999c). Different simulation
architectures, methodologies, and techniques have been used in these studies.
Some simulation communities have been interested in studying ‘complex systems’
and ‘composite complex systems’. A MAS-based simulation consists of generating
in a computer the dynamics of a complex system as resulting from the
interaction of simpler agents. The idea is to resemble complex behaviour
observed in empirical systems as the product of the interaction of individuals.
For example, a social modeller might be interested in generating certain
aspects of overall behaviour observed in a society via the interaction of
simple models of individuals (e.g., people).
Now, the social simulation community is going beyond bounded
rationality to explore how ‘social artefacts’, such as roles, norms, and
organisational design, place bounds on social cognition (Carley et al., 1998). This experimentation is
potentially useful, for example: for detecting gaps, inconsistencies, or errors
in organisational theories (Moss, 1998; Axtell, 1996); for providing insight
into organisational behaviour (Carley et al.,
1998); for testing, verifying,
and improving models of artificial social agents (Moss, 1998; Moss et al., 1998a); for investigating the
interdependence between social factors and agents’ cognitive models (Carley et al., 1998), and for aligning models (Mihavics et al., 1996; Axtell, 1996).
Apart from the social simulation community, other examples
of research communities for which studying and analysing the dynamics of the
simulation are important are: ALIFE (Langton, 1989; http://alife.org/), and
microsimulation applications in traffic (Nagel et al., 1998 and 2000).
Usually a MAS-based simulation exhibits very complex
dynamics – in this fact lies its promise but it also means that its analysis
might also be difficult. Behaviour difficult to capture by a modeller but key
for understanding empirical complex systems is resembled in the simulation in
the hope of obtaining hints to improve such an understanding from the
simulation experimentation. Nevertheless, commonly it is still little
understood how such significant dynamics appear from the agents’ interaction.
To develop methodologies for helping in understanding the dynamics of a
MAS-based simulation becomes a crucial task.
As will be seen in Chapter 3, there are two
means by which a modeller can seek to understand the dynamics of computer
simulations: through design and through observation of the dynamics using a post hoc analysis. In MAS, careful
design procedures based on well-understood formal models of agent behaviour can
help a modeller to understand the behaviour of individual agents and, in
special cases, larger parts of MAS. However, understanding the behaviour of
interacting groups of autonomous agents by formal design methods has its
limitations, and even the most carefully designed MAS can exhibit behaviour
unforeseen by its designers as the simulation dynamics become subtle over the
state transitions and large number of data manipulations. Additionally, noted
as factors associated with this difficulty are the facts that systems simulated
in a MAS are of a high level of complexity and that a modeller (in this case,
the observer) has bounded rationality (see Chapter 3). An observer’s bounded
rationality is associated with limited capabilities for capturing and
processing information from the observed system (e.g., the target system or the
simulated one).
Because of this the second way in which a simulation can be
analysed, namely by inspecting the dynamics in a post hoc analysis,
becomes the most used approach for studying MAS. Among the existing
methodologies for doing such post hoc analysis are: scenario analysis
(Domingo et al., 1996b), where one
single MAS trajectory at a time is examined and analysed, and the Monte Carlo
approach (Zeigler, 1976), where the MAS is repeatedly run and statistics are
collected about general trends over a sample of trajectories.
However, neither of these traditional ways of analysing
computer dynamics is satisfactory for MAS-based Simulations (MABS). On the one
hand, it is usually prohibitive in terms of computational resources to explore
all simulation trajectories using single scenario analysis. Moreover, its use
is restricted to certain ‘arbitrarily’ and subjectively chosen trajectories.
Scenario analysis can help by exposing possibilities for the dynamics of the
simulated system. Its value for training the modeller or the policy analyst
about ‘possible future worlds’ has been recognised in simulation applications
related to policy analysis (Axtell et al.,
1996; Wack, 1985; Domingo, 1996b). Nevertheless the fact that arbitrarily
unexplored trajectories are left aside makes difficult the generalisation of
conclusions and the analysis’s application in wider theory.
On the other hand, in Monte Carlo techniques the analysis of
the simulation is made using a sample of the trajectories. Consequently, an
arbitrary (in this case the arbitrariness is random) exploration of
trajectories is also carried out. The use of statistics supports only
probabilistic generalisations but not mathematically (or logically) valid
proofs. Hence the usefulness of these techniques in theoretical applications is
limited - they do not give definitive answers but only probabilistic ones.
Consequently there is a need to advance the search for new
computational methodologies and techniques that allow a more rigorous
exploration of the dynamics of simulations of complex systems.
The main aim of this thesis is to help in
filling the gap apparent in the need for better computational methods for
studying MAS dynamics, as was pointed out in the last section. It is of
particular interest to develop a methodology for proving emergent tendencies in
Multi-Agent Systems. The following sub-goals of the thesis can be stated as
part of an effort for developing methodologies and techniques to help in the
exploration and proof of emergent tendencies in simulation of Multi-Agent
Systems.
o
To develop a methodological approach for exploring and
proving emergent tendencies in computational models
The intention is to show
that it is possible to prove theorems about social simulation models. The idea
is to prove that emergent tendencies are (or are not) general under certain conditions
when varying certain factors of the simulation dynamics. This methodology will
allow a modeller to elaborate conclusions about the behaviour observed in the
dynamics of a simulation theoretically stronger than those that traditional
explorations of simulation trajectories are able to support (e.g., Monte Carlo
techniques permit one to infer only probabilistically valid conclusions; for
more details about traditional approaches and their drawbacks, see Chapter 2
and especially sections 2.6 and 2.10).
o
To develop some techniques for implementing such a
methodology
The purpose is to apply
the methodology in a particular simulation example and to give an indication of
how it could be automatically implemented. Appropriate techniques for
implementing the methodology in a particular simulation language would be
developed. The language SDML for writing MAS is chosen for such implementation
because of the relevance of MAS-based models for studying complex systems in,
e.g., social and economic systems, and because this language is suitable for
implementing formal proofs (e.g., it is a declarative language with a
well-grounded underlying logic). These advantages give SDML advantages over
many other existing simulation languages, where usually only traditional
explorations of simulation trajectories are allowed (e.g., traditional
event-driven simulation languages, e.g, SLAM; see Pritsker, 1995, for more
details with reference to this point; this argument is better explained in
Chapter 2).
o
To investigate the trade-off between complexity and the
usefulness of these techniques
Factors and criteria for
this trade-off will be identified relative to a conception of complexity. This
conception will be strongly linked to a notion of what are considered as
emergent tendencies in complex systems. In addition, the computational
complexity of the task which the approach in this thesis suggests, i.e.,
proving in a computational model, will be investigated and presented (see Appendix 6
- Complexity of the Search). This investigation allows a discussion of the trade-off
between computational complexity and factors related to the usefulness of the
technique. On the other hand, difficulties for implementing the technique and
modelling approach (MAS-based and constraint-based simulation and proving) in a
particular language (SDML) will be examined. Further, how different such
difficulties would be in case of modelling in other simulation languages will
also be discussed. In particular, for analysing simulation outputs, enveloping
of tendencies will be proposed as an alternative to central measures and other
statistical summaries. The idea of using an envelope is to present an
alternative to statistical summarises and to overcome some of their drawbacks
for studying complex systems (for example, that pointed out by Crutchfield,
1992, p. 35; aspects of this trade-off will be discussed in section 8.2).
o
To develop a particular case study
An abstract simulation
based on a ‘need problem’ will be focused upon. The idea is to apply the
developed methodology and techniques in a typical model of an empirical system.
The intention is to use this typical example to show that the developed
methodology and techniques effectively work. Consequently, it must be possible
to arrive at stronger conclusions about behaviour in the dynamics of the model
than those possible when using traditional methods; i.e., conclusions must find
stronger support in the theory of the simulation model than in those allowed by
existing techniques (this case is presented in Chapter 7).
o To
review the conception of emergent tendencies
Conceptions
of emergent phenomena useful for understanding emergent tendencies in
computational models will be reviewed. Of special interest will be criteria for
testing whether certain tendencies can be considered as emergent by an observer
(e.g., by a modeller). The intention is to achieve a more ‘practical’ notion of
the emergence of tendencies, one more practically useful for modelling complex systems.
Existing modelling approaches like those named above as well as modelling in
different areas of research (e.g., in physics) traditionally consider the
emergence of tendencies only from an objectivist point of view. They are
usually linked to objective notions of the complexity of a system. However, it
also seems convenient, especially when modelling certain complex systems such
as human systems, to examine the relevance of subjective factors for a tendency
to be considered as emergent by a modeller. These factors seem to be sourced on
a modeller’s bounded rationality. The idea is to consider both the objective
and subjective factors and to reflect on their trade-off (Chapter 4
is specially dedicated to examining these aspects; a further discussion about
the usefulness of this concept is presented in section 8.2.5).
This thesis is
focused on (and limited to) the computational modelling of computer systems.
The terminology and concepts are intended with respect to this domain. This
bias applies throughout the thesis (except in the discussion in sections 4.2-4.3 and 8.6) and should be held in mind when reading the
discussion involving highly polemical terms such as ‘complexity’ and ‘emergence
of tendencies’.
This thesis is born out of the following disciplines:
Social simulation. This is one of the areas where a need
for better methodologies for analysing and understanding better the dynamics of
computational programs has been identified (Conte et al., 1997; Edmonds et al.,1999).
Multi-agent systems
(MAS), in particular their use for simulation of complex systems conceived
as made up from the interaction of sub-systems with certain autonomy (Weiss,
1999).
Automatic reasoning
and theorem-proving, specifically their application for analysing the
dynamics of computational programs. In the application to be considered in this
thesis, it will be useful for studying the dynamics of simulation programs; in
particular, the interest is in model-based exploration of simulation programs
(Wos, 1988).
Artificial Intelligence.
This discipline of research includes modelling using MAS, Automatic Reasoning,
and other sub-disciplines of research to be assessed in this thesis (Stuart,
1995).
Computational
modelling of complex systems. It
includes areas of research relevant to this thesis, such as modelling of social
systems and, in general, Multi-Agent-based Simulation (Casti, 1992; Holland,
1998). Methodologies to be developed in this thesis will be useful not only in
social systems but also in different sub-areas of computational modelling of
complex systems.
Systems theory, more specifically notions of systems
from an evolutionary perspective, as is conceived by the group working in
Principia Cybernetics at the Center Leo Apostol in Belgium
(http://pespmc1.vub.ac.be/CLEA/). Heylighen’s ideas will be accorded special
importance (Heylighen, 1992 and 2000c; http://pespmc1.vub.ac.be/HEYL.html).
Broadly speaking, the example model will be a
representation of a trader-distributor relationship. However, in order to
facilitate the development of a technique for exploring and proving in the
dynamics of the simulation, a more abstract and limited model will be
considered. The case study to be developed will be typical but not necessarily
representative of a particular empirical system. This will remove unnecessary
time-consuming activities during the research, for example, data collection and
validation of the model. traders and distributors in the model will be
simplified to agents whose main activities are price- and sales-setting, and price-imitating,
in the first case; and order-setting in the second case. It is hoped to apply
this technique in future studies using more elaborate examples.
It is foreseen that the methodology and techniques in this
thesis will be applied to other areas of MAS-based Simulations, especially when
studying complex systems. It is hoped they can be implemented automatically in
some MAS. In order for this to be possible, these systems must have certain
capabilities for exploring computational program dynamics such as those found
in theorem-proving and constraint logic-programming (Moss et al., 1997;
Abdennadher et al., 1995;
Abdennadher, 1999; Frühwirth et al.,
1992; Rainer et al., 1988; Marriott, 1998).
First, in Chapter 2, a review of basic concepts and
the formal aspects of simulation and modelling are presented. We begin by
considering basic concepts in classical systems theory in order to set a first
‘world view’ for the thesis. Then Zeigler’s foundational theory for simulation
and modelling will be examined. Afterwards other aspects of simulation (which
Zeigler’s theory does not consider), such as structural change and modelling in
Multi-Agent Systems, will be considered. Following this, concepts related to
the formal use of simulation results including validation, verification, and
simplification of models are examined. At the end of the chapter, the main
drawbacks of traditional post hoc analysis of simulation outputs for
studying complex systems are pointed out and theorem-proving is suggested as a
promising area for alternative approaches.
Following, in Chapter 3, formal aspects of theorem-proving
are reviewed, including the most common approaches: the model-based (semantic)
approaches and the resolution-based (syntactic) ones. A comparison of these
methods is presented. Chapter 3 also includes references to OTTER as an example
of a successful theorem-prover. Its more relevant characteristics are described
later in the chapter (OTTER is used in the implementation of the case study in Chapter
7).
Chapter 4 offers a review of some conceptions with respect
to understanding simulation dynamics. Special attention is given to the concept
of emergent tendencies. Some definitions of this, using different ideas of
complexity and the notion of bounded rationality, are presented. Special
emphasis is placed on a trade-off between the objective aspects (grounded in an
observed system) and the subjective factors (grounded in an observer’s
language).
Chapters 5 and 6 present a methodological approach to the
study of complex systems using Multi-Agent Systems. Chapter 5 suggests a model
constraint-based exploration of tendencies in a subspace of simulation
trajectories. Compared to existing approaches, this method allows a modeller to
apply stronger notions of morphisms for comparing models, to reach more general
conclusions about the dynamics of a model, and to use other measures of
behaviour than statistical summaries. This chapter also discusses aspects of
how an analysis of the simulation outputs can help a modeller in better
understanding aspects of the simulation and, by extrapolating, of the empirical
system. In addition, it proposes enveloping tendencies as an alternative to
traditional methods for studying simulation outputs. Then, Chapter 6 proposes a
platform consisting of a hierarchy of architectures for understanding MAS-based
models. The platform is: at the first level, the MAS-based model; at the
intermediate level, the model constraint-based architecture proposed in Chapter
5; and, at the lowest level, a syntactic constraint-based architecture. This
platform is intended to assist a modeller in understanding the simulated
complex system by showing complementary aspects of the dynamics of the model.
Chapter 7 offers a case study where the methodology
suggested in Chapter 5 is applied. The model consists of a MAS-based model of a
typical trader-distributor interrelationship.
Chapter 8 discusses some implications of this research in
related areas such of modelling and simulation. It includes a discussion about
how the methodology and techniques developed in the thesis may be implemented
in other platforms and about the trade-off between the usefulness of such
techniques and the complexity of their implementation. Conclusions are offered
in Chapter 9.
Finally, the appendices and a bibliographic review are
presented. Appendices include a review of the speed-up achieved in the case
study when the model is translated from the MAS to the constraint-based
architecture (both in SDML), an examination of the computational complexity of
the search proposed in this constraint-based architecture, and two papers
relevant to the social simulation and MAS research communities.
The aim of this
thesis is to develop tools and a methodology helpful for understanding
simulation of social systems and other complex systems. It is of special
interest to apply such a methodology in the simulation of social systems using
MAS. Given the difficulties for understanding a MAS-based model from its
design, the method commonly used is to inspect the dynamics of the simulation
in a post hoc analysis.
Understanding of a simulation is closely related to
simplification, validation, and alignment of models. They rest in a post hoc
analysis of simulation trajectories, and in a mathematical notion of
homomorphism. Because of the difficulties involved in evaluating the formal
notion of homomorphism in simulation, weaker notions are used in the existing
techniques. As will be seen, to circumvent these difficulties, the idea of approximation
is used instead of that of strict morphism. Among the widely used
techniques based on this notion of approximation are scenario analysis and
Monte Carlo studies. However, as pointed out in the Introduction to this
thesis, they both have serious drawbacks.
It is our intention in this chapter to review existing
formal simulation approaches and the notion of homomorphism used there, in
order to make more explicit the drawbacks of these techniques and then illustrate
the advantages of the approach to be proposed in this thesis. In particular, we
seek to develop a methodology that allows a modeller to prove emergent
tendencies in computer simulation of complex systems. This will lend support to
the implementation of the strongest notion of morphism, more so than the weak
one commonly used in the named existing techniques.
As a starting point, in this chapter basic notions about
simulation and modelling will be presented, to help, as said, in clarifying,
for example, drawbacks in the existing techniques and desirable properties in
alternative techniques. Then, in the next chapter, concepts related to the
proving of theorems in computer models will be reviewed, in order to establish
a background helpful for developing a methodology for proving tendencies in a
simulation. In Chapter 4, before presenting a methodology for proving a theorem
in a simulation in Chapter 5 notions related to the understanding of emergent
tendencies in the dynamics of a simulation will be discussed.
In the first part of this chapter, basic aspects of Systems
Theory will be described as part of the framework (‘world view’) of this thesis
§ 2.1). This will be used throughout the whole thesis, but it will be of
particular value as a basic reference for discussing notions of understanding
and emergence in Chapter 4, where this discussion and the development of a
‘world view’ will be extended. Then, in the second part of the chapter, the
fundamental theoretical aspects of simulation and modelling, starting from
Zeigler’s formalism and progressing to MAS, will be reviewed. In addition,
simplification, integration and alignment of models will be discussed. These
are important considerations when modelling complex systems. Finally, in
section 2.10 some drawbacks of traditional simulation for
modelling complex systems will be discussed.
The
basic notion for the ‘world view’ taken in this thesis will be presented as
understood in classical systems theory (Heylighen, 1992; Ashby, 1964;
Checkland, 1981; Checkland et al.,
1999; Churchman, 1968; Domingo et al., 2000; Fuenmayor, 1986).
The
basic entity identified in reality is called an object. Its basic
characteristics or attributes, e.g., colour, size, are called properties.
In this view,
objects are one of the basic semantic units. This is one of the more basic
notions of object, one widely used in computer science and logic. It is useful
for describing more abstract concepts as made up of objects. However, its value
is quite limited because processes (e.g., evolution) cannot be passively
represented. So, a move towards a higher level of abstraction is necessary in
order to identify a basic entity useful for abstracting and modelling processes.
Such an entity is the system. More elaborated notions of ‘object’ will be
considered in Chapter 4.
In classical
systems theory, a system can be thought of as a kind of object with additional
properties. Among the special attributes a system presents are:
·
A distinction
between the whole, its components, and the interrelations among these
components. A component can be a sub-system (a system in itself) or an object.
For example, consider a model of a trader-distributor-consumer interaction. The
model will represent the whole thing. Among the components are traders,
distributors and consumers, and among the interrelations are orders from
consumers to distributors and from distributors to traders; sales from traders
to distributors and from distributors to consumers; and traders’ and
distributors’ price-settings.
- Overall properties of the system
are different from components’ properties. Such a system’s properties enjoy some degree of independence from
components’ properties since they are difficult to explain apart from
these. For example, among the overall properties of a model such as that
described above are the dynamics of prices. Generally, tendencies about
prices difficult to understand from the individual behaviour of components
(e.g., traders, distributors, and consumers) appear. The term ‘properties’
of a system will be used instead of ‘end’ or ‘purpose’ of a system (as
used in some studies) in order to avoid vagueness in the discussion, as
that is a less polemical concept.
- Dynamical structure, a function
given by some laws of change over time, which specifies a system’s
behaviour. Dynamics introduces the fundamental notion of process. This is
significant as it allows a modeller to describe processes as a system’s
dynamics. For example, the process of evolution as given in nature (a
natural system) has been useful in different areas of research, most
obviously in biology, but also in complex systems such as social systems.
Even more, evolutionary theories have been elaborated in ways that intend
them to be useful for approaching systems in general (Heylighen, 1992).
Considering the example of a trader-distributor-consumer interaction, each
component has a certain behaviour given by its ‘goals’ in that environment
(in such sort of ‘market’). They have certain ‘rules’ for buying, selling,
and price-setting. These give the laws of behaviour of each component.
Certain laws of behaviour of each component plus some additional laws,
such as ‘total distributor sales are equal to total consumer’ purchases’,
are useful for generating behaviour of the whole system. In this example,
the additional rules might be in accordance with ‘marketing theory’ or
might simply have the purpose of achieving ‘consistency’ of the whole
system.
Other notions of systems found in the
literature will be reviewed below.
A subject is defined as a system with a
vicarious mechanism (Heylighen, 1991a). A vicarious mechanism selects among
alternative actions in order to satisfy a particular system’s goal. This goal
might be, e.g., surviving, or perhaps increasing economic benefits. In some
subjects, e.g., human beings, this vicarious mechanism rests on genetics and
internal models. The genetics provide useful information for surviving as they
are passed from individuals to their descendants. This process is actuated for
an internal mechanism, which is out of rational control by the subject. Some
subjects enjoy a second mechanism at a higher level of complexity, internal
models of their environment allowing them to take choices. Some subjects, e.g.,
animals, benefit primarily from the first kind of mechanism. The vicarious
mechanism is important as it allows the system to take actions in advance of
other actions in the environment, in order to adapt in some degree by itself
and decrease the likelihood of risky ‘corrective’ actions from its surroundings
(see section 4.3).
In
this thesis, the term ‘agent’ is used of a kind of system with certain
characteristics. Different notions of agents can be found in the literature.
For example, in researches in biological and social systems, an agent may be
defined as an object with a vicarious mechanism, i.e., a subject; while for
people working in physics, an agent may be any entity able to influence others
in its surroundings. For instance, when studying the solar system, the earth as
a body attracting and rejecting other bodies in the solar system will be an
agent. This notion is shared in some modelling computer programs such as the
simulation language SDML (Moss et al.,
1998a), where an object might be any entity with a rulebase and a database. An
agent in SDML is just an object interacting with other objects or an object
useful for providing the context (environment) where other objects interact.
It seems useful to
check in a dictionary the most common conceptions of agent (Merrier-Webster; http://www.m-w.com/):
Main Entry: agent
Pronunciation: 'A-j&nt
Function: noun
Etymology: Middle English, from Medieval Latin agent-,
agens, from Latin, present participle of agere to drive, lead, act, do; akin to
Old Norse aka to travel in a vehicle, Greek agein to drive, lead
Date: 15th century
1: one that acts or exerts power
2 a: something that produces or is capable of producing an
effect: an active or efficient cause b: a chemically, physically, or
biologically active principle
3: a means or
instrument by which a guiding intelligence achieves a result
Here,
the notion of agent is linked to the notion of influencer. An influencer might
be thought of as an object influencing elements in a broader system, but this
object does not necessarily have to be considered as a component of the system.
While an agent is defined in terms of its actions towards its surroundings, a
sub-system is defined as part of the interacting elements defining a system.
The conception of agent is more closely linked to the idea of an active entity
influencing the environment a subject is studying, but it is not necessarily a
key element for helping a subject’s understanding. On the other hand, a system
is more closely related to the notion of evolving entity, which is of interest
for a subject, as it helps him to model and understand relevant parts of its
surroundings.
In general a model is a
representation of an object (‘realist position’) or of an idea (‘idealist
position’) that a subject has created. In the case of modelling physical
systems, a realistic position is taken
and there will be a relation of correspondence between the original entity in
the environment and the model an agent has elaborated. However, when modelling
social systems, which are of particular interest in this thesis, such a
physical reference is not clear and the modelling process becomes more subtle
as ideas from theoretical and abstract grounds are also appropriate to build
the models. Nevertheless, in any case, a model is considered helpful (in
practical terms) only if it is simpler or at least easier to manipulate than
the corresponding entity it is modelling. So, a model might be an object, for
example a picture, or something as elaborate as a system.
People working in social simulation are interested in
computational models of the internal representation or models a subject has of
its environment in order to reason, make decisions, act, and adapt. Here,
models are basically a representation of the subject’s perceiving phenomena,
taking decisions, and then acting. Even more, a model might be a representation
of good action. A subject with an internal model might have several models of
certain aspects of its environment, and will take actions in accordance with a
chosen model. It in of interest in this thesis also to consider a subject’s
internal model, which may be conceived as a population of sub-models of its
surroundings evolving along with perceived phenomena (experience) and
reasoning.
So far, a world view where a subject is a
particular kind of object has been developed. It is an object that perceives
and reasons about its environment. It does this to achieve its goals. It is
also a system where ‘evolutionary processes’ are going on. These processes may
involve a population of developing models of its environment. A subject’s
internal model is useful for abstracting and modelling processes going on in
its environment.
On the other hand, the environment is also considered as a
particular kind of object. It is and evolving object; e.g., it is an object
with behaviour where not only quantitative but also qualitative changes take
place.
Finally, an agent is conceived of as a system with special
properties. An agent can be seen either as a subject or as a sub-system part of
the environment. This is in line with MAS-based Simulation, where the model of
the whole system comes up as the interaction of agents. Each of these agents is a component of the
model (system), but each agent also has an internal model of its environment,
and consequently, it can be conceived of as a subject.
In this section
Zeigler’s formalism will be recapitulated, though the examples and related
discussion are not from him. The idea is to provide in this introductory
chapter a formal description of a system as seen in simulation. Zeigler’s seems
to be one of the first and more successful descriptions of a system in
simulation. A description of both a system’s structure and a system’s dynamics
will be given. Originally, its basic formalism is intended to describe
simulation models whose structure is fixed, which are common in simulations of
systems in industry, e.g., queue systems. However, its ideas can be extended
easily to MAS. In fact, each agent in a MAS can be described as a system in
Zeigler’s formalism and the entire MAS as a composite of a hierarchy of basic
and composite agents.
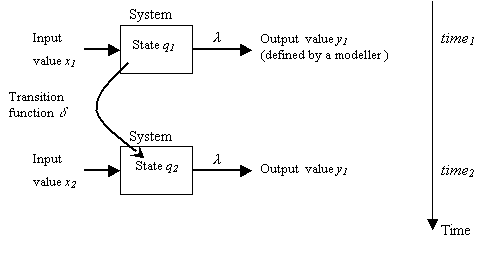
The main parts in his formalism are represented in Figure 2.1. There an input value x, and output value y,
an internal state q at two time steps, and the transition from the
former time1 to time2, are identified. The
output is a function defined by an observer, e.g., something that the observer
is interested in. The output function’s domain is an internal state of the
system. It is supposed there is a function l generating the output x
from the state of the system q. In addition, there is a change in the
system over time (e.g., there is a process): the system’s state and the input
change over time. Time is introduced as the independent variable.
More formally, Zeigler’s (1976) notation for a system S is: S =
< T, X, W, Q, Y, d, l >. Where:
T: Time
base (T = Reals or T = Integers).
X: Input value set (each input is a
sequence of values)
W:
Input segment set, subset of (X, T), W = {w / w: < 0, t > ® X, t Î T}.
Q: State
set.
d:
State transition function. d: Q x W ® Q.
l: Output function, l: Q ® Y.
Y: Output
value set. (there should exist a
set of output segments{r / r: < 0, t > ® Y, t Î T})
|
|
|
Figure 2.1. Basic
notions in Zeigler’s formalism: input values x1, x2; system
states q1, q2; output volues y1, y2; output function l; and transition
function d, changing initial state q1 into a new state q2
|
Example 2.1. Let us consider a linear system
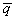 : a real vector of size n,
: a real vector of size n,
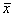 : a real vector of size l,
: a real vector of size l,
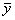 : a real vector of
size k,
: a real vector of
size k,
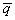 : (state) at time t2 would be given by the
application of d
at time t1 (t2 > t1)
: (state) at time t2 would be given by the
application of d
at time t1 (t2 > t1)
The set of
instances for vectors x and y gives a sequence of values over time:
|
|
|
Where t represents t1, t+1
represents t2, and A, B, C are real
matrices.
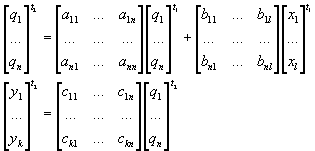
More explicitly (see also Figure 2.2):
|
|
|
Where: n = number of states qi;
l = number of inputs xj;
k = number of observation
variables or outputs yp
The set <T, X, W, Q, Y, d, l>
is called the system structure. The
subset <X, W, Q, Y> gives the static structure and the rest of the specification, d
and l,
the dynamic structure. The dynamic
structure gives the laws of change of
states. Notice that there are no laws of change either for the static or
for the dynamic structure, that is, this formalism does not consider systems
with variable structure.
Experimental Frame: Zeigler calls the experimental
frame ‘the limited set of circumstances under which the real system is to be
observed or experimented with’ (Zeigler, 1976, p. 30). He associates an
experimental frame with a subset of the input-output behaviour. More precisely,
he formalises an experimental frame E as the subset < W, Y, l, V>E,
where the first three components are as given above and V is a subset of
Y determining the range of validity of the experimental frame. This subset
of Y (i.e., V) contains the control variables of the experiment.
The remaining variables in Y are those of interest in the
experimentation (Zeigler, 1976, p. 298). Constraints are placed in
accordance with the modeller’s particular interest. In the example, a frame
would be given by <W, 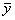 , l,
, l, 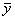 >, where Y=
>, where Y=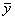 and l are given as in the example, W is (
and l are given as in the example, W is (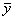 , T), where T is defined as the positive
integers (e.g., 1, 2, …) and V=
, T), where T is defined as the positive
integers (e.g., 1, 2, …) and V=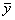 , e.g., there are not
constraints.
, e.g., there are not
constraints.
|
|
Figure 2.2. Graphic representation of a morphism for example
2.1
|
The idea is to have a hierarchy of
systems’ descriptions by increasing levels of elaboration in the sense that the
higher the level, the more detail there will be in the specification of the
system (e.g., more aspects of his structure will be known). This would be
valuable for comparing models’ descriptions and to know the degree of
specification a model has.
At a first level (level 0), a collection of
inputs and outputs is known over time, but there is no idea about the
relationship among them. In a second level, an input-output relation is
known. Different outputs have been associated with the same input, and, vice versa, different outputs have been
related to the same input. A third level of specification will be
useful for associating an input with an output, that is, there is a function
relating in a unique manner an input with an output. This level is the most
commonly used in science, e.g., in mathematics and physics. Notice that still
the notion of process is poor - the weak notion of process is in the output,
which can be specified as a function over time. At this level simulation is not
an important tool, as the output can be generated only as far as the input and
the function input-output are known. This level is not rich enough for helping
in those cases where the behaviour of the system is difficult to model via a
function, but depends subtly on internal variables (e.g., the state) of the
system (e.g., in a social system, or in a queue system). It is in these cases
where simulation becomes helpful. In the fourth level (level three in the
specification), it is supposed that a function for changing the
internal state of the system is known. The specification of change over
time of a system’s state brings in clearly the notion of process. Other aspects
of a system, such as the output, can be defined in terms of a system’s internal
state. In the higher level, e.g., at level four, a system is defined as the
composite of interacting systems at level two. This level is useful to
describe, for example, an agent in a MAS composite of more elemental
sub-agents. In fact, it can be used to describe a hierarchy of agents, e.g., a MAS.
More formally, from Zeigler (1976):
Level 0: Observation Frame, S = < T,
X, Y >. The sets of inputs and
outputs are distinguished but it is not known how they interrelate.
Level 1: Input/0utput (I/O) Relation
Observation (IORO), S = < T, X, W, Y,
R>, (R Í W 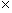 (Y,T), where (w,r) Î R ®
(implies) dom((w) = dom (r )). The
relation between the input and output sets is distinguished, but it is not
possible to differentiate among the different outputs associated with one input
and vice versa.
(Y,T), where (w,r) Î R ®
(implies) dom((w) = dom (r )). The
relation between the input and output sets is distinguished, but it is not
possible to differentiate among the different outputs associated with one input
and vice versa.
Level 2: I/O Function
Observation (IOFO), S = < T, X, W, Y, F >, (f Î F ®
(implies) f Í W 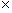 (Y,T) is a
function, and if f = (w,r) then dom (w) = dom (r )). At
this level, there is a function between input and output sets which permits one
to differentiate between the different outputs associated with an input. It is
granted by the knowledge of the initial
state. Until this level, a move from a lower level to a higher one allows
more predictability about the output, given the input, but still there is no
knowledge of the system’s states.
(Y,T) is a
function, and if f = (w,r) then dom (w) = dom (r )). At
this level, there is a function between input and output sets which permits one
to differentiate between the different outputs associated with an input. It is
granted by the knowledge of the initial
state. Until this level, a move from a lower level to a higher one allows
more predictability about the output, given the input, but still there is no
knowledge of the system’s states.
Level 3: I/O System Specification, S = <
T, X, W,
Q, Y, d,
l >. At this stage, the state set, the
transition and output functions are known, but still there is no distinction of
the system’s components.
Level 4: Coupling of
Systems. Here a system is specified as a coupling of several sub-systems or
components. Four elements are given: the name of the sub-systems, the
specification for each component at level 3, the influencers of each one (other
components), and the interface function specifying the input of each component
as a function of the outputs of its influencers and the input to the system.
In Zeigler’s formalism, it is supposed that the transition
function is invariant over time (e.g., a system’s dynamic structure is
invariant); that is, whenever it is applied over the same initial state and
input segment, the same output segment will be generated.
Also, notice that the specification at level
zero only gives a pair of the sets of inputs and outputs plus the idea that
they are changing over time. There is no specification of structure. This seems
to be one of the simplest specifications of a system that can be found in the
literature.
Heylighen also formulates specifications of very simple
(plain) systems, for example, systems for which it is not necessary to
specify their components or even their states (Heylighen, 1995). He brings in
the example of an electron. An electron is considered as a system though no
structure has been identified and only the notion of certain behaviour gives
its identity. However, ‘It has states given by positions, energy or momenta …
and their evolution can be expressed by the Schrödinger equation’ (Heylighen, 1995,
http://pespmc1.vub.ac.be/papers/MST-ConVar.pdf, p. 4). In fact, this model will
be at least at level three, as the transition function is known. Heylighen
considers that a system is an entity suffering internal change while keeping
stability in the sense that it shows differentiation with respect to the
environment as an individual unit. He expands this notion, summarising a system
as a ‘constrained variety or constraint on variety’. This idea can be used for
describing systems of order zero: ‘The total set of connections (Cartesian
product of the set of possible inputs and set of possible outputs) might be
interpreted as a maximal possible variety, the subset defining the system as a
limited variety, to which actually occurring input-output transitions are
constrained’ (idem, p. 5).
When modelling in traditional economics, the
economic system is usually represented at level 4 but the economic agents
(e.g., organisations or people) are simplified to level 2. In social simulation
this system is modelled at a higher specification level, as the relevant
aspects of an economic subject with bounded rationality, namely, its internal
(cognitive) model, are modelled at level 4. One interesting question is whether
the simplification made in traditional economics is well justified in the
dynamic economic environment of today.
MAS has been successfully applied to
the modelling of complex systems described in terms of components.
A MAS consists basically of a hierarchy of agents. Each
agent can be described as a system according to Zeigler’s formalism, as was
briefly shown in the example given in section 2.6.1. The lower level of agents in a MAS, that of agents
without sub-agents, will be described at level 3 in Zeigler’s formalism (see
paragraph 2.3.1). The other, higher levels (the containers) could be
described at level 4.
Agents change as their rulebase changes over time. A
relevant example is the evolution of their cognitive models given via a set of
rules. The change of rules over time allows more creative and subtle processes
than those happening when only elimination and introduction of agents are
implemented.
In declarative programming, laws of behaviour are given as a
set of rules, which are ‘atomic’ components admitting to be modified,
eliminated, created, and replaced. This is appropriate for evolving the dynamic
structure of agents.
Now a criterion for comparing models
will be reviewed. This comparison is based on the concept of experimental
frame: ‘equivalence’ among models is always relative to an experimental
frame. This conception of equivalence is based on the mathematical concept of
morphism. A weaker notion of model equivalence will be presented in section
2.6.1. This will be useful for simplification, validation, and alignment of
models.
Evaluating morphism consists in checking if the same
output-input set a modeller is interested in (e.g., the experimental frame) is
observed in two models. It might consist also in checking if a subset of the
output a model offers under certain conditions (this gives an experimental
frame) coincides with the correspondent outputs other models generate under the
same conditions; in such a case it is said that there is a morphism between these
two models. As a system’s output depends on the system’s state, also
‘equivalence’ between the compared system’s states has to be checked. In fact,
a system S will be called ‘equivalent’ to a second system S’
(that is, a morphism exists from the second to the first system) if the state
and output of system S can be accessed via a mathematical transformation
(the morphism function) from the state and output, respectively, of system S’
at any time and under certain conditions of experimentation (e.g., under an
experimental frame).
Notions discussed in this section can be used to classify
and assess homorphisms appropriately when using the methodology to be developed
in Chapter 5 for comparing models. Notions of homomorphism associated with this
methodology will be discussed in section 5.10.
Consider now the notion of morphism as given by Zeigler.
There is a morphism between S = < T, X, W, Q,
Y, d,
l > and S’ = < T’, X’, W’,
Q’, Y’, d’,
l’ >) if there exist functions g, h,
k such that (Zeigler, 1976):
Each evaluation of d takes the state q and the input x at time t and generates
the new state q for the next time
step t+1. The output function l
takes the state at time t to generate
the output, also, at time t. This is
represented in Figure 2.3.
|
|
Figure 2.3. Graphic representation of a homomorphism
|
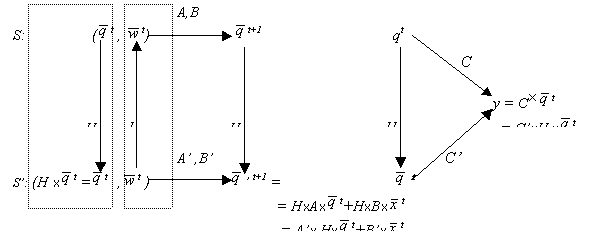
If S and S’ have the same observation frame,
that is: T = T’, X = X’, Y= Y’, W = W’,
and 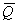 is equal to Q, then g and k are the
identity functions. The graph in Figure
2.2 becomes as shown in Figure
2.4, and equations 4 and 5 turn out to be:
is equal to Q, then g and k are the
identity functions. The graph in Figure
2.2 becomes as shown in Figure
2.4, and equations 4 and 5 turn out to be:
S’ is an image morphism of S, and the function h is called a homomorphism. If in addition h is
one to one, it is said that there is an
isomorphism between S and S’ (or that S and S’
are isomorphic).
|
|
Figure 2.4. Morphism between systems S and S’
under a similar observation frame
|
|
Zeigler (1984, p. 251): explains a valid simplification in
these terms: ‘We say that a lumped model [for us, S’] is a valid simplification of a base model
[for us, S] in frame E [for us, an observation function l]
if the two models are equivalent in E [e.g., a morphism from S
to S’ exists] and the lumped model is simpler than the base model with
respect to some measure of complexity.’
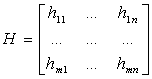
Example 2.3
Continuing with the example of the
linear system, we define H as:
|
|
|
|
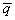 ’ is the state of the system S’ given as a
vector of size m. It is supposed that the number of states in S’
is smaller than the number of states in S (that is m < n). ’ is the state of the system S’ given as a
vector of size m. It is supposed that the number of states in S’
is smaller than the number of states in S (that is m < n).
So, at any t:
|
|
|
|
Or, more explicitly:
|
|
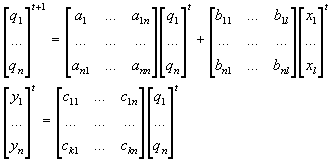
|
|
And for S’:
|
|
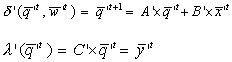
|
|
The two systems have the same number of outputs and
inputs. However, system S’ has a smaller number of states.
Now, we can look for conditions to satisfy transition and
output function preservation (4a. and 5a.; see also Figure 2.5)(here it is assumed time variables 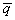 , , 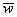 , and , and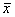 are evaluated at time t): are evaluated at time t):
|
|
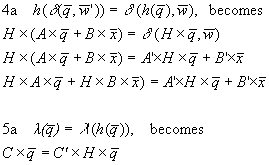
|
|
As is known from previous equations:
|
|
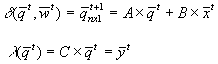
|
|
Vectors 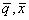 , and , and 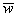 are evaluated at
time t. are evaluated at
time t.
For any t and
arbitrary vectors x and q, 4a, and 5a, are true
if:
|
|
|
|
Example 2.1. A
case where n = 3, m = 2, k = 3, and l = 2 is:
|
|
Example 2.2.
Again a case where n = 3, m = 2, k = 3, and l = 2:
|
|
|
It is easy to verify conditions 4 and 5.
Systems S and S’ have a similar number of inputs and outputs. The
size of the space of states is different, three for S and two for S’.
We notice the exhaustive partition that function H makes in the space of states
of S. The first component of 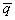 ’ depends on the first component of
’ depends on the first component of 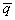 , and the second component of
, and the second component of 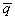 ’ depends on the remaining two and three components of
’ depends on the remaining two and three components of 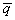 . As the relation among states is not one to one, this is not
an isomorphism (see Figure
2.5).
. As the relation among states is not one to one, this is not
an isomorphism (see Figure
2.5).
Assume a simplified system for S: S’ = < T’,
X’, W’,
Q’, Y’, d’,
l’ >, is given. S’ would be
smaller in the sense that Q’ could be inferred from Q, but the
opposite would not necessarily follow.
Zeigler identifies at least 4 ways to simplify a model:
1.
Dropping of components, descriptive variables, or relations.
2.
Replacing one or more deterministically controlled variables
by random ones.
3.
Coarsening the range set of one or more descriptive variables.
4.
Grouping components into blocks and aggregating the descriptive
variables also into blocks.
If S’ is a homomorphic image of S,
the behaviour of (S’)’ is a subset of the behaviour of (S)’.
In fact, it is possible to generate any state and any output of S’ from S,
using the homomorphism function h. Should S’ be a valid
simplification in a given experimental frame, either of the models generates
the behaviour of interest, but it would be cheaper in computational terms to
simulate system S’. Moreover, in this experimental frame, the behaviour
of (S’)’ is the behaviour of (S)’ constrained. In declarative
programming, where functions are given in terms of rules, S’ might be
seen as S plus some constraining ‘metarules’ (as behaviour of S’
is accessible form S). This notion of metarules is used by Holland
(1998). In the example, those metarules will constrain the space of states of S,
eliminating some sort of redundancy.
In such an example a redundancy occurs when given both
values q2 and q3 because only one value,
the total q2 + q3, is sufficient for calculating the required output, as the
simplified system S’ shows. The metarule that would have to be added to S
in order to get S’ will imply this condition. Note that columns two and
three of C’ are identical. Such a condition would be expressed
mathematically as:
The resulting output and the transition from two states differing only in the
two components (q2, q3) will be similar
(under the experimental frame defined above) if the sum of q2
and q3 gives the same result.
In this particular example S’ is simpler than S,
as the systems are of a similar nature (linear systems) but less memory is
necessary to keep information about the states of S’ and less
calculations are necessary to generate a simulation state transition - the size
of the matrices and vectors involved are smaller than those in S. If S’
and S had different natures, such a comparison might not be so
straightforward. Here the measure of complexity is defined in terms of
computational resources, namely in terms of the amount of memory necessary to
keep a system’s state and the number of manipulations required for a simulation
step transition.
Given an experimental frame (e.g., the sort of input-output
behaviour of interest) and a transition function, the homomorphism might be
defined in several ways corresponding to alternative manners of simplifying.
However, given a system and an experimental frame, it might not be easy or even
possible to find the ideal simplest system, S’, of S under such a
experimental frame (assuming it exists). A notion of satisfying seems to be
convenient. In addition to the experimental frame and modeller’s goal,
available theories, methodologies, and modelling tools (e.g., for simulation)
seem to be other factors involved in simplifying.
This formal definition of system homomorphism has been
useful in simulation. However, generally in practice this formal (mathematical)
notion of homomorphism cannot be applied, as no homomorphism as seen in
Zeigler’s formalism exists and alternative weaker notions of homomorphism have
to be used for comparing systems. This point will be addressed in more detail
in section 2.6, where an illustrative example will be given.
Call S(t) and S’(t)
the structures of systems S and S’ respectively at time t.
Extrapolating our notion of morphism for a system with static structure, S’
is a simplification of S if S’(t) is an image of S(t) under
a suitable morphism. However, to require morphism equivalence at any
time instant seems to be too strong, and even unrealistic in practical
applications. A weaker notion of ‘similar’ evolution among structures might be
more convenient where evolution of the structures at different time instants is
allowed. To account for this, more relaxed conditions for a valid
simplification when the systems are under structural evolution would have to be
looked for.
The homomorphism function might change over time, e.g., h
= h(t). If the function h(t) is given in terms of rules, its change
over time can be implemented by modifying only some rules rather than by
redefining the whole function h(t), as would be done in a procedural
program. This gives a sort of modularity and flexibility. Consequently, to
follow the structural evolution of two systems and express homomorphism between
them seems to be easier in a declarative program than in a procedural one.
MAS built in languages like SDML are an example. Structural
change such as elimination and/or introduction of components of the system
specified at level 4 (as seen above) or modification of components’
interrelations can be made in modularly. In addition, processes, e.g., dynamic
laws of systems, can be modified by changing, aggregating, and/or eliminating
rules. Also rules can be shared among agents and processes. This gives a sort
of modularity at the level of process implementation useful for considering
changes in the dynamical properties of a system. Rules could be seen as an
object that might be created, shared, inherited, aggregated, and destroyed.
Rules can also be grouped conveniently and reused in different modelling
specifications (e.g., a module hierarchy in SDML).
This sort of structural change, though far beyond what is
allowed by known simulation languages in industry (e.g., SLAM II, Pritsker,
1995), is still very limited compared with structural change in empirical
systems. In empirical systems structural change occurs at ‘infinite’ levels.
Even more, in highly evolved systems (or systems at a high level of complexity;
see Chapter 4), this process might be creative (Domingo et al., 1996a).
Validation
is a particular case of weak homomorphism between two systems. A sort of
equivalence under a weaker criterion than the mathematical morphism defined
above is applied to check agreement between two systems. A weak notion of
homomorphism will be described in sub-section 2.6.1. It is supposed there is a
bigger system S, e.g., reality, and the model or system to be validated S’.
S’ will be a valid model if it is a homomorphic image of S under the chosen
weak homomorphism criterion.
Aggregation of models consists in integrating several models
representing complementary aspects of a system rather than each component. Simulating
each of these components usually requires a lot of computational resources, and
so it is convenient to find a way to simplify them. Again, the idea of a weak
homomorphism is applied, first to simplify the components, and then to validate
the new, ‘bigger’ model resulting from that aggregation. Some researchers in
social simulation have proposed creating a cascade of integrated models (Moss et al., 1998b). They describe it as a
‘bottom up’ modelling procedure in contrast to the ‘top down’ modelling procedure
used in classical models of economics and climate change. They also argue that
validation might be done against collected data in reality or ‘domain experts’.
Finally, two models are aligned if there
is a weak homomorphism among them, the idea being to compare models in
different platforms, although one model is not necessarily simpler than the
other. This notion is used in Axtel et
al. (1996) for comparing two programs built independently for modelling a
similar case. The criterion used in this work for checking homomorphism is
weaker than the one given by Zeigler and discussed above (this criterion will
be discussed in sub-section 2.6.2).
Several factors are involved in the
difficulties associated with proving homomorphism, among them are: lack of
precision in measuring the phenomena, error propagation in the computer, and
factors little understood in the empirical system an commonly modelled as
random processes. Usually, it is not possible to cancel these restrictions, and
the criterion of perfect agreement in a relation of homomorphism has to be
replaced for one of approximation in practical applications.
In this section the relaxation of the validation procedure
for the case of simulations of models with fixed structure will be reviewed
(Zeigler, 1976).
‘The validation criterion becomes one of ‘REASONABLE’ agreement between the
systems’ outputs The notion of reasonable agreement is formalised in a concept
of tolerance. Basically, it is defined as a metric (|| . ||), over the difference between the outputs
(behaviour of interest) of the two systems, S and S’. This
difference is required to be smaller than a predefined tolerance. One of the
most popular metrics is the square mean.
To calculate this measure of agreement exactly, it is
usually necessary to sum over all outputs of interest. Consequently, this
requires a post hoc analysis of all
trajectories. However, it is not usually possible to generate all the outputs
of a system via examination of the simulation trajectories. Alternative looser
simplification procedures are needed. Techniques where only a limited number of
trajectories are analysed are associated with post hoc inspection of
trajectories where weak notions of morphism are applied. Among the
existing techniques for doing this looser post hoc analysis are scenario
analysis and Monte Carlo techniques. Given certain drawbacks of these existing
techniques, additional methods are an open area of research (see section 2.10). It is the main aim of this thesis to propose
alternative methods, but yet practical, for analysing simulation dynamics,
which rest in stronger notions of morphism than the weak ones to be described
in this section (see Chapters 5 to 7).
Different weak homomorphism criteria can be defined.
Taking a phrase from Zeigler (1976, 330) (he uses f for || . ||):
‘f picks out those aspects of the output
CONSIDERED TO BE IMPORTANT FOR DETERMINING ACCEPTABLE AGREEMENT’. As
pointed out before, in Zeigler’s simulation theory only quantitative change in
the system’s outputs is taken into account, this is also true when checking a
weak homomorphism.
Example 2.4. A simplification using a
weaker homomorphism criterion
Suppose there are two MAS-based models of a
trader-distributor interaction. There will be two principal types of agents:
Trader and Distributor. Each model is defined as the interaction of several
traders and distributors. A distributor’s main task is: to place orders to a
trader. A trader’s main tasks are price- and sales-setting, and
price-imitating. The experimental frame will be to observe changes in prices,
sales, and orders over time.
Assume now that in a first model the agent trader contains
sub-agents warehouses and trucks, where trucks are used for delivering goods to
distributors and warehouses are employed to keep control of the input-output of
goods.
Now suppose that in the second model warehouses and trucks
do not exist as agents. Data and rules kept in warehouses in the first model
are now kept in the trader’s database and the rulebase respectively (e.g., now
the level of goods can be represented as: goodLevel(Warehouse, Amount)).
Trucks are just obviated and delivering is modelled using a delay function.
The first model of trader needs to be specified at level
four (as it has components), while the second model can be specified at level
three (see the next diagram for an overview of the first model of a trader).

Other facts about this first model are:
The input of a sub-agent (truck or warehouse) depends
on the output of some of the other sub-agents (the influencers). In this
example, the interaction between a warehouse and trucks serving it is simple: a
truck takes produce from a warehouse in accordance with the level of this
product, and a warehouse updates its level of product in accordance with the
amount taken by the trucks. The states of warehouses and trucks are considered
accessible by their container (trader).

Now, let us see how a trader is modelled in the simplified model
trader-distributor:
A simplification between these two models
cannot be based on a homomorphism as it was originally defined, but only on a
weaker criterion. Proofs of strict homomorphism might be more difficult than
the simulation itself and quite unlikely to be achieved successfully. As
previously stated, no strict homomorphism exists in practice. Let us assume
that Monte Carlo techniques are chosen as the weak method for comparing the two
models.
Our experimental frame (see above) specifies interest in
observing the behaviour of prices, sales, and orders. Consequently, the
evaluation criterion has to be based on these outputs.
The comparison may be made following these steps:
1.
A random set of simulation trajectories for each model is
generated. It can be implemented using different random seeds for calculating
random variables for different trajectories. Random variables are used for
modelling certain little-known aspects in the simulation model. For example,
assume that for price-setting a trader imitates other traders’ prices. Then, a
random variable can be introduced for modelling a trader’s choice of another
trader.
2.
Data of interest are collected from the generated
trajectories. In this case data about sales, orders, and prices are gathered.
3.
Then a statistical test (here the weak criterion for comparing
the two models) is applied to check the hypothesis that the two samples (e.g.,
each pair of samples of orders, sales, and prices) are coming from a similar
statistical distribution and so are statistically similar. Among the methods
for making this comparison is the non-parametric Rank Sum Test (Hoel, 1966).
Should the test prove successfully, it would be said that the models are
equivalent in accordance with this weak notion of homomorphism. As the second
model is simpler than the first one (notice that it has less components and
less variables), there would also be a valid simplification.
Notice the weakness of this procedure in that the
conclusions valid for the explored subset of trajectories are extrapolated by
using probabilities to the whole space of trajectories, even though unexpected
things can happen at the randomly left trajectories. As previously stated, it
is the purpose of this thesis to propose alternative ways for doing the searching
for trajectories, and then, based on this, to define alternative notions of
morphism.
In simulations where the structure
of the model undergoes qualitative change, the experimental frame is generally
defined not only in terms of quantitative outputs but also in terms of the
structural change of the system; that is, qualitative changes are an aspect of
interest. For example, in a MAS-based simulation where agents are eliminated
and introduced, the behaviour of interest might be the number of agents of a
certain type appearing at the end of a simulation. Notice that in this case
quantitative measures can be defined over the qualitative change.
So, a way for doing the qualitative comparison is by
defining quantitative measures over qualitative behaviour. Illustrations
already exist in the literature, for instance, that given by Axtell et al. (1996) for the alignment of
models. They compare the average number of stable regions observed in the
simulation of a model of cultural transmission. In this experiment, the factors
are the number of cultural attributes, the attribute’s levels, and the size of
the territory where the interaction happens. The statistical comparison is made
only at one time instant of the simulation (at the end of it). Axtell et al. also mention an alternative
procedure using statistics: to observe if certain internal relationships among
variables hold in both models. They call this comparison ‘relational’
equivalence, and the statistical one ‘distributional’ equivalence.
In a simulation processes of three types can be
identified, (1) those programmed or explicit in the simulation design (which
can be used for verification); (2) those not clearly given in the design but
desirable in the model as well as being well known in the modelled system
(which can be used for validation); and (3) those called open aspects, which
are little understood in the target system and about which a simulation might
give hints and help a modeller hypothesise about the behaviour of the model
and, extrapolating, about the behaviour of the target system.
For example, in an event-driven simulation of a queue
system, the process of arrival of entities into the queue might have been
programmed to follow a probabilistic distribution. This first sort of behaviour
can be foreseen and so is not of interest for validation. This is an aspect to
be verified. Verification can be achieved by comparing the design of the model
with some formal specification. In fact, verifying a model consists in
comparing the structure of the model with some specification given by a theory.
On the other hand,
in the event-driven simulation a modeller might notice certain behaviour about
the size of the queues not directly given in the simulation design. Checking if
the corresponding behaviour in the target system - which may supposedly be
measured in some way (e.g., via a statistical sample of the behaviour of
interest) - coincides with behaviour in the simulation is what is called
validation of the model.
Finally, there should exist many other features a subject (a
modeller) does not comprehend well in the dynamics of the modelled system and
which he wishes to understand better by observing the simulation. For example,
some special features called emergent tendencies are worthy of special
attention in social simulations.
Strategies
in event-driven simulations are based on the use of a future event list (FEL).
Each event is associated with: the time when it will be activated (activation
time), possibly additional conditions for the event to be activated once the
time-condition is satisfied, and the consequences of the event (namely changes
to be made in the system’s state and the scheduling of further events). Events
in the list are ordered by their activation time. For example, in a queue
system, the event ‘arrival of an entity into the system’ will be associated
with the arrival time (activation time of this event), other conditions for
such an arrival to happen, changes to be implemented in the state of the system
(for example, to place the entity in the queue if the queue is smaller than a
certain size), and, finally, the scheduling in the FEL of a new arrival.
As can be seen from
these examples, the FEL is used for guiding the state transitions over time.
Size of time steps is taken as the difference between the time of activation of
each pair of consecutive events in the FEL. Two of the most popular strategies
in event-driven simulation are simulation by events and simulation by
processes. In event-driven simulation each event is programmed in a separate
module and a main program executes that module corresponding to the next event
in the FEL. In simulation by processes, the process an entity carries out is
the key aspect. The program consists in a sort of net for the ‘life-cycle’ of
the entity. For example, in a queue system, the entities are those units
queuing and their cycle of life is given by a succession of events: to arrive,
to queue, to be served, to leave. The program consists of a net of nodes
following the temporal order given by the entity’s life-cycle, where the
consequences of each event (as well as possible decisions the entity has to
take or decisions of the system, e.g., gates) are programmed. An event fires as
the entity reaches the associated node(s). So nodes are used to represent:
entrance to the system, queue, service, output of the queue, and exit
(destruction of the entities). Examples of languages where these strategies have
been implemented are SIMAN, SLAM, GLIDER, and SPSS. This sort of simulation is
common in industry.
The basic aspects of a system with
variable structure and its simulation will be reviewed in conformity with the
ideas of Domingo et al. (1996, 2000);
Testa et al. (1999), and Heylighen
(Heylighen, 1989, 1991, and 1995). Then speculation about simulating structural
change according to Domingo’s ideas and a MAS will be presented.
Testa et al.
consider it fundamental to recognise change at both levels: at the level of the
static structure (what he calls form) and at the level of the dynamic structure
(function). They call this change ‘fluctuation’. More precisely, they talk
about ‘fluctuation within a probabilistic range’. They argue that there is a
mutual dependence among the two changes and note that such an interdependence
cannot be ordered either hierarchically or causally. They describe the
processes of dissolvence and emergence as the two facets of the same coin where
a whole (system) arises from its components (sub-systems). The first is the
rise of new properties of the whole and the second the constraint of its
components ‘in a synergic process of integration and re-organisation’. Examples
of biological systems are given.
In Domingo et al.
(2000), another concise idea of structural change is found, for here they
affirm that ‘in structural change systems change the behaviour, the components
and the relations among them.’ They identify other processes leading structural
change in addition to that of aggregation described by Testa et al. Among them are bottom-up and
top-down changes. In the former case the process of structural change is driven
from above - the whole system drives the constraint in, e.g., properties of the
components and elimination or introduction of new components. In the latter
case, the parts are responsible for directing that process. Moreover, they
argue that the two processes can be present simultaneously. For example, a
revolution can be a bottom-up change led by members (components or actors) of a
state (e.g., groups, associations, people) creating changes in the whole system
(the state). The opposite happens when there are economic associations among
countries. Then the new rules for the economic interchange among the involved
countries are elaborated at the top level and then ‘imposed’ upon the lower
levels of the system (the economic actors). However, the systems these examples
refer to can present both kinds of changes over a time period of enough length.
For example, in the case of a revolution, after the new political force takes
power, it starts promoting changes from above (top-down) as it implements, for
instance, its economic and educational policies.
Domingo identifies two main problems for the simulation of
structural change (SC):
·
First, those related to the laws of change, that is,
aspects related concerning when to change the structure and how the variation
selection of structures will be given.
·
Second, that of the level of aggregation. In nature,
the aggregation of sub-systems seems to happen at many levels (perhaps at
infinite levels) starting from small atomic levels possibly still unknown in
physics. Obviously, its modelling in a computer cannot be attempted. In this device
only certain levels of aggregation of structural change can be modelled (the
relevant ones for certain purposes and in accordance with the available
modelling tools).
A graphical representation of several levels of control,
where structural change is allowed, is given in Figure 2.6.
|
|
Figure 2.6. Graphical representation of several control levels
where structural change takes place
|
Example 2.5. MAS-based
Simulation: A Weak Case of Simulation of structural change.
In MAS some levels of aggregation
are at the level of agents. Agents can be created, destroyed, and their
rulebase modified. There are several levels of aggregation but the number of levels
is finite. Moreover, these structures
(agents) and levels of aggregation are fixed. Another level of
aggregation is that of the cognitive model of the agent. Examples of agents’
internal models are presented in Moss et
al. (1998a). Here aggregation occurs
at the level of rules. In the following pages we will present examples of how
the problems averted to by Domingo have been handled in MAS.
At the level of aggregation of agents, since structures are
fixed, the first problem, (namely the process of variation selection) is solved
in an easy way – it is simply obviated. At the level of cognitive models more
elaborate procedures have been used: evolutionary programming. Here rules are
evolved using genetic algorithms or genetic programming (Edmonds, 1998). These
two examples of simulation of SC are part of two strategies Domingo et al. propose to solve the named
problems. Structural change in the case of an agent can be a decision either of
the environment or of the agent itself. For instance, a trader in a market
might be eliminated by the economic environment (e.g., if his profits are too
low) or he may choose to leave the market. A cognitive model can suffer
structural change when the agent undergoes a new experience.
Both Heylighen and Domingo recognise the importance of a
meta-model when modelling structural change. The meta-model, or controller,
would be responsible for solving the problems Domingo has indicated: namely, to
decide when the change happens, to implement the process of variation selection
of structures, and to choose the aggregation level (see also Heylighen, 1991b;
Domingo et al., 1996a). Several aspects of their proposal coincide with the
strategy followed in a technique to be presented in Chapter 5 and implemented
in the example contained in Chapter 7.
A post hoc
analysis of a simulation consists in examining outputs obtained from the
simulation (as has already been described in this chapter). This is the
strategy used in many simulation studies to understand a simulation after it
has occurred owing to difficulties in studying it from its design. Conclusions
of this analysis can be extrapolated to the modelled ‘real system’ (if it
exists) under certain conditions (e.g., the morphism criterion discussed in
previous sections). In this thesis a post
hoc analysis is of special interest for assisting in explaining emergent
tendencies in a simulation.
Usually it is not possible to include all possible simulation
trajectories in a post hoc analysis of a model-based simulation, as
might be suggested by a strong notion of morphism like that of Zeigler
introduced in section 2.3.3. An exhaustive generation of simulation trajectories
in a simulation is generally impracticable owing to the limited computational
resources available to a modeller. It might also produce too much information
and make the analysis of the outputs difficult. Because of this, alternative
approaches have been developed along the weak idea of morphism offered by the
notion of approximation introduced in section 2.6. Among these alternative methods are scenario
analysis and Monte Carlo techniques.
Scenario analysis consists in analysing a modeller’s
selected subset of trajectories. On the other hand a Monte Carlo Analysis
consists in analysing a randomly chosen subset of trajectories. In a Monte
Carlo study, conclusions from a ‘big enough’ sample of trajectories are
probabilistically extrapolated to unexplored trajectories (see section 2.6.1).
Both of these methods leave unexplored trajectories. Neither
of these explorations is exhaustive. In the first method the omitted
trajectories depend on the ‘subjective criteria’ a modeller applies to choose
the trajectories to be explored and, in the second one, they are left randomly.
Because of this the analysis is limited, as the conclusions cannot be
generalised and applied in wider theory – only probabilistic generalisations
are allowed (in the second method).
On the other hand, probabilistic extrapolation is valid only
if small changes in the settings of the simulation produce small changes in the
outputs of the simulation – e.g., if outputs are continuous with the settings
of the model. As this assumption is not valid in complex systems (e.g., in
systems with chaotic behaviour), a Monte Carlo analysis of a simulation of a
complex system might omit trajectories likely to happen in the ‘real system’
where the behaviour of interest might be quite different to that observed in
the explored ones. This arbitrariness in the chosen trajectories engenders
difficulties for generalising conclusions when simulating complex systems.
The dynamics of complex systems are usually very sensitive
to changes in the properties of the components and, in general, to the
evolution of the structure of the system itself, since small changes in the
properties of the system might result in big changes in the outcomes of the
system. For example, the behaviour of a chaotic system is very sensitive to
changes in the initial conditions of the simulation; a slight change in the
initial conditions may produce big alterations in the processes this system is
undergoing (e.g., that system (in weather forecasting) defined as the
surrounding of a geographical area determining the weather conditions of this
area). Another example is a social system. In a social system chaotic behaviour
is present because of its high level of complexity. It is sourced mainly in the
high number of entities (humans) interacting in a society and in the complexity
of each of these entities (see the discussion concerning modelling systems at
high levels of complexity in Chapter 4, especially section 4.3.3).
Similar susceptibility is expected to be present in the
dynamics of a simulation of a complex system. For example, phenomena in a
MAS-based simulation of a social system might be unexpectedly contingent on
changes in the parameters of the model and the choices of the agents, so that
small changes in parameter-settings or in agents’ decisions might result in
significant changes in the simulation outputs. This inappropriateness of
modelling complex systems by using classical modelling approaches based, e.g.,
on averages, has already been discussed by many thinkers. One of them,
Crutchfield (see, e.g., Crutchfield, 1992), argues that in these systems,
‘fluctuations dominate behaviour and averages need not be centred in around the
most likely value of its behaviour. This occurs for high complexity processes …
since they have the requisite internal computational capacity to cause the
convergence of observable statistics to deviate from the Law of Large Numbers’
(Crutchfield, 1992, p. 35, in the version of the paper available at http://www.santafe.edu/projects/CompMech/papers/SATTitlePage.html).
In this statement, Crutchfield seems to be considering systems at a high level
of complexity, e.g., those with a vicarious mechanism (whose ability and
activity he refers to as ‘internal computational capacity’), such as human
systems. Aspects of these systems and their simulation are examined in section 4.3.3.
All this creates doubts about the appropriateness of
techniques that arbitrarily leave simulation trajectories unexplored as well as
about the use of statistical summaries for studying simulation outputs. This
thesis is aimed at developing alternatives to such existing methods, for
studying complex systems: on the one hand, stronger notions than that of
approximation for overcoming drawbacks in existing techniques but more
practical than Zeigler’s original notion of morphism (for this,
‘constraint-based exploration of simulation trajectories’ and a ‘platform of
simulation architectures’ will be suggested), and, on the other hand,
alternatives to the use of ‘statistical summaries’ for analysing simulation
outputs are needed (in this sense, the ‘envelope of simulation trajectories’
will be proposed).
Ideas not commonly used in
simulation such as those implemented in theorem-proving and Automatic Reasoning
(described in Chapter 3) will be introduced for exploring the dynamics of a
system. A proof of a theorem in a simulation rests in a more exhaustive
exploration of the dynamics of a simulation than that carried out in the
traditional methods named above (see Chapter 5 and, in particular, section 5.5). A proof will allow a modeller, on the one hand, to
explore a fragment of a simulation theory, and, on the other hand, it will
permit the implementation of measures of behaviour other than averages in the
explored simulation theory. As we are interested in studying emergent
tendencies, we propose, as an alternative measure of behaviour, the envelope of
the tendency in the explored fragment of the simulation theory. Hence, the
methodology to be proposed should be a valid alternative to existing methods
for analysing the simulation of a complex system.
In addition, this methodology will be in line with
Heylighen’s call for computational mechanisms for helping a social agent (in
this case a modeller) to cope with the complexity of the social system it
inhabits (see section 4.3.4).
One of the main purposes of this thesis is
to develop a methodology to analyse and understand the dynamics of simulation
in MAS. It is of interest to analyse regularities in the dynamics of a
simulation not explicitly given in the simulation design and which are relevant
for understanding the modelled system, despite being poorly comprehended by the
modeller (these regularities will be called ‘emergent’). As observed in section
2.10, existing methods for analysing the dynamics of
simulations of complex systems have serious drawbacks and this thesis aims at
looking for alternative approaches.
As
was shown in the previous chapter, those existing methods for investigating
simulation behaviour allow one to draw only limited conclusions about the
dynamics of the simulation in only very specific spaces of the simulation
theory. Those methods explore only a single simulation trajectory at a time and
use the notion of approximation for proving morphisms. It is the intention in
this thesis to investigate about more powerful methods for analysing such
dynamics, that will permit one to reach more general conclusions and to define
stronger notions of morphism than those allowed when using the notion of approximation.
Concretely, this thesis aims at developing methods for proving theorems about
the dynamics of a simulation. As it is usually difficult to explore the whole
dynamics of a simulation (e.g., about the whole simulation theory), this thesis
seeks to find methods to prove theorems with respect to a sub-space of the
space of the simulation dynamics and, correspondingly with respect to a
fragment of the simulation theory.
Though in this thesis a methodology for
proving theorems in a simulation will be developed, this work is also
exploratory in the application of theorem-proving strategies for proving
tendencies in the dynamics of a simulation. There have been no previous
developments in this line, as far as is know. Because of this, a review of a wide
variety of existing methods, not only those directly related to the strategy to
be proposed in this thesis, will be considered in this chapter. This review
might be used for classifying: the theorem-proving strategy followed in the
theorem-prover to be used to implement an example (e.g., OTTER), existing
methods for simulation, and the theorem-proving strategy for proving theorems
about the dynamics of a MAS to be presented in the next two chapters.
The introduction to simulation given in the
previous chapter, together with the review of formal aspects of
logic-programming and theorem-proving to be presented in this chapter, will
provide the theoretical background for a move towards the methodological
developments to be given in the next chapters of this thesis. The main
intention of this chapter is to provide a review of the different strategies
for theorem-proving.
First, in section 3.2, basic conceptual
aspects of proving theorems, using computational algorithms, will be shortly
addressed. Then, the difficulties that have been found for finding a good and
general computational algorithm to prove satisfiability/unsatisfiability of a
formula will be briefly touched upon. Also, in this section, a basic conceptual
framework related to proving theorems in a theory useful for the rest of the
presentation will be offered.
Then (in section 3.3),
similarities/differences between exploring dynamics of a computational program
in theorem-proving and in a simulation will be reviewed. The intention is to
preview the most straightforward similarities between simulation runs and
explorations in theorem-proving. Direct parallels between the search strategy
called ‘model exploration’ in theorem-proving and generation of trajectories in
simulation will be found.
Section 3.4 will discuss in brief seminal
work for proving in computational models. The initial interpretation-based
exploration of ‘logical models’ in a theory, namely Herbrand’s universe and
Herbrand’s theorem, will be addressed. Herbrand’s theorem is the basis for the
more efficient methods for checking falsity of a set of clauses in first-order
logic. This theorem became the fundamental reference for developing resolution,
the most widely used procedure for proving. This section provides the starting
point for a more comprehensive review of theorem-proving strategies in section
3.5, whose methods are based on these two achievements of Herbrand.
Having presented Herbrand’s foundational
work for theorem-proving in section 3.4, the main strategies for
theorem-proving will be reviewed in section 3.5. It will include a
consideration of the most popular search procedures and strategies in
theorem-proving. Two main branches of theorem-proving approaches will be
presented in accordance with the orientation of their inference procedure,
which might be either predominantly semantic- or predominantly
syntactic-oriented. Simultaneously, examples of theorem-provers using these
procedures and strategies will be offered. First, the syntactic methods will be
presented. These have been the most successful ones. In this group is the
theorem-prover OTTER. OTTER will be used to program the case study of this
thesis and so will be an important reference as a source of ideas for
developing the methodology to be presented in Chapters 5 and 6. This review may
be used to describe the main aspects of OTTER and other theorem-provers found
in the literature. However, neither the simulation method to be proposed in the
next chapter nor the common simulation methods correspond well to a syntactic-driven
proof. Then, the other group of strategies, that consisting of the
predominantly semantic-oriented, will be reviewed (in sub-section 3.5.2). In
this group will be found the so-called model-based exploring approaches and,
among them, tableaux. This sort of search has similarities with the method to
be proposed in the next chapters, but again this method does not fit completely
well in the sort of search described in this sub-section.
However, the given taxonomy, as also happens
with any other given classification, is somewhat arbitrary, as most of the
theorem-provers are in part semantically and in part syntactically oriented.
Hence, it will be worth going further and analysing strategies for
theorem-proving using additional criteria.
To this purpose section 3.6 will be offered.
In this sense, in sub-section 3.6.1 additional criteria for classifying
theorem-provers are given. Then, using the criteria provided so far, the main
aspects of Bonacina’s (1998, 1999) classification are recapitulated in section 3.6.2.
As, once again, neither the proving strategy to be developed in this thesis nor
other simulation methods fit well in the given
(Bonacina’s) taxonomy, a further discussion will be presented in
sub-section 3.6.3.
Having opened the panorama of theorem-proving
strategies, the main aspects of a new tendency in logic-programming -
constraint logic-programming and its variant, rule-based constraint
logic-programming - will be considered
(see, e.g., Frühwirth et al.,
1992). This new area of research seems to be relevant to achieving efficient
methods for exploring dynamics in simulations. There, inference procedures
using a constraint-driven search as an alternative to unification are
implemented. It appears that there, novel and promising ideas for efficient
implementations of exploration of behaviour in a simulation can be found.
Finally, the usefulness of meta-reasoning for
an efficient exploration of the dynamics in a computational program and, in
particular, for implementing context-driven inference procedures will be
highlighted. Context-oriented search seems to be convenient for exploring and
proving theorems in the dynamics of a simulation.
The problem consists in finding a proof
procedure to verify the validity or inconsistency of a formula or a theorem
with respect to a theory. In simulation, a theorem might represent a tendency
in the dynamics of the simulation.
According to some authors (e.g., Chang and
Lee, 1973), such a problem was first tried by Leibniz, then by Peano, and, in
this century by Herbrand’s school. Nevertheless, a general procedure for
proving theorems in a theory was proved impossible by Church and Turing in 1936
(Chang and Lee, 1973). In any sufficiently expressive formal system, there will
always be invalid formulas for which these procedures will never decide. For
example, ‘in certain cases the generation of clauses never stops, because no
finite database satisfies all clauses, but a contradiction does not arise
either. This is because of the ‘undecidability of satisfiability’ (Stickel,
1988). However, there are procedures that are useful for attempting to prove
certain valid formulas.
In logic-programming, a method or program
able to provide an answer (in this case, to the dichotomic question of whether
a formula is satisfiable or not) within a finite delay is called an algorithm,
while those that can provide and answer when such an answer is positive but
there is no guarantee of getting an answer when it is negative, are called
semi-algorithms or procedures (Gochet et al., 1988). Similarly, it is said
that a theory is decidable if it admits a decision algorithm and
semi-decidable, or partially decidable, if it only admits a decision procedure.
Methods for proving the validity of a theorem (e.g., resolution) for
first-order logic are procedures (Gochet et al., 1988).
In consequence, in this chapter the aim is
to discuss appropriate procedures for proving in particular situations. As a
preliminary step towards this goal, the main ways to check the validity of a
theorem with respect to a computational theory will now be reviewed.
According to Chang and Lee (1973, p. 45)
there is no guarantee of finding any procedure to check the invalidity of an
invalid formula. On the other hand, no general procedure exists for verifying
the validity of a valid formula. However, it is always possible to find a
specific procedure for checking the validity of a particular valid formula.
The most important approach for proving
validity of formulas in theorem-proving was given by Herbrand in the 1930s. The
first algorithm for implementing Herbrand’s method was given by Gilmore in
1960. Then, this algorithm was modified, the most important improvement being
that given by Robinson. These algorithms verify the validity of a formula by
detecting inconsistency of the negation of the formula. The important point
here is that: if the formula is valid – and obviously such detection is not
possible - the program will halt after a finite number of steps (Chang and Lee,
1973).
In this thesis the phrase ‘logical model’
will be used to refer to the concept of model in the context of logic. This
will help to prevent confusion, as the notion of model in logic and in
logic-programming is different from the concept of model in modelling and
simulation, which has been used until now in this thesis.
First, some basic concepts will be defined
in order to provide a context for the notion of model in logic-programming
(Gochet et al., 1988). However, only
some notions will be covered and other more basic concepts, such as predicate,
clause, literal, function, term, constant, proposition, unification, and
predicate, will be assumed as known.
Seven terms that will be frequently used
below and have a special significance for understanding the notion of theory
(e.g., that implicit in a simulation) and proofs in a theory are now defined:
Signature: collection of predicate
and functional constants.
Language: set of terms and formulas
generated by the signature through the syntactical rules of predicate calculus.
Structure: relative to a language is
an interpretation of this language.
Theory: relative to a language
is a set of formulas of this language.
Axioms of a theory: that set of
formulas in a language defining the theory.
Theorem in a theory: logical
consequence of the axioms defining the theory.
Logical model of a theory: a
structure for which all formulas of the theory are valid.
A logical model of a theory in predicate
logic might be given with reference to ground terms of the language, that is,
specifying whether each ground term is true or false. Then, the definition of
interpretation given in the semantic specification of the language for
variables and formulas can be used to determine whether a variable or a formula
is valid under a certain logical model or under some interpretation.
Alternative techniques for defining a logical model or a set of logical models
are: specifying only the set of valid ground terms (the remaining ones are
assumed to be false by default), or by a formula. Figure 3.1 illustrates the interrelationship among these
concepts
|
|
Figure 3.1.
Graphic representation
of the relation among the concepts: Language, Signature, Theory, Axioms of
a theory, and Theorems in a theory
|
Example 3-1: Signature: collection of
predicate and functional constants.
Signature: P( , ), Q( , ), R( )
Language: any formula A ¦ B, where A
can be P, Q, or R valued on certain variables, and ¦ can be any
of the operators commonly used in the literature for defining a propositional
first-order logic {v, ʌ,
…}
An example of a theory is S = {(1)~ P(x,
y) v ~ Q(y,z) v R(x), (2) P(x,y) v R(y,z), (3) Q(x.y) v R(x)}
A theorem for this theory is R(x).
Assuming a propositional language, S = {(1)~
P v ~ Q v R, (2) P v R, (3) Q v R}:
An interpretation (signature) would be {R = Q= true, P = false}
The formula R can be used to represent the
set of logical models M = {R = true, Q = V1, R = V2}
where V1 and V2 are in the domain {false, true}.
In general, a logical model search procedure
for proving is an interpretation-guided exploration of logical models. An
example of a logical model search using backward-chaining is tableaux. Also,
forward-chaining logical model procedures have been implemented, for example
event-driven simulation and partitioning of rules in some declarative MAS, as
will be seen below.
Logic-programming and theorem-proving can be
applied to many research subjects. In this thesis its particular interest is
its use for proving tendencies in the dynamics of a simulation. To make clear
the relation between simulation on the one hand and, logic-programming (and
especially theorem-proving) on the other, the relevant aspects of the dynamics
of a simulation and inference procedures in logic-programming and
theorem-proving will be reviewed. The main similarity is found between what in
simulation is called a ‘trajectory’ and what in logics is called the logical
model of a theory.
A trajectory of a simulation corresponds to
a logical model or valid interpretation of a theory in logics. In fact, the
generation of trajectories in a simulation can be seen as a particular case of
logical model generation. It is a generation of logical models for the theory
represented by the simulation program. However, it is not always required to
know all valid facts in a logical model, as is the case in tableaux, in order
to check theorems in a trajectory. A simulation implemented using declarative
programming will be expressed in terms of clauses and there may exist alternative
ways of generating logical models corresponding to the different possible
simulation trajectories. A formula will be a theorem of the simulation program
if it is true in all simulation trajectories. A semantic proof of certain
regularity in a simulation can be implemented by generating all trajectories
and observing whether the regularity holds in all of them (this is a ‘logical
model checking’). This assumes that, as is common in simulation, a finite-state
structure representing all logical models exists.
Simulation trajectories are usually
generated following an event-driven or at discrete, equally spaced intervals of
the independent variables. This is the general case, for example, in MAS and
finite difference methods for solving differential equations. Its generation
usually consists in a time- and/or space-driven generation of states starting
from a certain initial state. This is a sort of forward-chaining inference. For
instance, in the simulation of a differential equation, the simulation might
follow a temporal and/or a spatial order. Consider, for instance, the case of a
two-space heated plaque whose temperature at the internal points changes over
time and is different for different points. The differential equation might be
like this:
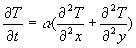 ; where: T
represents the temperature, x and y are the spatial variables,
and t represents time. These sorts of equations are solved using finite
differences: the partial derivatives are replaced by finite difference
approximations, then a set of finite values in the range of interest is chosen
for the independent variables x, y, and t, and, finally, T
is obtained for the chosen points of the independent variables step-by-step,
starting from the known values of T in the boundaries of the plaque. Should
this flux be null, time is no longer a variable of interest, although it may
still be interesting to know the plaque’s temperature at each point; then the
simulation steps would only be over the spatial edges. In this case the
simulation steps follow only a spatial sequence. In the case of the simulation
of processes involving humans (for example, simulation of a queue system in
industry, in a road, or in a bank, or simulation of social interaction in a
market), the dynamics is usually carried out following a temporal sequence.
; where: T
represents the temperature, x and y are the spatial variables,
and t represents time. These sorts of equations are solved using finite
differences: the partial derivatives are replaced by finite difference
approximations, then a set of finite values in the range of interest is chosen
for the independent variables x, y, and t, and, finally, T
is obtained for the chosen points of the independent variables step-by-step,
starting from the known values of T in the boundaries of the plaque. Should
this flux be null, time is no longer a variable of interest, although it may
still be interesting to know the plaque’s temperature at each point; then the
simulation steps would only be over the spatial edges. In this case the
simulation steps follow only a spatial sequence. In the case of the simulation
of processes involving humans (for example, simulation of a queue system in
industry, in a road, or in a bank, or simulation of social interaction in a
market), the dynamics is usually carried out following a temporal sequence.
Similarly to what happens in simulation,
many logic-based computational systems follow a forward-chaining strategy.
Consequences are generated as the antecedent of inference rules match facts
already existing in the database. This is a strategy also used in
theorem-proving. Generations of trajectories over time or in temporal logical
model exploration have been formalised in Temporal Logics. See, for example,
Fisher et al.’s proposal of a clausal
resolution procedure for discrete temporal logic (Fisher et al., 2000). Obviously, theorem-provers that use forward-chaining
inference have similarities with simulation.
A common strategy for proving in
computational models, which is extendible to simulation, is to add the negation
of the theorem into the database and then show that this causes a
contradiction. A drawback of this sort of search is that many irrelevant facts
(for the proof) may be generated before the contradiction appears. To handle
this problem, heuristic strategies have been developed. More details about
these procedures will be given below.
In contrast to this, searches in
logic-programming (e.g., in Prolog) are not usually forward-chaining but
backward-chaining or goal-driven. A goal is managed as a question to be answered
with respect to new goals or facts. Assume this is a goal at level 1. If this
goal matches the head of a rule (consequent), the body (antecedent) of the rule
(with the respective update of the variables according to the variable
unifications) becomes the new goal in a next level (level 2). This new goal
might consist in a conjunction of predicates. In this case, each of those
predicates would be a sub-goal to be satisfied at the new level – thus, a new
list of sub-goals is constructed. The next task is to check if each of these
goals is satisfied. Then, one of them is taken as the goal to be treated. Once
the head of a rule matches this sub-goal, then a new list of sub-goals at
another level (level 3, given by the antecedent of the matching rule) is set.
The search stops as soon as all resulting goals become true, that is, as soon
as all the goals are shown to be facts.
If during that search new sub-goals have
priority over previous target-goals to be tested (e.g., goals are listed in
order LIFO: Last-In First-Out), the search is called depth-first. On the other
hand, if new sub-goals are considered only after previous target goals (e.g.,
goals are arranged in order FIFO: First-In First-Out), the search is called
breadth-first. Generally a depth-first search generates less data than a
breadth-first-search. It is the search commonly implemented in
logic-programming (e.g., in Prolog).
Despite these differences in how the
inference is driven, the inference procedures in both logic-programming and
resolution-based theorem-provers are variants of the semantic and syntactical
methods to be explored below.
To summarise, in some aspects simulation is
closer to logical model generation in logic-programming and theorem-provers
than to logic-programming languages such as Prolog, as those procedures and
simulation usually follow forward-chaining inference procedures while Prolog’s
inference procedure works in backward-chaining. On the other hand, however,
simulation also has similarities with certain backward-chaining search
procedures like tableaux, as they both follow a logical model generation
strategy. Accordingly, in principle it seems convenient to try proving in
simulation using procedures already implemented in forward-chaining
theorem-provers and in logical model generation. Nevertheless, syntactic
backward-chaining methods appear attractive to lessen certain problems (e.g.,
the huge amount of accumulated data) appearing when implementing logical model
generation and forward-chaining methods. A recently developed approach is
constraint logic-programming, which seems promising because of its flexibility
for driving the search by exploiting semantic information in the data rather
than using only traditional unification. Aspects of this approach will be
utilised in this thesis as the methodology to be proposed in Chapter 5 consists
in certain constraint-based explorations of trajectories.
The first attempts for checking the
unsatisfiability of a set of clauses before, in the next section, going on to
those commonly used in theorem-proving will be presented in this section. It is
common to attempt to prove the unsatisfiability of clauses. A theorem is proved
by showing that its (classical) negation is unsatisfiable.
The barest procedure for proving the falsity
of a set of clauses S is to check if they are false under all possible
interpretations of the theory. Evidently, there might be a huge number of
possible interpretations making this task impossible. This is only realistic in
a few cases and not in those of interest in this thesis.
Notice that this procedure is not syntactic
but semantic. Each interpretation for which a theory is valid is a logical
model of the theory. Other approaches for proving based on interpretations will
be reviewed in section 3.5.
In order to improve the previous procedure,
it seems convenient to find a sub-domain SD of all possible domains D of clause
interpretations, so that, to know if a set of clauses S is unsatisfiable, it is
necessary and sufficient to check the interpretations of S in SD. The first
answer came from Herbrand and the sub-domain is called Herbrand universe
of S (for more details, see Chang and Lee, 1973; Wos, 1988; Gochet et al., 1988). Chang and Lee (idem, p. 52) define it in this way:
‘Let
H0 be the set of constants appearing in S. If no constant
appears in S, then H0 is to consist of a single constant, say
H0 ={a}. For i = 0, 1, 2, … let Hi+1 be
the union of Hi and
the set of all terms of the form fn(t1, …, tn)
for all n-place functions fn occurring in S, where
tj, j = 1, …, n, are members of the set Hi. Then
each Hi is called i-level n constant set of S, and
H¥, or limi®¥ Hi, is called the Herbrand
universe of S.’
Examples:
a) if
S = {P(a)}, then H0 = {a};
b) if
S = {P(a), P(f(x)), Q(g(y))}, then
H0
= {a};
H1={a,
f(a), g(a)};
H2=
{a, f(a), g(a), f(f(a)),f(g(a)), g(f(a), g(g(a))};
H2=
{a, f(a), g(a), f(f(a)),f(g(a)), g(f(a), g(g(a)),f(f(f(a))),… }.
Instances of a clause C obtained by
replacing variables in the clause C by members of the Herbrand universe
are called ground instances. In the second example above, P(g(a)) and
P(f(g(f(a)))) are examples of ground instances of clause P(f(x)).
However useful Herbrand universe is, it is
usually hard to check all interpretations over it because it is still too big.
Further steps toward more useful procedures were encouraged by Herbrand’s
theorem. Chang and Lee offer a version of it:
Herbrand’s Theorem. A set of clauses
S is unsatisfiable if and only if there is a finite unsatisfiable set S’ of
ground instances of clauses of S.
The importance of the theorem is that it
will be sufficient to have a finite set S’ of unsatisfiable ground
instances of S to know that the whole set S is unsatisfiable. This
theorem has become fundamental for developing resolution, the most widely used
procedure for proving. The main difficulty for applying this theorem is the
requirement of ground clauses. A resolution goes forwards; it has to be applied
not only over grounded clauses but also over ungrounded ones (Chang and Lee,
1973).
In this section some of the main approaches
in theorem-proving will be considered. First, those implementing
syntactic-driven procedures based on clause manipulation will be outlined,
followed by those that are semantic-driven since they are founded in logical
model generation. Among the resolution methods and heuristics to be listed
below, there were used in the examples presented in this thesis (see Chapter
7): hyperresolution, the set of support strategy (a particular case of semantic
resolution), subsumption, fewest-literal preference strategy, and demodulators.
Other, alternative methods currently used in theorem-proving or in declarative
programming will be presented.
The great advantage of resolution is that it
can be applied over clauses having variables. Therefore, the size of the
universe of clauses over which it works is usually smaller than when using
Herbrand’s universe while the number of interpretations to be considered is
still the same. Actually, as resolution can be applied over clauses having
variables, many or even an infinite number of interpretations can be considered
at a time.
Resolution-based theorem-proving has become
a very important area of research since 1965, after the introduction of
resolution by Robinson (Chang and Lee). Further refinements and search
strategies have been developed, e.g.: hyperresolution (Robinson himself),
semantic resolution (Slagle), the set of support strategy (Wos, Robinson, and
Carlson), lock resolution (Boyer), and linear resolution (Loveland, 1970;
Luckham, 1970) (more details will be given below).
Many successful resolution-based
theorem-provers have been developed. One to be used in this thesis is OTTER
(see McCune, 1995; also see www-unix.mcs.anl.gov/AR/otter/).
The important point in Robinson’s resolution
principal is that it generates a new clause from two existing ones. The
generated clause will replace the two existing clauses. Then, Robinson’s
resolution, also called binary resolution because it uses two clauses to
generate the new one, can be seen as an inference rule (Wos et al., 1988). In fact, binary
resolution can be applied in different forms; for example, it can be seen as a
generalisation of the inference rule that gives (P or R) from: (P v
Q) Ù (~Q v R). Moreover,
it can be considered as a generalisation of ‘modus ponens’ and ‘syllogism’
(Wos, 1988). Applying it iteratively, a chain of clauses can be generated. If
the original set of clauses is inconsistent, then a contradiction occurs in the
chain - this is called the completeness of the method. Binary resolution is
complete. Obviously, completeness is a desirable attribute for resolution
methods. If the set of clauses is satisfiable (there is no proof), binary
resolution will halt once no more clauses can be generated. Nevertheless,
complete proofs methods are only available for a restricted range of relatively
inexpressive logics.
The main advantage of binary resolution is
that it is complete and that it does not put restrictions on either of the
resolvents. So it is one of the most generally applicable resolution variants.
However, it might be inefficient in the sense that other resolution methods
might do certain proofs in shorter manner in terms of time or generated data.
Moreover, other resolution procedures might be more recommendable in certain
situations, for instance, in keeping with the characteristics of the clauses
over which the proof is going to be executed. For example, when translating a simulation
program into a theorem-prover, it may be convenient to see the original data of
the simulation program (e.g., that given the initial state) as unit clauses and
the rules of the simulation program as multi-unit clauses and then apply
hyperresolution (see below) in the search so that the multi-unit clauses
operate as the inference rules (see below and Wos, 1988). Sometimes,
theorem-provers allow the user to choose the resolution method(s) to be
applied.
In the following some alternative resolution
methods will be informally reviewed as some of them are used in the
theorem-provers of interest in this thesis, e.g., in OTTER. Then, the different
strategies used together with resolution for improving the search in a
theorem-prover will be considered. These strategies are heuristics aiming to
make the search shorter and computationally less expensive.
Semantic resolution is one of the first
improvements over binary resolution in the search for methods to decrease the
number of redundant clauses.
The main idea is to divide the set of
clauses S into two subsets S1 and S2, preventing resolution within clauses in a
subset. This can be explained by using an example from Chang and Lee:
Example 3-3.
S = {(1)~ P v ~ Q v
R, (2) P v R, (3) Q v R, (4) ~R}
Applying binary resolution to (1) and (2), it is found that R1
= ~ Q v R, from R1 and (3) is obtained R2 = R, and from R2
and (4) it is concluded that the set is unsatisfiable. Binary resolution has
been applied using clauses in the following order: (1), (2), (3), (4). The same
result is achieved if binary resolution is applied in the order (1), (3), (2),
(4). Though this new inference is clearly redundant, an automatic program might
produce it if not prevented. Note that binary resolution might give even more
redundant information; for example, from (1) and (4) a useless resolvent is
obtained in the direction to prove the unsatisfiaility of S. Some of
these redundant inferences are prevented by refinements of resolution
procedures, as will be seen in this and in the coming sections.
Using the interpretation I = {~ P, ~ Q, ~
R}, the set of clauses can be separated in two subsets: S1 the subset of
satisfied clauses and S2 the subset of unsatisfied clauses. That is, S1 =
{(1) ~ P v ~ Q v R, (4) ~ R}, S2 = {(2) P v R, (3) Q v R}. This
prevents (1) being resolved against (4). However, (1) can still be resolved
with (2) and (3), taking clauses in S in a different order. To prevent
resolving clauses in different orders when the result is the same resolvent, an
additional tactic is used: ordering of predicate symbols. Assume the order P
> Q > R is used. Given priority to predicates of higher order,
binary resolution will be applied in the sequence (1), (2), (3), (4). In fact,
this ordering is arbitrary and semantic resolution can be considered as an
inference rule applied simultaneously over several clauses, in this case over
(1), (2), and (3). As (1) is used to match both (2) and (3), it is called the nucleus,
while (2) and (3) are called satellites. Semantic resolution is
complete (Chang and Lee, 1973).
Chang and Lee give the following formal
definition for semantic resolution. It is reproduced to add clarity in the
exposition and because of its usefulness for defining other resolution variants
to be set in the next sections. Note that Chang and Lee name the resolvent semantic
clash (Chang and Lee, 1973):
‘Let I be an interpretation. Let P be
an ordering of predicate symbols. A finite set of clauses {E1, …,
Eq, N}, q ≥ 1, is called a semantic clash with respect
to P and I (or PI-clash for short), if and only if E1,
…, Eq (called the electrons) and N (called the nucleus)
satisfy the following conditions:
1. E1,
…, Eq are false in I.
2. Let
R1 = N. For each i = 1, …, q, there is a resolvent Ri+1
of Ri and Ei.
3. The
literal in Ei, which is resolved upon, contains the largest
predicate symbol in Ei, I = 1, 2, …, q.
4. Ri+1
is false in I.
5. Rq+1
is called a PI-resolvent (of the PI-clash {E1, …, Eq,
N}).’
Observe
that if the nucleus is valid over the chosen interpretation, then the
satellites are false, and vice versa.
Also, it is important to notice that an application of semantic resolution as
an inference rule does not need to have intermediate steps; that is, it can be
thought of as applying simultaneously over the nucleus and the satellites. Here
its usefulness is in reducing several inference steps into one step. This might
also turn out to be a reduction in redundant data.
Additional refinements have been proposed
over semantic resolution, for example, ordering of clauses. Some of them have
turned into other variants of resolution, such as lock resolution.
Nevertheless, some of those procedures are not complete (e.g., semantic
resolution with ordering of clauses) or have disadvantages when implemented
automatically. In the coming sections, some of the more successful variants of
semantic resolution will be examined.
Positive (negative) hyperresolution is a
special case of semantic resolution where the interpretation is chosen as that
with all literals negative (positive). As a consequence, all satellites will
contain only positive (negative) literals and the nucleus will contain at least
one negative (positive) literal, and yield (if successful) a clause with only
positive (negative) literals. Hyperresolution will be the resolution method
chosen in OTTER for carrying out the exploration of the dynamics of the model.
Example 3-4
Considers S as given in example 3-3, i.e., S
= {(1)~ P v ~ Q v R, (2) P v R, (3) Q v
R, (4) ~R}, (1) is the nucleus, (2) and (3) are the satellites, and I =
{~P, ~Q, ~R}. It is a case of
positive hyperresolution: literals in the interpretation are all negative, the
nucleus has at least a positive literal (R), all literals in the satellites are
positive, and the resolvent is positive (R).
Though this is understood as a strategy, it
is presented here because it can be considered as a special case of semantic
resolution. The set of support strategy was proposed by Wos, Robinson, and
Carson (Wos et al., 1965). It is a
very successful strategy and has been adopted as the main strategy in many
theorem-provers (e.g., OTTER).
It consists in a division of the set of
clauses to two groups, as in any other variant of semantic resolution. The
first of these will be a set of valid clauses and the second a set of
unsatisfiable clauses. There are several ways to make this division. For
example, if we wanted to prove that the theorem T is valid in the theory
given by the set for clauses {A1, A2, … ,An}, the aim
would be to prove that A1ʌ A1ʌ A2ʌ … ʌ An ʌ ~T is
unsatisfiable. The first and second sets to be S1 ={A1, A2, … ,An} and S2
= { ~T } might have been chosen.
In theorem-provers such as OTTER, the set of
valid clauses, called set of support (‘sos’!), is chosen as the set of
facts the user can easily recognise as valid and the other subset, called usable
set, is chosen as the rest of the clauses including the negation of the
theorem. For example, the sos might contain those facts given the
initial state in a simulation and the usable set might be given by the
remaining clauses in the original set of clauses S and the negation of the
theorem. Clauses in the set of usable may be used as the nucleus for
hyperresolution or/and as inference rules. In OTTER no inference is allowed
using only clauses from the list usable –at least one clause should come from
the list sos.
The set of support
strategy is complete (Chang and Lee, 1973). However, when
combined with hyperresolution, ‘completeness is not guaranteed’ (Wos et al.,
1988, p. 436).
In the example to be
given in Chapter 7, the rules to run the simulation will be translated as
clauses and placed, along with the negation of the theorem to be proved, in the
set of usable. Data in the simulation language will be placed as ground
instances in the sos.
Linear resolution was proposed by Loveland
(1970) and Luchham (1970). It later underwent several improvements (according
to Chang and Lee, 1973): ‘that given by Kowalski and Kueher (1971) and that by
Loveland (1972) which is more important for computational implementations.’
Linear resolution starts with two clauses (C0
and B0) given the resolvent (C1). Then C1
is resolved against another clause B1 to get C2.
Afterwards, the new clause is resolved against clause B2 to
get another resolvent C3. This procedure is continued until a
contradiction or the empty clause appears (if the proof is successful). The
basic characteristic of the ‘chain’ of clauses generated by the linear
resolution procedure is that the resolvent in one step is used as one of the
clauses to be resolved upon in the subsequent step. Linear resolution is
complete (Chang and Lee, 1973).
The already described depth-first and
breath-first searches are particular cases of linear resolution (Chang
and Lee, 1973). Linear resolution style search has been popular in
logic-programming (e.g., depth-first search in Prolog) and in theorem-proving
when using tableaux. It seems more closely related to backward-chaining search
than to forward-chaining search.
In this subsection some of the more popular
strategies for driving the inference procedure in (syntactic) theorem-provers
and, in particular, implemented in OTTER will be discussed. The main role of
these strategies is to choose, among the commonly huge amount of possible
deductions and ‘path searches’, those that hopefully will lead to the proof
with less data generation, or at least preventing as far as possible the
generation of useless data.
·
Deletion Strategy or Subsumption
The idea is to eliminate copies of the same
clause or clauses that are instances of other clauses. ‘The clause A subsumes
the clause B when there exists an instance A that is a subclause [an instance]
of B’ (Wos, 1988).
Subsumption can be trivial or as complicated
as may be wanted. A trivial case is P(x) subsuming P(a), where a
is a constant and x is a variable. A more complicated case is P(x)
subsumption of P(a) v Q(b), where a and b are constants
and x is a variable. In this case, if P(x) is true for any x,
P(a) is also true and then P(a) v Q(b) is true, whatever happens
with Q(b).
·
Fewest-literal Preference Strategy
When using resolution procedures such as
hyperresolution and UR-resolution, for different reasons it is convenient to
have clauses with few literals. The main reason is that it is easier to resolve
the clause with others successfully. Another motive is that usually the theorem
to be proved has few literals (generally one).
Its advantages are clear, for instance, when
using it along with hyperresolution and the set of support strategy. For
example, in OTTER, when applying hyperresolution, clauses in the sos are
used as satellites while those in the set of usable are used as the
nucleus. The shorter the number of
literals of those chosen as satellites, the easier it will be to apply
hyperresolution.
Some theorem-provers (e.g., OTTER) implement
this strategy by giving each clause a weight proportional to the number of
literals, after which clauses are ordered and then selected according to this
weight.
·
Heuristic-Evaluation Function
This consists in giving each clause a weight
as a function of certain clausal features such as a number of literals and a
number of distinct variables. Usually the function is a weighted linear
combination of these features. The difficulty with this procedure is in
calculating appropriated weights. Because of this, it is not implemented in
theorem-provers. As can be seen, fewest-literal preference strategy is a
particular case of heuristic-evaluation function.
Usually, theorem-provers implement a
weighting heuristic, giving the user the option to specify the criterion
for clause weighting.
·
Demodulators
Demodulators are procedures ‘to simplify and
canonize information’. (Wos et al., 1988). Clauses giving
semantically redundant, though not necessarily syntactically redundant,
information are discarded. The main idea is to rewrite terms in a clause. For
example, SUM(1,2) and 3 are terms giving the same though
syntactically different information. As 3 is ‘simpler’, it would be a
candidate to canonise this and other numerical expressions semantically
equivalent (e.g., MULTIPLY(3,1)). It would be used to rewrite semantically
equivalent expressions.
Demodulators are very useful for doing
numerical manipulations. For example, a demodulator in automated reasoning
languages and theorem-provers (e.g., OTTER) might be: SUM(x,y) = x + y.
Here ‘+’ has the meaning of the numerical operation addition, while SUM
is a predicate symbol. Once the predicate SUM is used in a term, the
demodulator is called, then a sub-program, doing the numerical operation is
called, and, finally, the result of the addition is sent back to rewrite the
term. The usefulness of demodulators in simulation is obvious, as numerical
operations are common. However, there are few theorem-provers offering
demodulators, among them OTTER. In theorem-provers implemented over Prolog,
such as SETHEO, numerical manipulations can be achieved using Prolog
facilities. Demodulators will be used in the example (given in Chapter 7) for
implementing functions originally written as backward-chaining rules in SDML.
Consider
a more complicated example of demodulation taken from Wos et al. (1988). It can be checked that the following two predicates
have the same information:
EQUAL(sum(sum(x,v),sum(y,z)),sum(sum(x,y),z))
EQUAL(sum(x,sum(y,z)),sum(sum(x,y),z))).
EQUAL is a literal interpreted as
meaning equal.
In general, a demodulator has the form D:
EQUAL(r,s), where r and s are terms. If a clause C has
a term t matching r and the result of the matching is r’(r’
= t), then applying the demodulator D to C will result in
replacing C by C’ given by the substitution of t for s’,
where s’ results from the appropriated instantiation of the demodulator D’:
EQUAL(r’,s’). The demodulator given above for SUM can be thought as EQUAL(SUM(x,y),
x + y).
·
Paramodulators
Paramodulation has some similarities with
demodulation, though it is very different. Paramodulation generates a new
clause C from two clauses A and B, while demodulation
replaces and subsumes an old term for a new one.
Concretely, should we have the clause A
with an equality literal, lets say EQUAL(r,s), and clause B with
a term t matching, for example, the left side of this literal, r,
then the matching, where r’ = t, gives the instances A’, B’, and EQUAL(r’,s’)
(for the clauses A and B and the EQUAL literal,
respectively). Call K’ the literal EQUAL(r’,s’) and B’’ the clause B’,
where r’ has been replaced by s’. Then the resulting clause C of
applying paramodulation to A and B using the EQUAL literal
(EQUAL(r,s)) of A and the term t in B, will be the
disjunction of A’-K’ and B’’.
Example 3-5
Consider A = P(x) v
EQUAL(PROD(x,0), 0)) , and B = Q(x) v
R(PROD(2,0)),
Where:
r = PROD(x,0), s = 0; t = PROD(2,0)
Applying the explained procedure it will
give:
r’ = PROD(2,0), A’ = P(2) v
EQUAL(PROD(2,0),0), B’ = Q(2) v R(PROD(2,0)), K’ = EQUAL(PROD(2,0),0), B’’ = Q(2) v
R(0).
Finally, the disjunction of A’ – K’
and B’’ gives:
P(2) v Q(2) v R(0).
If A were A = EQUAL(PROD(x,0),
0)), the result would have been Q(2) v R(0).
As was stated above, forward-chaining search
consists in applying resolution rules over the clauses in the database,
generating consequences that are added to the database if they are not subsumed
by clauses already existing in the database. This process is repeated
iteratively until a certain stopping condition is found (for example, a
contradiction or an empty clause) or it is not possible to generate more
consequences. Forward-chaining is the ‘counterpart’ of backward-chaining.
·
Example: OTTER, a first-order logic theorem-prover
OTTER is the theorem-prover used in this
thesis for implementing a MAS simulation case (see Chapter 7), and so it will
be a source of ideas for the methodology to be presented in the next chapters.
Two reasons for using OTTER in this thesis are: first, because it is one of the
most successful theorem-provers, and second, because it offers facilities for
data manipulation (e.g., demodulators). This is convenient for implementing
cases like the example from social simulation given in Chapter 7. This example
is about a trader-distributor interaction, where numerical manipulation is
made, e.g., for calculating sales, orders, prices. Other theorem-provers are
very restricted to symbolic manipulation and do not provide these sorts of
facilities.
OTTER is a forward-chaining theorem-prover
that uses a set of support strategy. That is to say, the original set of
clauses is separated in to two groups, a first one containing only valid
clauses called set (list) of support and a second group of (assumed) unsatisfiable clauses called
usable list (this set of clauses is unsatisfiable if the theorem is valid). The
usable list contains those clauses to be used as inference rules and the
negation of the theorem to be proved.
OTTER offers a wide range of inference rules
and strategies, which can be turned on and off by using commands. Among the
inference rules OTTER offers are: binary resolution, hyperresolution, unit
resolution, and UR-resolution. The strategies it presents include: weighting
and subsumption.
OTTER also offers demodulators and
paramodulators. These are very helpful in certain applications. In simulation,
numerical manipulations and rewriting is not only a factor of efficiency but it
also becomes essential in practice. In OTTER demodulators are applied as rules
in backward-chaining whose intermediate or partial consequences are not written
in the rulebase. They work as functions in imperative programming, in the sense
that they are called with a set of parameters and then they return the
corresponding result. For example, a demodulator could simply be a function to
multiply two integers: MULT(a, b) = a * b (for more about demodulation
and paramodulation, see above).
OTTER main inference procedure works as
follows (McCune, 1995):
‘The main loop for inferring and processing clauses and searching for a
refutation operates mainly on the lists usable and sos:
While (sos is not empty and no refutation has been found)
1. Let given_clause be the `lightest' clause in sos;
2. Move given_clause from sos to usable;
3. Infer and process new clauses using the inference
rules in effect; each new clause must have the given_clause as one of its
parents and members of usable as its other parents; new clauses that pass the
retention tests are appended to sos;
End of while loop.7
... Otter's main loop implements the
set of support strategy, because no inferences are made in which all of the
parents are from the initial usable list.’
In
step 3., the retention test checks that the new clause is not
subsummed for existing clauses.
A
difficulty when using most of the existing theorem-provers is their poor
interaction with the user, and OTTER is not an exception. In McCune’s (1995)
words: ‘Although Otter has a primitive interactive feature … it is essentially
a noninteractive program. On unix-like
systems it reads from the standard input and writes to the standard output:
otter
< input-file >
output-file
No command-line options are accepted; all options are given in the input
file.’
As has been said, for implementing an
example in OTTER in Chapter 7, hyperresolution, the sets of support and usable,
subsumption, fewest-literal preference strategy, and demodulators will be used.
However, when re-implementing the example in SDML, the search strategy will be
model-driven by using automatic partitioning of the set of clauses and other
strategies SDML offers, which are more common in simulation and in logic-programming
languages than in theorem-provers (see next section, especially sub-section
3.6.3).
The inference procedures in this section are
based on a search over interpretations as opposed to clausal manipulation studied
in the previous paragraph. Aspects of semantic-driven search were already
considered in brief when considering semantic resolution, but there the use of
interpretations was restricted to separate clauses in groups. The procedure is
still predominantly syntactic as it is based on clausal manipulation after the
separation is made. In the methods to be reviewed in this section,
interpretations are more intensively used to drive the search. In fact, each
inference step is guided by the validity of certain terms.
Recent theorem-provers have been developed
using the notion of semantic search, particularly using tableaux. Comparing
with interpretations where all possible interpretation have to be checked,
tableaux are more efficient as it considers only those interpretations that
might make valid (literals in) certain clause(s) - in this sense it is also
guided by clauses.
Tableaux generate indirect proofs as ‘the
premises of an argument form together with the negation of the conclusion are
tested for joint satisfiability’ (Gordon et
al., 1992). ‘ … In essence, a tableau is a survey of the possible
interpretations of S with each branch representing an interpretation’
(Bonacina, 1999). Tableaux are an ‘attempt to systematically construct a
structure from which a logical model can be extracted for the negation’ of the
theorem to be proved (Fisher et al.,
2000).
The idea is to generate a branch for each
possible valid interpretation. Once a contradiction appears in a branch, this
branch is closed. If all children of a node are closed, the node is also
closed. If a branch is not closed (there is no contradiction in it), it is said
to be open. An open branch, where no more inferences can be made, offers
a logical model of the theory (remember, the theory in this case is
given by the conjunction of the premises and the negation of the theorem). In
this case the whole set of clauses defining the theory is satisfiable, the
theorem is valid, and the negation of the theorem is false. On the other hand,
if all branches of a tableau are closed, then there is no valid interpretation
and the theorem is valid.
The set of braches gives the tableau. If at
least one branch is open, it is said that the tableau is open. If all branches
are closed, the tableau is closed. As an (tableaux) inference rule (an example
of this sort of inference rule will be given below) is applied, there is a
transition from a tableau (state of the search) to another tableau (next state
in the search). The proof will be successful if a final state with a closed
tableau is reached. As soon as the procedure generates an open branch where no
more inferences can be made, the proof fails. Tableaux are complete.
Now logical model elimination tableaux
will be explained as an example of inference procedures used in tableaux.
Starting from the set S, defined as the union of the premises and the
negation of the theorem to be proved, roughly the inference procedure works as
follows (Bonacina, 1999):
Assume the starting clause is Ci =
L1 v L2 …v Ln. This gives a first state in
the search represented by a tableau with Ci as its unique
node. A branch named Lm is created for each literal Lm
of Ci representing the different ways this clause can be
satisfied. Then suppose there is another clause in S: Cj = F1 v F2
v … Fk, and that for the substitution σ: -L1σ
= F1σ. Then this clause Cj will be added
at the node corresponding to branch L1, closing the branch
for F1 and applying σ to literals in branch L1.
(As is known, it is possible to apply binary resolution to these two clauses,
giving as resolvent the disjunction: (L2 …v Ln v F2
v … Fk)σ). This gives a new state in the search process:
the original tableau with node Ci expanded by this second
node Cj which has branch F1 closed,
and the application of the substitution σ. Repeating this procedure to the
remaining literals in nodes for Ci and Cj,
the inference proceeds. A final state is achieved either because an open branch
where no more inferences can be made is found (a logical model for S given by
this branch has been found, the negation of the theorem is valid in this
logical model, and the proof fails) or the tableau is closed (the proof
succeeds).
Example 3-6.
Assume, S = {(1)~ P v ~ Q v R, (2) P v R, (3) Q v R, (4) ~R}, where the
premises and the theorem are clauses (1)-(3) and (4) respectively, a possible
tableau is shown in Figure
3.2.
|
|
Figure 3.2. A tableau for example 3-6
|
Two theorem-provers written as extensions of
Prolog will be considered: SATCHMO: SATisfiability CHecking by [logical] MOdel
generation; and PTTP, a Prolog Technology theorem-prover. Both of them are
based on logical model search. Their most relevant aspects will be considered.
First, common characteristics will be enumerated and then particular aspects of
SACHTMO will be reviewed, as it presents more similarities with OTTER and the
way an exploration of simulation trajectories using SDML’s facilities will be
implemented.
In both of them result from attempts to
extend Prolog with a complete procedure to manage non-Horn clauses (i.e., not
only Horn clauses as is usual in Prolog). A difference between them is that
while SACHTMO is written on top of Prolog, PTTP is an extension compiled along
Prolog’s source code. To be implemented on top of Prolog gives SATCHMO
flexibility and portability. Both are tableaux-style implementations. They
introduce additional inference procedures from those Prolog has, are semantic
oriented, and use splitting and backtracking to generate alternative paths in
the search.
SATCHMO is based on the introduction of a new
set of rules in order to be able to manage clauses not allowed in Prolog.
These rules are fired in a forward-chaining manner. In fact, the primary idea for
writing SATCHMO comes from the observation that range-restricted clauses can be
exploited by the inference procedure. A range-restricted clause is a clause
such that every variable occurs in at least one negative literal. If a clause
is written in the form of a rule with the negative literals in the antecedent,
it is said that the clause is range-restricted if every variable is in at least
one literal in the antecedent. Then, the idea is that if in the rule a implies b (or in the clause ~a | b),
a is valid but b is not, then b can be taken as deducted via this
rule and added to the database.
SATCHMO is based on hyperresolution.
Splitting and backtracking are introduced in SATCHMO by allowing disjunctions
in the consequent of rules. Other problems Prolog’s search faces are also
solved: the difficulty of infinite generation of clauses due to recursive
clauses as a consequence of unbounded search is worked out by using subsumption
(Rainer et al., 1988).
A drawback of SATCHMO is that
range-unrestricted clauses might need full instantiation of some variables over
the whole Herbrand, universe which might lead to an ‘explosion’ in the number
of ground instances. This is prevented by an appropriate transformation of
range-unrestricted clauses into range-restricted clauses, which is always
possible. See, for example, CPUHR tableaux, which are an adaptation of PUHR:
Positive Unit Hyperresolution tableaux (Bry et
al., 1996), the tableaux used to formalise SATCHMO, for managing
constraints and existentially quantified variables (Abdennadher et al., 1997).
A logical model in SATCHMO is given by a set
of ground terms, more concretely by those ground terms that are satisfied in
the logical model (the remaining ones are assumed violated by default). This
notion of determining all facts in a logical model is slightly different in
simulation and especially so when proving tendencies due to practical reasons.
For example, not all facts of a trajectory are generated when searching for a
tendency; once the tendency is found in the trajectory, the program backtracks
leaving the remaining facts (irrelevant for the proof) as unknown.
The classification will be based on the
character of the search, which might be:
1. Forward-
vs. backward-chaining (i.e., assumption expansion vs. sub-goal reduction)
As is already known, in forward-chaining the
precedent of a rule is checked and, if it matches the database, then the rule
fires and the consequent with the corresponding instantiations of variables is added
to the database. In case of disjunctions in the consequent, different branches
will appear, each one labelled with an assumption. On the other hand, if the
search is backward-chaining, the consequent of a rule is checked and, if the
goal is a conjunction of several sub-goals, a branch is open to check each of
them. In this case, the sub-goals label the generated branches.
2. Semantic
vs. syntactic focused: interpretation- vs. clausal-driven search
Resolution is basically syntactic or clause
oriented; it generates a clause from several other clauses considering
basically the form of the clause and the meaning of terms (see above).
Alternatively, tableaux are in essence semantic oriented, as the generated
branches in a node are precisely those alternative interpretations that make
certain clauses valid.
3.
Implicit vs. explicit splitting of the search
space
Optional solutions in the search may appear
for different reasons, for example, owing to a disjunction in the antecedent
and/or in the consequent of a clause, or owing to existentially quantified
variables in the consequent (see, for example, Abdennadher et al., 1997). In a splitting search, one branch is investigated at
a time. This sort of search will be called explicit search. In this case, if
attempting to prove unsatisfiability, the program backtracks once a
contradiction appears in a branch. Alternatively, in an implicit search the
inference is carried out over all paths simultaneously. Branches in an implicit
search will be called implicit branches.
To illustrate this, compare OTTER and
tableaux methods. In the new versions of OTTER both kinds of searches can be
implemented (the older versions accept only implicit search), while in tableaux
only explicit search can be followed. OTTER does not give explicit information
about the closed branches in an implicit search. That is different when
applying an explicit search. In this case OTTER provides a summary for a closed
branch at the moment the branch is closed and OTTER backtracks to explore
another branch. One of the main advantages of an implicit search when compared
with splitting is that it is easier to prune the search tree when similar paths
are found. On the other hand, one of its main disadvantages is that it needs
more memory as all paths are kept in memory simultaneously.
Nevertheless, a classification based on
these criteria is somewhat arbitrary, as almost any computational logic program
is a combination of syntactic, semantic, forward-, and backward-chaining
strategies. For illustration consider OTTER. It is predominantly syntactic, as
based on clause manipulation, and forward-chaining oriented, but it also
implements semantic ideas, such as the separation of clauses into two groups
(the sets of support and usable) and by the use of demodulators and
paramodulators (see above).
Bonacina’s classification (Bonacina, 1998
and 1999) is based on the third criterion above. She considers an implicit
branch search as clausal oriented, and a splitting one as goal oriented. The
two main categories in her classification are, on the one hand, those
theorem-provers with a ‘sub-goal reduction strategy ... if one considers the
single object they work on as the goal, each step consists in reducing the goal
to sub-goals’ (Bonacina, 1998, p. 257) (e.g., tableaux). On the other hand, she
considers those theorem-provers using strategies she calls ‘ordering-based
strategies’. She characterises these strategies as working ‘with a set of
objects [e.g., clauses], they use a well founded ordering to order the objects,
and possibly delete [e.g., using subsumption] objects that are greater than and
entailed by others’ (idem, p.
256). In this group is OTTER.
However, it is confusing to consider clausal
orientation as an implicit branch search and splitting as a goal-orientated
search. For example, as noted above, in the new versions of OTTER splitting has
been implemented even though OTTER is clausal oriented.
Bonacina’s depiction of the search process
seems similar to the description of a simulation. She illustrates the search
process as a chain of transition states, where a transition is generated by an
application of an inference rule. Each state is a step towards a desired final
state, where the proof is successful.
In the case of a logical model search using
tableaux, each state is a tableau. Given one state, a new state is generated by
the application of a transition rule over this tableau and the generation of a
new branch. The new state will be the tableau given by the addition of the new
branch to the old tableau. The desired final state is a closed tableau.
In case of a clausal search, a state is
given by the set of clauses in a search step. This set might consist in subsets
of clauses, for example, the sets ‘usable’ and ‘support’ in OTTER. Additional
subsets might be given by the implicit branching of the search. A transition
step consists in the application of an inference rule giving a new set of
clauses defining the new state. The proof is successful once a desired final
state is reached; that is, any subset of clauses representing a search path
contains a contradiction.
The criteria given in section 3.6.1 will be
used to add details about the search process in the theorem-provers SATCHMO and
OTTER, and to include in this classification logical model generation in a
simulation, namely an event-driven simulation, and the MAS-based simulation
scheme adopted in SDML.
1. SATCHMO.
This uses the sub-goal (backward-chaining) strategy of Prolog combined with a
logical model (semantic) search with splitting.
2. OTTER.
Originally OTTER was purely an assumption-based forward-chaining procedure
using clausal (syntactic) orientation with implicit path generation. New
versions of OTTER also allow the explicit use of splitting.
3. Event-driven
simulation. Usually simulation is forward-chaining and logical model-oriented.
It is rare to find simulation languages implementing splitting either
implicitly or explicitly. When experimenting with the dynamics of a simulation,
individual trials have to be generated by explicitly choosing the different
combinations of the factors for each trial. As it is a logical model search, it
can be interpreted as a tableau, but note that in a simulation not all facts
have to be deduced and some are left as unknown. Although it is similar to
tableaux (since it is logical model-oriented), it is different, as inference is
forward-chaining rather than backward-chaining. In theorem-provers like OTTER,
the order transition rules as given by certain clause weighting, while in
event-driven simulation this order is given by the future event list.
4. SDML.
Like most simulation languages, this is a forward-chaining logical model-oriented
language, but it enjoys facilities for splitting and backtracking and it is not
necessarily committed to generate all valid clauses in a logical model. State
transition rules follow an order given by the hierarchy of agents, the
hierarchy of time levels, and, finally, a partitioning of the space of rules
according to their dependencies.
The idea is to develop search and inference
procedures that allow a more flexible manipulation of the semantics than
traditional logic-programming and forward-chaining systems do. The call has
been for techniques that allow a semantic-driven search more adaptable to the
search process than unification (Frühwirth et
al., 1992).
A first answer came from logic-programming,
in the form of constraint logic-programming, commonly using Prolog, both as a
platform and as the programming style (Frühwirth et al., 1992). It is basically a backward-chaining inference
system. A second answer came from rule-based forward-chaining systems. Examples
are SATCHMO and CPUHR-tableaux calculus (Addennadher, 1995; idem, 1997; see also Frühwirth, 1994; Abdennadher
et al., 1999). Among the advantages
of these forward-chaining systems over constraint logic-programming are
introduction of user defined constraints and meta and higher-order reasoning
via rewriting of rules.
Constraint logic-programming can be
characterised by the interaction of the logic-programming inference engine and a constraint-solver
algorithm. constraint-solvers specialise in managing constraints in certain
domains (e.g., integers, booleans). The logic-programming engine calls the constraint-solver with a
set of constraints, getting as the answer a normalised solution for it and then
pruning the search space in accordance with this solution. A disadvantage
constraint-solvers face is that they are not open to the user, making difficult
their modification and application to new domains. Some rule-based
forward-chaining systems allow user manipulation of the constraint-solver.
There will exist both user-defined and built-in constraints. The first group of
constraints will be managed by rules the user gives, while the second one will
be managed by constraint-solvers. With illustrative purposes, in the next
paragraphs aspects of CHR will be considered in more detail.
‘CHRs define determinate conditional rewrite
systems that express how conjunctions of constraints propagate and simplify …
CHRs define simplification and propagation over user-defined
constraints. Simplification replaces constraints by simpler constraints …
Propagation adds new constraints which are logically redundant but might cause
useful further simplification’ (Frühwirth, 1994, pp. 90-91). In what follows a
CHR operational semantics will be considered to some extent in order to bring in
an idea about how it works.
In a CHR system, the inference engine is
characterised by the interaction of a logic-programming engine, a
constraint-solver (working on built-in constraints), and the rules working on
user-defined constraints.
Using Frühwirth’s notation, a state
in the search is given by the tuple of sets:
< GS, CU, CB>,
where GS is a the set of
goals, and CU and CB
are constraint stores for user-defined and built-in constraints. A constraint
store is a set of constraints.
An initial state might consist of
< GS,{},{}>, i.e., constraints are all embedded in the set of
clauses defining the problem and in the goal.
In case of logical model generation, a final
state in a branch of the search is given by < {}, CU, CB>,
if the search succeeds or by < GS, CU, {false}>, in case it fails (i.e.,
the branch is closed).
Consider how a state transition would
be. Suppose the state is:
< {C}U GS, CU, CB>:
that is, a subset of constraints {C} has appeared as a new goal during the
search process. Calling constraint-solver, if (C ʌ CB) is
logically equivalent to CB', in the next step it would produce: <
GS, CU, CB’>.
Similar modifications are generated by CHR
rules. In fact, CHRs will either generate simplifications in CU
while adding constraints to GS, or add constraints into CU
logically equivalent to some constraints in GS but leaving these
constraints’ store unchanged (constraints propagation) (Frühwirth, 1994).
Example 3-7
The sort of reasoning exposed above will be
illustrated by using a simplification of an example borrowed from Abdennadher et al. (1997).
Problem:
- John has enrolled in courses either
before 1994 or after 1995
- John was enrolled in cs30 before 1997.
In clausal form, it is expressed as:
enrolled(john, A,
B) ® (B < 1994) v
(B > = 1996)
(A,
C) = ({enrolled(john, cs30, T)}, { T
<= 1996})
Using notation for operative semantics given
above, this will be produce:
goal: enrolled(John, A, B), constraints:
(B < 1994) v (B > = 1996)
Applying logic-programming two sub-goals or
branches are found:
(A, {T <= 1996,
T <1994}) and (A, {T<= 1996, T >= 1996})
Then applying constraint-solver at each
branch, they are extended into:
(A,
{T <1994}) and (A, {T = 1996}), respectively.
For the second branch the final state is
achieved:
{enrolled(John,
cs30, 1996), {}).
In this example it is assumed there is only
one set of constraints to be solved by the constraint-solver. For more details
about CHR, see Frühwirth (1994)
and Abdennadher S (1999), or look at http://www.pst.informatik.uni-muenchen.de/~fruehwir/.
The sort of meta-reasoning certain reasoning
languages enjoy is quite convenient when proving tendencies. Examples of
languages that have explicit mechanisms for presenting meta-reasoning are
SATCHMO and SDML. SATCHMO allows the use of writing and eliminating of clauses
not only in the database, but also in the rulebase using ‘assert’ and ‘retract’
(Prolog’s built-in functions). Additionally, since it is written on top of
Prolog, SATCHMO itself can be easily modified. On the other hand, SDML enjoys
similar benefits from a meta-agent being allowed to read and to write rules in
other agents.
These supplementary facilities permit
reasoning about the inference system itself, e.g., writing rules depending on
how the search develops. An example would be: given only hints about a theorem
related to an overall tendency defined in terms of certain output, the theorem
might be elaborated by continuously updating an envelope for the output in
accordance to the simulation results. Also, after all logical models have been
found, relevant tendencies might be searched either over the whole space of
logical models or over a subspace of it.
In
this chapter the development of the ‘world view’ introduced in Chapter 2 will
be continued. The main aim of this is to set up a framework for a conception of
emergence of tendencies, which is a central notion in this thesis. A conception
of the emergence of tendencies seems to be strongly linked to a subject’s
knowledge and to an object’s complexity. A notion of the object-subject
dichotomy will be emphasised as a useful distinction once the subject’s bounded
rationality has been recognised.
The interest is not
only in tendencies observed in an empirical system but also in a simulation.
For instance, MAS-based simulation seems to be very helpful for understanding
some complex systems, for example, social systems. There, aspects of the
complexity of the ‘real system’, from the point of view of the scientific
community studying such a system, are recreated in the simulation. The
importance of observing and explaining tendencies in social simulation has been
pointed out for researchers in this community (see, for example, Edmonds et
al., 1998; Nigel, 1995; Conte et
al., 1997; Carley, 1998). The re-creation of properties of target complex
systems in the computer lab is what makes the simulation interesting in these
cases, as it is not possible either to implement this sort of experiment with
the target system or to get satisfactory knowledge of these tendencies via
models of a different nature (mathematical models or historical studies, for
example).
In applications
such as social simulation, where the number of agents is large and/or the
interrelations are subtle and hardly contingent to the dynamics of each
simulation trajectory, analysis of the design seems to be of limited use and a post hoc study becomes necessary. It is
common to find structural change or fluctuation in these systems, making their
analysis difficult (the simulation of systems undergoing structural change was
discussed in sections 2.5 and 2.9). Some of the difficulties involved in studying
structural change, and then complex systems, are: structural change develops
differently in different simulation trajectories, it is difficult to foresee how
it will unfold (e.g., what the new structure of the system will be after it
happens), and it is not easy to identify the factors triggering it.
The notion of
emergent tendencies will be seen in this thesis as relative to a modeller’s
difficulties in understanding an observed system, and linked to, on the one
hand, a modeller’s cognitive model and bounded rationality, and on the other
hand, by the observed system’s ‘objective complexity’. The discussion will
start by considering the usefulness of the distinction between subject
(observer) and object (observed phenomena) for understanding emergent
tendencies. Then, the central discussion in this chapter will be addressed.
First, a picture of a hierarchy of systems at different levels of phenomena in
accordance with their potential for complexity (which will be called objective
complexity) will be drawn. This is based on Heylighen’s ideas. Second, a
subjective notion of complexity in accordance with Edmonds’s conception will be
introduced. Third, using these two notions, a notion of what an emergent
tendency might be and what are its causes will be discussed. Finally, aspects
of a simulation related to emergent tendencies for a modeller observing a
simulation will be examined.
A basic notion in the view taken in
this thesis is the object-subject dichotomy. How this dichotomy is
understood and its relation to the idea of a subject’s bounded rationality will
be discussed. Bounded rationality is a central concept in social simulation –
it is understood as the existence of significant bounds in an agent’s cognitive
model for gathering information from their environment and for processing it
(Edmonds, 1999b). A pragmatic position will be taken for defining the emergence
of tendencies, a stance useful for the purposes of this thesis – in
particular, a position from which a subject’s understanding will be conceived
as conditioned by the interrelation between the subject’s language and the
observed object’s complexity. It is not claimed that this notion has general
philosophical or theological validity. Instead, it is based on the assumption
that the agents and subjects of interest have bounded rationality and on the
notion of object-subject dichotomy to be discussed below.
It seems that the less bounded is the rationality of an
agent with respect to relevant aspects of the environment (for its purposes),
the more deterministic the world (surroundings) will be for this agent. Here
‘relevant’ means those macro regularities that the agent perceives in its
environment that are useful for reasoning and taking decisions in terms of some
goals. Bounded rationality means that many aspects of the world will be
effectively indeterministic. Different agents with perfect rationality (assumed
deterministic in itself) and the same goals will share the same perfect
knowledge and will take the same decisions under similar ‘environmental’
conditions.
In general, the behaviour of a population of agents seems to
be non-deterministic, even if they have perfect rationality. This is because of
their differences in goals and experience (or the particular environmental
circumstances they have become involved into). If a group of agents with
perfect rationality collaborate to achieve a common goal and the environment
has no intention against them (e.g., there is no other kind of rational agent
in such an environment whose goals conflict with theirs), then the ‘resulting
world’ might be deterministic for these agents. Behaviour of one of these
agents will be predictable from another agent (or from a modeller) having the
same information. Examples of agents with perfect rationality include the agent
in a market as it is conceived in classical economics (Edmonds et al., 1998). These economic agents do
not necessarily have the same goals and collaborate. Economists use certain
‘game theory’ rules according to which, under certain conditions, behaviour of
their (classical economic) agents is predictable. Unless the opposite is
explicitly said, henceforth by ‘agent’ is meant agent with bounded rationality.
There seem to exist even more reasons for the behaviour of
agents with bounded rationality to be indeterministic. Bounded rationality
means that other aspects apart from goals and experience might make agents
behave differently. These differences are rooted in the limited information an
agent can capture from its environment and in the limited capabilities the
agent has to process the collected information. For each agent, there will be a
different ‘world view’. Different agents will behave differently under the same
circumstances. Agents with bounded rationality use different languages, though
the divergences might be only in the beliefs used as data to feed to their
‘inference procedure’. This might happen even if they have similar experiences
(it is assumed agents are able to learn from experience).
Each agent (a subject) has models of its surrounding
environment – almost certainly different from other agents’ models. As a
consequence, there is a subjective ‘world’ for each one. There will be shared
and unshared beliefs among agents. As more agents share a belief over time and
space, it can be said that this belief is less subjective. Similarities among
agents’ beliefs introduce the notion of knowledge with different degrees of
subjectivity. Indirect justifications of subjects’ knowledge such as
experimentation, theoretical developments, and modelling might influence
subjects’ beliefs. For example, it is possible for human beings to decrease the
degree of subjectivism of their knowledge by improving understanding of
phenomena via modelling (e.g., simulation) theory development and historical
discussion (see Figure
4.1). An increase in the degree of subjectivism of an
agent’s beliefs is understood in this thesis as an increase in the degree of
objectivism of these beliefs. Decrease in the degree of subjectivism of a
belief will hopefully bring that belief closer to the ‘real’ (hypothetical)
characteristic of the object the subject refers to with that belief.
|
|
Figure 4.1.Increasing objectivism in
subjects’ beliefs
|
In this discussion, it has been assumed implicitly that an
agent reasons about its internal model of the ‘world or surroundings’ rather
than about the world itself. On the one hand, there is a sort of subjective
world of the agent given by its mental models, goals, perceived phenomena,
beliefs, language, and every other ‘mental’ construct it has. On the other
hand, there is the ‘real world’ or empirical world – the source of phenomena;
i.e., there is a ‘real interaction’ subject-world, where the actions of this
and other subjects, on the one hand, and the new circumstances arising in the
world as the result of those actions, on the other hand, turn up as, in part,
the consequences of this subject’s actions; and there is a perception by this
subject of this interaction and of the consequences of its actions. Such a
pragmatic ‘division’ between a subject’s perception of the world, mental models
and language, and the empirical world itself is what in this thesis is called
the subject-object dichotomy. The notion of subject, then, is linked to this
mental model, language and perception, while that of object is linked to
phenomena where it is supposed the ‘real’ interaction subject-world takes
place. These cognitive agents (called subjects) will focus on those parts of
their surrounding with relevant behaviour for their intentions or goals, as it
is supposed to be useful for understanding phenomena, for modelling their
surroundings, and for taking better decisions. Hence, a subject-object
dichotomy, where the subject uses mental models to understand the object (which
is a system) has been identified.
In our later discussion about emergent
tendencies and complexity, this notion of an object-subject dichotomy will be
exploited and recognised as originating from both subjective and objective
factors. For example, a sort of trade-off between these subjective and
objective factors is associated with the likelihood that a subject finds
emergent tendencies in an object. It
will have an effect on a subject’s recognition of emergence and complexity
either in its environment or in a simulation. Then, in the following section,
the factors related to an objective view of complexity in an object, namely the
levels of complexity of systems, will be reviewed. Afterwards, a conception of
subjective complexity will be considered. Finally, the two notions of
complexity will be used to make up some conceptions of emergent tendencies
relevant for studying complex systems.
There are in the literature several
categorisations of systems in accordance with levels of complexity, as the
levels can be defined in many ways (see, e.g., Heylighen, 1997; 1991a; Simon,
1984). The main goal of this section is to present a relevant categorisation of
levels of systems, as this will be useful as a reference when settling notions
of objective complexity and emergence of tendencies.
The purpose of this classification is to elaborate the
fundamental distinction among systems in different levels of the hierarchy.
Thus, the higher the level of a system in the hierarchy, the higher the level
of control the system exhibits (following Heylighen, 1991a). The evolution of a
system from a lower level to a higher one is understood as the appearance of
variety at the higher level of control of the system, plus the rise of a new
control mechanism to select among these new options. This selector works as a
sort of constrainer over the new variety. A level subsumes a lower one in the
sense that systems in the higher level present the same characteristics and
properties that systems in the lower level have, plus some additional ones. The
higher the level of a system, the higher its potential for adaptation - it has
more options about actions and mechanisms to discern among these actions,
increasing the likelihood of taking good decisions. This new variety involves
new properties and adds unpredictability not present in the lower levels, as
well as an increase in the autonomy of the system. Unpredictability in a
system’s behaviour increases as there are more choices given by the increase in
variety. The higher autonomy and unpredictability introduces a new potential
for complexity (Heylighen, 1991a, 1995).
Heylighen (1991a) and Simon (1984) are particularly
interested in complexity of living organisms (systems with a vicarious
mechanism) and generally include in their descriptions only these kinds of
systems. They see such a hierarchy as the result of organisms’ ability to cope
with complexity in order to survive or to behave more satisfactorily. The first
level in the hierarchy is that of the simplest systems - inanimate systems. A
brief review of the complexity and the state of human knowledge at this level,
such as is seen in physics, is offered by Gell-Mann (1995; 1995/96).
An example of a hierarchy of systems is that given by
Heylighen (1991a). The more relevant characteristics of this description are
summarised in Table 4.1.
This table gives a hierarchy of phenomena for living
organisms. In the next sub-section, an alternative categorisation (including
inanimate matter) will be given. There, the intention is neither to dig much
into different levels of systems at each level, nor to have a level for each
level of control that has appeared in organisms during evolution (Heylighen,
1991a), but to capture their basic characteristics in relation to sources of
complexity and unpredictability in their behaviour – i.e., a useful
classification identifying the factors making difficult a subject’s
understanding of systems at each level.
Four levels of systems will be defined. In
the first one inanimate matter will be situated. In a second level all living
beings without reasoning will be placed, namely, those of biological systems,
including those at the level of ‘origin of life’ and those at the level of
‘learning’ in Heylighen’s hierarchy. Then, in a third level, organisms able to
reason (or self-aware organisms in more philosophical terms) such as ‘human
beings’ will be described. Finally, in a fourth level a meta-being, an
individual able to deal better than a common human being with the variety a
human being faces in a modern society, will be considered. This fourth level is
intended to provide a human being with a mechanism helping him to process the
huge amount of information he has to cope with daily in a dynamic modern
society and in dealing better with the choices he has in such an environment.
|
Level
|
Novel characteristic
|
|
Origin of life
(first pre-rational level)
|
Systems
at this level have a vicarious selector given by DNA.
‘The living cell is characterized by a self-producing (autopoietic)
organization, where the DNA controls the production of proteins and enzymes,
and the enzymes control the production of DNA’ (Maturana & Varela, 1980).
|
|
control of
position
(simple reflexes)
|
New
variety: movement. Selector-controller: control of position.
‘The movement will now be a function of particular features
of the environment sensed by the system. Sensory organs here act as media
translating features of the environment into an internal representation
(vicarious selector, see Campbell, 1974) which allows informed
decision-making.’
|
|
complex reflexes
|
Needed for controlling simplex reflexes.
Not discussed by
Heylighen.
|
|
Learning
|
Variety: mental model with non-deterministic decisions.
Control: Hebb rule.
‘The variety is here due to the fact that the synaptic
strengths, which determine the probability that a stimulus or excitation
would travel from one neuron to another one, are variable, so that the same
pattern of excitation may lead to different results. The variability of
synaptic connections accounts for what Turchin calls the capability to
associate, i.e., to create variable associations between representations.
Part of the control is realized through the Hebb rule, stating that a
synaptic connection that is used often will increase its strengths so that
the probability that it will be used later on increases… The Hebb rule makes
it possible for the system to learn by experience. … The associations that
are formed through learning are limited to phenomena experienced in spatial
or temporal contiguity’.
|
|
The rational level
|
Variety: concepts from a context can be used in other
contexts. Controller: experience (e.g., via social mechanisms).
‘The fact that the human can imagine a dog producing musical
sounds, while the rabbit cannot, signifies that the human has a larger
variety of possible actions. …concepts are separable from their context: they
retain (part of) their meaning when brought into contact with radically
different contexts. This can be understood by noticing that the concept can
be distinguished from the concepts it is associated with, and that this
distinction is stable or invariant: it does not change with the context
(Heylighen, 1990)…This means that we shall have to postulate a specific
mechanism that explains how any conceptual separation, however partial, is
possible…such independent external phenomena that can be associated with a
concept may be called symbols. A symbol is a stable, easily recognizable
phenomenon that can be combined with other symbols’.
|
|
Meta-beings
|
Variety: high quality information from the environment is
filtered and provided to a human. Controller: the named filter itself and
human rationality.
‘In the present view, the newly emerging control would be
situated on the level of the individual rather than on the level of society.
Each human individual would dispose of a metarepresentational framework,
implemented through an advanced man-machine interface, that would help him or
her in manipulating knowledge, in creating new concepts and theories, and in efficiently
gathering and organizing all the existing facts and values (s)he needs to
solve his/her problems. Practically, what was considered to be a privilege
that only a few persons of genius might achieve during their lifetime, namely
the creation of a completely new theory modelling important parts of reality,
would now become an automatic, everyday activity. This construction of a model would come as natural to
meta-humans as the formation of a sentence in verbal language comes to us’.
|
|
Table 4.1. A summary of part of Heylighen’s hierarchy
of systems’ complexity
|
This is the most basic level; here
are the simplest systems. Different instances of similar systems (e.g., planets
with similar physical constitution) under the same external conditions will
behave in exactly the same way. Behaviour of the system is basically determined
by external circumstances (environment).
Among the most
important cause-effect laws in this level there are: gravitation,
electromagnetism, and quantum mechanics. Note that these laws depend on the
environment or on the interrelation among different systems and objects. Their
effect cannot be changed arbitrarily by a particular system.
Uncertainty is pure in the sense that there
is no ‘intention’ in the entities involved in phenomena. Autonomy is null.
Complexity is due to randomness and basic laws such as those previously
mentioned.
Example 4.1
Matter in universe. Takes as an
example planets or components of an atom as understood in physics. Entities
show attraction and/or repulsion forces from where regularities such as
planets’ orbits around a central entity (a star) can be noticed by certain
subjects at the level of rational systems, for instance by humans.
The main science studying systems at this level is physics.
Objectivism (as understood in this thesis)
and even absolutism (here absolute knowledge is understood as knowledge about
reality theoretically perfect and complete) at this level seem to be reachable
via a theory of complex inanimate systems, which may be based upon quantum
field theory. One of the greatest defenders of absolutism has been Kant
(Solomon, 1996).
New particular phenomena: adaptation
and self-reproduction of systems.
At this level will be that subset of systems achieving the
level of the simplest subjects. i.e., those that have a vicarious mechanism but
are not aware of it (see Chapter 2). The simplest level of vicarious mechanisms
is found in the pre-rational level in Heylighen’s description. The higher level
in this hierarchy is given by those systems with a cognitive model but unable
to reason. In Heylighen’s view, at this level agents can learn but cannot
reason.
The mechanism for surviving, in the pre-rational level given
by Heylighen, is expressed in nature via the processes of reproduction,
variation, and selection of individuals in a population of systems by using,
for example, DNA. Entities in a generation reproduce and yield descendants for
a next generation. Via some selection mechanism only the ‘well adapted’ will
participate in this reproduction. Randomness is present in the variation
process (mutation). Generally, there is adaptation of the species over its
evolution to new circumstances by passing on features that allow well-adapted
behaviour from generation to generation. Characteristics of those well adapted
are transferred to their descendants. Useful information about both system
structure and behaviour is passed via genes. This gives, in part, the
additional variety a system at this level has with respect to a system at the
previous level. The new level of control (internal variation-selection) is
based on a system’s genes.
The new control (new respect to the lower level of systems
described above) of a system at this level consists of the mechanism used to
actuate appropriate information content in the genes for ‘good behaviour’ in
the particular circumstances the system faces, and to pass useful information
to descendants (DNA). The activation mechanism involves basically an organism’s
enzymes. New unpredictability in behaviour of the system appears, as there are
no deterministic decisions about which information in the genes will be actuated
and which will be passed to descendants. Systems have more choices at this
level, as there is an internal vicarious mechanism where by a selection about
behaviour is made. In this sense, as there is a new variety and an internal
selector, the system has won certain autonomy.
This level of systems includes not only pre-rational
organisms, discussed until this point, but also organisms able to learn.
However, learning at this level is somewhat primitive; this corresponds to
Heylighen’s learning level. At the learning level given by Heylighen, selection
of models in the mental level of a system is not in control of the system
itself but of laws such as ‘Hebb rule’. From the system’s ‘point of view’, this
is a sort of blind learning. A system’s decision in a particular situation
might depend on its ‘feelings’ about a similar situation it had found before
and the evaluation of the consequences of its actions in that past situation in
accordance with its goals. Very primitive feelings such as fear or confidence,
which are associated with pain or satisfaction, can be recognized in some
systems at this level, for example in animals. In simulation, this sort of
unconscious learning can be modelled by weighting of rules of behaviour
(Edmonds et al., 1998).
Example
4.2
Typical example: living organisms like animals or
organisations made up of these entities (e.g., colonies of ants). Another
example might be a population of evolving computational agents representing
those agents at this level observed in reality.
Main science: biology. Computational models using MAS have
been widely used for helping biologists.
This level might be redefined using other sources of
knowledge than biology, modelling, and applications in computer science. For
example, for some philosophers, the additional source of complexity at this
level would be what Arthur Schopenhauer called will (Solomon, 1996). At this
level some philosophers include the notion of ‘hidden unconscious wills’. Among
these wills Solomon mentions the ‘will to live’ and the ‘will of love’.
New phenomena at this level: a
systems’ self-awareness and ‘rational’ control over its actions. The subject’s
vicarious mechanism becomes more complex; a control at the cognitive (mental)
level appears. The new phenomenon at this level is described as a certain
degree of freedom at the rational level by computer scientists and modellers
(e.g., as defined by Heylighen; see a summary of his view in Table 4.1), and, as free will by many philosophers (Salomon,
1996). This idea of freedom at the mental level means a certain ability ‘to
play’ with mental constructs some systems at the previous level already have,
e.g., concepts and beliefs in Heylighen’s view, but for which these systems in
a previous level do not have variety.
Some philosophers consider that phenomena at this level,
such as a human’s intentions and goals, have a more abstract and subtle origin.
They suggest that ‘free will’, is the final source of phenomena at this level.
Several definitions of free will going from strong notions, which are of
interest in, e.g., philosophy and theology, to weak notions, which are of
interest in, e.g., computer science and modelling, might be displayed.
Philosophical views of free will seem to bring philosophers into endless
discussions, which are not of interest in this thesis. Likewise, notions of
free will in theological terms might be explained in very ‘soft terms’, e.g.,
as linked to ‘virtues’ some of ‘god’ or divinity (e.g., someone in a higher
level than human beings) give humans. In a less strong way, such notions might
be linked to emotions and other human virtues and probably related to some
conceptions of autonomy. For instance, they can be seen as linked to very
‘special capabilities’ of a human such as initiative and the ability to change
his goals. Finally, weaker notions of ‘free will’ than those previously
considered could be seen as associated to special abilities in an agent’s reasoning.
For example, Edmonds (2000) has presented some guidelines
for modelling a weak notion of ‘free will’. He describes a notion of free will
in these terms: ‘It means that an agent is free to choose according to its
will, that is to say that sometimes it is its deliberations on how to achieve
its goals that determine its actions and not just its circumstances (including
past circumstances)’ (idem, p.
2). This conception is close to the notion of reasoning given by Heylighen (see
the summary of his description of systems at the rational level in Table 4.1). Nevertheless, it seems that Edmonds recognises a
certain additional independence in the agent’s reasoning in terms of some
‘creativity’, e.g., when writing, ‘The process of deliberation leading to a
choice of action has to be free in the sense that it is not constrained to a
particular ‘script’ - this means that there is also some choice in that
deliberation, as well as choice in how to make that choice, and choice in how
to make the choice in how to make that choice etc.’ (idem). In this thesis, there is more
interest in notions like Heylighen’s idea of reasoning and Edmonds’s
suggestions for modelling a ‘weak’ conception of free will than in the strong
philosophical and theological ideas of free will. This is so because these
softer conceptions can be useful in simulation – indeed similar ideas have
already been used for modelling computational agents (e.g., see Edmonds,
1999b).
Both Heylighen and Edmonds recognise that at this level of
complexity the behaviour of an individual (a system) does not depend only on
the circumstances, but also on internal reasoning and on a weak notion of
self-awareness as the system might also have a simple model of itself. It is here
where the notion of the subject-object dichotomy is useful, since the system
becomes a subject able to reason and to make choices regarding aspects of his
behaviour. Here that dichotomy can be noticed as given by, on the one hand, the
reality when the subject interacts with his surroundings, and, on the other
hand, his perceptions of that reality as they are captured by the agent’s
language.
As was stated above, the new variety at this level appears
in a subject’s cognitive model – the subject is able to play with mental
constructs. The new and higher control in the system appears as a capacity for
subject-driven rationality. At this level, its capacity to keep models of the
environment appears along with its ability to anticipate possible consequences of
its own behaviour, behaviour of the environment, and behaviour of other
subjects. There is a certain mental flexibility granted by, to some degree, a
context-independent reasoning (as in imagination). However, such independence
is not complete (as with the imagination) but rather controlled to a certain
extent by the context and that subject’s reasoning and values. For example,
humans in modern society are in part controlled by social norms, work norms,
common sense, religion, and media. These also bring into a subject’s cognitive
model new ideas, further associations, and reasoning.
All this gives a higher level of autonomy to a system than
at level 2 and introduces more unpredictability - it is not easy for an
observer (e.g., another subject or a modeller) to foresee either the
alternative actions the system will consider or the final choice the system
will make.
Individuals (systems) at levels 2 and 3 can group and
interact into communities and societies. The dynamics of these interactions are
even more difficult to understand than that of the components. Examples are
communities of humans where organisations and institutions appear as a result
of cooperation and competence among groups (Carley et al., 1998). The complexity of social systems made up of individuals
at this third level is tremendously high, as are the institutions and
organisations these individuals create. The dynamics of these systems allow
tendencies to appear which are difficult to understand by the interacting
agents and by a modeller of these systems. Studying human systems is the
concern of people working in social simulation. Existing methodologies for
studying these systems are not totally satisfactory (see Chapter 2, and especially section 2.10). Among the aims of this thesis is to provide a
methodology for studying the emergence of tendencies, especially those causing
social complexity (see Chapters 5 and 6).
The sciences studying systems at this level include:
economics, sociology (including social simulation), soft systems, and
psychology. There is a great deal of argument in human research concerning systems
at this level.
As in Heylighen’s view (see Table 4.1), in this section a meta-human is seen as a social
human who is better able to cope with the difficulties faced by a social human
seeking to achieve ‘good’ behaviour in a modern society. These difficulties are
fundamentally due to a subject’s bounded rationality and to the large amount
and variety of information this individual finds in a social system. In the
next paragraphs, the origin of such difficulties will first be discussed.
Usually, mechanisms in a ‘meta level’ are proposed for helping a human being to
cope better with such complexity.
In general, difficulties in a human understanding of
phenomena are explained as due to their bounded rationality (as pointed out by
Simon, 1982). Heylighen sees the problem precisely in the subjectivity of
humans’ knowledge. He identifies as the main weakness in a human’s knowledge
the limitations of his conceptual codes:
‘each conceptual code will be impaired by its (not admitted)
subjectivity, by its limited number of concepts, and by its tendency to reduce
holistic phenomena to combinations of discrete elements.’ In his opinion, a
move towards objectivism in a social agent’s mental beliefs is convenient. He
points out that this has already been a tendency in the historical accumulation
of knowledge in philosophy, religion and science.
Heylighen associates increase in variety in society in the
last century with cultural revolutions such as relativity and quantum theory,
and with the massive use of communication and transportation media. In his
view, these two factors, plus some changes in values, have brought a release of
social and cultural constraints. Massive access to media by people has allowed
a faster spread of, for example, knowledge, ideas, technology and fashions. The
mental associations each individual makes increase the variety even more.
He proposes a technological framework for helping a human
control this variety and for decreasing the level of subjectivity in humans’
knowledge. Such a device would be especially useful for ‘storing, transmitting
and processing information’ (see Table
4.1). The idea is to increase a human’s rational
capabilities indirectly by using computational devices able to capture and
process information, and then abstract and filter it in conformity with an
individual’s goal. Mechanisms for helping in this direction at the present time
include: MAS, database interfaces, and information systems (as conceived in
computer science and management).
Here a notion of complexity from the
other side of the coin of the object-subject dichotomy, i.e., a subjective
notion, will be presented. In this view, knowledge is basically relative to a
subject’s language. For example, what is obvious, simple, complex or emergent
will depend on its judgement.
Edmonds (1999a) discusses a
conception of complexity observing that different notions of complexity can be
found in the literature. He points out many misinterpretations of the term and
argues that complexity must be differentiated from other notions of difficulty
such as size, number, ignorance, variety, randomness, expressivity,
irreducibility, dimension, and order. He gives the following definition of
complexity:
‘Complexity
is that property of a model which makes it difficult to formulate its overall
behaviour in a given language, even when given reasonably complete information
about its atomic components and their inter-relations.’
This definition is closely linked to the
notion of a subject’s bounded rationality and identifies a subject’s language
(and hence its subjectivist character) as the final cause of complexity.
As in the case of the discussion
about complexity, emergence can be seen either from an objective or subjective
point of view. Referring to the discussion in the two previous sections, first
an objectivistic notion of emergence, based on an objective notion of a
systems’ complexity, will be given. Afterwards, a subjectivist version of
emergence of tendencies linked to a subject’s bounded rationality will be
presented. Finally, a notion of emergence of tendencies, supported by a
trade-off between the named subjective and objective factors on which each of
the previous definitions rest, will be offered.
In the previous section, it was
pointed out that the higher the level of complexity of a system, the higher its
autonomy, the unpredictability of its behaviour, and the potential of the
system to present regularities that are difficult to understand by an observer
(subject). Hence, the higher the level of complexity of a system, the higher
the likelihood that such a system presents emergent tendencies to that subject.
Less important factors for an objectivist view of emergence
of tendencies in a system than its level of complexity can be identified. The most significant of these seems to be
the nature of the changes the system is undergoing. A system experiencing only
quantitative change is supposed to be easier to understand than a system
suffering qualitative or structural change. An example of structural change
occurs when a new controller appears in a system, bringing it from one level of
complexity to a higher one (as was discussed in section 4.3 above). A case of this sort of change is the rise of the
European Union (here a new geographical-political entity appears), along with
which a controller, represented by the Council of Ministers, the European
Commission, and the European Parliament, arises.
An additional factor of objective complexity and emergence
seems to be the degree of coupling of a system’s components, that is, the
extent of the dependency of properties of the whole on properties of the
components. Consider, for example, how the life of an animal depends on
different parts of its body. This property (life) is more dependent on certain
of the animal’s components and on properties of those components than on other
components and their properties; e.g., it is more reliant on the animal’s heart
or blood system than on its hair or on its extremities.
This degree of dependency or coupling seems associated with
the reversibility of properties of both the whole and the components with
respect to disaggregation and aggregation of components. There are properties
of the whole that are very intricately linked to the structure of the system.
If, for example, components are disaggregated, the system loses that property
and, in many cases, the property cannot be restored by aggregating the
components. An example is life in an animal (the whole). An animal will loses
its life if its heart is separated from its body. Furthermore, life cannot be
returned by bringing the heart back to its original position. To keep the
property ‘life’ of the whole is possible, in some cases, only in very special
conditions, e.g., in a scientific laboratory, where each separated component is
kept under similar conditions to those undergone by it before being separated
from the whole. Likewise, a component might irreversibly lose properties when
separated from the whole. For example, a heart separated from the body embarks
on a decomposition process that changes its properties. This immediate change
in the properties of a component, started as soon as the component is separated
from the whole, seems also to be associated with the irreversibility in the
properties of the whole. Similarly with the case of the whole, in some cases
properties a component undergoes before being separated from the whole could be
kept during a limited period of time if the component were held under special
conditions. Notice that in the case of the named property of the whole, i.e.,
life, it can only be kept if the component (the rest of the body without the
heart) is restrained to special conditions, but once the property is lost it
cannot be restored again.
In this paragraph the level of complexity a system (object)
is embedded in has been identified as the main factor for the emergence of
tendencies in an objectivistic view. Other important factors in this view seem
to be the nature of the changes that system is undergoing (qualitative or
quantitative) and the degree of coupling of its components.
In this section, emergence will be
characterised as purely relative to a subject’s cognitive model. The general
idea is that a subject will consider a certain tendency perceived in a system
as emergent if, having information on a system’s components, the subject finds
it difficult to explain that tendency (following Edmonds’s definition of
complexity, 1999a). This notion of difficulty leaves open the possibility for a
range of definitions of emergent tendency. The stronger ones will be defined in
terms of a subject’s language and will be closer to Edmonds’s definition of
complexity as well as to a conception of emergence presented in Edmund et al. (1999). These notions will be
linked to a strong idea of explanation of a tendency: a tendency is explainable
in the ‘theory’ content in a subject’s language if it is deducible from that
theory. On the other hand, the weaker notions of emergence of tendencies will
be founded on a softer notion of explanation of a tendency, one based on a
conception of satisfiability of the subject with a certain explanation of such
tendency. This notion may be more appropriate for modelling some systems, e.g.,
a social system.
As an example of a strong notion, consider a subject, S,
using languages L1 and L2 to reason about phenomena perceived in an object, O,
defined as a system at a certain level of complexity. It will be said that a
certain tendency observed by S in O is emergent when
descriptions
given in the language (L2) the subject uses to express overall patterns in the
object are not reducible to descriptions in the language (L1) the subject uses
to describe the design of the system (see Figure
4.2).
Using this stance, the notion of a potential
for emergence of tendencies can also be described in the following manner:
the higher the level of complexity of the
perceived system and the more bounded the subject’s language, the higher the
potential for emergence of tendencies in the subject-object interrelationship.
For a weaker notion of emergence of tendencies, a
notion of satisfaction will be applied as the criteria an agent uses for
evaluating its own performance and satisfaction of its goals, following Simon’s
ideas (Simon, 1982). Replacing the notion of reduction among languages (used
above) by a notion of satisfiability, a tendency observed by a particular
subject in a particular system would be considered emergent if
descriptions
given in the language (L2) a subject uses to express overall tendencies in an
object (a system) are not satisfactorily explained by descriptions in the
language (L1) the subject uses to describe the design of the system.
An even weaker definition of emergent
tendency is as follows:
a
tendency observed by a subject in a system would be considered as emergent if
the subject does not have a satisfactory explanation for that tendency.
|
|
|
Figure 4.2. Emergence of tendencies for a
subject observing a system
|
A tendency is no longer considered as emergent for a subject
as soon as the subject finds a satisfactory explanation for it. A satisfactory
explanation might appear either as a result of changes in the subject’s
explanation of the tendency, i.e., as a result of the subject’s reasoning,
through the gathering of more information related to that tendency and the
updating of the subject’s mental models, or, because the subject’s notion of
satisfiability is relaxed, e.g., owing to changes in the subject’s goals. In
none of these cases must the subject’s language necessarily be altered.
In the case of the first two definitions (those using the
notion of languages), the tendency loses its characterisation as emergent if,
e.g., a new language L3, able to fill the gap, appears in the subject’s
mental model (see Figure
4.3). Additionally, the former languages, L1 and L2,
might be, in some sense, subsumed by the new language, L3; i.e.,
knowledge expressible in L1 U L2 is also representable in L3.
Example 4.3
1. In
this example the strongest notion of emergence of tendencies given above will
be used. Consider the languages for describing movement of bodies in space,
e.g., movement of planets in the solar system, allowed by Einstein’s relativity
law. This language had the role of the new language L3 appearing for
satisfactorily explaining regularities not understood using the languages
available to the scientific paradigms existing in physics at the time it was
conceived. One of these regularities was the particular elliptical pattern a
planet describes in its revolution about the sun. Language L1 was that
language given by the old paradigm, i.e., Newton’s gravitational law, now
replaced by L3. L2 is the language used to describe
mathematically that elliptical orbit a planet describes. This description might
come first from observations of the planet in its movement about the sun; e.g.,
they might be a sequence of spatial positions the planet has occupied. A
mathematical model of this pattern of movement (a tendency) can be built using,
e.g., numerical methods for interpolating those points. How good this model is
can be checked by comparing predictions of the model with new measurements.
This model, described in a hypothetical language L2, is not well
explained by using a language L1 allowed by Newton’s gravitational law.
Nevertheless, it will be well explained by a model of the relation space-time
in a language L3 enabled by Einstein’s general theory of relativity.
Tendencies like this are emergent for a subject using language L1
but not for a subject using language L3.
|
|
Figure 4.3. A new language L3 is used by the subject
and the emergent tendency is no longer considered emergent
|
2.
Consider a certain geometric area, e.g., a circle, and the
points it is made of. Suppose that a language L1 is used to describe
points and its properties and another language L2 is used to describe
the area and its properties (e.g., size of the area). Assume also that this
language L1 is ‘poor’ in the sense that it does not include mathematical
notions such as differential and integral calculus. It might be impossible to
explain the size of the area of the circle using language L1, and then this
property (size) will be considered emergent. After ‘discovering’ the
differential and integral calculus (language L3) properties of a
geometric area, such as its size, can be explained satisfactorily in terms of
properties of the points in this area and the language L3.
In this example,
a property of the whole (area) is explained by properties of the entities
(points) in terms of which it is defined
by using a mathematical model of the relation between the property of
the whole and properties of the components. This model is given in the language
L3. It seems common to find cases of emergent properties where the gap
among descriptions has this sort of source: the whole and the components are of
a different nature (mathematically). This different nature is sometimes
expressible as a different dimension between the elements constituting the
whole and the whole itself. Similar examples can be brought from applications
of integrals, series, and other mathematical ‘tools’.
3. An
example where the source of difficulty for explaining a regularity has
similarities to that shown in the previous example but where that regularity is
not expressible mathematically will be examined. Consider an agent answering to
the question: ‘what makes a picture more than its separated lines?’ (this
example has been borrowed from Edmund et
al. (1999)). For recognising a picture, a subject captures certain patterns
of the outline of the picture and compares them with its ‘mental’ prototype
(his model) of what is a picture. Assume the subject has a language L1
used for describing lines (potential parts of a picture) and a language L2
used to describe general regularities observed in the whole figure. It would be
difficult for a subject to explain why that particular figure is recognised as
a picture using L2, as this language only permits descriptions in terms
of lines. Many regularities perceived as pictures for a subject using L1 will
be emergent. Assume now that the subject has a new language L3, allowing
him to capture and explain more patterns in the picture, e.g., other patterns in addition to
lines, than if using language L1. Patterns are sub-models the subject
uses to define a figure. He may, for example, define the picture ‘face’ as that
consisting of the following patterns: a whole closed area (having a certain
shape and representing the borders of the face), a short line perhaps slightly
curved (representing a mouth), a point (representing the nose), and another two
points (representing the eyes); and the constraints given the relative
positions among these sub-models. A definition of a figure might be part of the
definition of a wider figure, so that, for example, the definition of the
figure ‘face’ might be used for defining the figure ‘human’. Such patterns seem
to be more helpful for explaining what a figure is than those offered by the
language L1. Then, a subject’s prototypes of figures are more flexible,
as they include a wider variety of forms. In this case, the subject’s new
language, L3, can be used to express basic patterns useful to describe a
figure as well as individual lines and the figure itself. It can be used to
explain patterns, including lines, captured in the figure, and a picture in
terms of those patterns and their interrelations. More likely, this new
language rather than language L1, would allow an agent to find a
satisfactory explanation for the question posed above.
The work developed in this section
has produced a compromising notion of emergence, taking into account both the
objectivist and the subjectivist views. The emergence of tendencies will be
recognised as dependent on both objective and subjective causes. The conclusion
is that, given a subject-object relationship, where the subject is a system at
the third level of complexity or above and the object is a system at any level
of complexity, the higher the level of complexity of the system and the more
bounded the cognitive model of the subject, the higher will be the likelihood
that the subject finds emergent tendencies in the object.
A weak (subjective) notion is chosen as the more appropriate
to describe emergence for a modeller observing a simulation. A tendency
observed by a modeller in a simulation would be emergent if:
descriptions
given in the language (L2) the modeller uses to express overall tendencies in
the simulation are not satisfactorily explained by descriptions in the language
(L1) that the subject uses to express the design of the simulation.
This chapter is aimed at offering an
alternative methodology for exploring simulation trajectories, a methodology
allowing one to implement stronger notions of morphism than those commonly
found in the literature and associated with the notion of approximation
discussed in 2.6.
This methodology is also intended to help a
modeller (a subject) to understand aspects of interest in a simulation better
(and, by extension, in a target system). A modeller (for instance, a computer
scientist, a biologist, or a manager) usually seeks to behave ‘well’ either in
an area of research related to the target system or in the target system
itself. In the first case, his aim is to understand the target system better,
while, in the second case, he is also interested in being well informed as an
agent acting in such a system. For instance, a manager is usually interested in
understanding his business environment better where he is an ‘active’ agent,
while a biologist is commonly interested in studying biological systems where
he is not usually an agent. Hence, the methodology to be proposed is intended
to have both informative and ‘instructive’ orientations.
The need to better understand a certain kind
of tendencies in the dynamics of a target system is what motivates a simulation
in many areas of research. In areas such as social simulation, it is of
particular interest to analyse processes and to better understand tendencies in
social behaviour (Carley et al.,
1998). In management and policy analysis, simulation is valuable to guide and
inform managers and policy analysts, assisting them in taking decisions (Wack,
1985a and 1985b; Domingo et al.,
1996). Information allowing more general conclusions will help in all these
areas of research to test theories and hypothesise about the simulation and the
target system, and will assist managers and policy analysts more convincingly.
It is of particular interest for such
modellers to analyse the commonality of emergent tendencies in different
simulation trajectories, as this allows them to draw conclusions about the
theory implied in the simulation. However, there is usually a trade-off between
the richness of the study in terms of the number of explored trajectories
(sometimes related to how fine-grained the simulation model is) and the amount
of required computational resources. The finer the simulation model, the
more ‘realistic’ the simulation model
will be, but also the more intricate the analysis of the simulation will be.
A typical case where this analysis is
crucial is in the MAS-based simulation of social systems. There, modellers
attempt to generate certain ‘complex’ tendencies in the dynamics of a whole
population and in the behaviour of an agent as the result of the interaction of
individuals (agents), where unforeseen behaviour of individuals and
unpredictable tendencies in the behaviour of the whole population can arise
(Edmonds, 1999).
A factor that limits the comprehension of
emergent tendencies is the lack of alternative methodologies and tools for
appropriate exploration and analysis of the dynamics of a simulation. As
explained in section 2.6, present methods include examining individual
trajectories, as in scenario analysis (Domingo
et al., 1996), and statistical
sampling, as in Monte Carlo techniques (Zeigler, 1996). In both cases, the
scope of conclusions is limited. Also, they have some drawbacks for modelling
complex systems (see section 2.10).
This chapter is aimed at developing an
alternative way of exploring and analysing a MAS-based simulation by systematically
and automatically enveloping all possible trajectories in a substantial
fragment of a simulation theory as a complement to existing methods. More
specifically, this thesis proposes a complete search of trajectories for a
range of parameterisations and agents’ choices. This kind of search corresponds
to a logical model exploration in theorem-proving (see section 3.5.2). Conclusions will be more general than when using
the named alternative methods. In addition, the proposal will be made to
analyse tendencies in a simulation by enveloping them for the subset of
explored trajectories. An envelope places emphasis on the results from the
worst investigated cases rather than on average measures.
The exposition in this chapter is as
follows. First, in section 5.2, non-deterministic factors in, and driven by,
the dynamics of a simulation will be pointed out. Basic aspects of the proposed
methodology, namely a constraint-based exploration and envelope of a subspace
of simulation trajectories, are discussed in section 5.3. In section 5.4 generalities about the sort of exploration of post hoc analysis to be proposed in this
chapter are given. Afterwards, in section 5.5, more fundamental theoretical
aspects with respect to the kind of exploration (namely, a logical model
envelope of simulation trajectories) and the sort of proof intended (necessity)
are elucidated. In section 5.6, the relationship between proving the necessity
of a tendency in a simulation, on the one hand, and a modeller’s satisfactory
explanation and understanding of the tendency, on the other, are addressed.
This discussion is useful for figuring out the usefulness of proving tendencies
for understanding better emergent tendencies in a simulation. Section 5.7
depicts the sources of constraints on the proposed constraint search. Both
technical ones, related to computational modelling, and other, more pragmatic
ones, associated with difficulties in modelling complex systems, are taken into
account. Generalities about the proposed methodology for translating a
MAS-based model into a constraint-based model for proving tendencies is covered
in section 5.8. Section 5.9 examines in detail how such a translation process
can be implemented in the simulation language SDML (there the relevant aspects
of SDML for achieving this sort of proof of tendencies are listed). Finally,
section 5.10 discusses the aspects of this translation that
suggest it is isomorphic.
Factors for experimentation in a
simulation will be linked to causes of variety in a system’s states. Factors
defining variety at the structural level of a system will be called parameters.
Each alternative parameterisation will define a different structure of the
system. Variety at the dynamic structure means alternatives for the system’s
behaviour or branch points in the simulation trajectories. They stand for the
options (non-deterministic behaviour) the processes the system undergoes can
follow. These factors will be called choices.
Experimenting with a MAS-based simulation consists in
generating different trajectories or alternatives for the behaviour of a system
via changes of either parameters of the model or choices of the processes the
system undergoes. Different parameters and choices will be linked to
non-determinism. This non-determinism was seen in the description of the
hierarchy of levels of complexity of systems (see section 4.3) as grounded in the autonomy and unpredictability of
the system. There, factors conveying this unpredictability were also pointed
out. Usually, in this research, choices will be represented by the alternative
actions available to agents. Each choice becomes a branch point in the
simulation, with each alternative in the choice representing a different
simulation trajectory.
Another factor present in a simulation is the underlying
logic of the simulation language.
This thesis proposes to analyse the dynamics of a simulation
via enveloping outputs, the analysis of emergent tendencies being of particular
interest for the work presented here. This represents an alternative to
traditional methods such as those based on central measures (e.g., Monte Carlo
studies).
Merriam-Webster’s dictionary at http://www.m-w.com
defines ‘envelope’ in the following terms:
Main Entry: envelope
Pronunciation: 'en-v&-’lOp,
÷'än-
Function: noun
Date: circa 1714
1 : a flat usually paper
container (as for a letter)
2 : something that envelops :
WRAPPER <the envelope of air around the earth>
3 a : the outer covering of an
aerostat b : the bag containing the gas in a balloon or airship
4 : a natural enclosing covering
(as a membrane, shell, or integument)
5 a : a curve tangent to each of
a family of curves b : a surface tangent to each of a family of surfaces
6 : a
set of performance limits (as of an aircraft) that may not be safely exceeded;
also : the set of operating parameters that exists within these limits
In 1, 2, 3, and 4, is presented the most common usage found in everyday
life. There an envelope is conceived as a container or covering, consisting,
e.g., of hard material (e.g., a cover of a letter) or of a softer one (e.g.,
the air around the earth); but no constraint is posited about its nature. There
are three elements: a physical one clearly perceived, that enveloped; and a second
physical one, the cover or container; and finally, a relation among these two:
the enveloping relation.
In 5:, the
idea is better formalised. There the mathematical notion is offered. In
mathematics an envelope is conceived as a curve/surface tangent to a family of
curves/surfaces. Now some constraints are added to the concept. First, both
entities, the enveloped and the enveloping, are mathematically defined objects:
a curve/surface, and a family of curves/surfaces, respectively; and second, the
enveloping object must be tangent to the enveloped one.
Finally, 6
introduces a new notion about the concept; what is being enveloped is neither a
physical object nor any mathematical function, but the behaviour or performance
of something (let us assume that this something is a system). This performance
can be characterised directly by observing the outputs of the system, or
indirectly by placing constraints over some parameters that are supposed
appropriately to anticipate such behaviour. This second method does not seem
convenient for analysing the dynamics of a simulation, as the dynamics of a
simulation is difficult to understand from the design (that is why a post hoc study of the simulation outputs
is of interest in this thesis). However, it is of interest in this thesis to
define in advance that space of the theory where the dynamics of the simulation
will be explored, and this is achieved by placing constraints over the
parameters of the model and over the choices of the processes. A typical study
of the relation between these simulation outputs and factors of the simulation,
i.e., parameters of the model and choices of the processes, is data analysis,
though its methods (e.g., principal components, factor analysis) are based on statistical results. It would
be of interest to explore the use of envelope following methods like those of
data analysis.
But, how could we envelope the
simulation outputs?
The simulation outputs are functions over time represented
by a set of values (one for each time instant considered). Using Zeigler’s
notation (see section 2.3) the collection of values for a variable is called Y,
and its representation over time is refered to as r.
Should several outputs be considered, say n of them, the collected set
of outputs will be called Y1, Y2, …Yn
and their representations over time r1, r2,
…rn.
It is important to remember that the intention is to make
the output comprehensible for a modeller. Consequently, it does not seem
convenient to use the strong concept managed in mathematics. Rather, an
envelope will be chosen considering the trade-off between practical usefulness
for a modeller and precision (by precision we mean how close it is to the ideal
mathematical notion of a tangent curve/surface).
Enveloping one-dimensional outputs
First, consider the case of enveloping a single output Y.
Each trajectory will generate a sequence of real values over time, Y.
Calling yij the output value at time instant i for
trajectory j, an envelope might consist of two sequences of values over
time: Eupper and Elower , which in some
sense cover all trajectories. The value of Eupper at time
instant i must be greater than or equal to yij for all
j, and Elower at time instant i must be lower
than or equal to yij for all j. That is,
the envelope would be given by two sequences of values over time, where for
each time instant all values generated by the simulation trajectories are
enclosed by the two values given by these two value sets. Putting this in other
words, at each time instant, t, the smallests interval covering all
points generated by the explored trajectories is included in the interval given
by the two sequences Eupper and Elower for
instant t. This tactic is exemplified in the case presented in Chapter
7.
Alternatively, first an approximating function, f,
for the value set Y that each trajectory generates of the output might
be elaborated; then, the instances of these functions (one for each trajectory)
might be enveloped in accordance with the mathematical definition or a related
one (i.e., a tangent curve or other function enclosing all instances of f might
be developed).
Enveloping multi-dimensional outputs
Until this point, the enveloping of each output
independently of any other has been considered. However, this does not always
have to be the case. We might also be interested in the interrelation among the
outputs, in which case that we would have to consider all outputs as a
multi-dimensional function over time. Assume that a value set Yh
is generated for each output. After generating all trajectories, there will be
a collection of values (Yh)ij representing each
value for output h at time iteration i for trajectory j.
This data could be arranged in different manners. For example, each trajectory
can be seen as generating a matrix of values where each column would have the
collection of values for a time instant, and each row the collection of values
over time for each output variable (for trajectory j, the datum at the
position hi, Yhij, would represent the
value for the output h at iteration i).
Assume that two output variables are of
interest. Considering them over time, there would be a three-dimensional
collection of points. As for the one-dimensional case, the envelope could be
discrete, when it is defined over the discrete outputs the simulation
generates; or continuous, if an approximating surface for that
three-dimensional collection of points is generated and then enveloped.
In general, either a discrete or a continuous enveloping
surface for the multi-dimensional function hypothetically defined by the
outputs of interest might be generated, taking into account the trade-off
between precision and the modeller’s goals.
Final remarks
Among the procedures of interest for enveloping tendencies
in simulation studies might be the following:
o
Enveloping certain properties of the observed
tendency rather than the tendency itself. In this case, it is supposed that
a certain mapping from the tendency gives the output of interest (the
properties to be enveloped). It may be of interest for a modeller to prove that
certain properties of a tendency are within certain bounds. This may be
achieved by showing that their envelope satisfies certain conditions. It would
allow a modeller to affirm that the tendency satisfies certain properties in
accordance with the simulation model theory – defined by the envelope of the
properties of the tendency achieved via a simulation. The results might permit
one to relate the simulation results to theory developments and to elaborate
conclusions with respect to the theory underlying the simulation model.
o
Producing a mathematical description of some
coarse borders of the space where the tendencies have been observed. This is
useful if it is difficult to describe the subspace of the tendencies directly.
Then, coarse borders are chosen as a first approximation to the envelope and,
afterwards, these enclosing borders are expressed mathematically.
o
Using extreme cases of representative or typical
instances of a tendency. In this such cases it is assumed that the observed
tendencies in the simulation can be grouped qualitatively as similar or close
enough (in accordance with some
criteria) to a finite number of typical tendencies.
o
Specifying a range of parameters and choices.
This is the original description of the subspace of explored trajectories used
in the previous paragraphs (it is also similar to definition 6 in
Merriam-Webster’s dictionary presented at the beggining of this section).
A simulation - either an event-driven, a finite
differences, or a MAS-based - can be seen as a partial logical model generation
(see section 3.5.2). Usually, in a trajectory only a partial set of all
the facts of the logical model corresponding to the trajectory are produced.
This partial set consists of those facts that are relevant, either because they
are required for the modeller as outputs or because they are necessary to
generate the simulation transition steps. The remaining ones are left as
unknown (see Chapter 3).
There are different methods to specify a theory in a
language. One commonly used in logic is via a set of formulas of the language
that become the axioms of the theory (see section 3.2.1). In a declarative program a simulation model is
specified via a set of rules and the underlying logic of the program. Potential
trajectories are defined via non-deterministic factors of the simulation, e.g.,
parameters and choices.
In this chapter we propose analysing the emergence of
tendencies in a simulation by exploring a subspace of the space of
trajectories. This will be done via a (logical) model-based constraint search,
where the constraints will stand for the selected parameters and choices. It
will allow a modeller to explore that fragment of the simulation theory content
over a range of parameters and choices (see Figure
5.1). Consequently, the resulting conclusions and proofs
will be valid over that fragment of the theory and, under appropriate
justifications, they can be extrapolated to the whole simulation theory.
|
|
Figure 5.1. Theory given by simulation trajectories
|
Like scenario analysis, the idea is to generate individual
trajectories for different parameterisations and agents’ choices, but, unlike
scenario analysis, the exploration is constrained to only a certain range of
parameters and choices.
Akin to Monte Carlo techniques, it explores many possible
trajectories, but, unlike Monte Carlo studies, it explores an entire subspace
of trajectories (rather than some randomly generated sample of the whole) and
is able to give definitive answers for inquiries related to the dynamics of the
simulation in that subspace.
The idea is to generalise about tendencies going from
the observation of individual trajectories to observation of a group of
trajectories generated for certain parameters and choices. In particular it is
intended to know if a certain tendency is necessary or contingent in the
explored trajectories. We understand a simulation trajectory (or, shortly, a
trajectory) as a logical model embedded in a simulation program (a ‘possible
world’ in semantic terms) and involving trajectories of entities (e.g., agents)
inside the simulation and, hence, different from trajectories of these
entities. It is a cross-product of all settings of the structure of the simulation
model and all processes (e.g., agents’ choices) into one path through a
high-dimensional space (see Figure
5.2).
The character of the search will be predominantly (logical)
model constraint, forward-chaining, and clausal ordered. A logical model will
be generated for each combination of parameters and choices. Each combination
of parameters provides a different structure of the simulation model (see Figure 5.3). ‘Paths’ representing trajectories are generated for
each structure. Then, while the simulation is going on, choices produce branch
points where alternative settings for each choice turn out into a different
simulation trajectory. The order of the inference will be given by rule
dependencies. Possible origins of rule dependencies will be explained below.
|
|
Figure 5.2. Representation of a simulation theory in terms of
the simulation trajectories, and of these in terms of agents’ choices (for a
single parameter-setting and assuming there are two agents)
|
This exhaustive constraint-based search over
a range of possible trajectories makes it possible to establish the necessity
of postulated emergent tendencies. Following a procedure similar to that used
in theorem-proving (see Chapter 3), a subset of the possible simulation
parameterisations and agent choices is specified, the target emergent
tendencies are specified in the form of negative constraints, and an automatic
search over the possible trajectories is performed.
Thus, a subset of the possible simulation parameterisations
and agent choices is specified, the target emergent tendencies are specified in
the form of negative constraints, and an automatic search over the possible
trajectories is performed.
Tendencies
are shown to be necessary, with respect to the range of parameterisations and
non-deterministic choices, by first finding a possible trajectory without the
negative constraint to show the rules are consistent and then showing that all
possible trajectories violate the negation of the hypothetical tendency when
this is added as a further constraint. This is equivalent to showing that all
possible tendencies obey the positive form of the constraint, i.e., that the
positive form is true for all tendencies.
|
|
|
Figure 5.3. A model constraint-based exploration of the
dynamics of a simulation
|
For instance suppose there are two cities - a first city, called
the‘origin city’, City-O, and a second one, called the ‘target city’, City-T
- and that, after some natural phenomenon (e.g., a heavy fall of rain), the
routes communicating between these two cities have become badly affected (it is
assumed there are several possible routes). As a result of the natural
phenomenon, many, or possibly all, of the routes between the two cities have
become blocked. Assume that there is a subject in City-O who believes
all routes have been blocked and wishes to prove that this hypothesis is true.
One way to implement the proof is to assume that the route is not blocked
(e.g., to assume as true the negation of the hypothesis) and then send ‘an
explorer’ to investigate each possible route (to follow a possible route will
be equivalent to the exploration of a simulation trajectory). If the
investigated route is found to be blocked, then there will be a contradiction.
The contradiction results because, on the one hand, the negation of the
hypothesis (i.e., ¬ (‘all routes are blocked’)) was assumed to be true (the
negation of the hypothesis for a particular route would be ¬(the route is
blocked’)), and, on the other hand, the hypothesis has been proved to be true
for the investigated route (the hypothesis for a route is ‘the route is
blocked’). Once the contradiction occurs in a route, the ‘explorer’ goes back
(this is equivalent to a backtrack in the simulation) to the most immediate
branch point in the investigated route in order to attempt to reach City-T
by following an alternative route, e.g., by chosing another branch at that
branch point. If the ‘explorer’ finds a contradiction in all possible routes,
e.g., all possible paths are found bo be blocked, then the hypothesis has been
proved to be necessary.
Another example is the case study to be presented in Chapter
7. The exploration of a route in the previous example corresponds to a
simulation trajectory there. However a simulation trajectory is more complex as
it is a cross-product of all parameter- and choice-settings, as was noted in
the previous section. The task of the explorer when following a route is
simple: to check if that route is blocked. The task of the simulator generating
a trajectory is more complex: to generate a logical model, that possible
logical model (or possible world) associated with that parameter- and
choice-settings. There would be a large amount of detail that might, or might
not, be useful for a modeller. In the case to be given in Chapter 7, choices
appear in a trader’s price-imitating – for this purpose, a trader chooses
another trader for comparing prices and sales. In a simulation trajectory,
there will be three agents’ trajectories with choices (there are three traders)
and another three agents’ trajectories without choices (there are three distributors).
The number of possible simulation trajectories in this case is huge. An
exploration of the trajectories would be useful, on the one hand, to prove a
tendency, and, on the other hand, to inform about detail in a trajectory.
However, there would usually be a trade-off between the richness of the study
in terms of detail explored in single trajectories (sometimes related to how
fine-grained the simulation model is) and the power and the number of
trajectories explored – also associated with the limited computational
resources. To explore a single trajectory in detail would help to explain why
agents have made particular decisions and then, probably, to understand a
tendency better, while an exploration involving more trajectories would help in
proving it, i.e., in making conclusions more general.
The proof-based approach to be proposed in
this chapter ihs similar to tableaux and different from OTTER in that it is logical model-oriented (see
Capter 3). It is similar to OTTER and different from tableaux because it is clausal ordered, but it uses
an order criterion different from OTTER’s. It is similar to tableaux and a version of OTTER with splitting, as it
searches each branch, explicitly backtracking once a contradiction happens
(i.e., when the negative constraint is violated).
John Casti (Casti, 1992) considers the concept of
explanation and compares it with the concept of description. For
him, an explanation answers to the question ‘why?’, while a description
answers to the question ‘what is?’. For instance, if a subject perceives
a light, a description of the light might involve an account of its intensity,
brightness, and colour; while an explanation might specify some of the reasons
for the light’s being perceived as it is, so that it might answer the question
why it ‘has’ that specific colour, brightness, and intensity that the subject
observes.
For Casti, ‘an explanation involves giving an
account of an already known fact on the bases of logical conclusions drawn from
well-established general theories’ (Casti, 1992, p. 387). He recognizes a
hierarchical structure of perceived facts, where what is explained is at a
higher level than the components of the explanation.
He affirms that giving a causal description for a process
and providing a formal explanation of it are synonymous. From his position, the
concept of description is wider than the concept of explanation.
The term ‘to explain’ is defined in Merriam-Webster’s (http://www.m-w.com/home.htm) as:
1
a: to make known b: to make plain or understandable <footnotes that explain
the terms>
2:
to give the reason for or cause of
3: to show the
logical development or relationships of
Thus, we see that an explanation is a sort of description,
but a description where reasons supposed to be better known than what they try
to explain, either more intuitively or based on other reasons, are given. Here,
an important notion is stressed: that an explanation gives meaning to
the explained phenomena. This meaning is supposed to be offered with respect to
a cognitive model or to a logical theory.
Accordingly, an explanation usually comes as a justification
in terms of known facts, which in turn are justified in terms of other facts,
and so on. Ultimatelly, all facts are justified in terms of some ‘primary’
facts usually called ‘principles’ or axioms.
Consequently, an explanation of a tendency in a simulation
should come in terms of the simulation principles or axioms, e.g., in terms of
the simulation design. Ultimately, it should be given in terms of the design
language. On the other hand, an explanation in a subject’s cognitive model
would be given in terms of elements of its language – facts at the pre-lowest
level would be justified in terms of his more basic beliefs or intuitions.
Let us now turn to the concept of
understanding. To understand is to know. There is implicit the idea of a
subject as the know-er - as that agent who realises and finds the meaning of
some phenomenon in terms of its internal language. There seems to exist a
strong link between the notions of explanation and understanding. However, not
all explanations of a phenomenon can be considered as part of a subject’s
understanding, but only those causal descriptions offering meaning to the
observed phenomenon in terms of elements of a subject’s cognitive model. On the
other hand, not any understanding comes from an explanation. For instance,
something could be understood using those principles in the lowest level of
understanding - what in a subject’s cognitive model would be the subject’s
intuitions and facts.
The Oxford Advanced Learner’s Dictionary offers the
following definition for the term ‘to understand’:
1(a):
to know the meaning of words, a language, a person’s character, etc.
(b): to perceive the meaning or importance
of something, to perceive the explanation for or cause of something.
2
to have a sympathetic idea of awareness of somebody/something
3
(a) to be aware from information received that
(b) to assume that something is the case;
to take something for granted
4
to supply or insert an omitted word or phrase mentally
In this definition, again, understanding is
closely related to a subject’s given meaning to something via its cognitive
model. Once more, meaning could be based on either an explanation (e.g.,
definition 2(b)), or on intuitions and faith (e.g., definition 3(b)).
Summing up, in this thesis an explanation
will be understood as a causal description offering the subject reasons and
probably also givin sense and meaning to certain phenomena perceived in an
object (in terms of using components from a theory or from a subject’s
beliefs). On the other hand, understanding will be conceived as the meaning the
subject has for something in terms of its cognitive model. This meaning might
come from an explanation (corresponding with a theorem when it is an
explanation based on a logical model) or from an intuition (corresponding with
an axiom in a logical model).
Finally, let us review the notion of proof and proving. The
Merriam-Webster’s dictionary defines ‘to prove’ as:
1 archaic: to learn or find out by experience
2 a: to test the truth, validity, or genuineness of <the
exception proves the rule> <prove a will at probate> b: to test the
worth or quality of; specifically: to compare against a standard -- sometimes
used with up or out c: to check the correctness of (as an arithmetic result)
3 a: to establish the existence, truth, or validity of (as by
evidence or logic) <prove a theorem> <the charges were never proved in
court> b: to demonstrate as having a particular quality or worth <the
vaccine has been proven effective after years of tests> <proved herself a
great actress>
4:
to show (oneself) to be worthy or capable <eager to prove myself in the new
job>
Alternatively, the Oxfords Advanced Learner’s Dictionary
says:
1 To show that
something is true or certain by means of facts or evidence.
As is seen, the idea of proving is related to notions such
as genuineness, trueness, and accurateness. Refereing again to our previus
example of observing a light, it might be of interest to prove that the light
has the quality an observer affirms he perceives, e.g., a certain degree of
brightness, or specifications of colour. A proof has similarities with an
explanation, as they both consists of some sorts of causal descriptions, but is
different in that it is a causal description that pretends to show trueness and
intends to be more objective as it is based on specific theories and methods
(e.g., a logical theory) rather than on any theory or on a modeller’s cognitive
model.
Procedures can be used to implement a proof in accordance
with what has to be proved (the nature of the phenomenon) and by the means we
have for elaborating the proof (e.g., a computer, a mathematical model, a
physical laboratory). In this thesis, it is of interest to prove a theorem
defined as a tendency in the dynamics of a simulation in terms of the theory
content in the simulation model. In this case, proof procedures are derived
from logical theories.
The idea would be to show that, under the
theoretical content in a simulation model a certain fact is true. That is, it would consist in showing that
the theorem is a fact in the simulation model theory. This might be ahieved via
an appropriately justified (as a proof) causal description.
A subject might take a proof procedure as an
explanation if the subject can explain the tendency giving similar reasons to
those involved in the proof. In this case, the subject is supposed to
understand the proof procedure, in the sense that the subject is able to
elaborate an explanation similar to the proof procedure and based on his
cognitive model. It is important to remark that, in general, a proof procedure
is only a means for achieving a proof. The important point is simply to show
that the theorem is true (the proof) rather than the proof procedure itself.
A more precise definition of the notion of proof to be
managed in this thesis is given in Chapter 3 (see particularly section 3.2).
There a proof is defined as a computational procedure for verifying the
validity or inconsistency of a formula or theorem with respect to a theory.
In the light of the previous discussion and also of
Chapter 3, proving the necessity of a tendency in a simulation informs a
modeller that the tendency is a fact in the simulation theory by showing that
it appears in all possible simulation trajectories or logical models of
simulation model theory; i.e., the tendency is a fact in the theory content in
the simulation model (see section 5.5).
On the other hand, a subject understands a tendency if it
can give meaning to the tendency, that is, if it finds an explanation or an
intuition in his cognitive model giving sense to the occurrence in the
simulation.
A computational proof of a tendency might, or might not,
help the modeller to understand that tendency. A proof procedure works upon
facts on a computational model, while giving meaning to a tendency observed in
the simulation on which a modeller’s understanding is based works upon facts in
the subject’s cognitive model.
Proving and understanding can correspond to different
modeller’s goals and, in general is achieved via different strategies. For
example, for a modeller aiming better to understand a tendency, it might be
enough to explore a single simulation trajectory. In this case proving the
tendency would waste computational resources by needlessly exploring the whole
range of trajectories and might provide too much information to help improve
the modeller’s understanding. Also, the level of detail and the how the
information is offered to a modeller plays a role here, as it will be easier for
a modeller to find an explanation for a tendency if the simulation offers
outputs which the subject can relate to knowledge he already has in his
cognitive model (e.g., those coming from his observations from and experience
with the empirical system).
Part of the structure and the interaction of these
two systems are presented in Figure 5.4. The modeller’s given cognitive model is in
accordance with the discussion of section 8.6, where ideas from Salomon’s (1996) interpretation of
aspects of Kant’s philosophy are presented. Other features of this figure come
from the previous discussion about explanation, proofs, and understanding and
from the discussion presented in Chapter 4 about emergence of tendencies.
Since emergence of tendencies and the complexity of a
system are based on both the objective complexity of the object and the bounded
rationality of the subject, the difficulties for computational modelling of a
complex system can be understood as having a subjective source (the subject in
this case would be the computer, and its mental model would be given by the
simulation program): the limited computational resources; and an objective
basis: the objective complexity of the simulation model and the nature of the
modelled changes (changes in the simulation model might, for example, be
qualitative or quantitative; state transitions could be defined in terms of
numerical or symbolic manipulation). These difficulties could also be
understood as constraints for simulating a complex system. More specifically,
we characterise the possible origins of constraints in simulations of complex
systems as beloning to one of two groups:
·
Those sourced in the limitations of a modelling
device. In this thesis the modelling device is a computer. Here are the
‘subjective’ constraints, which, in this case, are technical constraints.
o
Limited computational
resources
o Manipulation of real numbers: making
it difficult to evaluate the similarity between paths (i.e., between different
simulation trajectories) and to prune the search.
·
Those sourced in the complexity of a simulation
model, and probably ultimately rooted in the nature of the changes a
modeller perceives the target system is undergoing.
o
Nature of the modelled change. It is especially
difficult to model a system undergoing structural change (see sections 2.9 and 4.3).
In order to make possible a
theorem-proving procedure about the theorems in the theory of a MAS-based model
(see section 5.9), we will attempt to carry out a homomorphic
translation (see Chapter 2) from the original MAS into a platform where the
alternative trajectories can be unfolded more efficiently. The MAS will be
translated along with the range of parameterisations and agents’ choices. The
platform it is translated into is described in the next section. Each
trajectory in the new platform will correspond to a possible trajectory in the
original MAS. This transformation seems to be a particular case of isomorphism,
the two systems being equivalent in many respects (see section 5.10.1). The
equivalence between the two systems is based on a stronger notion of morphism
than the weak specification commonly used in simulation, which is based on the
idea of approximation (see Chapter 2). Specifically we translate the original
MAS-based model into a simulation model with a single database-rulebase pair
(see Figure 5.5).
The translation is useful because it allows
the computationally efficient exploration of trajectories, and the achieving of
restricted proofs of theorems in a MAS-based model. This translation is
practical for dealing with several difficulties for modelling in MAS. Among
these difficulties we have, first, the limitation in computational resources and
the complexity of the task (usually too many trajectories have to be
investigated), and, second, the technical hitches in experimenting using a
particular MAS model directly, since data and rules are encapsulated in
different abstractions and hierarchies like those of agents and time levels.
This encapsulation makes it difficult and sometimes even impractical to
experiment directly with simulation models of complex systems in a MAS.
|
|
Figure
5.5. Transformation of a MAS
into a single database-rulebase pair
|
This methodology is useful for enabling
proofs to be made. Nevertheless, the proof procedure is usually inefficient
because aspects of the structure of the rulebases and databases inherited from
the MAS inhibit efficient proof, and so further efforts to achieve efficiency
might be needed. For such a purpose it might be convenient to take advantage of
dependencies between rules. The translation process might already have been
useful for revealing rule dependencies. Afterwards, unhidden dependencies can
be unwrapped and then exploited to make the modelling exploration process more
efficient.
In this section it will be shown how to achieve the
translation specified in the previous section, using the simulation language
SDML.
SDML is not only suitable for the purposes of this
thesis, as it is a declarative language for programming MAS-based simulation
models, but also because it offers facilities for (logical) model
constraint-based search (Moss et al.,
1997). Among the advantages it shares with declarative programs, there are the
following:
·
Modularity. Any part of the simulation model is
constructed as a group of standardised units (i.e., rules) allowing flexibility
and variety in use. The declarative paradigm facilitates a greater level of
modularity than the imperative paradigm because the control of the program is
separated from the content. This flexibility is useful both when representing
the static structure of the system and when generating the dynamics of the
simulation. It facilitates the introduction of alternatives for agents’ choices
and parameters of the simulation model.
·
Expressiveness. Effective conveyance of meaning
is a consequence of the representation of the system as linguistic clauses on a
set of databases. It facilitates the
interpretation of a set of social phenomena into a simulation by allowing the
dual interpretation of clauses as pseudo-linguistic tokens and as entities to
be computationally manipulated.
·
Easier analysis. Context-situated analysis of
detailed data, and tracks of trajectories, as well as analysis of groups of
trajectories, is much more straightforward than in imperative programs because
the resulting databases can be flexibly browsed and queried.
·
The Possibility of Formal Proof. The data
generated by the dynamics of the simulation can be analysed as a logical
extension under the particular logic of the simulation language. It opens the
possibility of achieving proofs related to the logic of the language and the
constraints imposed by the allowed choices of the agents and parameters of the
simulation model.
Among the particular advantages SDML offers for implementing
a forward-chaining, (logical) model, semantic-driven search that is clausal
ordered, and explicitly split, are the following:
·
Good underlying logical properties of the
system. The core of SDML’s underlying logic is the Strongly Grounded
Autoepistemic Logic (SGAL) described by Kurt Konolige (1995).
·
Its backtracking mechanism facilitates the
exploration of alternative trajectories via the splitting of simulation paths
according to the agent’s choices and the simulation model’s parameters.
·
The efficient forward-chaining assumptions
manager in SDML tracks the use of assumptions. Assumptions result from
non-deterministic rules.
·
A collection of useful primitives relevant to social
simulation is available.
·
A meta-agent
for automatic translation of rules.
A meta-agent (meta, for the purposes of this presentation) is an agent
‘attached’ to another agent as a controller; it is able to write rules for that
agent. This is used here not as an agent per se but as a module
used to ‘compile’ rules into an efficient form as well as to monitor and
control the overall search process and goals.
·
A mechanism for an automatic and static analysis of
rule dependencies.
·
Simple
negative contradiction generation via a false predicate: P => ⊥.
·
User defined backward-chaining clauses
useful as demodulators.
This sub-section is intended to
clarify how SDML’s inference mechanism works, in order to help in better
understanding the translation procedure of the MAS-based model into a (logical)
model constraint-based architecture.
The SDML inference mechanism is
forward-chaining (though it allows backward-chaining rules used to implement
auxiliary manipulations needed by other rules - these rules can be conceived as
the demodulators that are found in OTTER; see Chapter 3). A simulation is
usually implemented in SDML in a way such that the antecedent retrieves
instances of data valid for the past simulation time in order to generate data
for the present simulation time (and perhaps the future):
antecedents
of the rules instantiate existing facts in the database =>
new facts are added into the
database in accordance with the consequents of the rules whose
antecedents have successfully matched facts in the database.
The exposition will be guided by examples. They will be used
to describe key points such as: what happens when a rule fires, why a rule
dependency is created, how SDML knows when a dependency should be (or might be)
placed between two rules. Also, the usefulness of the assumption mechanism and
of using a meta-agent will be addressed.
The idea is progressively to introduce features of SDML’s
inference mechanism. In this sense, a latter example will display aspects of
this mechanism not exposed in a former example. For facilitating the
discussion, we will first depict informally an algorithm very similar to that
used in SDML. This allows one to show the main characteristics of SDML’s
algorithm. Additional features will be shown progressively by the examples. The
exposition to be followed will allow us, on the one hand, to show drawbacks of
this first algorithm, and, on the other hand, to introduce additional features
of SDML’s algorithm (as changes made in this first algorithm in order to add
efficiency). Among the aspects to be considered later are ‘backtracking’ and
‘rule dependencies’.
First informal approximation to SDML’s algorithm
Introducing the forward-chaining mechanism and the
idea of tagging assumptions to facts in the database,
(a) For each rule, it is checked whether the antecedent
holds;
(b) For a rule whose antecedent holds, all bindings (e.g.,
all sets of values for its variables that match the database) are found;
(c) For a rule whose antecedent holds, the consequent with
respect to each of these bindings is asserted to the database;
(d) If it is possible that the antecedent will be later
contradicted by the action of another rule,
‘tags’ are added to the relevant facts in the database in the form of an
assumption; and
(e) Once all rules have fired as often as they can, the
assumptions are checked for consistency. If no contradiction exists, the
simulation of that rulebase successfully finishes.
1st Example.
Assume the following two rules have been written in SDML:
R1: True => P(a); P(b);
R2: P(?x) ^ P(?y) => Q(?x,
?y);
where:
- P, Q and True
are predicate names (True permits a rule to fire unconditionally, i.e.,
it is used to place facts in the database);
- a and b
are constants;
- and ?x
and ?y are variables
Initially the database is empty, so by step
(a) only the first rule fires - its antecedent always holds. According to (b)
and (c), the database will contain:
Database: P(a); P(b)
As there is no rule with a consequent that can contradict
the antecedent of the rule that has fired, e.g., the predicate True, no
contradiction is possible. Step (d) does not find it necessary to ‘tag’ the
generated data with an assumption.
Step (e) finds that the database has been updated and there
is new data that can make R2 fire, so that the simulation cannot be stopped.
The steps of the algorithm are followed again from the beginning (there is no
need for this rule to check assumptions as there are none).
According to (a), SDML checks again the antecedent of the
rules using information from the updated database. Rule R1 does not give
new information. Now the antecedent of rule R2 holds. Then, by steps (b)
and (c), and after the corresponding unifications, the database becomes:
Database: P(a); P(b); Q(a,b);
Q(a,a); Q(b,b)
For a second time, there does not exist any rule whose
consequent (action) could contradict the antecedent of the rule that has fired
(R2), so no assumption is necessary.
Step (e) finds that there it is no possibility of generating
new information - all rules have fired as often as they can. In addition, there
is no need for checking consistency of assumptions, as there are none. In
consequence, the simulation is finished.
2nd Example.
Introducing the dependencies mechanism
Assume the rulebase consists of the rules:
R1:
True => P(a) ^ P(b);
R2: True => R(c) ^ R(d);
R3: P(?x) ^ R(?y) => Q(?x,
?y);
Following the algorithm given above, we check the rulebase.
The two first fire and the database becomes:
P(a); P(b); R(c); R(d);
In a second application of the algorithm, the system finds
that only R3 gives new information and the database grows to:
P(a); P(b); R(c); R(d);
Q(a, c); Q(a, d); Q(b, c); Q(b,
d);
Then the simulation stops as ‘all rules have fired as often
as they can’ and there is no data with a linked assumption tag.
Notice that for each trial of the algorithm, all rules have
been checked out and only some of them have fired. There were two applications
of the algorithm. In both of them the three rules were checked, but not all of
them fired: an the first attempt only R1 and R2 fired and at the
second attempt only R3 fired. Because of these failed attempts, the
procedure is inefficient.
A more efficient algorithm will be that where rules are
checked in some order according to some dependencies between the antecedent of
one rule and the consequent of another rule. In this example, data generated in
the consequents of R1 and R2 are used in the antecedent of R3.
It is convenient to consider firing rule R3 only after rules R1
and R2. Dependencies exist between these rules and can be explicitly flagged
(see Figure 5.6). In general, dependencies are detected between a
pair of rules if the consequent of one of them is instantiated by the
antecedent of the other one.
After dependencies are added, the algorithm given above can be
slightly modified and made more efficient. Now, steps (a)-(d) are applied to
each rule in the database following the order of the dependencies, and then,
after all rules have been checked in accordance with that order, step (e)
inspects the consistency of the assumptions and the end of the simulation.
This new procedure is more efficient than the previous one.
It can be better explained below when applying it to an example. First, any of
the rules R1 and R2 can be checked, as their antecedents do not
depend on other rules’ consequents. After steps (a)-(d) have been applied to R1
and to R2, the database becomes:
P(a) ^ P(b); P(c) ^ P(d)
Only then is R3 inspected, e.g., steps ((a)-(d)) are
applied to R3 (this is in accordance with the order given by the dependencies
shown in Figure 5.6). This rule fires and the database becomes:
P(a); P(b); P(c); P(d);
Q(a, c); Q(a, d); Q(b, c); Q(b,
d);
|
|
Figure 5.6. Rulebase dependencies for the 2nd
example
|
As we reach the end of the dependencies graph (and all rules
have been checked), then step (e) is carried out, and, in conformity with this
step, the simulation is finished. Following the new algorithm, each rule is
inspected for only once (and the simulation finishes after following the
algorithm only one application of the algorithm), while in the previous
algorithm each rule needed to be inspected several times – and in this sense
rule dependencies add efficiency into the inference engine.
3rd Example. Showing
how the assumptions mechanism works and its usefulness
In this case, in order to make the explanation clearer, we
will consider three cases.
Case 1: Showing how the predicate
‘not inferred’ (¬) can be used
Assume the following two rules were written in SDML:
R1: True => P(a) ^ P(b);
R2: P(?x) ^ P(?y) ^ ¬(?x = ?y)
=> Q(?x, ?y);
where the symbol ¬ means not
inferred. The proposition not inferred (?x = ?y) can be taken as
conditionally true if (?x = ?y) is not inferred from the database.
Should the rule fire under that supposition, an assumption ‘tag’ will be added
to the data placed into the database. SDML tags a datum with an assumption when
it can change in the future, as is the case when the predicate not inferred (¬)
is used. Another way for generating assumptions (in addition to the use of the
predicate ¬) is when the antecedent of a rule can be contradicted by the
consequent of another rule.
The main stages in the simulation of this example would
be (in this case the algorithm will not be explicitly referenced (as
above), but its basic steps are followed):
1.- SDML’s inference engine
partitions the space of rules and builds the rulebase (see Figure 5.7). In the example, the consequent of rule R1 is
referenced in the antecedent of rule R2 (by P(a) and by P(b)). Then a
dependency is placed between these rules.
2.- After creating the rulebase with
the (static) rule dependencies, the simulation
|
|
Figure 5.7. Rulebase dependencies for the 3r
example (Case 1)
|
begins. Rules are checked for firing
in accordance to the generated dependencies and rulebase partitioning. First,
the rule R1: True => P(a) ^ P(b) is considered. As it fires,
the rulebase will consist of:
P(a); P(b)
3.- After firing R1 and
updating the database, the inference engine passes on to check the rule R2:
P(?x) ^ P(?y) ^ ¬(?x = ?y) => Q(?x, ?y). The first part of the rule
fires as the predicates P(a) and P(b) are already in the
database. In addition, as the constants a and b can be assumed
different (there is no information in the database contradicting this), the
remaining part of the antecedent of R2, e.g., ¬(?x = ?y), can be taken as true under
this assumption. Then the rulebase and assumption set (which until this
point was empty) are updated (see Figure
5.8).
|
|
Figure 5.8. Database for the 3r example (Case 1)
|
4.- As ‘all rules have fired as
often as they can’ and the assumptions
are consistent, the simulation stops. If there were a rule generating data
contradicting the assumption made in the previous step, then the associated
data (e.g., Q(a,b)) would be discarded. In such a case, the simulation
would backtrack to the point where the rule generating the assumption (R2) was
fired, and the simulation would be restarted from that point on.
Case 2: showing how the ‘no
inference’ mechanism can be used to generate different logical models for the
rulebase
Consider the rules:
R1: ¬Rainy => Sunny
R2: ¬Sunny => Rainy
The graph of dependencies is given
in Figure 5.9. This set of rules (R1 and R2) forms a
(logical) ‘partition’ as there is a cycle in the dependencies. The
antecedent of a rule placed late in the dependencies graph (R2 in this
case) depends on the consequent of a rule preceding it in that graph. This
cycle defines a sort of iteration when firing the rules. It is not only rule R1
that can generates data yielding new firings of rule R2, but the reverse
can also happens.
|
|
Figure 5.9. Rulebase dependencies for the 3r
example (Case 2)
|
Assume R1 is considered first by the inference
mechanism; then the data:
Sunny under the assumption:
¬Rainy
would be generated. However, if R2
is considered first, the database would consist of:
Rainy under the assumption
¬Sunny
We would say that there are two possible (or allowed) worlds
(logical models) for this rulebase, as there is no additional
information for conceding one of them and discarding the other. Some inference
mechanisms would accept one of these logical models (using some criterion)
while others would accept both of them. SDML’s inference mechanism would
arbitrarily choose between the two rules and then would accept that logical
model generated by the chosen rule. However, should a contradiction arise in
the explored logical model, SDML would attempt to find and alternative logical
model by backtracking to the point where the assumption was generated and
making another choice (in this case there would be only one left). This is the
sort of mechanism that we will use in the example to be given in Chapter 7 for
investigating all traders’ choices for price-imitating. These aspects of SDML’s
inference mechanism are better explained below in Case 3.
Case 3: Showing
how SDML’s backtracking mechanism works
Assume, the rulebase consists of:
R1: ¬Rainy => Sunny
R2: ¬Sunny => Rainy
R3: Sunny => ^
where the symbol ^ stands
for contradiction (or, for false).
The dependencies graph is shown in Figure 5.10. According to this graph, rules R1 and R2 fire
before rule R3. Assume R1 is chosen first, then the database will
consists of:
Sunny under the assumption:
¬Rainy
This allows R3 to fire and generate the
contradiction: ^.
This contradiction will be found by step (e) of the algorithm given above.
There (in that algorithm), it was not specified what the program has to do if a
contradiction is found. To include this possibility, the step can be rewritten
(it will allow the algorithm to consider backtracking when a contradiction is
found, as is the case in SDML):
(e)
Once all rules have fired as often as they can, the assumptions are checked for
consistency. Should no contradiction exist, the simulation successfully
finishes;
otherwise, the system backtracks to the point where
the assumption generating the contradiction was generated and attempts another
alternative at that simulation branch point (then another simulation trajectory
is set off).
|
|
Figure 5.10. Rulebase dependencies for the 3r
example (Case 3)
|
In consequence, as a contradiction appears, the system
backtracks. The alternative the system finds is to fire R2. Then the
database will become:
Rainy under the assumption
¬Sunny
In this case the assumption prevents R1 firing. As a
consequence, the predicate Sunny will not be in the database and this
prevents R3 firing. At this point where rules have fired as often as
they can, then step (e) of the algorithm (rewritten above) checks consistency.
As, in addition, there is neither inconsistency among the assumptions nor has
the false (^) predicate been generated, the simulation is
stopped. Finally, the logical model generated has the single predicate: Rainy
4th
Example. Introducing the meta modules (an agent in SDML) as a module that can
use the rulebase of other modules (agents) as its database
Assume that the following rule is in the rulebase of the
module meta, which is part of the module prover, and so can write
rules into the rulebase of this module (i.e., into the module prover’s
rulebase):
R1:
{
{
(antecedent of the rule)
clauseList
?antecedent [true];
clauseList
?consequent1 [P(a)];
clauseList
?consequent2 [P(b)];
clauseList
?consequent and [?consequent1 ?consequent2];
namedInstance
?rule RuleName ‘R1-1st example’
}
=>
{ (consequent of the rule)
rule
?rule ?antecedent ?consequent
}
This rule R1 in meta will write in prover
the rule (named ‘R1-1st
example’):
R1-1st example:
True => P(a) ^ P(b);
In the following, it will be explained how this rule works.
There (in R1) the predicate clauseList is used
to build clauses in SDML (the clause created might consist of only one
predicate). The first element is the name of the variable where the created
clause is going to be kept. The second element is the name of the predicate.
The third one, if given, indicates the operator to be used for concatenating
the clauses to be used to create the new clause. These clauses to be used to
create the new clause are listed as the fourth component of this predicate. The
example given by its application in rule R1 will make its use clearer:
In R1, first the predicate clauseList applied in the clause:
clauseList
?antecedent [true]
assigns to
the variable ?antecedent the predicate true. This will be
used as the antecedent of a rule to be created.
Then the
same predicate is used to add to the variables ?consequent1 and
?consequent2, the respective predicates P(a) and P(b).
Afterwards
the same predicate is used to conjunct the content of these two variables into
a new clause; the variable is called ?consequent and the result would be
P(a) ^ P(b). This result will be used as the consequent of the
rule to be created (R1-1st
example) by R1.
Then, an instance of rule is
created using the SDML’s predicate namedInstance. There the following
elements appear:
- ?rule: the name of the variable
the module uses to identify the created rule.
- RuleName:
the name of the standard object used in SDML to identify the type of data
‘rule’.
- ‘R1-1st example’: the name given to the rule to be created. It will be the name
the rule will have when written in the rulebase of prover.
Bringing the strands together
All these features of the inference mechanism that SDML
presents are shown in Figure
5.11, where can be seen on the left side the controllers
of the whole system: the inference engine, which gives the core control of the
system and is a built-in mechanism the usercan not modify; and a meta module
(programmable as a meta-agent), which the user can employ to write rules after
the simulation has started. These two parts are responsible for building (in
part) and partitioning the rulebase, carrying on the simulation (by using the
rulebase), backtracking and assumption manipulation, and managing the database.
In the right part of Figure
5.11, we can see the rulebase written by the user and by
the meta-agent (programmed by the user), as well as the database and the
assumption set. The database contains the facts that are true when the
simulation is going on. The rulebase is partitioned in accordance with rule
dependencies.
|
|
Figure 5.11. SDML’s inference mechanism
|
Assumptions consist of indexes placed to data conditionally
valid, e.g., links specifying the conditions under which data is contingently
valid. Thus if an assumption becomes false while the simulation is going on,
data supported by the assumption is discarded and the simulation backtracks to
the point where the assumption was generated.
We intend to transform a MAS-based
model into a model with a single DB-RB pair. This can be seen as a sort of
‘compilation’ process, which undoes the agent encapsulation allowing a more
efficient exploration of the total system behaviour. The technique was applied
to a simulation model originally built in SDML and is intended to be an example
of proving tendencies in a MAS-based model, and particularly an illustration of
the translation procedure. This translation will be accomplished in two steps.
First, hidden rule dependencies will be revealed, after which, in order to deal
with a certain problem to be explained below, a second step is carried out,
namely an unwrapping of dependencies.
The dependencies in a MAS built in
SDML are hidden in the hierarchies of agents (each agent has its own DB-RB),
modules, and time levels (see upper left side of Figure 5.12). First, the hierarchy of agents consists in
sub-agents contained in other agents. Sub-agents’ rules for a certain time
level fire after the rules of its container-agent, updating data for the same
time level. This gives an order to how rules are fired and, hence, some
dependencies between container’s rules on the one hand and sub-agents’ rules on
the other. Second, time levels give an additional order among rules. For
instance, if there were the time levels month and week, rules of
an agent in time level month would fire before rules of the same agent
in time level week. In addition, rules in time level week would
fire several times (e.g., for each simulated week in a month) to
update data valid for a week before rules updating data for a month
fire again (this can be seen in the predicate and rule shown in the left side
of Figure 5.12).
For the first task, i.e., to reveal hidden dependencies, we
will translate the MAS into a single DB-RB pair. For a signature (namely each
rule, each type of predicate, or function) and each instance of data generated
during the simulation in the MAS model, there will be an equivalent signature
and data instance in the new model (see the illustration in the right side of Figure 5.12). Nevertheless, the structure and dimension of
predicate and function constants in the new (simulation) model are expanded as
fields are added in order to explicitly refer to agents, objects, and time
levels that were previously implicit in the MAS structure. This is shown in Figure 5.12. When eliminating the hierarchies of agents and time
levels in SDML, the agent where the datum was placed in the MAS model and the
time level the datum is valid for, which are implicit data in the MAS model,
have to be referenced explicitly. So, for instance, predicate price in the MAS
model Price(?amount) becomes, in the new simulation model,
Price(?amount,?Trader,?iteration). The last two fields are added to
reference explicitly to the agent and the time level.
|
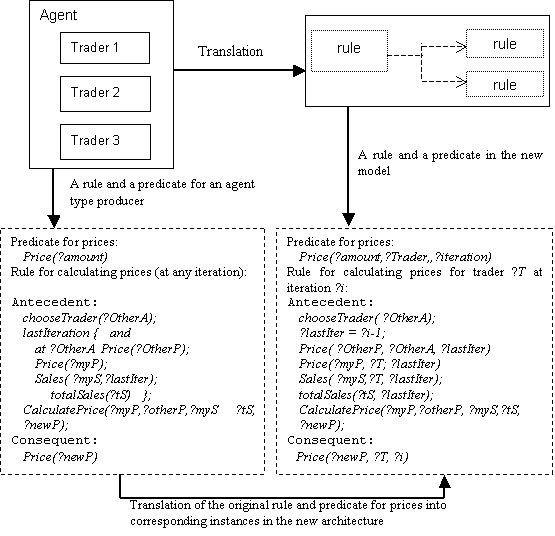
|
|
Figure 5.12. Illustrating how agents and time levels become
explicit in the new architecture
|
For the first task, i.e., to reveal hidden dependencies, we
will translate the MAS into a single DB-RB pair. For a signature (namely each
rule, each type of predicate, or function) and each instance of data generated
during the simulation in the MAS model, there will be an equivalent signature
and data instance in the new model (see the illustration in the right side of Figure 5.12). Nevertheless, the structure and dimension of
predicate and function constants in the new (simulation) model are expanded as
fields are added in order to explicitly refer to agents, objects, and time
levels that were previously implicit in the MAS structure. This is shown in Figure 5.12. When eliminating the hierarchies of agents and time
levels in SDML, the agent where the datum was placed in the MAS model and the
time level the datum is valid for, which are implicit data in the MAS model,
have to be referenced explicitly. So, for instance, predicate price in the MAS
model Price(?amount) becomes, in the new simulation model,
Price(?amount,?Trader,?iteration). The last two fields are added to
reference explicitly to the agent and the time level.
After the rule in the two implementations is illustrated in Figure 5.12, in Figure
5.13 the aspects that make iterative the rule in the MAS
system (shown in the left side of Figure
5.12), as well as the origin of rule dependencies, are
exhibited. Notice that a single rule is used; i.e., it is applied at all
transitions. Also, observe that references to instances of agents and
iterations are implicitly alluded to, and, in some sense, ‘hidden’.
The sources of dependencies (the named data now given
explicitly) are shown in Figure
5.14. There, it is assumed a rule for calculating prices
for agent ?T at iteration-i in the MAS model has been transformed
into a rule where the involved agents ?T (the rule’s owner), ?otherA
(an agent chosen by ?T), and the iteration at which the rule is applied
(data from iteration-(i-1) is taken to generate data at iteration-i)
are referenced explicitly.
As
a result of making data in the predicates explicit, some new dependencies between
rules previously ‘screened off’ from each other can be statically recognised.
|
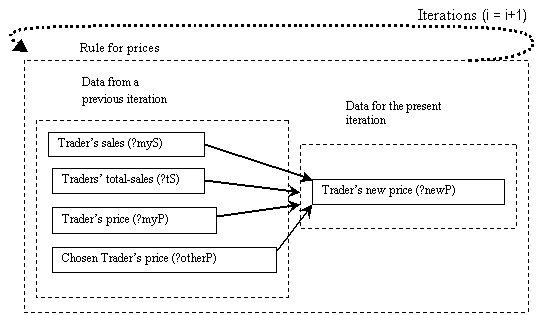
|
Figure 5.13. Showing origin of rule dependencies for the rule
for prices. Dependencies are due only to the iterative character of
the rule
|
|
|
Figure
5.14.
Revealing dependencies, e.g., agent ?T price-setting at time ?i in
accordance with the rule in the right side of Figure 5.12 (?T and ?lastIter create new
dependencies)
|
Nonetheless, a difficulty appears after revealing
dependencies: the space of data a rule searches to check rule-firing grows
linearly with the number of iterations, even though most of the attempts are
failed. This drawback seriously slows down the simulation over time.
The origin of this drawback can be explained using the
example for revealing dependencies given above. Note that it is intended to use
the same rule at any iteration, as was the case in the original MAS. At iteration-1
(e.g., i = 1), the initial data is given, then at iteration-2 rules
use data written for the single iteration-1 and generate data for iteration-2
(see Figure 5.15). There only the references of the predicate price
to agents and to time iterations are shown, indicated only by
numbers (e.g., price(2,1) references price of agent-2 (e.g.,
Trader-2) at iteration 1). After this, the antecedent of the rule
matches data for iteration-i, i=1,2 but it can only generate new data
for i = 2. Similarly, once data for iteration-i, i = 1, 2, …k, has
been generated, the antecedent of the rule matches instances of data for all
these values of i, but it can produce new data only when i = k. As the simulation time goes on, the
simulation slows down because of the discrimination the program has to carry
out among the (linearly) growing amount of data matching the antecedent. In
addition, note that as the same rule is valid for any agent of type A1, the
program has to discriminate among agents. This is another factor that can be
improved where agents are explicitly referenced (in the example it is assumed
there are three agents of type A1, and consequently there will be three
instances of price). In order to deal with these drawbacks, rules are
‘unwrapped’.
|
|
Figure 5.15. The growth of the space of searched data.
Notation: price i, j denotes the price of Trader i at iteration
j
|
Rules will be split for time
iteration and agent. Figure
5.16 shows the splitting of the rule for prices for the
case presented in Chapter 7. When possible, there will be a rule for time
iteration and agent, in order to make the data to be instantiated by the
antecedent of the rule as explicit as possible (see Figure 5.17). Each rule will have an explicit reference to data
given at a previous, or in the present, iteration. For example, in Figure 5.17, where one of the references to price is Price(?myP,
T-2; (i-1), there we can see the explicit reference to a specific agent,
T-2, and to a specific time iteration, (i-1). As can be seen, the
number of rules can by huge as now they are specified by iteration and by
trader (and probably by trader’s choice). An automatic way of doing this
splitting would be helpful.
This process of
splitting needs a semantic manipulation of rules allowing the reference of data
to occur more explicitly. The idea is to instantiate data already set up in the
database or whose introduction during the simulation can be foreseen.
Parameters of the simulation model are an example of data given at the
beginning of the simulation. Choices, like an agent’s selection of another
agent for price imitation, or decisions can also be predicted. This was the
case in the applications.
Compilation of rules can be implemented in SDML using a
meta agent, or a meta module. SDML’s meta module was used in the
case given in Chapter 7 only at the beginning of the simulation. In other
applications, its usefulness would be furthered if it were employed to write
rules while the simulation is going on. It might be used, for instance in an
iteration, for writing transition rules for a next iteration. It might be
helpful for driving the search conveniently, for example, to choose rules to
guide the search according to certain criteria (e.g., as in OTTER when using the weithing
criterion for selecting clasues from the ‘set of usable’). It would also help if it of
interest to elaborate the theorem to be proved during the simulation (e.g., a
theorem defined in terms of an envelope to a certain simulation output).
|
|
Figure
5.16. Splitting of rule for prices
|
|
|
Figure 5.17. Above, ‘unwrapping’ of dependencies is shown.
Below, the data-space searched by the rule-setting for a trader is
illustrated
|
In the light of the discussion so
far, it seems convenient to distinguish and to model as distinct entities three
basic elements of a simulation: the static structure of the simulation
model, that part where parameters and initial data are given; the dynamics
of the simulation where transition rules are fired; and a meta module
responsible for writing transition rules as explained above. Thus, each one is
programmed in a different module, as follows:
model, sets up the structure of the simulation
model, that is, it gives the environment of the simulation: range of
parameters, initialisations, alternative choices, and basic (backward-chaining)
rules for calculations.
prover, generates the dynamics of the
simulation. This is a sub-module of model (i.e., it is contained in model).
This will basically contain the transition rules, auxiliary rules for
generating pre-processing required data, and the conditions to test the
necessity of the theorem. All of them are rules to be executed while the
simulation is going on.
meta, is responsible for controlling the dynamics
of the simulation. Its meta-rules write the transition rules and the theorem in
(as well as others required by) the module prover. A picture of the
system is given in Figure 5.18.
Program dynamics:
Modules are executed in the following sequence (see Figure 5.18):
- model: initialising the
environment for the proof (setting parameters, etc.).
- meta: creating and placing the transition
rules in prover, using data given by model to explicitly
reference instances.
- prover: carrying on the simulation by executing
the transition rules and
backtracking while a contradiction is not found.
The program backtracks from a path once the
conditions for the theorem are verified, after which a new path with different
choices and/or parameters is picked up.
|
|
Figure
5.18. Overview of the efficient
implementation
|
Comparing the original MAS-based
simulation and the constraint-based translation, a speeding up of a
factor O(N), where N
is the average number of agents instantiated by a rule, is gained in the later
implemententation,. Notice that all these values are only estimations
because it is assumed rules give up trying to fire after checking all their
clauses, since in fact a program stops trying to fire a rule as soon as one of
its clauses becomes false. For more details about these estimations, see
Appendix 5. Advantages of this technique for exploring the simulation space of
possibilities, such as making the backtracking more specific and the space of
updated data between backtrackings as small as possible, are also explained in
Appendix 5.
There are additional benefits associated with
the more explicit exposition of the data, as given in a database and accessible
from a meta-module. These may allow the theorem to be established over a range
of theorems as a result of the adaptation of the original specification to the
results of the simulation.
The translation from a MAS-based
model S = <T, X, W, Q, Y, d, l >
to a (logical) model constraint-based model S’= <T’, X’, W’,
Q’, Y’, d’,
l’>
seems to be isomorphic, though the modelling platforms might be
different. For example, in the case study presented in Chapter 7, the MAS-based
model S is implemented in SDML and the (logical) constraint-based model S’
is written in two platforms: in OTTER and in SDML. The comparison is more
direct if the two models are written in the same platform. If S’ is
written in OTTER and S in SDML, the underlying logic of the languages is
different. On the one hand, SDML follows a sort of non-monotonic logic, as, for
instance, it accepts not only two-valued predicates, e.g., predicates that
cannot only be two-valued as true or false but which can also be
assumed as unknown (for instance, those preceded by the predicate not-inferred
(¬)). In addition, in SDML the inference mechanism is driven by a set of rules
following and order given by the rule dependencies. On the other hand, OTTER’s
underlying logic is two-valued; its predicates can only be either true
or false. Besides, in OTTER the search is driven by the set of usable,
which, in the case given in Chapter 7, contains the translation of what in the
original model S (written in SDML) were the rules and the theorem to be
proved. In that case given in Chapter 7, hyperresolution is used to drive the
search. Despite all this, however, the generated simulation is very similar
because of the following reasons:
-
Each rule and each data assertion in S has a corresponding rule or data
assertion in S’ (tough predicates in the (logical) model
constraint-based platform have additional arguments to make explicit the agents,
objects, and time levels).
- Assumptions can be
introduced in OTTER by adding an argument to predicates to keep trace of the
assumptions (as was the case in the application). The split procedure permits
one to create branch points and to choose different alternative values for some
variables (e.g., it allows an agent to choose different agents for behaviour imitating)
via an explicit search.
- The isomorphism function h, as well as the functions g
and k defined in section 2.3.3, would be appropriately defined to filter
the differences between the simulation models given by the addition of
arguments into predicates of S’ to make explicit agents and time levels.
- In the simulation a trajectory in S has an equivalent
trajectory in S’. The state transitions are equivalent. For example, a
state transition in one of the models has an equivalent state transition in the
other model; there should exist a one-to-one translation between the states of
the two systems.
- Because of this,
any proof in S’ (such as that achieved in the case presented in
Chapter 7) is also valid in S. In more general terms S’, seems to
be a valid translation of S under any experimental frame < W, Y, l, V>E.
The isomorphism would be valid under any experimental frame.
Notice that Zeigler was interested in a valid simplification
(see Chapter 2) while in this thesis the interest is more in valid
translations. In both cases, there should exist a morphism between the two
simulation models valid under an experimental frame. However, Zeigler was
aiming at finding a simulation model S’ simpler than the original simulation
model S (it is assumed that a simulation model is a system) in accordance with
a certain measure of complexity, while the interest in this thesis is in
finding a simulation model S’ that is more efficient for proving tendencies
than S. This efficiency is measured in terms of the computational resources the
simulation model requires for exploring a fragment of the simulation theory.
In the (logical) proposed model constraint-based
exploration, the investigated fragment of the theory is defined using a range
of parameters and choices. This new simulation model is more efficient in terms
of its potential for proving than the original MAS-based model. In particular, conclusions
from a (logical) model constraint-based exploration defined by a range of
parameters and choices are valid for both simulation models in the experimental
frame < W, Y, l, V>E (for an explanation of this
terminology, see section 2.3) where the set V contains the range of
constraints (parameters and choices) defining the subspace of explored
simulation trajectories. V is the key variable for defining an
experimental frame. Notice that V also defines the explored fragment of
the simulation theory.
Nevertheless, the new architecture might be less appropriate
for purposes other than theorem-proving. For example, an efficient simulation
model for proving might give less detail about the simulation. This is not the
case for this (logical) model constraint-based architecture as it explores each
simulation trajectory. Nevertheless, the information it generates might not be in
an easily understood format. For example, the links between data and agents
might be subtle and more difficult to understand, as more of the references in
the rules have to be managed by the user himself rather than being implicit in
the structure of the MAS-based model. Similarly, it might be more difficult to
program the output a modeller requires.
Summing up, the simulation model in the
(logical) model constraint-based architecture seems to be equivalent
(isomorphic) to the MAS-based model. The proofs it offers seem to be valid in
both simulation models under the experimental frame and for the fragment of the
theory defined by the range of parameters and choices determining the subspace
of trajectories to be explored.
The two architectures of programming
described above, namely a MAS-based model and a (logical) model
constraint-based architecture, are both logical model-oriented; the dynamics of
a trajectory are generated explicitly. Because of this, the needed amount of
computational resources is huge. The second architecture adds efficiency to the
search and allows restricted proofs of tendencies. Nevertheless, it would be
convenient to explore other alternatives, in a search for even more efficient
procedures for proving tendencies in a simulation. Syntactic manipulation of
rules and constraint logic-programming are areas of knowledge showing potential
for assisting in this task. This section suggests the investigation of methods
related to these two approaches and speculates about morphism between a
MAS-based model and a hypothetical syntactic constraint-based model (for more about a syntactic constraint-based
architecture, see Chapter 6).
One of the factors making the comparison between the above
(simulation) models S (the MAS-based model) and S’ (the logical
model constraint-based model) less difficult than the present one is that the
two architectures offer a logical model-based exploration of the dynamics of a
simulation. If we were translating the simulation model into a more
syntactic-based exploration (given a simulation model S’’= <T’’, X’’, W’’,
Q’’, Y’’, d’’,
l’’>),
then not all the semantics of the simulation would be explicitly generated and
the comparison would not be so direct.
Similar to the translation to a constraint-based logical
model search, if the aim is facilitating theorem-proving, the translation
should be homomorphic under the experimental frame defined by < W, Y, l, V>E,
where V is a set containing the range of parameters and choices for
which the dynamics of the simulation are going to be explored. However, the
functions h, g, and k would be more difficult to define.
Here, neither do all the semantics of the simulation have to be generated, nor
does a one-to-one correspondence between the original simulation model S and
the new simulation model S’’ necessarily exist. For example, the
set of transition states in the simulation models, W in the MAS-based
model and W’’
in the constraint-based syntactic model, might be different. In constraint
logic-programming (see section 3.7), notions different to unification are
applied for firing rules. Advance in the search, i.e., a state transition in W’’,
might be due, e.g., to a syntactic manipulation implicitly involving a range of
semantic values (perhaps a range of choices or a range of parameters)
associated to the state of the system at different time instants (this is
different in a semantic search where each possible world or logical model is
explicitly generated). This means that a syntactic state transition in S’’
might resume changes corresponding to several state transitions when using only
unification and exploring single simulation trajectories (this is the case in a
logical model constraint-based architecture and in a MAS-based simulation). A
search in S’’ will hopefully be cheaper in computational terms and more
efficient for proving than S’ and S (for more details about this proposed
architecture, see Chapter 6).
In this chapter a hierarchy of
architectures for improving the understanding of MAS-based simulations of
complex systems is proposed (this hierarchy is illustrated in Figure 6.1; a discussion about what we mean by a subject’s
understanding and how it changes as the modeller’s experiences with a simulation
model was given in section 5.6). This will go further than the constraint-based
architecture proposed in Chapter 5. The idea is to provide modellers with
several architectures informing them about complementary aspects of the
MAS-based simulation. They will each have different modelling purposes. The
level of programming, the searched space of trajectories, and the power of the
conclusions drawn at each level will be different. In addition, in the following
discussion, the advantages of investigating MAS dynamics through such
transformations, using a mechanism allowing such a translation automatically,
or semi-automatically, and interactively will be highlighted.
The main intention of this hierarchy of architectures is to
help a modeller to search, identify, and prove tendencies in a MAS-based
simulation (this is represented as the level of single exploration in Figure 6.1). For searching tendencies, a high architectural
level is proposed. It is intended to assist the modeller in capturing relevant
macro aspects (tendencies) of the simulation phenomena. It allows an active
participation of the modellers in order to identify tendencies they are
interested in. The idea is to exploit those capabilities that make MAS a
special paradigm for generating macro aspects of phenomena at a high level in a
way that is easy for the modeller to understand and easy to associate with what
he observes in the modelled system. Additional details about the advantages of
this architecture are given in section 6.2.
After some tendencies have been identified in a MAS, a more
careful (systematic) exploration of trajectories and investigation of
tendencies might be implemented using a (logical) model constraint-based search
under a relevant range of parameters and choices, such as that proposed in
Chapter 5 (this is represented by the intermediate level in Figure 6.1). This search will be complete for certain ranges of
parameters and choices. It will help a modeller to do scenario analysis, as the
exploration is logical model-oriented (the semantics are shown), as well as to
execute proofs over restricted domains. The advantages of this architecture are
summarised in section 6.3.
Ideally, we would be able to provide a modeller with an even
lower level of programming (see the lowest level in Figure 6.1). That would be a third architecture, proposed in
section 6.4, aimed at increasing the potential for proving. This would be a
syntactic procedure. At this level proofs for a wider range of parameters and
choices and/or for a longer time period (a larger number of time steps) than in
the previous level would be possible. The proof procedure will be, on the one
hand, subtler from the modeller’s point of view but, on the other hand, the
results will be more powerful, permitting the modeller to elaborate more
general conclusions.
|
|
Figure 6.1. Sequence of modelling architectures
|
The idea is not to move only in one direction in this
hierarchy. Going down from a higher level of programming towards a lower one
might be useful for proving tendencies already observed in a higher level.
Likewise, going up to a higher level of programming will help the modeller
understand aspects related to the proofs he has achieved in a lower level.
To close the
chapter, in section 6.5, different aspects of a simulation that each
architectural level informs about and the complementariness of this information
are highlighted.
Examples of applications where architectural
transformations would be useful are found in the social simulation community.
In Axtell et al. (1996), alignment of
models is proposed as useful for comparing models and the theories behind the
models. Those compared models might represent different architectures. Models
in the different architectures might represent aligned models. Moss (1998)
compares several MAS modelling approaches in social simulation. It would be
useful to have an automatic ‘translator’ of models in different architectures
for assisting a modeller when doing this sort of comparison.
The idea here is to execute a MAS-based exploration of
simulations in a modeller’s search for tendencies by inspecting single MAS
trajectories. A MAS offers a high level programming paradigm giving and
appropriate environment to observe agents’ interactions. A MAS provides
facilities to program interacting agents as observed in the empirical system.
In advanced MAS, like those that can be written in languages such as SDML, both
data and behaviour are conveniently distributed in the hierarchy of agents.
A
MAS allows the modeller to trace both the quantitative and qualitative
evolution of the agents’ interaction. Hopefully, the level of phenomena
observable in MAS allows a modeller to find emergent tendencies, some of them
resembling emergent behaviour that is also recognizable in the empirical
system. A further investigation of an emergent tendency can be done by
translating the simulation model into a lower level of programming than a MAS.
The idea at this point is to allow a wider exploration of simulation
trajectories as well as a broader investigation of fragments of the simulation
theory. An example of architecture at a lower level of programming than MAS is
that given in Chapter 5 (e.g., the
(logical) model constraint-based architecture). The next sections will outline
a hierarchy of architectures that includes these two levels and a possible even
lower architectural level.
For this level an efficient
(logical) model constraint-based exploration is proposed. An example of this
sort of architecture was given in Chapter 5 using a logical model-based,
clausal ordered exploration with a forward-chaining inference procedure, and a
case is presented in Chapter 7. The idea is to explore each logical model of a
fragment of the simulation theory and prove facts when possible.
In those chapters (5 and 7), the feasibility of this idea
and a technique for its implementation are illustrated. Such architecture is a
lower level of programming than a MAS. The hierarchy of agents disappeared as
the simulation model consisted in a single DB-RD pair. At the MAS programming
level, a modeller is better informed about the explored trajectories, as he can
more easily follow over time the evolution of the agents’ interaction for each
trajectory. This new architectural level was intended to allow constrained proofs
of tendencies. Hopefully, it will help a modeller to understand better the
dynamics of a simulation model (and hence of a target system). At this
intermediate second level of programming, the modeller is less informed about
individual trajectories, but he obtains information from a wider space of
trajectories than a MAS can explore about a specific theorem. However,
information about a fragment of the whole theory embedded in the simulation
will be collected. The proposed technique can be seen as falling in between
inspecting single runs in a logical model-based exploration of trajectories and
syntactic theorem-proving.
The proposed architecture enables a modeller to implement a
complete logical model exploration of the dynamics of a simulation for a range
of parameters and choices though encoding it in a lower information level than
that which a MAS offers. It allows a modeller a different trade-off between two
characteristics of the information the architecture provides a modeller: the
size of the explored simulation theory and the detail of data in a trajectory.
In this sense this architecture is complementary to a MAS.
After experimenting in a constraint-based architecture, a
modeller might find it worthywhile to go back again to the higher level of programming
again to increase the understanding of proved tendencies, as this gives more
detail about the agents’ interaction. That is because simulations at the higher
MAS level are less complex from the modeller’s point of view and are generally
more helpful for increasing understanding of macro aspects of a simulation.
Given the difficulties for
implementing a logical model-based constraint search (principally that the
amount of data generated is huge), it would be convenient to implement an even
lower level of programming: one more efficient for implementing proofs (though
probably particular details of the search process become less meaningful for a
modeller). Specifically, we propose a syntactic constraint-based exploration of
the simulation theory.
This level would be similar to
the logical model constraint-based architecture in the sense that the
exploration would be constrained by the range of parameters and choices. It
would be different to this architecture (and to the MAS-based model) because
the search would be syntactic-based rather than logical model-oriented. A
syntactic method would be based more on the syntactic manipulation of elements
of the simulation rather than in the semantics of the simulation. The two
methods given above generate explicitly all the semantics of a simulation; each
trajectory is explored at a time. The idea at this level would be to explore
the relevant aspects of the simulation theory in a more efficient way. It is believed that constraint
logic-programming is an area where helpful ideas could be found (see Chapter
3).
To clarify the idea of efficiency
behind the proposal when compared to a logical model-based exploration,
consider an example of numerical mathematics. In example
6.1 we will compare a numerical manipulation (a kind of logical
model-oriented strategy) with an algebraic manipulation (a sort of syntactic
approach).
Example 6.1.
Assume it is intended to prove the proposition P under
the constraints c1 and c2:
P: X + 100 < Y
c1: X = 1, 2, …, 80; c2: Y = 200, 201, …, 1 000
First, numerical manipulations (following the logical model
approach) are used. For proving the proposition, each of all possible values
for (X, Y) is chosen. In total, there are: 80 * 800 = 64 000 possible
combinations (these possibilities are: (1, 200), (1, 201), …(2,200), (2,
201), …, (80, 200), (80, 201), … (80, 1000)). After all possible
substitutions of the variables have been examined, the proof is done. In this
case a lot of manipulations are needed and all possible semantic values of the
variables have to be explicitly tested.
Now, assume that algebraic
manipulations are allowed in a syntactic attempt to prove P. In this
case, algebraic axioms are used for reasoning. First, the axiom a1
given below is used.
a1: for all integers X, Y, Z: X + Y < Z if and
only if X < Y – Z
By a1,
the proposition P becomes: P: X
< Y – 100
Now suppose we use another axiom, a2:
a2:{ if
{( Xmax = Maximum of the
values X can take) and
(Ymin = Minimum of the
values Y can take)}
Then X < Y – Z if Xmax <
Ymin - Z}
Using this axiom the proposition P is true if the
following proposition P’ is true:
P’: 80
< 200 – 100 = 100
Clearly P’ is true (80 < 100),
hence also P is
true.
This second proof is more efficient than the
logical model-oriented one, as the syntactic approach permits one to achieve
the verification without the need for generating explicitly all the semantics of
the variables. This is the sort of advantage that would be won if using a
syntactic oriented architectural level for proving tendencies in a simulation.
In a syntactic exploration of a simulation theory, on the
one hand, it might be more difficult for a modeller to find a satisfactory
explanation of proved tendencies and other macro aspects of the simulation. On
the other hand, however, it might be more powerful by proving in the sense that
it would allow the relaxation of bounds imposed over the search, namely the
limited range of parameters, choices, and/or time iterations.
It is believed this can be implemented via
syntactic backward-chaining inference manipulations. The idea is to prevent
exploration of each single logical model and, consequently, the need to lay
down explicitly all the semantics of the explored trajectories (which is
computationally expensive), and instead to explore a subset of trajectories in
a more concise manner (as in example 6.1). The plan is to implement the
syntactic manipulation of rules with an implicit introduction of constraints.
More concretely, the conditions established by experimenting with logical
model-based exploration would need to be added to the MAS specification and all
this translated into axioms for a syntactic theorem-prover to work upon. In
this sense, less data would be generated and less manipulation necessary than
in the two higher levels of programming.
Compared with the two previous methods, this approach would
offer a user a different trade-off between the level of detail of information
and the scope of the exploration. The user would find it more difficult to
understand particular results the method gives, but the conclusions it allows
would be valid for a larger fragment of the simulation theory. This
architecture might be used interactively with the others; after some proofs a
user might go back again to a higher level in order to explore aspects related
to which the proved tendencies he wishes to understand better.
|
ASPECT
|
SCENARIO
ANALYSIS
|
LOGICAL
MODEL-EXPLORATION
|
SYNTACTIC
PROOF
|
|
Typical paradigm
|
Imperative
|
Constraint
|
Declarative
|
|
Typical deduction system
|
Forward-chaining, logical model-oriented
|
Forward-chaining using
efficient backtracking
|
Backward-chaining or resolution-based
|
|
Nature of the manipulations
|
Possibly semantic
|
Range of semantics
(logical model)
|
Syntactic
(clausal-ordered)
|
|
Limitations
|
Not constrained.
Very rich. Too much
information could mislead.
|
Finite constrained. Still
quite rich.
Suitable for scenario
analysis.
|
Constrained.
Valuable for proving
specific tendencies.
|
|
Search style
|
Attempts to explore all
simulation paths.
|
Limits the search by
constraining the range of parameters and agent choices.
|
Can be efficient in suitably
constrained cases, typically impractical.
|
Table 6.1. A
Comparison of the Architectures
The main aspects distinguishing the
architectural levels are the generality of the allowed conclusions and the
level of programming. The higher the architectural level, the more a subtle
design and dynamics can be practically supported; but the easier it is to
understand the generated dynamics, the more general are the conclusions that
can be drawn. This process has been illustrated in Figure 6.1 above.
A modelling process where a modeller uses all three
architectures interactively is exemplified in Figure
6.2. Some of the benefits of a mechanism allowing an
automatic translation among these architectures are improving understanding of
and better informing a modeller about the dynamics of a simulation. A modeller
moving among architectural levels according to interest, learning, and
experience would benefit greatly.
|
|
Figure 6.2. Interactive use of the architectures by a modeller
|
The aim of this chapter is to
communicate the experience of developing the methodology presented in Chapters
5 and 6. Details of the simulation case and its different implementations in
SDML and OTTER will be presented.
The example consists of a trader-distributor (simulation)
model with six agents: three traders and three distributors. The agents’ main
tasks are: for traders, price-setting, price-imitating, and sale-setting; and,
for distributors, order-setting. The example resembles basic characteristics
that can be observed in many empirical systems, but it is ideal in the sense
that it is not a representation of any particular empirical system. The idea
has been to elaborate a typical simulation model to develop the methodology for
exploring the dynamics of MAS-based simulations.
The first model (we use the world model for simulation
model) is a MAS-based model built using the language SDML. Basic aspects of
this model are presented in section 7.2. This model is used to explore the
dynamics of the simulation. At this level the idea is to explore the dynamics
by generating trajectories at a high level of programming, since a MAS is an
architecture which gives detailed information about individual trajectories.
This experience is discussed in section 7.3. A tendency concerning the
behaviour of prices is observed in the MAS-based simulation. This tendency was
expressed as an envelope rather than as a central measure, as would occur if
Monte Carlo techniques were used. How the tendency was enveloped is reported in
section 7.4.
A MAS level of programming can provide rich information
about the evolution of state transitions in each trajectory. However, it is
difficult to prove the commonality of a particular tendency over a range of
trajectories. Because of this, a different architecture of programming, namely
a theorem-prover, is chosen for attempting to prove a tendency in a simulation.
Among several theorem-provers available, OTTER seems to be one of the more
suitable for this task because of its success in other areas of research and
because it presents more facilities for numerical manipulations (arithmetical
manipulations are common in simulation of social systems) than other available
theorem-provers (e.g., among the facilities are demodulators; see Chapter 3).
The experience from a first attempt to prove the tendency is
offered in section 7.5. A translation that seems to be isomorphic to the MAS
model is built in the theorem-prover OTTER (why it is believed that the
translation is isomorphic is explained in section 5.10). A more exhaustive
investigation of the dynamics of the simulation is carried trough in an attempt
to prove the necessity of a tendency for a range of trajectories. Though OTTER
supports these sorts of proof, it is not totally appropriate. On the one hand,
OTTER (like most of the existing theorem-provers) is oriented at proving in
first-order logic via symbolic manipulation. However, on the other hand, it has
poor user interface, limited facilities for numerical manipulation, and does
not permit change over the structure of the model or meta-reasoning while the
simulation is going on. As was noted in Chapter 3, OTTER is not flexible for
user-driven manipulations of the database and rulebase.
It seems convenient, then, to attempt the
proof in a more suitable language allowing not only a more flexible
manipulation of data and rules, but also the implementation of a proof
procedure close to that followed in OTTER. For instance, the idea is to take
advantage of a proof procedure like that implemented in the OTTER model and of
facilities that a higher architecture of programming offers. This is also
convenient because a common platform is necessary if we wish to implement
automatic translation of a model among different architectures. We choose SDML
as that language. SDML offers a meta-agent to write rules on other agents.
Also, SDML tenders facilities for a wide range of data manipulation and for
implementing proofs. Some facilities for proving that were initially not
present in SDML were added (e.g., false predicate in the consequent). Section
7.6 reports these SDML features.
Section 7.7 presents the first attempt to prove in SDML. In
this first effort drawbacks in data manipulation, inherited from the MAS
implementation, were found to slow down the simulation. These drawbacks are
referred to in section 7.8 and have already been explained in section 0. Then a more efficient structure was implemented to
deal with these drawbacks. Generalities of this architecture are given in
section 7.9, as a more detailed review was already presented in section 5.9.3.3.
These proofs in SDML and OTTER are examples of the
constraint-based logical model exploration of a simulation proposed in Chapters
5 and 6. This represents a lower architecture of programming than a MAS-based
model.
A comparison between the MAS-based and the (logical) model
constraint-based architectures is presented in section 7.10. Characteristics of
the information each architecture provides with respect to a simulation
trajectory and to the whole simulation theory, as well as the allowed scope of
the conclusions drawn from that information, are emphasised.
In section 7.11 the importance of both studying the dynamics
of a MAS and proving tendencies in a constraint-based architecture, for a
modeller’s understanding of tendencies in a simulation, will be addressed, and
special consideration will be given to how this analysis relates to the notions
of a subject’s explanation and understanding discussed in section 5.6.
Finally, in section 7.12, the (logical) model
constraint-based approach will be contrasted with other procedures used for
exploring the dynamics of simulations and for theorem-proving.
The first model was a MAS-based one,
built using the language SDML. The more relevant aspects of this model are
shown in Figure 7.1. There are six agents: three distributors and three
traders. The agents’ main tasks are: for traders, price-setting,
price-imitating, and sale-setting; and for distributors, order-setting. In
addition to the agents some objects are used representing the traders’
warehouses. The dynamic structure of the model is represented using rules and
the static structure, in part, via predicates, objects, and agents.
The facilities SDML offers for modelling MAS include those
for manipulating agents, time levels, and modules hierarchically. The hierarchy of agents is useful for
representing agents as sub-agents contained in other agents. A sub-agent
inherits facilities and properties such as predicates, clauses, and types of
objects from its containers. The hierarchy of time levels is helpful for
writing data valid for periods of time of different length. For example, if
there were the time levels ‘week’ and ‘day’, there would be some transition
rules for updating facts valid for a whole ‘week’, and other rules for updating
data valid for only a ‘day’. A hierarchy of modules is valuable for defining
modules at different levels, where those at a lower level are more basic than
those at a higer one. Those at the lower level will be used for defining more
basic types of agents and objects to be used by the modules at the higher level
for defining more complex entities.
Using these hierarchies, certain
information is given implicitly. For example, there might exist (internally in
SDML’s design) an indexation of data per agent and time level, so that it is
not necessary to indicate these explicitly at each predicate during the time
period it is going to be valid for and at the agent holding it, but it will be
enough to place it in the appropriate area of a database. If the instance of
price, Price(10),
is placed in the database of Trader-1 in the sub-area of data for time levels week
= 3, day = 2, it would mean that agent Trader-1 has set his
product’s price at value 10 on day 2 of week 3. This is an
example of how the hierarchy of time levels and agents hides data (making
explicit this data would create additional rule dependencies; see Chapter 5
and, more specifically, section 5.9.2).
The main predicates used in the
model are listed below along with their domain. Predicates represent
relationships among agents and/or objects. For example, the predicate
sale(Trader,
Distributor, Amount)
is used to indicate the Amount of good a trader, Trader, sells to
distributor, Distributor. Below, a list of the most significative
predicates used in the model is given. There it can be seen that the sale predicate is
placed at agent Model. The arguments of the predicate are: the two
agents involved in the transation, e.g., Trader and Distributor, and the Amount of good sold.
If this predicate had been asserted in agent Trader, the explicit reference to this agent would not have
been needed.
|
|
Figure 7.1. An overview of the model
|
Model (general or
environmental variables):
listChoiceTrader(Trader,
Trader,Trader, i);
Description: gives the choices of traders to be used in price-setting.
Element-j in the list is the choice for trader-j at day i. There will be eight
of these predicates per day (the eight different choices).
listSelTrader(Trader,
Trader,Trader);
Description: lists the traders ordered by their prices. It is used for
calculating the amplitude of the interval of the prices and for a distributor
placing orders (they place orders to the trader with the lower price).
order(Distributor, Trader, Amount);
Description:
Amount is the quantity orderer by distributor Distributor at
trader Trader. The time (day) is implicit, that is, there will be one of
this predicate per iteration (day). This will be a fact in the following cases.
orderDistributor(Distributor,
Amount); (total order the distributor places among all
traders);
Description: Amount is the total quantity of good an agent Distributor places
at current time (day).
orderTrader(Trader,
Amount) (total order a trader has from all
distributors);
Description:
Amount is the total quantity of good ordered by all distributors from trader Trader.
sale(Trader, Distributor, Amount);
Description:
Amount is the quantity of good trader Trader sells to
distributor Distributor,
at current time.
listSelTrader(Trader,
Trader,Trader);
Description: places the traders in order accordancing to their prices
(one listed earlier has price lower than or equal to that of one listed later).
This is used for calculating the amplitude of the interval of the prices and
for distributors placing orders (they place orders to the trader with the lower
price).
Trader:
price(Value);
Description:
Value
is the price trader Trader gives to his
product at current time.
saleTrader(Amount); (total sales
the trader makes in a day);
Description: Amount is the total sales trader Trader
makes at current iteration.
Distributor:
Demand(Amount);
Description: Amount gives
the total demand distributor Distributor has at current time.
saleDistributor(Amount); (total sales
made to this distributor by all traders).
Description: ‘Amount’ gives the
total quantity of sales made to distributor Distributor at current day.
supply(Amount); (it resembles a factory production).
Description:
Amount gives the quantity of good the Trader
owner of the warehouse Warehouse gets at the current iteration.
Warehouse:
level(Amount);
Description: Amount indicates Warehouse’s
level of good.
All rules are supposed to generate data for the present
iteration at which the simulation is going on, unless the contrary is
explicitly specified (the present iteration will be called ?i in some rules, but it is usually referenced
implicitly). The previous iteration is referenced as lastIteration. In the model, a
rule is always part of an agent rulebase and it will write, by default, data in
the dababase of that agent.
1) Rules
in the environment given by the agent Model
1.1) Rule used by a trader for choosing another trader for
price-setting
This
iterative rule makes a choice for iteration ?(i+1) after the choice for iteration ?i has been made. It divides the task
of making the choices for the whole simulation to one per day, which helps in
decreasing the computational complexity of this task.
Antecedents:
and
listChoiceTrader(?previousChoice, ?i);
{instantiates choice for iteration ?i}
randomChoice ?randchoice
?allchoices 2
listOfPossibleChoices ?allchoices;
{number 2 is a randomisation factor }
{traders’ choices are listed below in
section 7.2; this clause gives alternatives when the
system backtracks after the theorem has been
proved in a trajectory }
Consequents:
listChoiceTrader(?randchoice,?i+1);
1.2) Rule for creating a list of
traders ordered according to the prices they offer
Antecedents:
backSelProd(?i =
?currentIteration, listSel);
{this
backward-chaining rule orders the traders according to their prices at
iteration ?i and returns them in the list ?listSel }
Consequents:
listSelProd(?listSel );
1.3) Rule for calculating
distributors’ and traders’ total orders
Antecedents:
and
order(Distributor-1,Trader-1,?s1);
order(Distributor-2,Trader-1,?s2);
order(Distributor-3,Trader-1,?s3);
order(Distributor-1,Trader-2,?s4);
order(Distributor-2,Trader-2,?s5);
order(Distributor-3,Trader-2,?s6);
order(Distributor-1,Trader-3,?s7);
order(Distributor-2,Trader-3,?s8);
order(Distributor-3,Trader-3,?s9);
?order1 = ?s1 + ?s4 + ?s7;
?order2 = ?s2 + ?s5 + ?s8;
?order3 = ?s3 + ?s6 + ?s9;
?ordert1
= ?s1 + ?s2 + ?s3;
?ordert2
= ?s4 + ?s5 + ?s6;
?ordert3
= ?s7 + ?s8 + ?s9;
Consequents:
and
orderDistributor(Distributor-1,?order1);
orderDistributor(Distributor-2,?order2);
orderDistributor(Distributor-3,?order3);
orderTrader(Trader-1,?ordert1);
orderTrader(Trader-2,?ordert2);
orderTrader(Trader-3,?ordert3);
1.4) Rule for calculating
traders’ total sales
This rule calculates ‘totals’ in a similar way to the
rule listed above, and generates the data in the predicates: saleDistributor(Amount)and saleTrader(Amount) (the former predicate is placed at the
distributor’s rulebase and the second at the trader’s rulebase, which is why
such agents are not explicitly given in these predicates).
1.5) Rule for theorem-checking
The hypothesis we have attempted to prove is: the
amplitude of the interval of prices does not increase over time for the
iterations (1,…,k) as the simulation is
generated. If the theorem is true in a simulation trajectory, the predicate
false is generated and the system backtracks to explore another
simulation trajectory.
Antecedents:
and
calculateAmplitudeIntervalPrice(1,?amIntPrice1);{1: stands for
the iteration}
calculateAmplitudeIntervalPrice(2,?amIntPrice2);
...
calculateAmplitudeIntervalPrice(k,?amIntPricek);
notInferred greaterOrEqueal ?amIntPrice2 ?amIntPrice1;
notInferred greaterOrEqueal ?amIntPrice3 ?amIntPrice2;
...
notInferred greaterOrEqueal ?amIntPricek ?amIntPricek-1;
Consequents:
false
2) Rules
in the agent type trader (traders are sub-agents of the agent Model)
2.1) Rule for traders’ price-setting
Antecedents:
and
lastIteration {and
saleTrader(?mysales);
totalSales(?totalSales);
price(?oldprice);
}
listChoiceTrader(?choices, at ?i = currentIteration);
?choices = [?sel1
?sel2 ?sel3]; {Trader in
position k in this list is the choice
for
trader with name ‘Trader-k'}
otherPrice(?otherprice,?choices,?i,self
{sending its name});
{Knowing
the trader, the rule is calculating the price for (e.g., Trader-j), the
iteration (?i), and
the list
of choice of traders (the choice for distributor-j would be ?selj), this
backward-
chaining rule returns the price of the chosen trader
(i.e., at (?selj,?i) it gets price(?otherprice);
calcprice(?newprice,[?oldprice ?otherprice ?mysales, ?totalSales]);
Consequents:
price(?newprice);
{if the agents and the iteration were explicitly
referenced, the rule would be (after the appropriate
changes
in the definitions of the predicates):
Antecedents:
and
saleTrader(?Trader,?mysales,?i);
totalSales(?totalSales,?i);
price(?Trader,?oldprice,?i);
listChoiceTrader(?choices,?i);
?choices = [?sel1 ?sel2 ?sel3];{Trader
in position k in this list is the
choice for
trader with
name ‘Trader-k'}
otherPrice(?otherprice,?choices,?i,?Trader);
{Knowing the trader the rule is
calculating the price for (e.g., Trader-k), the iteration (?i), and
the list of choices of traders, this backward-chaining rule returns the price of the
chosen
trader at
iteration ?i (e.g.,
price(?selk,?otherprice,?i));}
calcprice(?newprice,[?oldprice
?otherprice ?mysales ?totalSales]);
Consequents:
price(?Trader,?newprice,?i+1);
{this is the sort of transformation that
will be necessary if the hierarchy of agents and time levels is eliminated, as
will be seen below} }
2.2) Rule for traders’
sale-setting
Antecedents:
and
level(?level); {in fact, level is consulted at the
trader’s store’s database}
order(?Distributor,?Trader,?orderDistTrader);
orderTrader(self,
?orderTrader);
calcSale(?level,?orderTrader,?orderDistTrader,?sale)
Consequents:
at Model write:
sale(?Trader,?Distributor,?sale);
2.3) Rule for trader’s production (or supply) and level updating
Antecedents:
and
lastIteration {and
level(?level);
saleTrader(?sales);
orderTrader(?order);
}
calcSuppyAndNewLevel(?order,?level,?Sales,?newLevel,?newSupply);
Consequents:
and
level(?newLevel);
supply(?newSupply);
3) Rules
in the agent type Distributor (distributors are sub-agents of the agent Model)
3.1) Rule for distributors’ demand and
order-setting
This rule is written at each Distributor.
It is valid for any iteration (e.g., it is applied) recursively. Notice that
the agent (Distributor) and
the iteration are implicitly referenced.
Antecedents:
and
lastIteration
{and
demand(?oldDemand);
sale(?trader,self,?oldSale);
saleDistributor(?oldSaleDistributor);
listSelTrader([?traderSelected ?other1
?other2]);
order(self,?trader,?oldOrder)
}
calcNewOrder(?trader,?traderSelected,?oldDemand,?oldSale,?oldOrder,
?oldSaleDistributor,?newOrder, ?newDemand);
Consequents:
and
demand(?newDemand);
at Model write:
order(self,?trader,?newOrder);
}
{if the agent
and the iteration were explicitly referenced, the rule would be (after the
appropriate changes in the definitions of the predicates):
Antecedents:
and
demand(?distributor,?oldDemand,?i);
sale(?trader,?distributor,?oldSale);
saleDistributor(?distributor,?oldSaleDistributor);
listSelTrader([?traderSelected,?other1,?other2]);
order(?distributor,?trader,?oldOrder)
calcNewOrder(?trader,?traderSelected,?oldDemand,?oldSale,?oldOrder,
?oldSaleDistributor,?newOrder, ?newDemand);
Consequents:
and
demand(?distributor,?newDemand,?i+1);
order(?distributor,?trader,?newOrder,?i+1);
}
The first exploration of the simulation trajectories
was performed at the MAS level using a model built in SDML. This stage of
observation corresponds to what in Chapter 6 is proposed as the first level in
a hierarchy of architectural transformations. A sort of scenario analysis was
made generating several simulation trajectories.
These trajectories corresponded to different
values of parameters of the model and agents’ choices. Parameters of the model
were, for example, the capacity of the warehouse and the rate of supply from a
trader to a distributor. The non-deterministic choice modelled was the trader’s
price-setting. Traders imitate other traders’ prices. For this purpose, each
trader chooses another trader each day. This was implemented using the
predicate listChoiceTrader(Trader,
Trader,Trader, i). At this stage of the experimentation, only one
alternative for trader’s choices is allowed per iteration and a single
trajectory is explored per run. If all alternatives for choices were allowed in
the model, as the total number of traders is three, each of them would have two
choices, and there would be a total of 2 x 2 x 2 = 8 alternative price-settings at each iteration.
The alternative choices for price-setting (traders’ choices of another trader)
at day i were:
Choice 1: listChoiceTrader(Trader-2,
Trader-1, Trader-1, i);
Choice 2: listChoiceTrader(Trader-2,
Trader-1, Trader-2, i);
Choice 3: listChoiceTrader(Trader-2,
Trader-3, Trader-1, i);
Choice 4: listChoiceTrader(Trader-2,
Trader-3, Trader-2, i);
Choice 5: listChoiceTrader(Trader-3,
Trader-1, Trader-1, i);
Choice 6: listChoiceTrader(Trader-3,
Trader-1, Trader-2, i);
Choice 7: listChoiceTrader(Trader-3,
Trader-3, Trader-1, i);
Choice 8: listChoiceTrader(Trader-3,
Trader-3, Trader-2, i);
where the trader in position i is the choice for Trader-i.
For instance, in case of the fourth choice (Choice 4: listChoiceTrader(Trader-2, Trader-3, Trader-2, i)), Trader-1 chooses Trader-2, Trader-2
chooses Trader-3 ,and Trader-3 chooses Trader 2.
A tendency was ‘discovered’ when examining the results of
the simulation: the range of traders’
prices stabilise over time and its size decreases monotonically over time. This
tendency was common to all generated trajectories. Trajectories were explored
for 20 or 30 iterations. Now that a tendency has been found, the idea is to
investigate it better. The following step is to examine the commonality of the
tendency in different trajectories and, if possible, to prove it.
In a trajectory, there are three agents of interest
for the analysed tendency (the traders). Each agent has its individual
trajectory in each simulation trajectory, as was graphically represented in the
left side of Figure
5.2 for the case of two agents. Along each trader’s
trajectory there is a trajectory of the variable prices: that trader’s
product’s price (a typical example of the three price trajectories for a single
simulation trajectory is shown in Figure
7.3). These three outputs are obviously
interrelated. The idea is to study them
either by enveloping them as shown in the lower part of Figure 5.3, e.g., by generating a single envelope for the whole
subspace of the relevant simulation outputs (the tendency about prices)
obtained from the exploration of all simulation trajectories; or, by enveloping
them for each simulation trajectory and then examining all envelopes generated
for all explored simulation trajectories, as will be the case in this
particular application.
In the case relevant in the present study, there are three
price trajectories resuming the aspects of interest for each simulation
trajectory. Each sample of these price trajectories a simulation trajectory
gives is the result of the interplay of agents’ choices for a single
parameter-setting during a finite number of time iterations. The idea is to
envelope these three price trajectories and to study them better, not only for
a single simulation trajectory but for a subspace of them - that defined by
range of parameters, agents’ choices, and a finite number of time interations.
The specified output of interest,
traders’ prices, was then enveloped in accordance with the discussion in
section 5.3. This is the case of a one-dimensional output and it
is of interest to envelope the observed tendency, Y, using two value
sets Eupper and Elower for each simulation trajectory, as
was explained in section 5.3 for the discrete case.
In accordance with this, per each iteration in a simulation
trajectory traders’ prices might be delimited, e.g, by the highest and the
lowest traders’ price for that iteration. (i.e., the envelope value set at t
is defined by the interval: [highest traders’ price at time t, lowest
traders’ price at time t] = [Eupper|t , Elower|t
]). As was stated above, in this case, it is of interest to generate an
envelope of the tendency for each simulation trajectory. Should the tendency be
enveloped for all explored simulation trajectories, again the tendency would be
given by the worst cases; i.e., its bounds for time iteration t would be
given by the union of all intervals obtained for t (one for each
simulation trajectory).
E.g., if we knew traders’ prices for two days in a
trajectory:
- for day 1: 0.40, 0.45, 0.43, and,
- for day 2: 0.42, 0.43, 0.41;
then the output of interest, i.e.,
the enveloping set of values for this trajectory, would be:
- for day 1: 0.40 and 0.45;
- for day 2: 0.41 and 0.43.
The relevant property of the tendency is a measure of this
envelope, so that, for day t, what is of concern is the difference
between the maximun and minimun prices on that day. Remember that the tendency
identified in the previous section was that the amplitude of the interval for
prices is decreasing over time. For the example, this output would be:
- for day 1: 0.05;
- for day 2: 0.02.
The values of this measure for a typical simulation
trajectory are presented graphically along the trader’s prices as the lowest
curve in Figure
7.3.
Therefore, the interest in this case is not in studying a
common envelope of the tendency for all simulation trajectories, but in
analysing envelopes for each simulation trajectory. The concern is to prove
that a property of the envelope of the tendency in a simulation trajectory holds for all instances of the
envelope in all explored simulation trajectories, rather than (what is an
alternative) to prove a property of a single envelope covering all instances of
an output for all explored simulation trajectories.
In order better to explore the simulation dynamics
and the possibility of proving tendencies in a subset of the trajectories, the
model is translated into the theorem-prover OTTER. This seems to be isomorphic
(discussed in section 5.10.1), since each instance of data and rule in the
original SDML model had an equivalent instance in OTTER. Obviously, the
implementation, though equivalent, has differences, as OTTER gives different
facilities and other levels of programming. In OTTER, it is necessary to
express all data and all rules in a single DB-RB pair, as OTTER does not offer
either the hierarchy of agents or the hierarchy of time levels.
Hence, SDML’s hierarchy of DB-RBs
becomes a single database–rulebase in OTTER. Because of this, information
implicit in SDML has to be made explicit in OTTER. For example, predicates in
OTTER have to be modified in order to add data about agents and time levels
given implicitly in SDML. For instance, predicate Price(Value) at agent ‘Trader-1’
has to be written in OTTER as Price(Trader-1,10,
iteration). That is, agents, objects, and time
iterations have to be explicitly specified in predicates.
The main characteristics of the
procedures used in OTTER for proving have been described in Chapter 3. OTTER is
clausal-ordered (syntactic) and forward-chaining. It uses the set of support
strategies. The old version of OTTER allows a user to implement only implicit
split, but the newer UNIX versions also permit a modeller to implement explicit
split (see Chapter 3). Most of the experiments were made in traditional OTTER
using implicit split but as soon as the option for explicit split became
available, it was also used.
In fact, implicit split has to be
somewhat user-driven; the user himself has to program the search and
exploration of the different simulation branches generated by the agent’s
choices. This can be implemented by adding a field into the predicate for
identifying simulation branches. Different branches generated at a choice point
are identified with a different assumption label – also user-handled. The idea
is that different instances of data in a branch share the same assumption. In
the model, each trader’s choice was identified with a different number (from 1
to 8). For example, the predicate:
sale(‘Trader-1’,
‘Distributor-2’, 10, 6, [1 5 3 8 2]);
indicates
that ‘Trader-1’ has sold 10 units of good to ‘Distributor-2’ at time interation
6 in the simulation trajectory correspondng to assumptions [1 5 3 8 2], i.e.,
agents have made choices 1, 5, 3, 8, and 2 on days 1 to 5 respectively.
The model in OTTER resulted from
translation of the original simulation model built in SDML that seems to be
isomorphic (see Chapter 5). Inference is applied using a single set of clauses,
placed in the support set (this is part of the programming strategy in OTTER;
see Chapter 4). While OTTER’s inference mechanism is clausal, the
implementation in SDML is logical model-oriented. Rules in SDML were rewritten
in OTTER as clauses in the support set and then hyperresolution was used as the
inference mechanism. Forward-chaining was applied over data in a path that
advanced over the simulation time. This mechanism also propagates assumptions.
New branches are generated as alternative results of a resolution (e.g., a set
of resolvents, rather than a unique resolvent, results from applying
hyperresolution to a set of clauses). The inference mechanism is then
forward-chaining, driven by the support set and hyperresolution.
The proof procedure implemented
in this model in OTTER has similarities to that followed in tableaux in the
sense that the negation of the theorem (tendency) to be proved is added. A
simulation path is closed as soon as a contradiction appears. This happens when
the tendency turns up in the path. If all possible paths are closed, then the
tendency is proved. On the other hand, if at least one path remains open and no
more data can be generated, the proof fails – the open path providing the
counter-example to the tendency. How the simulation paths are generated (for
the parameters of the model and choices of the agents) is illustrated in Figure 5.2 of Chapter 5.
As soon as the proof is
attempted, its complexity becomes evident. The number of simulation paths
increases tremendously with the number of iterations allowed in a trajectory. A
huge amount of computational resources is required. This become clear
considering the number of simulation paths to be investigated as a function of
the number of days, remembering that there are eight alternative choices (the
traders’ choices) at each branch each day. For instance, if the simulation is
carried out for 2, … , 10 simulation days, there will be: 8, 64, 512, 4096,
32768, 262144, 2097152, 16 777 216, 134 217 728, 1073741824 paths. The
experiments were made in a PC with 256 MB RAM, which was able to simulate for
up to 6 iterations and 32768 simulation paths (85 simulation step
transitions).
At this stage it becomes clear
that this sort of proof has to be restricted. Clearly, the principal
constraints are the limited computational resources and the number of
iterations. More generally, constraints have the following sources (at least in
the simulation of social systems):
·
Technical
o
Limited
Computational Resources given by a PC and its 512MB of RAM
o Manipulation of real numbers: the presence
of real numbers makes it difficult to evaluate the similarity of paths and
prune the search. Conditions assuring a similar behaviour of prices can be
found, but it is very unlikely that these similar conditions repeat during a
simulation, as they will be given in terms of floating point numbers (basically
in terms of prices and sales, because the instances are driven by the traders’
price-setting). If the intention had been to prune branches, information about
all particular conditions found while the simulation was going on would have
had to be kept in order to compare them with new conditions found, which is
expensive in terms of memory and time. Moreover, it is not easy to manipulate a
database in theorem-provers like OTTER (see Chapter 5). In fact, it would have
been necessary to add special facilities into OTTER’s code and to recompile it.
Thus, this alternative would result in relatively little advantage even when
compared to high-level languages such as those for programming MAS.
·
Complexity of modelled systems
o Unforeseen
(especially qualitative) changes in ‘empirical systems’. Qualitative changes
are generally present in MAS applications as, for example, agents can be
introduced and eliminated. Nonetheless, they were not present in the
experimental model.
The first models in OTTER using implicit
split were built in 1998. Additional versions of the model in OTTER using
explicit split were built at the end of 1999. When using explicit split, at
each choice point OTTER saves the state of the system in order to backtrack and
explore alternative choices. Once a path is followed successfully, OTTER
reports the relevant details about the result in that branch and backtracks
until the latest choice point in order to follow another path.
SDML’s characteristics and facilities, and SDML’s
inference mechanism for proving theorems in the theory of a simulation model,
were discussed in sections 5.9.1 and 5.9.2. Most of those facilities were present at the moment
of implementing the model discussed in this chapter. The only new one added
was:
·
A simple negative contradiction generation via false
predicate: P => ⊥
This new facility was conceived by Bruce Edmonds and
aggregated into SDML by Steve Wallis.
The idea at this point was to build a new model in
SDML. The new model consisted of a single DB-RB pair for facilitating reasoning
about the whole simulation model. The primary reason for having a single DB-RB
pair is because SDML does allow backtracking over time levels or between agents
(a side effect of this was the huge number of assumptions generated). The plan
is to experiment in SDML with a similar model to that built in OTTER and, in a
following step, to improve the efficiency of this new model. The main aspects
of this first translation are shown in section 5.9.3.1, which, as will be seen in section 7.8, turns out to
have some serious drawbacks; then, in section 7.9, a more efficient
implementation will be discussed.
A difficulty appears after revealing dependencies:
the space of data matching the antecedent of the transition rules grows
linearly with the number of iterations. However, most of these attempts are
redundant, in which case no additional data is generated by the rule. These
redundant rule-firings slowed down the simulation. These drawbacks are
discussed in section 0. In order to deal with these drawbacks, the rules
will be ‘unwrapped’.
The next step is to unwrap the rules. To write rules
for iteration i+1 referencing
explicitly data at iteration i,
it would be necessary to know such data previously. That is possible, for
example, if, at the beginning of the simulation, the names of the predicates
alluding to the data to be instantiated are known and if the language permits
one to write the rules using those predicates. This is possible in SDML using a
meta agent. Another way of splitting rules would be by writing them even more
dynamically while the simulation is going on, e.g., writing the rules for iteration i+1 once the data for iteration i is known. This option is not available in
SDML when using backtracking. When using backtracking, a meta agent acts
in advance of the agent it is writing to. So, the information the meta
agent uses has to be given in advance of the target agent’s activation (e.g.,
in this case during the initialisation of the simulation).
The idea, then, is to ‘declare’
(give explicitly in the model) as much as possible of the semantics of the model.
The intention is to declare all instances of agents and objects in order to
make possible the identification (in the program) of the range of agents’
choices and model’s parameters, and to declare the names of predicates
referencing data so that this information can be used dynamically by transition
rules in advance of the activation of the meta agent (a meta agent operates in
this application as a module and will be called meta). The module model
is responsible for setting these initial conditions in the
simulation. An overview of the efficient model built in SDML is given in Figure 5.18.
Afterwards, meta uses this semantic information in
order to write a set of transition rules for each iteration, making the
information to be instantiated by each rule as explicit as possible and
eliminating the problem described above. Figure
7.2 pictures the whole translation process from the
original MAS-based model in SDML to the efficient (logical) model
constraint-based implementation (it is constraint-based because the
trajectories are generated for a (complete) range of parameters and choices).
Trajectories in the four models,
the two models implemented in OTTER, the first MAS-based model, and this new
(efficient) implementation seem to be equivalent, since they generate the same
instances of data for a single iteration. That is, the models appear to be
isomorphic to each other under the experimental frames defined by the data
a modeller wants to observe (namely price-setting, order-setting, and
price-imitating) and the range of parameters and choices taken, in the strict
sense defined by Zeigler (this is discussed in section 5.10).
|
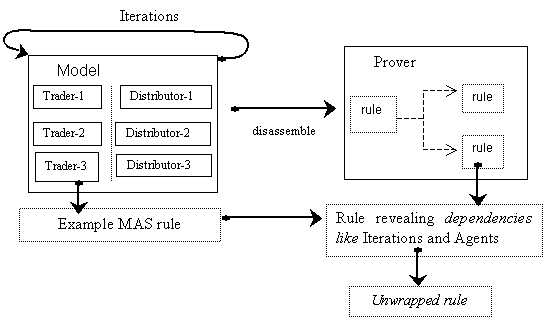
|
|
Figure 7.2.The whole procedure of revealing dependencies and
unwrapping rules
|
The translation process of a MAS-based model into a
constraint-based architecture that might be implemented automatically would be:
1. Identify
MAS constructs hiding rule dependencies (e.g., time levels, agents, or
objects). Look for ‘general’ descriptions of the dependencies. E.g., a trader's
price at iteration i+1 depends
on traders' sales and prices at iteration i.
2. Redefine
predicates by adding fields (e.g., for time levels and for agents) in order to
make the hidden dependencies explicit. In order to do this, it is necessary to
define predicate-types more specifically; e.g., rather than declaring only the
predicate price, the idea is to declare, for example, price1,
price2, .., representing price at iteration 1, 2, …. - the
hidden rule dependency iteration is revealed. This is useful for
referencing instances of price more specifically.
3. To
facilitate reference to data when writing meta-rules in 4, it is useful to
create a list of references or links to instances of predicates involved in
these new dependencies. This is given by the predicate’s names. Taking the
example of the rule for prices, lists containing the names of the predicates
for prices and sales are created (e.g, lists like [Price1, Price2 …, Pricen] and [Sale1, Sale2, …, Salen]).
Lists containing objects’ and agents’ names might also be specified.
4. Initialise
the simulation. This includes the range of parameters and choices, and the
state of the simulation at iteration 1.
It is a task of module model (see above). It creates data to be used by meta in order to write the transition
rules for iteration 2.
5. Using
these settings and knowledge about rule dependencies, meta-rules are written at
meta which are responsible for writing (at the module prover)
the transition rules (referencing as explicitly as possible with respect to the
data), which are, in turn, responsible for executing the proof.
The original model was useful for generating single
trajectories. There a scenario analysis can be accomplished but the user has to
execute and observe each trajectory individually. As was said above, the
advantage of the MAS architecture is the high level of programming. It allows
the modeller a good understanding of individual trajectories, as a lot of
information about the quantitative and qualitative evolution of the simulation,
both written and graphical, can be generated.
On the other hand, using the
constraint-based architecture, a restricted proof of the tendency was achieved.
All trajectories were generated for a combination of parameters and all
traders’ non-deterministic choices over six simulation time iterations.
In principle, there were eight
‘types’ of rules (see Table
12.1) in the original model involved in the application of
the technique: those associated with generating the dynamics of the simulation
(namely the transition rules, of which there are seven), the rule for checking
the theorem, and the rules for setting up the traders’ choices. The last two
did not suffer additional split. The seven transition rules were split into 85 rules
in the new model. Each of them was split by iteration, and two suffered
additional split by trader. Distributor also split one of these rules. This
gives: (5 + (1 + (1 * 3)) * 3) * 5 = 85 rules in the logical model
constraint-based SDML model, replacing those seven named rules in the MAS model.
For more details about the sets of rules in the two models, see Appendix 5.
Other facts
about the case study are:
• With the
computational resources available at the moment, the efficient constraint-based program executed the
proof in twelve hours, while the original one needed seven days.
• There were 85
= 32768 explored paths in the (logical) model constraint-based model.
This section intends to make clearer
the interrelationship among the concepts of explanation, understanding, proof,
and changes in a modeller’s internal model, discussed in section 5.6 (more precisely, see Figure 5.4), by using the experience of discovering and proving
an emergent tendency in a simulation presented in the previous sections.
As was said in section 5.6, to
understand a tendency a modeller would have to find meaning for it by himself
(i.e., in his internal model); he has to bring about his own explanations or
insights about how the tendency arises.
As mentioned in section 5.6, changes in the modeller’s cognitive model might be
either light, like those additional details a particular simulation trajectory
can produce, or stronger, such as those created by new insights that a new
simulation approach, a new paradigm in science, or the process of giving
meaning to an emergent tendency can create. For example, as was discussed in
Chapter 4, if a subject finds an explanation for an emergent tendency, then a
new language might appear in the subject’s cognitive model. This might bring to
the subject not only new explanations for related phenomena but also new ways
of approaching them, new insights, and probably a new world view in different
matters. A new language in a subject’s cognitive model might work like a new
paradigm in science.
In the MAS-based model single
trajectories can be observed. At this level, it was noticed that traders’
prices became closer over time and practically similar after a certain number
of iterations. This finding was helped by appropriately presenting the
information graphically (see Figure
7.3). This fact, observed in single isolated
trajectories, has two important components: those outputs about which
hypothesis is arising, i.e., traders’ prices; and a property the hypothesis is
referring to, i.e., that one given by the differences among prices, or,
equivalently by the size of the interval defined by the smaller and the higher
prices per day. The hypothesis is that such an interval decreases over time.
Why this tendency arises is not clear. A causal ‘explanation’ in terms of the
computational model would be given by the sequence of transition steps the MAS
carries out for generating this tendency. However, this is not an explanation
for a modeller and it is a fact concerning only a very tiny part of the
simulation model theory (that a single trajectory offers).
At this point the tendency could
be considered emergent since it has not been understood by the modeller; the
modeller has neither and explanation nor an insight to give it sense. On the
other hand, as the tendency has been observed only in isolated simulation
trajectories, no conclusion with reference to the simulation theory can be
drawn.
Further investigation of this
tendency is made by implementing a constraint-based exploration of all
simulation trajectories in a subspace of the simulation theory. This space is
supposed to be relevant in accordance witht the modeller’s goal, e.g.,
including those parameter-settings that seem more likely to happen in the
empirical system or those involving what the modeller believes to be the most
significant ones because of a certain critical value of some output.
Using the logical model-based
constraint architecture, a restricted proof of the tendency was achieved for a
single parameter-setting, all agents’ choices, and six time iterations. This
involved the exploration of 32 678 simulation trajectories. As the tendency was
observed in all explored simulation trajectories, it informed the modeller that
the tendency was a fact in that fragment of the theory given by the simulation
model constraint under that single parameters’ setting, all agents’ choices and
six time iterations. This result gives a more general conclusion than that
offered by the MAS-based model.
A drawback of this procedure
might be that, as more data is involved (that of the 32 678 explored
trajectories), it is likely to make it more difficult for a modeller to find
his own explanation and to understand the tendency. On the other hand, however,
such an exploration of a whole fragment of the simulation theory might allow
the modeller to elaborate theoretically valid conclusions, to bring in new
insights for some analytical theory, and afterwards probably to update some of
his own basic beliefs and intuitions. In this case, it would bring more
essential knowledge than the MAS-based model, as more basic aspects of the
modeller’s cognitive model would be changed.
Likewise, proofs at an even lower
level of programming would give even less detail about single trajectories, but
they might offer a modeller stronger conclusions about the theory in the
simulation model and bring more fundamental changes in his knowledge (more
likely, they would generate structural change in his cognitive model) than
those the model-based constraint architecture offers. Nevertheless, it is
likely that the former architecture would be less useful than the later one in
helping a modeller to understand in a trajectory particular details associated
to an emergent tendency.
The more involved the modeller is
with a model and the better validated he feels the model is, the more likely it
will be that simulation results from these architectures of programming modify
the modeller’s understanding about the empirical system. In addition, several
characterisations of the simulation results via constraint-based proofs of
tendencies will allow a modeller to characterise a range of behaviour in the
model via a set of relations involving the range of parameters and choices on
the one hand and the envelopes of the simulation outputs on the other; i.e., he
will collect sets of envelopes of the simulation outputs for different
fragments of the theory. All this will assist in training the modeller about
what to expect from the empirical system. Such training will inform the
modeller and change his expectations about details related to how events unfold
(by observing single trajectories) as well as about more general and deeper
issues (that the constraint-based architecture offers).
The idea of this section is to
briefly contrast the constraint-based approach exhibited above with other
procedures used for similar purposes, namely to explore the dynamics of
simulations, to prove theorems, or, in general, to investigate tendencies in
the theory given by a computational program. That is, the aim is to explore the
consequences (the dynamics) of computational programs so that a modeller might
improve his understanding of aspects of the program itself or/and of an
empirical system modelled. Some of these computational programs were reviewed
in Chapters 2 and 3. In particular, the interest is in those computational
tools related to this thesis: either using a declarative approach for agent
simulation or with a potential for theorem-proving. This will include: the theorem-prover
OTTER, the experience of people working with DESIRE (Engelfriet, 1998), and the declarative system METATEM (Fisher, 1996).
OTTER is a theorem-prover (see Chapter 4) using
clause-ordering (weighting) and a support set for efficiency. In SDML, the
criterion for firing rules is well understood, and procedures like weighting
and subsumption used in theorem-provers such as OTTER are not usually needed.
In SDML the main source of efficiency is the exploitation of rule dependences.
Information about predicates and their temporal order is exploited in SDML
using an automatic mechanism for the static analysis of dependences (see
Chapter 5 and Moss et al.,1998a).
Among other approaches for the
practical proof of MAS properties, the more pertinent appears to be the case
conducted by people working in the DESIRE project. They proposed a hierarchical
verification of MAS properties, and succeeded in doing this for a system
(Engelfriet, 1998). The first part of the proof consists in proving that agents
at the lower level of the hierarchy (those not containing sub-agents) satisfy
the goals they are supposed to achieve. That is, for each type of agent at the
lower level, it is proved that its goal is a theorem of the theory given by the
rulebase of the agent. Then properties about agents at the next, higher level
up (i.e., those whose sub-agents are all in the lowest level) are proved. Their
properties depend on their own rulebase, and on their sub-agents’ rulebases and
properties. This procedure is continued until proving that the whole system
(the agent at the highest level) has the correct behaviour.
The DESIRE group’s aim is the verification of
properties of a computational program, by proving that the program behaves in
the intended way. Proofs are about aspects that are supposed to be introduced
in the structure of the simulation model rather than about ‘new’ features
observed in the dynamics of the simulation.
Satchmo’s and other constraint
programming systems offer facilities similar to those of SDML, for example, backtracking
and the false predicate. However, they also have built-in facilities for
the manipulation of constraints, something SDML lacks. Instead, SDML presents
facilities to introduce alternative values for the manipulated entities (e.g.,
predicates, clauses, integer variables), which can be used as constraints
(clauses for choosing, e.g., randomChoice) as well as a meta module able
to reason about terms or rules. As was seen above, a meta module can
build rules to take advantage of the simulation semantics. A meta module
able to act while the simulation is going on could adapt the search to the
simulation results. Though SDML’s approach is different from constraint logic-programming
languages, it is able to control the manipulation of constraints flexibly and
transparently for the user via the mechanisms described.
It should be possible to
re-implement the example model in some of these systems, for instance in CHRv.
This is an area of further research that will help in developing an even more
appropriate methodological approach for proving in MAS.
MetateM and concurrent MetateM are
languages implementing executable temporal logics. They are in the family of
languages following the imperative future paradigm (past and present → (implies)
future) (Barringer et al., 1991;
Fisher et al., 1995; Fisher, 1996).
Consequently, their execution mechanisms seem to have many similarities with
SDML’s and, in general, with forward-chaining oriented languages. Nevertheless,
there are several differences between MetateM and SDML. These are related to,
on the one hand, the way agents and their interactions are conceived, and, on
the other hand, their capabilities for exploring and proving tendencies about
the dynamics of a simulation.
In MetateM the order of the rules depends on a temporal
order of eventualities; the rule with the oldest outstanding eventualities is
chosen as the rule to be executed (this is explained in Fisher (1996), p. 2,
section 2.2, in the Postscript version of the paper). It depends dynamically on
both the rulebase and the database. Instead, SDML’s rule dependencies
management is static - rule dependencies do not change over time. This implies
both advantages and disadvantages.
A disadvantage for MetateM seems
to be the difficulties for tracking those eventualities, as it implies a
dynamic modification of certain links to the database. This must be both time-
and memory-consuming. In some sense this presents similarities to event-driven
simulation, where a future event list determines at each time the next
transition states to be generated. Nevertheless, in event-driven simulation
each type of event as well as its consequences over the state of the system are
assumed to be well known in advance. Eventuality-driven rule-firing might be
difficult if the dynamics of the ‘eventualities’ are not well known. This sort
of exploration suggests a sort of time-driven simulation, still not flexible
enough for implementing efficient theorem-proving mechanisms (a single and
fixed criterion is driven the search at a meta-level).
MetateM allows backtracking and
branch exploration in agent database in case no data have been sent to other
agents or to the environment. This sounds inflexible and inconvenient for
theorem-proving. SDML has a similar inflexibility when using backtracking where
several agents (and thus several databases) are used. This is one of the
reasons a single DB-RB pair has been proposed for a constraint-based exploration
of simulation trajectories. In fact, if backtracking of the simulation in a
population of agents were allowed even after messages have been transferred
among agents, then ideas would have to be brought from parallel simulation and
distributed programming to maintain the feasibility of the computation. The
difficulties for backtracking when using concurrent processors or parallel
databases (the usual case in a MAS) obviously vanish once the model is
translated into a single DB-RB pair.
Transference and access to
messages is controlled in SDML by using the hierarchy of agents, data
attributes, and by writing data to other agents; e.g., one attribute of an
agent’s predicates can be either public (accessible to any other agent) or
private (accessible only by the agent itself and by its container). This is
less flexible in MetateM as there it is tied to other aspects of the model. In
MetateM, it is necessary explicitly to specify in the definition of an agent
which types of data this agent can accept as input, and which types of data
this agent can send to other agents.
Though METATEM is appropriate to
implement agent simulation and theorem-proving, facilities might be added or
existing ones improved (e.g., for allowing backtracking even after agents have
interchanged messages) to make it even more suitable (this is also the case
with SDML).
The aim of this chapter is to discuss some of
the implications of this thesis in related areas of research, such as:
complex systems, social simulation, MAS, policy analysis, and
logic-programming.
First and as a preview, in section 8.2, conditions of how
this thesis works in relation to other methods will be discussed. The idea is
to situate better the results obtained in this thesis with respect to other
research areas and their methods as well as to discuss the feasibility of the
proposed methodology and techniques in other areas of research and with respect
to the computation techniques available at the moment. This will also involve
discussions about the trade-off between the complexity of the proposed
methodology and techniques and its usefulness for studying complex systems.
Second, in section 8.3, advantages of a hierarchy of
architectural transformations (such as that proposed in Chapter 7 for dealing
with the difficulties behind modelling complex systems) will be
discussed. In addition, the benefits of using a language permitting changes in
the structure of the (simulation) model at the level of the rulebase and at the
level of the components (e.g., allowing introduction and destruction of agents)
will be discussed.
Then, in section 8.4, benefits of a hierarchy of
architectural transformations (e.g., that given in Chapter 6) and of a more
specific notion of emergence of tendencies (like that presented in Chapter 4)
for the social simulation community will be considered.
Afterwards, in section 8.5, advantages of using hierarchies
of architectures rather than a single one (the MAS itself) for different MAS
communities in accordance with their needs and goals are discussed. Work in
this area can already be found in the MAS literature, though generally those
hierarchies are not intended for exploring tendencies in a simulation. Usually
they are aimed at facilitating a MAS implementation; different architectures
allow a programmer to specify a MAS at different levels of programming.
The next section (8.6) is aimed at recapitulating how the conception
of emergence has been elaborated in this thesis, underlining its usefulness
for decreasing controversy in areas of research such as social simulation. The
relevant aspects of the research stances from which this conception originated
are brought in.
In section 8.7, the importance of a hierarchy of
architectures as an informative and ‘educative’ tool for studying soft
systems, and in particular for policy analysis and management (where
the subject studying the simulation is usually situated in the target system),
is considered.
Finally, in section 8.8, the convergence of, on the one
hand, communities of modellers working on MAS-based applications (e.g.,
MAS-based social simulation) progressing towards architectures allowing proofs
and, on the other hand, communities working on logic-programming starting to
use the more flexible programming tools of constraint logic-programming, will
be discussed.
The particular technique was developed for SDML, but
the methodology could be adapted to other simulation platforms. The idea is to
allow, in the corresponding platform, the implementation of a proving procedure
by adding facilities (e.g., for assumptions management, splitting,
backtracking, context-reasoning) and of how to rewrite the (possibly MAS-based
or event-driven) simulation procedure in a single DB-RB pair in order to
facilitate reasoning and to overcome particular limitations due to abstractions
(like agents and time level hierarchies in SDML) that the particular platform
presents. The general idea then would be, first, to reveal and, second, to
exploit some of the language abstractions and facilities in order to build a
proving procedure. The ideal step would consist in allowing automatic
translation of simulation models from the original architecture into the
proving architecture.
Implementation of a platform for automatically
translating MAS-based models into constraint-based models seems difficult at
present, at least for ‘sufficiently’ rich models (e.g., those with many agents
which are continuously eliminated and introduced in the simulation). A wider
application of the methodology proposed in Chapter 5 would require computational procedures allowing
simulation of the weak structural change that MAS-based platforms permit, e.g.,
introduction and elimination of agents.
That such difficulties exist is guessed because of the
struggles in other areas of research where similar computational techniques are
needed (e.g., in parallel simulation). In addition, theorem-provers are not
flexible about modifying the structure of the model, so that it would not be
possible to drive hints from this area of research.
To implement a constraint exploration of a simulation in
rich models will involve dynamical manipulation of the rulebase and database
from a meta-level. To do so, the database has to be appropriately designed in
order to facilitate distinction among data associated with those entities whose
structure can change or with entities that can be introduced in and eliminated
from the simulation. The complexity of this computational work, plus that of
the exploration the proof procedure requires (discussed in Appendix 6), would
benefit from introducing parallel computational techniques, as these
facilitates complex tasks by distributing computational sub-tasks among several
processors. Nevertheless, parallel simulation is an area of research still
struggling to develope appropriate computational techniques (see, for example, Nicol et
al., 1994). In conclusion, there are sufficient techniques
difficulties in the way of creating a platform making possible constraint-based
proofs of theorems, that we may guess it will take some time before an
implementation accessible to modellers will be put into practice.
With reference to the complexity of the search shown
in Appendix 6, the most critical factor for the high complexity of the search
is the number and frequency of the processes’ choices. If this frequency is low
(e.g., null for some time iterations), then the complexity of the exploration
this thesis proposes would not be too high, as happened in the case presented
in Chapter 7. This is the case in many simulation applications
where the complexity is rooted in the simulation process rather than in the
number of choices. For example, in the case study presented in Chapter 7, traders’ price-setting might be based on a more
complex cognitive model by taking into account and modelling additional factors
of their environment, as is the case in existing models commonly used in
organisational and social simulation (see for example, Moss, 1998; Carley et al., 1998; Edmonds, 1999c). It will
make an agent’s decision more subtle but also more deterministic. In the other
extreme case, if processes’ choices are frequent, as in the case presented in
Chapter 7, then the complexity of the search will be high and
it will be costly to implement the proposed model constraint-based exploration.
In such a case, a more syntactic approach might reduce the computational
complexity of the search in terms of time and memory needed. In addition, to
allow alternative settings for the environment (environment’s choices) will
increase the complexity of the exploration, though the analysis of such
complexity can be made using the study presented in Appendix 6 (e.g.,
environment’s choices could be placed together with agents’ choices in the ‘or’
nodes of Figure
15.1).
Usually, robots are situated in environments where
they are supposed to interact physically among themselves and with their
environment (examples of such applications can be seen at: http://www-poleia.lip6.fr/~drogoul/).
They not only have capabilities for communicating via message-passing where
physical interaction is abstracted and performed ‘symbolically’ (as
trader-distributor interaction has been abstracted in the example of Chapter
7), but they also have capabilities for physical interaction; e.g., they might
be able to move, to perceive noise and sound, to visualise, and to send sounds.
In addition to other agents’ behaviour, the events occurring in and the
structure of its physical surroundings are relevant for an agent’s cognition.
Possibly the complexity of the simulation model would be
subtle, but this subtleness would be more due to the structure of the model
than to the agent’s choices. Consequently, there will hopefully not exist a
high frequency of agent’s choices and the complexity of a constraint-based
exploration will not be too critical (see Appendix 6).
In the ALife project and in Microsimulation
applications (see, e.g., Langton, 1989; Nagel et al., 2000), simpler agents are modelled than those considered in
social simulation. They are simpler agents in the sense that their cognitive
model does not generally correspond with elaborated theories of cognition.
While in social simulation, evolution of both the agent’s cognition and the
model’s structure are important phenomena, usually in models used in ALife and
in Microsimulation the main interest is in the evolution of the agents and
their interaction. The complexity in the experimentation is deeply rooted in
the number of agents and their interactions rather than in the evolution of
agents’ cognitive models. Generation of the dynamics of the model commonly
involves the introduction and elimination of agents in very dynamic
populations. Consequently, even a few choices for each agent would make a
constraint-based proving procedure difficult because of the large amount of
branch points to appear (there are many agents), making the usefulness of the
technique limited.
At present, some event-driven simulation languages
allow some sort of structural change, e.g., limitedly in SLAM (see Pritsker,
1995) and, as has been shown in Terán (1995), more broadly in GLIDER. Allowed
changes include elimination and introduction of elements of the structure of
the model. For example, in Terán (1995), the exploration of several structural
paths was executed in a single simulation. There, the alternative structures
and conditions for the structural change to happen are predefined at the
beginning of the simulation. In this sense the change is somewhat fixed in
advance. This restricts ‘creativeness’ and other context-reasoning
capabilities. In a rich environment this might be a very strong and even
obstructive constraint. In addition, as these languages are procedural, it is
not easy ‘to evolve’ agents’ function (this is different in a declarative
language like SDML). These are limitations for implementing context-sensitive
changes in the agents’ and model’s structures and for constraint-based
exploration of trajectories (either logical model or syntactic-based).
This thesis attempts to find a more practical notion
of emergence (considering subjective aspects) than those objectivist ideas
traditionally used in science, e.g., in physics and in computational modelling.
The idea is not to dispute the usefulness of the objectivistic conceptions, but
to suggest alternative approaches more likely to be supportive in some
modelling applications.
But, why is a subjectivist notion likely to be more
practical in some cases? Consider a typical example where an objective notion
of emergence is typically used: emergence of life on earth. Emergence of life
is usually ‘objectively’ described as dependent on the object itself as, e.g.,
the result of chemical reactions. This seems a good approach as far as it works
satisfactorily for the modelling goals. However, there are research areas such
as those involved in studying social systems where good ‘objective’
approximations to key notions are missing – probably because of the high level
of complexity of these systems - and more practical definitions would be
valuable. An example is the notion of emergence of tendencies in social
simulation.
In these cases, it seems that sometimes after a modeller
adopts a simulation and modelling methodology, his subjective judgment of the
simulation results and of the dynamics of the empirical system plays an
important role in making theory.
Because of this, in the view of the present writer, it is important to
uncover the subjective factors involved in studying simulation models, e.g.,
for studying emergent tendencies in social and organisational simulation. In
addition, a formalisation of these ideas would help in explaining what happens
in an agent cognitive model (see, e.g., section 4.5.2) when ‘understanding’ its environment.
This idea is not new and the distinction of subjective
factors in the modelling process can be found in the simulation and modelling
literature, for instance, in Zeigler’s definition of experimental frame and his
differentiation between real system, base model, and lumped model (Zeigler,
1976), and in Crutchfield’s examining of subjective and objective factors
present when modelling a complex system (Crutchfield, 1994b). However, usually
little attention is accorded to the subjective aspects when defining key
concepts for studying such systems. For example, it is not common to find
reference to the involved subjective factors in definitions such as ‘complexity
of complex systems’ or ‘emergence in complex systems’. One of the few examples
in this line is Edmonds’s definition of complexity (Edmonds, 1995; 1999a).
Enveloping allows a modeller to prove properties of
the theory in the model and, having the appropriate validation and verification
of the model, also about the theory against which the model has been verified,
and to bring in new insights to the subject’s cognitive model about the
empirical system. This gives the model a special relevance as it might bring in
changes in both the analytical theory and a modeller’s knowledge. Changes in a
modeller’s knowledge can involve changes of particular beliefs about details of
the unfolding of events in the empirical system, insights about more
fundamental theoretical aspects of the theory in the model, and more general
conclusions about the empirical system.
The idea is to discuss how the notion of envelope
might be used in simulations of chaotic systems. It might, for instance, be of
interest to study closely the behaviour of a certain output around an
attractor. A first envelope could be generated after specifying some constraints
over the model’s parameters to delimit that area of the dependent
(controllable) variables where the attractor is supposed to be generated. This
first approximation would probably not be very precise because, e.g., either
the space of parameters is too wide or the aimed envelope has proved to be too
coarse. After this first envelope has been generated, some experience is won,
‘tighter’ envelopes may be attempted, and further investigation of the tendency
can be carried out. This may be put into practice by redefining either the
specification of the attempted envelope (the theorem to be proved in the case
studied in this thesis) or the constraints over the space of parameters.
This interactive enveloping process would allow a modeller
to learn and to collect data from the experimentation in the computer to
attempt theoretically valid conclusions. Ultimatelly it would assist a modeller
in characterising appropriately (the modeller will decide when to stop
experimenting according to his satisfaction with the results) that region of
parameters and outputs where the behaviour of interest happens. The modeller
will have a set of maps: range of parameters à envelope of outputs.
A hierarchy of modelling architectures, such as that
proposed in Chapter 6, gives a modeller a battery of tools with which he can
obtain complementary information. The automatic implementation of this
architectures in a common platform would help a modeller to deal better with
the complexity of a target system (and its model) than if using a single
architecture. The different and complementary views given by the various
architectural levels can assist modellers in improving their understanding and
in being better informed about the simulated system. A characteristic of the
proposed hierarchy is that, the lower the level of programming, the more
difficult it is for a modeller to understand a simulation, but the wider will
be the fragment of the simulation theory the program will be able to
investigate and the more general will be the conclusions the modeller can draw
from the simulation outputs.
In this thesis a MAS is proposed as the higher level of
programming for modelling a target system that can be well described as the
interaction of components. In many cases MAS are supposed to express the
dynamics of a simulation more flexibly than traditional network-based languages
(e.g., SLAM; Pritsker, 1995). MAS allow for the representation of the evolution
(e.g., certain structural changes) of key elements of a simulation. For
example, the evolution of functions (e.g., that function given the dynamics of
a system) can be easily simulated in a declarative MAS by means of evolving
rules. A rule can be seen as the finest ‘evolving function’ (a function-particle)
and a set of evolving rules as an evolving function. In addition, the
possibility of introducing and eliminating agents seems convenient for
modelling systems components of the simulation system commonly enter and leave.
On the other hand, ideas from MAS could be adapted to model
event-driven simulations more flexible than traditional languages (e.g., SLAM).
Both the network where an entity carries out its cycle of life (this sort of
simulation is explained in Zeigler, 1976) and the entity itself, in an
event-driven simulation, might be represented as agents. The net might be
modelled as a composite agent, which defines the overall system of the
simulation, while the components of the net (e.g., lists, gates, resources)
might be represented as sub-agents. Evolving rules might be used for functions
that give the dynamics of the simulation, such as control of the future event
list (FEL) and event’s consequences (e.g., transition rules implementing change
in the state of the system and further scheduling of events).
A hierarchy of architectures would also help a modeller in
elaborating alternative simplifications of a model (valid under different
experimental frames). For example, using the (logical) model constraint-based
architecture proposed in Chapter 6, different tendencies might be proved, after
which each of them could be used for making a different simplification. Each
simplified model would accurately represent a different aspect of the original
simulation model. Linked to each simplification would be a different
experimental frame, a different output of interest for a modeller, and a
different homomorphism function.
Another way of generating alternative simplifications of a simulation
model is by changing the fragment of the simulation theory explored (see Figure 8.1).
Scientists in the social simulation community are
especially interested in investigating what they have called emergent tendencies
in social systems. However, the notions they use appear to be different from
modeller to modeller. This introduces ambiguity, which seems to be due to the
difficulties in understanding social behaviour. In turn these difficulties
appear to be due in part to the complexity of a social system and to a
modeller’s bounded rationality. A more transparent conception of emergence,
along with more appropriate simulation tools, might help a social modeller to
deal with the complexity of these systems and to understand emergent tendencies
better.
|
|
Figure 8.1. The proposed platform for a hierarchy of
simulation architectures that can be used for different purposes, e.g., for
generating alternative simplified models
|
More concretely, among the achievements of this thesis that
might be useful to the social simulation community, there are: the conception
of emergent tendencies as relative to a subject’s notion of satisfiability and
grounded in a trade-off between objective and subjective aspects, and the
proposal of an automatic platform for translation simulation models among
different programming architectures. The proposed relativistic notion of
emergence of tendencies helps modellers to understand and accept the relativity
of their individual conceptions about the emergence of tendencies, tells them
about the sources of this relativity and may facilitate agreement within the
scientific community. In addition, this might help them decrease the incidence
of polemical discussions. Recognising such relativity would facilitate
modellers’ agreement in discussions about social processes, even when they
disagree about whether particular tendencies observed in those processes are
emergent.
On the other hand, the possibility of proving
restricted homomorphic transformations between models facilitates access to a
variety of procedures for validation, alignment, simplification, and
integration of models, using stronger criteria than those currently used. The
idea is to provide modellers with a methodology allowing the application of the
strong notion of morphism given by Zeigler over fragments of the simulation
theory, rather than the weak notion of approximation as used, for example, in
Monte Carlo techniques. This methodology might be useful, for example: in
drawing more general conclusions about how roles, norms, and organisational
design place bounds on social cognition (in research like that of Carley et
al., 1998); or increasing confidence about detecting gaps, inconsistencies,
or errors in organisational theories (in studies like those of Moss et al., 1998b; Axtell, 1996).
Providing MAS programmers and researchers with a
hierarchy of architectures might help them to deal better with their programs.
For instance, a lower level than the MAS itself would be very helpful for a
programmer in debugging and verifying programs. Moreover, providing automatic
translation into and from other architectures may widen the applicability of
MAS approaches, as more researchers will find them supportive.
It would be convenient to build platforms allowing the
automatic translation of MAS models into other architectures. Different
architectures might be enabled according to a modeller’s interest and needs.
It is the intention of people working on SDML to provide
these kinds of facilities for the social simulation community. In principle,
SDML has been designed specifically for social simulation. At present, it is
intended to provide additional facilities to allow a modeller to prove
tendencies in social processes. The experience gained in developing this thesis
is part of a permanent effort towards adding into SDML more appropriate tools
in accord with a social modeller’s needs. The idea of using MAS architectures
for studying emergent tendencies in a simulation appears to be a novel one.
Among other approaches for using architectural transformation in MAS are:
Ø DeLoach
et al. (2000) suggest building a MAS
by going through a hierarchy of architectural transformations. A methodology,
‘Multiagent Systems Engineering (MaSE)’, and a tool to support it, ‘agentTool’,
are proposed. Their idea is to build a ‘more concrete’ sequence of models in a
‘top-down’ hierarchy of architectural levels, starting from the level of goals.
There, the abstract specification of a MAS, the higher level in the hierarchy,
is captured by a set of goals. This methodology is aimed to help with MAS
verification, facilitating its building in accordance with some abstract
specification, but not to assist in the understanding of the dynamics of a MAS.
Ø Shapiro
et al. (2000) suggest using a
language, ‘Cognitive Agents Specification Language (CASL)’, for specifying and
verifying a MAS. They claim that this language provides a formal specification
allowing abstraction over an agent’s preferences and over agents’ interaction
(messaging) mechanism. This formal representation is also meant to support a
modeller when checking aspects of the agent’s design but not to help in the
understanding of the behaviour of a MAS.
Ø Koen
et al. (2000) use contextual
information for adding flexibility into the behaviour of agents’ using
preference models. In particular, they propose building agents able to ‘adapt’
their plans in an uncertain environment with soft deadlines by using a
context-sensitive planning. They claim these agents have more ‘realistic’
preference models than those commonly used in other approaches. Their idea of a
context-sensitive planning is comparable to the notion of context-driven
exploration of simulation trajectories proposed in this thesis as a second
level of architectural transformations.
Ø The
study of Riley et al. (2000) is
related to understanding MAS and observing aspects of their dynamics; in this
sense it is related to the subjects of interest of this thesis. Concretely,
they propose a ‘layered disclosure by which autonomous agents have included in
their architecture the foundations necessary to allow them to display upon
request the specific reasons for their actions’. In fact, this mechanism
permits a modeller to check the state of the internal model of an agent a at
certain simulation time. This sort of mechanism is programmable in SDML by
writing the specific rules for required reports, or stopping the simulation and
querying the agents’ databases. In addition, SDML allows a modeller to return
to previous states in the simulation. The analysis of the dynamics of a
simulation they propose is quite simple and not so useful for understanding
aspects of the simulation theory. They do not address the more fundamental
aspect of analysing tendencies (and in this way the simulated processes), but
rather aspects at certain isolated simulation instants.
In order to help in clarifying the concept of emergent
tendencies in fields such as that of the social simulation community (where
there are discrepancies about this term), ideas from different areas of
knowledge have been introduced and synthesised to produce the definitions used
in this thesis. For this, I have found the following particularly valuable: a
conception of complexity as relative to a subject’s language (Edmonds, 1998), a
conception of complexity as grounded in the complexity of the object itself (complexity
categorised according to certain levels of phenomena given by Heylighen), and,
finally, basic Kantian ideas about how human beings gather knowledge. The first
two viewpoints were reviewed in Chapter 4. The third, the Kantian view of the
learning process in human beings (which seems to be the starting point for more
elaborate models of knowledge and has been useful in different areas of
research), will be briefly discussed below.
Kant recommended to humans (as subjects) the
following plan for gathering knowledge (following the
interpretation of Solomon (1996)):
1.
There are rules via which a subject interprets its
experience as true – necessarily true.
These are rules, facts, and processes taken as
axioms; among them are:
·
Causality
·
Relativity of a human (subject)’s knowledge
·
Induction
He also claimed that a subject’s reasoning is always about
his own mental models, built in part by using perception of phenomena from the
empirical world, rather than about attributes existing in the empirical world,
since empirical world features cannot be perfectly seized by the cognitive
abilities of a human being.
2.
Any other axiom contradicting the previous ones is
false.
This point assures consistency of the chosen set of
valid axioms while allowing alternative sets of valid axioms. It will permit
the elaboration of different cognitive representations of systems of knowledge.
3.
Other knowledge is either contingently true or
contingently false.
These three first points in Kant’s plan sound like to
a process of elaboration of a logical system; e.g., this point allows the
setting of axioms which are then used to check which knowledge is contingently
true or contingently false via inference rules. In fact, it seems that a
further development of Kant’s ideas gave birth to the first logical
formalisations (see Solomon, 1996) and, further on, they may have served as
basic notions for elaborating cognitive models of agents in artificial
intelligence.
Kant’s plan situates knowledge as relative and
contingent to a subject’s worldview, as finally it is the subject who decides
which axioms he takes as valid. Different subjects might disagree about which
axioms to take as valid.
A social environment seems to have mechanisms for
influencing individuals’ beliefs. Agents’ beliefs and actions are in part
shaped by the set of values and norms taken as ‘normal’ in some society at a
certain time. Different theories have attempted to explain such influence by
different mechanisms. Some of them are found in philosophy, for example in
constructivism. These areas could be helpful in given additional ideas for a
further elaboration of a concept of emergent tendencies.
In the following, it will be argued that knowledge of
systems at different levels of complexity (see Chapter 4) can be
categorised according to these three first points in the Kantian plan. To
eliminate bias in the discussion, it will be assumed that the subject is a
scientist specialised in the area of research and engaged in studying the
phenomena alluded to.
First, consider a physicist observing unanimated matter,
e.g., phenomena at level of complexity one. There is a vast mass of models and
data that are commonly agreed upon, since individuals in that community agree
about much of their knowledge. Hence, a lot of their knowledge is placed at
levels one and two of this plan. However, a good deal of controversy exists in
areas such as fundamental particle physics (these fields would be located at
level three of the Kantian plan).
Now consider knowledge at the following higher level (e.g.,
at the level of living organisms). In this case, the subject is a
biologist. Phenomena can still be discerned using these three first steps
of Kant’s plan. But there seems to exist less agreement about many observed
aspects in the target system than in the case of a physicist observing an
unanimated system (systems at this level undergo new phenomena in addition to
that in the lower level). There will be more controversial issues of knowledge,
i.e., more topics of knowledge at level three. As a result, it seems
biologists’ target systems are at a higher level of complexity than those of
physicists. Emergent tendencies are more likely to appear in a biologist’s
model of his target systems than in physicists’ models of their target systems.
Assume now that the object is social phenomena and
that the subject is a sociologist. It would be even less easy for a
social scientist than for a biologist to find consistent and more general
explanations about tendencies in his target systems, as these are at a higher
level of complexity, since a social scientist places a higher proportion of his
knowledge at a higher level of complexity than does a biologist or a physicist.
A higher proportion of his knowledge will be controversial than in the case of
physicists’.
Finally, it seems that there are phenomena that are
unreachable by human beings’ understanding, for example, phenomena linked to
theological and philosophical questions. Part of such knowledge would be the
content of answers to questions about the existence of a god, or, the less soft
answers to the question whether there exists an ‘absolutely’ correct set of
valid axioms to be taken at level one of the Kantian plan. Questions like the
former of theses (that about the existence of a god) are not considered as
answerable through human beings’ reasoning, as topics in this area are not
practically discernable via experience. This sort of knowledge is considered in
conformity to the next Kantian policy. On the other hand, questions like the
second one seem to tempt humans studying related subjects into endless
discussions.
4.
Phenomena not decidable via experience are not topics
of knowledge.
Exploring the meaning of debatable terms (in this
case related to studying systems at a high level of complexity) by using notions
from thinkers working in foundational areas of knowledge (e.g., philosophy) can
be useful for clarifying such terms. Hopefully, this sort of activity can be
helpful in decreasing controversy within a research community and in
facilitating communication among different research communities.
The aspect of the results achieved in this thesis
that is more relevant for policy analysis is the ‘educative’ orientation of the
proposed platform to assisting the user by allowing translation among different
modelling architectures. In particular, the proposed constraint-based
architecture enables a modeller to establish more general conclusions (as a
wider fragment of the simulation is explored) than does a traditional MAS
exploration. On the other hand, a MAS helps a modeller to improve his
understanding about more specific aspects of a simulation. It is helpful for
obtaining detailed information about the dynamics of single simulation
trajectories.
In an organisation (e.g., a corporation) such a platform can
be used for filtering and providing information relevant to users according to
their role in the organisation in order to improve the behaviour of the whole
corporation, as a complement to the sort of support given by, e.g., traditional
information systems, scenario analysis, and Monte Carlo techniques.
The technique analyses the envelope of tendencies rather
than central measures as in Monte Carlo techniques. Unlike central measures
analysed via Monte Carlo techniques, this confers prominence to tendencies
found in the worst investigated cases. An envelope expresses the outside bounds
of a tendency, so that it may give managers or policy analysts greater
confidence for acting in the system they are modelling compared to an analysis
of central tendencies as in Monte Carlo techniques, which provides only
probabilistic conclusions.
Usually languages used by modellers working in soft
systems such as simulation of social systems have been different from those
used by people working on problems related to harder systems such as
applications in logic-programming and theorem-proving. Nevertheless, in the
last years some groups working in logic-programming have moved towards using
more flexible programming tools. They seek to go from the more traditional
syntactic and backward-chaining mechanisms (e.g., Prolog and OTTER) towards
more flexible tools exploiting better the semantics in a computational model.
An example is that of people working in constraint forward-chaining-based
programming (Frühwirth, et al.,
1992).
A move by the social simulation community towards more
formal tools such as declarative programming also seems convenient. One of the
main advantages of declarative programming is its potential for implementing
formal proofs about the behaviour of a simulation that is difficult in
traditional imperative programming (see Figure
8.2 and the final discussion in Chapters 7 and 8). This
has been the intention of people working at the Centre for Policy Modelling,
Manchester Metropolitan University, when adding the simulation language SDML
facilities for theorem-proving (see Chapter 6). In fact, the experience given
by this thesis is aimed at helping in furthering changes in such a direction.
Thus, me see some convergence between the
theorem-proving and social simulation communities, a convergence that could
hopefully be beneficial to both. This thesis can be seen as a step in this
convergence.
|
|
Figure 8.2. Declarative programming and social simulation
communities’ tools, and recent moves towards common platforms
|
In this thesis, a hierarchy of architectural
transformations for exploring the dynamics of a simulation, a methodology for
proving emergent tendencies in fragments of a simulation theory, a conception
of emergent tendencies aimed at helping in practical modelling applications,
and an envelope of tendencies as an alternative to statistical summaries for
characterising simulation outputs are proposed. They are useful in the
modelling process in terms of their potential to help a modeller in better
understanding the dynamics of a simulation.
For example, in social
simulation, modelling can help to better understand observed tendencies or to
discover new tendencies in a social system. In this case, a hierarchy of
programming architectures (such as that proposed) may provide a modeller with
complementary information about behaviour in a simulation, especially about
emergent tendencies, supporting modelling in both of these tasks. In addition,
a definition of the concept of emergence of tendencies helps strengthen the
support of this hierarchy of architectures for the social simulation community,
as this notion is very important for understanding the processes a social
system undergoes, by helping in clarifying this concept.
It has been argued that the emergence of tendencies is
grounded in a trade-off between objective and subjective aspects. Objective
aspects are linked to an object’s potential for objective complexity, which in
turn depends on the level of complexity of the observed system (as described in
Chapter 4). Conversely, the subjective aspects are related to the difficulties
a subject faces when understanding the system, which are finally linked to a
subject’s language. Moreover, it is recognised that the characterisation of a
tendency as emergent in the end depends on a subject’s judgement. The subject’s
decision depends on his satisfiability with an explanation a model offers about
how the tendency arises. It was argued that the higher the potential for
objective complexity in an object (that system where the tendency has been
perceived by the subject) and the less appropriate for modelling the observed
system the subject’s language is, the higher is the likelihood that the subject
characterises a tendency observed in such an object as emergent.
The hierarchy of architectures of programming that has been
presented is aimed at helping a modeller increase his knowledge about the
target system. The idea is to provide a modeller (conceived as a subject) with
complementary information sources. The higher the level of programming, the
more detail about the simulation the architecture will give, but the smaller
will be the fragment of the simulation theory such architecture can explore. In
this particular study the hierarchy of architectures consists of: a MAS
proposed as the highest level, a (logical) model constraint-based exploration
of trajectories at an intermediate level, and a further system with a syntactic
constraint-based inference mechanism as the lowest level of programming.
Architectures at high levels would be better for exploratory analysis in a
search for tendencies in the simulation, while architectures at low levels
would be more valuable for making restricted proofs of tendencies in the
simulation. In this sense, the last two architectures in the proposed hierarchy
are intended to prove tendencies in a fragment of the simulation theory defined
by a range of parameters of the simulation model and choices of the agents, and
the logic of the simulation language.
A technique and an application were given in Chapter 7 for
the intermediate architectural level. This enabled the investigation of all
simulation trajectories for a range of parameters of the model and choices of
the agents, and a finite number of time levels. This architecture allowed a
restricted proof of tendencies in the case it was applied to.
Similar notions to the proposed hierarchy of architectures
of programming aimed at informing and ‘educating’ a user can be found in
computer science applications, e.g., in databases and information systems. For
example, in some corporations different (information system) architectures are
defined by the different accessibility criteria applied to users at different
levels in the organisational hierarchy for accessing corporative databases.
Thus a user at a low level of the corporative hierarchy of employees would
access very limited data, probably only his personal record, while a manager in
a high position would be much less restricted in accessing the database and
would be able to obtain filtered (useful) information relative to the character
of the decisions he has to take.
The envelope of tendencies in a simulation is an alternative
to traditional statistical measures. It is valuable when exhaustive
investigation of the dynamics of a simulation is pretended, as in
theorem-proving. Moreover, it will hopefully be an option for studying complex
systems overcoming drawbacks of traditional methods such as that pointed out by
Crutchfield: ‘fluctuations dominate behaviour and averages need not be centred
in around the most likely value of its behaviour. This occurs for high
complexity processes…since they have the requisite internal computational
capacity to cause the convergence of observable statistics to deviate from the
Law of Large Numbers’ (Crutchfield, 1992, p. 35).
Among the issues discussed in Chapter 8, is
the trade-off between the computational complexity and the usefulness of these
techniques in some areas of application.
We have thus
satisfied the goals of this thesis, namely:
Ø
To develop a methodological approach for exploring
and proving emergent tendencies in computational models.
Ø
To develop some techniques for implementing such a
methodology.
Ø
To investigate the trade-off between the
computational complexity and the usefulness of these techniques.
Ø
To develop some case studies.
Ø To
review the conception of the emergence of tendencies.
Further work aimed at providing
architectural transformations for better understanding complex systems
includes:
Ø
Implementing the third architecture of programming
proposed in Chapter 7, namely a syntactic constraint-based architecture for
exploring and proving tendencies of behaviour in a simulation.
Ø
Building platforms allowing a modeller to implement
automatic transformations of a single simulation model among different
architectures.
Ø
Making up a more elaborate theory of emergent
tendencies guided by those ideas presented in Chapter 4 and in section 8.6.
Ø
Investigating appropriate architectures of programming
for different modelling applications.
Rules are listed as given by the ‘otter’ option ‘pretty_print’.
In otter, comments are indicated by written before the symbol ‘%’.
This convention will be kept below.
Important points are:
- Rules in otter became clause in ‘usable_list’ (see Chapter 2)
- Initial data (initial state of the system) is place in the list
SOS
- Hyper resolution is used (this is indicated in the first set
used below)
set(hyper_res).
set(prolog_style_variables).
set(really_delete_clauses).
set(pretty_print).
set(split_when_given).
clear(print_new_demod).
clear(print_kept).
clear(print_back_demod).
clear(print_back_sub).
clear(no_fanl).
clear(no_fapl).
clear(print_given).
assign(demod_limit,400000).
make_evaluable(_-_,$DIFF(_,_)).
make_evaluable(_+_,$SUM(_,_)).
make_evaluable(_==_,$EQ(_,_)).
make_evaluable(_/_,$DIV(_,_)).
make_evaluable(_*_,$PROD(_,_)).
make_evaluable(_<=_,$LE(_,_)).
make_evaluable(_>=_,$GE(_,_)).
make_evaluable(_<_,$LT(_,_)).
make_evaluable(_>_,$GT(_,_)).
list(usable).
% Here will be placed clauses corresponding to what in SDML’s
model %initially were rules. Also, the
theorem to be proved will be in this %list
1 [] -Factory(IFactory) | -Delay(Idelay) |
delayFactory(IFactory,Idelay).
%gives the delay for a factory's production (it can also be seen
as delay %in a %trader's purchase
2 [] -Day(‘0’) | initialPrice(‘0.4’).
% gives initial price for one of the producers. The other
producers' %price will
% be a proportion of this value (0.4)
% the next three clauses give producer's price for day 1 (it is an
%initial price):
3 [] -Producer(IProd) | -$ID(IProd,’Producer-1’)
|-initialPrice(Iprice) |
price(IProd,Iprice,’1’,[]).
4 []
-Producer(IProd) |-$ID(IProd,’Producer-2’) |-initialPrice(Iprice)
|
price(IProd,fprod(Iprice,’1.2’),’1’,[]).
5 []
-Producer(IProd) | -$ID(IProd,’Producer-3’) |
-initialPrice(Iprice) |
price(IProd,fprod(Iprice,’1.7’),’1’,[]).
% Once price is given for ‘Producer-1’ at a day (‘It’), and in a
%simulation path whose assumptions are taken in the variable ‘Ia’,
next
%rule generates
% producer's choices for the following day (given as the sum
% of the value in ‘It’ and 1. The last parameter in the clause
% ‘listSelProDay’ gives the assumption for that choice. This
assumption
% will be concatenated with the previous assumptions in ‘Ia’ for
% identifying data in the new branches.
6 [] -price(‘Producer-1’,Iprice,It,Ia) |
listSelProDay(‘Producer-2’,’Producer-1’,’Producer-1’,$FSUM(It,’1’),1)
|
listSelProDay(‘Producer-2’,’Producer-1’,’Producer-2’,$FSUM(It,’1’),2)
|
listSelProDay(‘Producer-2’,’Producer-3’,’Producer-1’,$FSUM(It,’1’),3)
|
listSelProDay(‘Producer-2’,’Producer-3’,’Producer-2’,$FSUM(It,’1’),4)
|
listSelProDay(‘Producer-3’,’Producer-1’,’Producer-1’,$FSUM(It,’1’),5)
|
listSelProDay(‘Producer-3’,’Producer-1’,’Producer-2’,$FSUM(It,’1’),6)
|
listSelProDay(‘Producer-3’,’Producer-3’,’Producer-1’,$FSUM(It,’1’),7)
|
listSelProDay(‘Producer-3’,’Producer-3’,’Producer-2’,$FSUM(It,’1’),8).
% Next clause calculates price. Notice that data used in the
precedent
% (having the symbol ‘-’
preceding the clause) is checked to be sure
% they have the same assumption, expect listSelProDay which bring
the new
% assumption (‘Newa’). In the consequent the new price has as the
% assumption the concatenation of the old assumptions
%(‘Ia’) and the new one ‘Newa’. This price corresponds to a new
iteration
%than that of the data used in the precedent. The new assumption
for the %new branch is brought in the variable ‘Nt’ of the clause
%’listSelProDay’. The final manipulations to calculate price are left to % a
demodulator ‘demprice’.
% Demodulators work in a similar way than backward-chaining rules
in
% SDML: their intermediate results are not written in the database
-only
% the final result is returned.
7 []
-Producer(Iprod) |
-price(Iprod,Ioldprice,It,Ia) |
-maxDays(ImaxDays) |
-saleProd(Iprod,Mysales,It,Ia) |
-$FLE(It,ImaxDays) |
-saletot(Totsales,It,Ia) |
-price(‘Producer-1’,Ioldprice1,It,Ia) |
-price(‘Producer-2’,Ioldprice2,It,Ia) |
-price(‘Producer-3’,Ioldprice3,It,Ia) |
-listSelProDay(Isel1,Isel2,Isel3,Nt,Newa) |
-$FEQ(Nt,$FSUM(It,’1’)) |
-price(Isel1,Icomprice1,It,Ia) |
-price(Isel2,Icomprice2,It,Ia) |
-price(Isel3,Icomprice3,It,Ia) |
-pp1(Ip1,Ip2) |
price(
Iprod,
demprice(
Iprod,
Ioldprice,
Ioldprice1,
Ioldprice2,
Ioldprice3,
Icomprice1,
Icomprice2,
Icomprice3,
Mysales,
Totsales,
Ip1,
Ip2,
‘0.5’
),
Nt,
[Newa|Ia]
).
% This rule is responsible for given the initial production of a
factory,
% e.g., % production at day 1. Notice that the list of assumptions
(last
% field in the predicate ‘productionDay’) is empty.
8 []
-Producer(IProd) |
-storeOwner(IStore,IProd) |
-factoryOwner(IFact,IProd) |
-maxCapacity(IFact,Max) |
productionDay(IFact,Max,’1’,[]).
%Next rule is responsible for setting production of a Producers’
% factories or setting traders’ purchases). It can be seen that
the value
% at present (iteration ‘Nt’) depends of the value of such a
production
% at the previous iteration ‘Ia’.
This rule is a translation into a
% clause in OTTER of the corresponding rule in SDML. A demodulator
is
% used -to calculate production
9 []
-Producer(IProd) |
-storeOwner(IStore,IProd) |
-factoryOwner(IFact,IProd) |
-maxCapacity(IFact,Max) |
-level(IStore,Ilevelstore,IDay,Ia) |
-$FGE(IDay,’1’) |
-orderprod(IProd,ITot,Nt,[Newa|Ia]) |
-$FEQ($FSUM(IDay,’1’),Nt) |
-delayFactory(IFact,Idelay) |
-capacityStore(IStore,Icapacity) |
productionDay(
IFact,
DemProd(Max,Icapacity,Ilevelstore,ITot,Idelay),
Nt,
[Newa|Ia]
).
% Clauses 10 and 11 are responsible for setting store’s level.
Clause 10
% sets initial level at time 1, while clause 11 updates level as
time
% goes on. Some built in demodulators OTTER offers are used to
calculated
% a sum and a difference.
10 []
-Producer(IProd) |
-storeOwner(IStore,IProd) |
-factoryOwner(IFact,IProd) |
-productionDay(IFact,Iproductionday,’1’,Ia) |
level(IStore,Iproductionday,’1’,Ia).
11 []
-storeOwner(IStore,IProd) |
-factoryOwner(IFact,IProd) |
-productionDay(IFact,Iproductionday,Nt,[Newa|Ia]) |
-maxDays(IMaxDays) |
-level(IStore,Iyesterdaylevel,It,Ia) |
-$FGE(IMaxDays,Nt) |
-$FEQ(Nt,$FSUM(It,’1’)) |
-saleProd(IProd,Isaleprod,It,Ia) |
level(
IStore,
$FDIFF($FSUM(Iyesterdaylevel,Iproductionday),Isaleprod),
Nt,
[Newa|Ia]
).
%Clause 12 is responsible for setting producers’ (traders’) sales
at
% iteration Ia.
12 []
-order(Icons,Iprod,Itotcons,Nt,Ia) |
-level(Istore,Ilevel,Nt,Ia) |
-storeOwner(Istore,Iprod) |
-orderprod(Iprod,Itotal,Nt,Ia) |
sale(
Iprod,
Icons,
$IF(
$FGE(Ilevel,Itotal),
Itotcons,
$IF(
$FEQ(Itotal,’0’),
‘0’,
TruncPos($FPROD(Ilevel,$FDIV(Itotcons,Itotal)))
)
),
Nt,
Ia
).
% Clauses 13 and 14 give consumers (distributors)’ demand. Clause
13
% gives the initial demand at iteration 1, and clause 14 is
responsible
% for updating this value at each state transition
13 []
-Consumer(Iconsumer) |
-Producer(Iproducer) |
-maxDays(InoD) |
-demandRange(Imin,Imax) |
-selProd(Iprodsel,Nt,Ia) |
-$FEQ(Nt,’1’) |
demand(Iconsumer,demnD(Nt,InoD,Imin,Imax),’1’,[]).
14 []
-Consumer(Iconsumer) |
-Producer(Iproducer) |
-maxDays(InoD) |
-demandRange(Imin,Imax) |
-demand(Iconsumer,Ioldlevel,It,Ia) |
-order(Iconsumer,Iproducer,Ioldorder,It,Ia) |
-salecons(Iconsumer,Isalecons,It,Ia) |
-sale(Iproducer,Iconsumer,Isale,It,Ia) |
-selProd(Iprodsel,Nt,[Newa|Ia]) |
-$FGT(Nt,’1’) |
-$FEQ(It,$FDIFF(Nt,’1’)) |
demand(
Iconsumer,
$FDIFF($FSUM(demnD(Nt,InoD,Imin,Imax),Ioldlevel),Isalecons),
Nt,
[Newa|Ia]
).
% Clause 15 gives the initial consumer (distributor) order and
clause 16
% updates order for each state transition
15 []
-Consumer(Iconsumer) |
-Producer(Iproducer) |
-maxDays(InoD) |
-demandRange(Imin,Imax) |
-selProd(Iprodsel,Nt,Ia) |
-$FEQ(Nt,’1’) |
order(
Iconsumer,
Iproducer,
$IF($ID(Iprodsel,Iproducer),demnD(Nt,InoD,Imin,Imax),’0’),
‘1’,
Ia
).
16 []
-Consumer(Iconsumer) |
-Producer(Iproducer) |
-maxDays(InoD) |
-demandRange(Imin,Imax) |
-demand(Iconsumer,Ioldlevel,It,Ia) |
-order(Iconsumer,Iproducer,Ioldorder,It,Ia) |
-salecons(Iconsumer,Isalecons,It,Ia) |
-sale(Iproducer,Iconsumer,Isale,It,Ia) |
-selProd(Iprodsel,Nt,[Newa|Ia]) |
-$FGT(Nt,’1’) |
-$FEQ(It,$FDIFF(Nt,’1’)) |
order(
Iconsumer,
Iproducer,
$FDIFF(
$FSUM(
$IF($ID(Iprodsel,Iproducer),demnD(Nt,InoD,Imin,Imax),’0’),
Ioldorder
),
Isale
),
Nt,
[Newa|Ia]
).
% This clause (17) is used to find that producer with the lowest
price at
% iteration Ia. The prices at that iteration are the input to the
% demodulator ‘demSelProd’ responsible for returning the required
% producer.
17 []
-price(‘Producer-1’,Iprice1,Nt,Ia) |
-price(‘Producer-2’,Iprice2,Nt,Ia) |
-price(‘Producer-3’,Iprice3,Nt,Ia) |
selProd(demSelProd(Iprice1,Iprice2,Iprice3),Nt,Ia).
% Next clauses, from 18 to 21, are used for calculating total
orders and
% total sales by producer (trader) and consumer (distributor).
18 []
-order(‘Consumer-1’,Iproducer,Iorder1,It,Ia) |
-order(‘Consumer-2’,Iproducer,Iorder2,It,Ia) |
-order(‘Consumer-3’,Iproducer,Iorder3,It,Ia) |
orderprod(Iproducer,$FSUM($FSUM(Iorder1,Iorder2),Iorder3),It,Ia).
19 []
-sale(Iproducer,’Consumer-1’,Isale1,It,Ia) |
-sale(Iproducer,’Consumer-2’,Isale2,It,Ia) |
-sale(Iproducer,’Consumer-3’,Isale3,It,Ia) |
saleProd(Iproducer,$FSUM($FSUM(Isale1,Isale2),Isale3),It,Ia).
20 []
-sale(‘Producer-1’,Iconsumer,Isale1,It,Ia) |
-sale(‘Producer-2’,Iconsumer,Isale2,It,Ia) |
-sale(‘Producer-3’,Iconsumer,Isale3,It,Ia) |
salecons(Iconsumer,$FSUM($FSUM(Isale1,Isale2),Isale3),It,Ia).
21 []
-salecons(‘Consumer-1’,Isale1,It,Ia) |
-salecons(‘Consumer-2’,Isale2,It,Ia) |
-salecons(‘Consumer-3’,Isale3,It,Ia) |
saletot($FSUM($FSUM(Isale1,Isale2),Isale3),It,Ia).
% Next rule is the theorem. First, the data is brought in:
Producer’s
% prices at time Time1, time2 and time3, whose values are
iterationg 1, 4
% and 7 as seen in the 10th clause. Afterwards, it is checked
if the size
% of the intervals for prices is decreasing. There, two OTTER’s
built in
% facilities are used: $FGE, which means grater or equal than, and
‘$AND’
% used to evaluate disjunctions.
% The size of the interval of prices is calculated by the
demodulator
% ‘Interval’. In case the theorem is true the clause
‘–Contradition(1)’
% is generated creating a contradiction as the clause
‘Contradiction(1)
% has been already put in the database (this clause is produced in
the
% list ‘sos’, see below). This theorem not necessarily is the one
% reported in the thesis – this one checks only for not increase
in the
% interval of prices for days 1, 4 and 7.
22 []
-price(‘Producer-1’,Iprice11,Time1,Ia1) |
-price(‘Producer-2’,Iprice12,Time1,Ia1) |
-price(‘Producer-3’,Iprice13,Time1,Ia1) |
-price(‘Producer-1’,Iprice21,Time2,Ia2) |
-price(‘Producer-2’,Iprice22,Time2,Ia2) |
-price(‘Producer-3’,Iprice23,Time2,Ia2) |
-price(‘Producer-1’,Iprice31,Time3,Ia3) |
-price(‘Producer-2’,Iprice32,Time3,Ia3) |
-price(‘Producer-3’,Iprice33,Time3,Ia3) |
-$AND($AND($FEQ(Time1,’1’),$FEQ(Time2,’4’)),$FEQ(Time3,’7’)) |
-$FGE(Interval(Iprice11,Iprice12,Iprice13),Interval(Iprice21,Iprice22,Iprice23))
|
-$FGE(Interval(Iprice21,Iprice22,Iprice23),Interval(Iprice31,Iprice32,Iprice33))
|
-Contradiction(1).
end_of_list.
% Next list define OTTER demodulators used above for calculations.
They
% work as backward-chaining rules in SDML list(demodulators).
% This demodulator calculates traders (producers)’ prices
23 []
=(
demprice(
Iprod,
Ioldprice,
Ioldprice1,
Ioldprice2,
Ioldprice3,
Icomprice1,
Icomprice2,
Icomprice3,
Mysales,
Totsales,
Ip1,
Ip2,
‘0.5’
),
$IF(
$FGT(comp(Mysales,Totsales),’0’),
$FSUM(
Ioldprice,
$FPROD(
‘0.5’,
$FPROD(
Ip1,
add(
Iprod,
Ioldprice1,
Ioldprice2,
Ioldprice3,
Icomprice1,
Icomprice2,
Icomprice3
)
)
)
),
$IF(
$AND(
$FLT(comp(Mysales,Totsales),’0’),
$FGE(
$FDIFF(
Ioldprice,
$FPROD(
‘0.5’,
$FPROD(
Ip1,
add(
Iprod,
Ioldprice1,
Ioldprice2,
Ioldprice3,
Icomprice1,
Icomprice2,
Icomprice3
)
)
)
),
‘0.05’
)
),
$FDIFF(
Ioldprice,
$FPROD(
‘0.5’,
$FPROD(
Ip1,
add(
Iprod,
Ioldprice1,
Ioldprice2,
Ioldprice3,
Icomprice1,
Icomprice2,
Icomprice3
)
)
)
),
Ioldprice
)
)
).
% Next demodulator calculates the difference between a producer’s
sales
% and the mean of producer’s sales. It is used by the demodulator
% ‘demprice’.
24 []
comp(Mysales,Totsales)=$FDIFF(Mysales,$FDIV(Totsales,’3’)).
%This demodulator gives the biggest difference between any pair of
three
%numbers. It is used for calculating the size of the interval of
prices
% at %certain day.
25 []
=(
Interval(Iprice11,Iprice12,Iprice13),
$FDIFF(fmax3(Iprice11,Iprice12,Iprice13),fmin3(Iprice11,Iprice12,Iprice13))
).
% Next demodulator is used for calculating producers’ demand
26 []
=(
DemProd(Max,Icapacity,Ilevelstore,Itot,Idelay),
fmax2(
TruncPos($FDIV(Max,’4’)),
fmin2(
Max,
fmin2($FDIFF(Icapacity,Ilevelstore),TruncPos($FDIV(Itot,Idelay)))
)
)
).
% Next demodulator is used for determining the producer with the
lowest
% price.
% It uses as auxiliary demodulators ‘demSelProdi’, i = 1,2, …7;
e.g.,
% demodultores from 28 to 34.
27 []
=(
demSelProd(Iprice1,Iprice2,Iprice3),
$IF(
$AND($FLT(Iprice1,Iprice2),$FLT(Iprice1,Iprice3)),
‘Producer-1’,
demSelProd1(Iprice1,Iprice2,Iprice3)
)
).
28 []
=(
demSelProd1(Iprice1,Iprice2,Iprice3),
$IF(
$AND($FEQ(Iprice1,Iprice2),$FLT(Iprice1,Iprice3)),
‘Producer-1’,
demSelProd2(Iprice1,Iprice2,Iprice3)
)
).
29 []
=(
demSelProd2(Iprice1,Iprice2,Iprice3),
$IF(
$AND($FLT(Iprice1,Iprice2),$FEQ(Iprice1,Iprice3)),
‘Producer-1’,
demSelProd3(Iprice1,Iprice2,Iprice3)
)
).
30 []
=(
demSelProd3(Iprice1,Iprice2,Iprice3),
$IF(
$AND($FLT(Iprice1,Iprice2),$FEQ(Iprice2,Iprice3)),
‘Producer-1’,
demSelProd4(Iprice1,Iprice2,Iprice3)
)
).
31 []
=(
demSelProd4(Iprice1,Iprice2,Iprice3),
$IF(
$AND($FLT(Iprice2,Iprice1),$FLT(Iprice2,Iprice3)),
‘Producer-2’,
demSelProd5(Iprice1,Iprice2,Iprice3)
)
).
32 []
=(
demSelProd5(Iprice1,Iprice2,Iprice3),
$IF(
$AND($FLT(Iprice2,Iprice1),$FEQ(Iprice1,Iprice3)),
‘Producer-2’,
demSelProd6(Iprice1,Iprice2,Iprice3)
)
).
33 []
=(
demSelProd6(Iprice1,Iprice2,Iprice3),
$IF(
$AND($FLT(Iprice2,Iprice1),$FEQ(Iprice2,Iprice3)),
‘Producer-2’,
demSelProd7(Iprice1,Iprice2,Iprice3)
)
).
34 []
=(
demSelProd7(Iprice1,Iprice2,Iprice3),
$IF(
$AND($FEQ(Iprice1,Iprice2),$FEQ(Iprice1,Iprice3)),
‘Producer-2’,
‘Producer-3’
)
).
% This demodulator (35) is used to calculate consumers’ new demand
35 []
=(
demnD(Nt,InoD,Imin,Imax),
TruncPos(
$FPROD(
‘0.8’,
$FPROD(
fmedia(Imin,Imax),
$FSUM(‘1’,$FPROD(‘0.5’,$FDIV($FDIFF(Nt,’1’),$FDIFF(InoD,’1’))))
)
)
)
).
% The following demodulator (35) is used to trunk a non-negative
‘real’
% (float point number) ‘A’. First, the demodulator checks if it is
% between 0 and 1, in such a case then the answer is 0, in other
case
% demodulator ‘Trunck1’ (demodulator 36) is called which
recursively will
% check if the number is between B and B+1 starting with B = 1.
This
% demodulator is used when calculating sales.
36 []
TruncPos(A)=$IF($AND($FLE(‘0’,A),$FGT(‘1’,A)),’0’,Trunc1(A,’1’)).
37 []
Trunc1(A,B)=$IF($AND($FLE(B,A),$FGT($FSUM(B,’1’),A)),B,Trunc1(A,$FSUM(B,’1’))).
% The following demodulator returns the absolute value of the
difference
% between a producer’s price (Ioldpricei in case of producer-i, i
=
% 1,2,3) and the price of the selected (chosen) producer for
comparing
% prices (value kept in the variable Icompricei, i = 1,2,3). This
% demodulator is called from the demodulator used for
price-setting
% (‘demprice’).
38 []
=(
add(
Iprod,
Ioldprice1,
Ioldprice2,
Ioldprice3,
Icomprice1,
Icomprice2,
Icomprice3
),
$IF(
$ID(Iprod,’Producer-1’),
fabsdif(Ioldprice1,Icomprice1),
$IF(
$ID(Iprod,’Producer-2’),
fabsdif(Ioldprice2,Icomprice2),
fabsdif(Ioldprice3,Icomprice3)
)
)
).
% Next demodulator is used in add to calculate the absolute value
of the
% difference between A and B
39 []
fabsdif(A,B)=$IF($FGE($FDIFF(A,B),’0’),$FDIFF(A,B),$FDIFF(B,A)).
% clause 40 calculates mean value between two integers Min and Max
and
% clause 41 calculates the mean of two float point numbers.
40 [] media(Min,Max)=sum(Min,Max)/2.
41 [] fmedia(Min,Max)=$FDIV($FSUM(Min,Max),’2’).
42 [] dif(A,B)=A-B. % calculates the difference between A and B
(integers)
43 [] div(A,B)=A/B. % calculates the division between A and B
(integers)
44 [] sum(A,B)=$SUM(A,B). % calculate the sum between A and B
(integers)
% Next demodulators are responsible for trivial operations
deducible from
% the demodulator itself and so no additional comment will be
placed.
45 [] proddiv(A,B,C)=prod(A,B)/C.
46 [] demod1(A,B)=dif(A,B)*3.
47 [] demod2(A,B)=demod1(A,B)/2.
48 [] prod(A,B)=A*B.
49 [] fprod(A,B)=$FPROD(A,B).
50 [] min2(A,B)=$IF(A<=B,A,B).
51 [] max2(A,B)=$IF(A>=B,A,B).
52 [] fmin2(A,B)=$IF($FLE(A,B),A,B).
53 [] fmin3(A,B,C)=$IF($AND($FLE(A,B),$FLE(A,C)),A,fmin2(B,C)).
54 [] fmax2(A,B)=$IF($FGE(A,B),A,B).
55 [] fmax3(A,B,C)=$IF($AND($FGE(A,B),$FGE(A,C)),A,fmax2(B,C)).
56 [] total([])=0.
57 [] total([X|Z])=total(Z)+X.
end_of_list.
list(sos).
% This list places in the rulebase initial data and parameters.
% Next predicate is used to check the theorem. If the theorem is
true the
% predicate ‘-Contradiction(1)’ is generated creating a
contradiction in
% the search path. If that happens OTTER backtracks to search into
% another branch
Contradiction(1).
Day(‘0’). %auxiliary clause used when generating the initial price
% Below other predicates like those indicating capacity of store,
maximum
% capacity of a factory, names of factories, stores, producer
owner of
% factories and stores and producers and consumers’ names are
given
capacityStore(‘Store-1’,’750’).
capacityStore(‘Store-2’,’750’).
capacityStore(‘Store-3’,’750’).
listProd(‘Producer-1’,’Producer-2’,’Producer-3’).
maxCapacity(‘Factory-1’,’750’).
maxCapacity(‘Factory-2’,’750’).
maxCapacity(‘Factory-3’,’750’).
maxDays(‘8’).
Factory(‘Factory-1’).
Factory(‘Factory-2’).
Factory(‘Factory-3’).
Delay(‘4’).
Store(‘Store-1’).
Store(‘Store-2’).
Store(‘Store-3’).
factoryOwner(‘Factory-1’,’Producer-1’).
storeOwner(‘Store-1’,’Producer-1’).
factoryOwner(‘Factory-2’,’Producer-2’).
storeOwner(‘Store-2’,’Producer-2’).
factoryOwner(‘Factory-3’,’Producer-3’).
storeOwner(‘Store-3’,’Producer-3’).
Consumer(‘Consumer-1’).
Producer(‘Producer-1’).
Consumer(‘Consumer-2’).
Producer(‘Producer-2’).
Consumer(‘Consumer-3’).
Producer(‘Producer-3’).
% Other initialisations are given below (e.g., number of factories
in the
% simulation and the predicates ‘orderprod’ and ‘salecons’ at time
‘0’,
% which do not have significance in the model, but are used as fictitious
% data to make some rules more general):pp1(‘1’,’1’).
demandRange(‘200’,’300’).
noOfConsumers(1).
noOfProducers(1).
noOfFactories(1).
noOfStores(1).
salecons(‘Consumer-1’,’0’,’0’,[]).
salecons(‘Consumer-2’,’0’,’0’,[]).
salecons(‘Consumer-3’,’0’,’0’,[]).
orderprod(‘Producer-3’,’0’,’0’,[]).
orderprod(‘Producer-1’,’0’,’0’,[]).
orderprod(‘Producer-2’,’0’,’0’,[]).
saleProd(‘Producer-1’,’0’,’0’,[]).
saleProd(‘Producer-2’,’0’,’0’,[]).
saleProd(‘Producer-3’,’0’,’0’,[]).
saletot(‘0’,’0’,[]).
order(‘Consumer-1’,’Producer-1’,’0’,’0’,[]).
order(‘Consumer-2’,’Producer-1’,’0’,’0’,[]).
order(‘Consumer-3’,’Producer-1’,’0’,’0’,[]).
order(‘Consumer-1’,’Producer-2’,’0’,’0’,[]).
order(‘Consumer-2’,’Producer-2’,’0’,’0’,[]).
order(‘Consumer-3’,’Producer-2’,’0’,’0’,[]).
order(‘Consumer-1’,’Producer-3’,’0’,’0’,[]).
order(‘Consumer-2’,’Producer-3’,’0’,’0’,[]).
order(‘Consumer-3’,’Producer-3’,’0’,’0’,[]).
sale(‘Producer-1’,’Consumer-1’,’0’,’0’,[]).
sale(‘Producer-2’,’Consumer-1’,’0’,’0’,[]).
sale(‘Producer-3’,’Consumer-1’,’0’,’0’,[]).
sale(‘Producer-1’,’Consumer-2’,’0’,’0’,[]).
sale(‘Producer-2’,’Consumer-2’,’0’,’0’,[]).
sale(‘Producer-3’,’Consumer-2’,’0’,’0’,[]).
sale(‘Producer-1’,’Consumer-3’,’0’,’0’,[]).
sale(‘Producer-2’,’Consumer-3’,’0’,’0’,[]).
sale(‘Producer-3’,’Consumer-3’,’0’,’0’,[]).
end_of_list.
The forward-chaining rules driven the search are listed first.
Then, at the end, of this list, the list of backward-chaining rules will be
given.
Rulebase: proving (n)>ModelAgent (content)
----------------------------------------------------------------------
Rule: alternatives for delay delivering (parameters)
Antecedents:
or
is ?p2 4\
is ?p2 10
Consequents:
p2 ?p2
Comment:
Gives delay for producers’ purchasing. In fact only one
alternative (4) will be used
----------------------------------------------------------------------
Rule: create consumers (create)
Antecedents:
and
namedInstance ?cons1
Consumer ‘consumer-1’\
namedInstance ?cons2
Consumer ‘consumer-2’\
namedInstance ?cons3
Consumer ‘consumer-3’\
= ?list [?cons1 ?cons2
?cons3]
Consequents:
and
consumer ?cons1\
consumer ?cons2\
consumer ?cons3\
listCons ?list
Commment:
Create objects consumers (distributors) and a list with pointers
to them at the beginning of the simulation
----------------------------------------------------------------------
Rule: create producers (create)
Antecedents:
and
namedInstance ?prod1
Producer ‘producer-1’\
namedInstance ?prod2
Producer ‘producer-2’\
namedInstance ?prod3
Producer ‘producer-3’\
= ?list [?prod1 ?prod2
?prod3]
Consequents:
and
listProd ?list\
producer ?prod1\
producer ?prod2\
producer ?prod3
Commment:
Create objects producers (traders) and a list with pointers to
them at the beginning of the simulation
----------------------------------------------------------------------
Rule: create stores and factories (create)
Antecedents:
and
producer ?producer\
noOfFactories ?no1\
noOfStores ?no3\
inInterval ?i 1 ?no1\
inInterval ?k 1 ?no3\
generatedInstance
?factory Factory [?i ?producer]\
generatedInstance
?store Store [?k ?producer]
Consequents:
and
factory ?factory\
store ?store\
factoryOwner ?factory
?producer\
storeOwner ?store
?producer
Commment:
Create factory and stores. The additional clauses indexes them to
the owner producer.
----------------------------------------------------------------------
Rule: delay and maxcapacity values ... (parameters)
Antecedents:
and
factory ?factory\
demandRange ?min ?max\
is ?maxcap ?max - ?min\
truncated ?tmaxcap
?maxcap\
is ?prom (?max + ?min)
/ 2\
truncated ?promt ?prom\
is ?maxprod 3 * ?promt\
is ?cap 3 * ?max\
randomChoice ?p2r ?p2 1
p2 ?p2
Consequents:
and
delay ?factory ?p2r\
maxCapacity ?factory
?maxprod
Comment:
This rule gives: first the delay trader's get their purchase. It
is take as a random choice, but the simulation was run only for one.
The second value in the consequent is the maximum (upper bound)
amount a factory of producer can produce (factory production corresponds to a trader’s
purchase).
----------------------------------------------------------------------
Rule: demand range (parameters)
Antecedents:
and
= ?min 200\
= ?max 300
Consequents:
demandRange ?min ?max
Comment:
Rule given what initially was thought as the range of demand … two
values used when calculating demand.
----------------------------------------------------------------------
Rule: end simulation (simulation, start, end)
Antecedents:
and
time day ?dayar\
greater ?dayar 1
Consequents:
and
final day
Comment:
This rules is used to stop the simulation.
The module ‘model’ keeps its internal time at 1 while the proof is
going on. The time of the model (which is changing) is manipulated explicitly
as it can be seen in the clauses.
As soon as the proof is successful and there is not possible
backtracking at time 1 of the module it goes to time 2 and then this rule stops
the simulation.
----------------------------------------------------------------------
Rule: error computer (simulation, start, end)
Antecedents:
and
= ?errorFactor
100000000\
is ?roundError 1 /
?errorFactor
Consequents:
and
errorFactor 100000000\
roundError ?roundError
Comment:
This rule is used to deal with round error in the simulation. Two
values whose difference is too small might be considered equal. The computer
round error might be greater than the difference between the numbers. The idea
is that when comparing two numbers if their difference is smaller than this
error (given above as ?roundError) then the numbers are equal for practical
purposes. This idea is used when checking the theorem for comparing the
monotonic behaviour of the amplitude of the interval of prices. If the
difference between the amplitude of two intervals is smaller than this value,
then the intervals are assumed to be of similar size.
----------------------------------------------------------------------
Rule: factor for minimum price, factor for delta price
(parameters)
Antecedents:
true
Consequents:
and
factorDeltaPrice 0.5\
factorMinimumPrice 0.3
Commment:
Obsolete?…
Gives a parameter factorMinimumPrice to be used to set lower bound
for price, and a parameter (factorDeltaPrice) used when changing prices.
----------------------------------------------------------------------
Rule: initialice demand, order
(initializing)
Antecedents:
and
producer ?prod\
consumer ?cons\
calcDemand ?idem and [1]\
listSelProd1 [?prodsel
?other1 ?other2]\
calcNewOrder ?prod
?prodsel ?idem and ?ordervalue
Consequents:
and
demand1 ?cons ?idem and\
order1 ?cons ?prod
?ordervalue
Comment:
Sets the demand for each consumer, where the new demand for each
day
is calculated according to a linear increasing function. The total
demand of the consumer is the addition of the demand of the day
and the
previous accumulated demand (or demand of the last day) minus the
sales
at present day.
Each consumer places an order to each producer, among which only
one is
different from zero. This is placed at that producers with the
lowest price.
noOfDays is used to determine the slop of the function. It is
assumed that
the demand at the end of the simulation period is twice the
initial demand.
In this case this rule is very specific and only given the initial
values at time 1.
----------------------------------------------------------------------
Rule: initialice OrderCons, OrderProd (initializing)
Antecedents:
and
listCons ?listCons\
= ?listCons [?cons1
?cons2 ?cons3]\
listProd ?listProd\
= ?listProd [?prod1
?prod2 ?prod3]\
order1 ?cons1 ?prod1
?s1\
order1 ?cons2 ?prod1
?s2\
order1 ?cons3 ?prod1
?s3\
order1 ?cons1 ?prod2
?s4\
order1 ?cons2 ?prod2
?s5\
order1 ?cons3 ?prod2
?s6\
order1 ?cons1 ?prod3
?s7\
order1 ?cons2 ?prod3
?s8\
order1 ?cons3 ?prod3
?s9\
is ?order1 ?s1 + ?s4 +
?s7\
is ?order2 ?s2 + ?s5 +
?s8\
is ?order3 ?s3 + ?s6 +
?s9\
is ?orderp1 ?s1 + ?s2 +
?s3\
is ?orderp2 ?s4 + ?s5 +
?s6\
is ?orderp3 ?s7 + ?s8 +
?s9
Consequents:
and
orderCons1 ?cons1
?order1\
orderCons1 ?cons2
?order2\
orderCons1 ?cons3
?order3\
orderProd1 ?prod1
?orderp1\
orderProd1 ?prod2
?orderp2\
orderProd1 ?prod3
?orderp3
Comment:
Gives the total orders by producers and consumers at the initial
simulation time.
----------------------------------------------------------------------
Rule: initialice price (initializing)
Antecedents:
and
iPrice ?iPrice\
factoriPrice1 ?fiP1\
factoriPrice2 ?fiP2\
listProd ?listProd\
= ?listProd [?prod1
?prod2 ?prod3]\
= ?iprice1 ?iPrice\
is ?iprice2 ?iPrice *
?fiP1\
is ?iprice3 ?iPrice *
?fiP2
Consequents:
and
price1 ?prod1 ?iprice1\
price1 ?prod2 ?iprice2\
price1 ?prod3 ?iprice3
Comment:
Rule for initialising prices at time 1. Producer’s 1 prices is as
given in ?iPrice in the beginning of the simulation an the other slightly
different according to the two factors given in ?fiP1, fiP2. In the original
model (before splitting) this factors were introduced directly in the rule.
----------------------------------------------------------------------
Rule: initialice price param. (initializing)
Antecedents:
true
Consequents:
and
iPrice 0.4\
factoriPrice1 1.2\
factoriPrice2 1.7
Comment:
Rule given parameters for prices.
Initial price will be set at 0.4 for a producer, and for the
others, it will be set as these values multiplied by factoriPrice1 and by
factoriPrice2.
----------------------------------------------------------------------
Rule: initialise production day and level (initialising)
Antecedents:
and
store ?store\
factory ?factory\
demandRange ?min ?max\
is ?maxcap ?max - ?min\
truncated ?tmaxcap
?maxcap\
is ?prom (?max + ?min)
/ 2\
truncated ?promt ?prom\
is ?maxprod 3 * ?promt\
is ?cap 3 * ?promt
Consequents:
and
productionDay1 ?factory
?cap\
level1 ?store ?cap\
capacityStore ?store
?cap
Comment:
Rule to initialise production of factory (equal to its capacity)
and level of store at day 1. Also max. capacity of store is set ot ?cap.
----------------------------------------------------------------------
Rule: initialice sales (initializing)
Antecedents:
and
consumer ?consumer\
producer ?producer\
level1 ?store
?levelStore\
storeOwner ?store
?producer\
order1 ?consumer
?producer ?orderConsProd\
level1 ?store
?levelStore\
orderProd1 ?producer
?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale1 ?producer ?consumer ?saleValue
Comment:
Determines a producer’s (initial) sales for a consumer at day 1.
----------------------------------------------------------------------
Rule: initialice SalesCons, SalesProd (initializing)
Antecedents:
and
listCons ?listCons\
= ?listCons [?cons1
?cons2 ?cons3]\
listProd ?listProd\
= ?listProd [?prod1
?prod2 ?prod3]\
sale1 ?prod1 ?cons1
?s1\
sale1 ?prod1 ?cons2
?s2\
sale1 ?prod1 ?cons3
?s3\
sale1 ?prod2 ?cons1
?s4\
sale1 ?prod2 ?cons2
?s5\
sale1 ?prod2 ?cons3
?s6\
sale1 ?prod3 ?cons1
?s7\
sale1 ?prod3 ?cons2
?s8\
sale1 ?prod3 ?cons3
?s9\
is ?salec1 ?s1 + ?s4 +
?s7\
is ?salec2 ?s2 + ?s5 +
?s8\
is ?salec3 ?s3 + ?s6 +
?s9\
is ?salep1 ?s1 + ?s2 +
?s3\
is ?salep2 ?s4 + ?s5 +
?s6\
is ?salep3 ?s7 + ?s8 +
?s9\
is ?totalSales ?salec1
+ ?salec2 + ?salec3
Consequents:
and
saleCons1 ?cons1
?salec1\
saleCons1 ?cons2
?salec2\
saleCons1 ?cons3
?salec3\
saleProd1 ?prod1
?salep1\
saleProd1 ?prod2
?salep2\
saleProd1 ?prod3
?salep3\
totalSales1 ?totalSales
Comment:
Calculates the total sales by producer and by consumer.
----------------------------------------------------------------------
Rule: initialise select prod for first day (initialising)
Antecedents:
and
backSelProd price1
?listSel\
clauseList ?cons
listSelProd1 [?listSel]
Consequents:
?cons
Comment:
Writes in the clause listSelProd1 the list of producers ordered in
accordance to the value of their prices at time 1. This will be used by a
consumer to pick up the producer it will order from and for determining the
amplitude of the interval for prices.
----------------------------------------------------------------------
Rule: initializing choices1 (initializing)
Antecedents:
and
listProd ?list\
= ?list [?p1 ?p2 ?p3]\
(or
= ?choice [?p2
?p3 ?p1]\
= ?choice [?p2
?p3 ?p2]\
= ?choice [?p2
?p1 ?p1]\
= ?choice [?p2
?p1 ?p2]\
= ?choice [?p3
?p3 ?p1]\
= ?choice [?p3
?p3 ?p2]\
= ?choice [?p3
?p1 ?p1]\
= ?choice [?p3
?p1 ?p2])
Consequents:
and
choices1 ?choice
Comment:
Places the different alternatives for the different random choices
of producers for price-setting. (those
are not the choices at time 1)
----------------------------------------------------------------------
Rule: initialSelProd (initializing)
Antecedents:
listProd ?listProd
Consequents:
listChoiceProd1 ?listProd
Comment:
Gives the list of producers ordered in accordance to their price
at time 1
----------------------------------------------------------------------
Rule: list NAMES prices, dependencies among prices ... (initializing)
Antecedents:
and
= ?listNameTotalSales
[totalSales1 totalSales2 totalSales3 totalSales4 totalSales5 totalSales6
totalSales7 totalSales8 totalSales9 totalSales10]\
= ?listNamePrices
[price1 price2 price3 price4 price5 price6 price7 price8 price9 price10]\
= ?listNameListSelProd
[listSelProd1 listSelProd2 listSelProd3 listSelProd4 listSelProd5 listSelProd6
listSelProd7 listSelProd8 listSelProd9 listSelProd10]\
= ?listNameLevel
[level1 level2 level3 level4 level5 level6 level7 level8 level9 level10]\
= ?listNameOrder
[order1 order2 order3 order4 order5 order6 order7 order8 order9 order10]\
= ?listNameOrderProd
[orderProd1 orderProd2 orderProd3 orderProd4 orderProd5 orderProd6 orderProd7
orderProd8 orderProd9 orderProd10]\
= ?listNameOrderCons
[orderCons1 orderCons2 orderCons3 orderCons4 orderCons5 orderCons6 orderCons7
orderCons8 orderCons9 orderCons10]\
= ?listNameDemand
[demand1 demand2 demand3 demand4 demand5 demand6 demand7 demand8 demand9
demand10]\
= ?listNameSales [sale1
sale2 sale3 sale4 sale5 sale6 sale7 sale8 sale9 sale10]\
= ?listNameSalesProd
[saleProd1 saleProd2 saleProd3 saleProd4 saleProd5 saleProd6 saleProd7
saleProd8 saleProd9 saleProd10]\
= ?listNameSalesCons
[saleCons1 saleCons2 saleCons3 saleCons4 saleCons5 saleCons6 saleCons7
saleCons8 saleCons9 saleCons10]\
=
?listNameProductionDay [productionDay1 productionDay2 productionDay3
productionDay4 productionDay5 productionDay6 productionDay7 productionDay8
productionDay9 productionDay10]\
= ?listNameListChoice
[listChoiceProd1 listChoiceProd2 listChoiceProd3 listChoiceProd4
listChoiceProd5 listChoiceProd6 listChoiceProd7 listChoiceProd8 listChoiceProd9
listChoiceProd10]
Consequents:
and
listNameTotalSales
?listNameTotalSales\
listNameSalesCons
?listNameSalesCons\
listNameSalesProd
?listNameSalesProd\
listNamePrices
?listNamePrices\
listNameListSelProd
?listNameListSelProd\
listNameLevel
?listNameLevel\
listNameOrder
?listNameOrder\
listNameOrderCons
?listNameOrderCons\
listNameOrderProd
?listNameOrderProd\
listNameDemand
?listNameDemand\
listNameSales
?listNameSales\
listNameProductionDay
?listNameProductionDay\
listNameListChoice
?listNameListChoice
Comment:
This rule is very useful for meta, as it gives a list of the
predicates to be used (to instantiate as explicitly data like prices, sales,
orders …
In this model rather that having the predicate ‘price’ only and
indicating the time (1, 2, …) as a field in the predicate, it is aggregate to
the name of the predicate, and so will be more specific.
----------------------------------------------------------------------
Rule: minimumPrice (parameters)
Antecedents:
and
iPrice ?initialPrice\
factorMinimumPrice
?fMP\
is ?minimumPrice
?initialPrice * ?fMP
Consequents:
minimumPrice ?minimumPrice
Consumer:
MinimumPrice will be the minimum price any producer can sell its
good. It can be said that minimum price is the production cost of the good.
----------------------------------------------------------------------
Rule: number of consumers, etc. (parameters)
Antecedents:
true
Consequents:
and
noOfConsumers 3\
noOfProducers 3\
noOfStores 1\
noOfFactories 1
Commment:
Indicates the number of consumers and Producer to be created in
the model.
Also it indicate how many factories and Stores a producer has.
----------------------------------------------------------------------
Rule: numbers of simulation days (simulation, start, end)
Antecedents:
true
Consequents:
noOfDays 6
Comment:
This rule indicates the number of iterations (called days) the
simulation will be run
List
of Backward-chaining Rules:
In SDML a clause can be defined as backward-chaining. A
backward-chaining clause works as a ‘database’ with several several
backward-chaining rules to generate the output of the clause. This is seen
below. In the next list of backward-chaining clauses, the name of the clause
appears after the word ‘definition’. The category of the clause is placed in
parenthesis.
All backward-chaining rules but that responsible for building the
theorem in meta have only one rule.
----------------------------------------------------------------------
Rulebase: definition backSelProd (Calculations)
Rule: rule
Antecedents:
and
listProd ?listProd\
= ?listProd [?prod1
?prod2 ?prod3]\
clauseList ?NP1
?nameprice [?prod1 ?price1]\
clauseList ?NP2
?nameprice [?prod2 ?price2]\
clauseList ?NP3
?nameprice [?prod3 ?price3]\
?NP1\
?NP2\
?NP3\
(or
(and
less
?price1 ?price2\
less
?price1 ?price3\
= ?prodsel
?prod1\
(or
(and
less
?price2 ?price3\
=
?prodsel1 ?prod2\
=
?prodsel2 ?prod3)\
(and
(or
less
?price3 ?price2\
=
?price3 ?price2)\
=
?prodsel1 ?prod3\
=
?prodsel2 ?prod2)))\
(and
less
?price2 ?price1\
less
?price2 ?price3\
= ?prodsel
?prod2\
(or
(and
less
?price1 ?price3\
=
?prodsel1 ?prod1\
=
?prodsel2 ?prod3)\
(and
(or
less
?price3 ?price1\
=
?price3 ?price1)\
=
?prodsel1 ?prod3\
=
?prodsel2 ?prod1)))\
(and
less
?price3 ?price2\
less
?price3 ?price1\
= ?prodsel
?prod3\
(or
(and
less
?price1 ?price2\
=
?prodsel1 ?prod1\
=
?prodsel2 ?prod2)\
(and
(or
less
?price2 ?price1\
=
?price2 ?price1)\
=
?prodsel1 ?prod2\
=
?prodsel2 ?prod1)))\
(and
= ?price1 ?price2\
less
?price1 ?price3\
= ?prodsel
?prod1\
= ?prodsel1
?prod2\
= ?prodsel2
?prod3)\
(and
= ?price1
?price3\
less
?price1 ?price2\
= ?prodsel
?prod1\
= ?prodsel1
?prod3\
= ?prodsel2
?prod2)\
(and
= ?price2
?price3\
less
?price2 ?price1\
= ?prodsel
?prod2\
= ?prodsel1
?prod3\
= ?prodsel2
?prod1)\
(and
= ?price2
?price3\
= ?price2
?price1\
= ?prodsel
?prod2\
= ?prodsel1
?prod1\
= ?prodsel2
?prod3))\
= ?listSel [?prodsel
?prodsel1 ?prodsel2]
Consequents:
backSelProd ?nameprice ?listSel
Comment:
This rule gives the name predicate names of producers’ in the list
?listSel in order of value for certain iteration. It gets as input the names of
predicate of prices corresponding to that iteration in the variable ?nameprice.
For example, if the variable has ‘price3’, then prices to be compared are the
prices for iteration 3. This name is used to build the clause to instantiate
prices. E.g.; clauseList ?NP1 ?nameprice [?prod1 ?price1]\
would build the clause to instantiate price3 of producer 1 and the
value would be placed in ?price1.
The returned list: ?listSel is used by consumers for order-setting
(they order form producer with the lowest price) and for calculating the size
of the interval for prices in theorem-checking.
----------------------------------------------------------------------
Rulebase: definition calcDemand (Calculations)
Rule: rule
Antecedents:
and
noOfDays ?noD\
= ?list [?nt]\
demandRange ?min ?max\
is ?media ?min + (?max
- ?min) / 2\
is ?newD (?media +
?media * 0.5 * ((?nt - 1) / (?noD - 1))) * 0.8\
truncated ?nD ?newD
Consequents:
calcDemand ?nD ?list
Comment:
This rule does some numerical manipulations when calculating
demand.
This particular way of calculating demand is not relevant for the
methodology.
----------------------------------------------------------------------
Rulebase: definition calcNewOrder (Calculations)
Rule: rule
Antecedents:
or
(and
= ?producer
?prodsel\
= ?neworder
?demandDay)\
(and
notInferred
= ?producer
?prodsel\
= ?neworder 0)
Consequents:
calcNewOrder ?producer ?prodsel ?demandDay ?neworder
Comment:
This rule performs some numerical manipulation for calculating
consumers’ order. Orders are set to zero expect that to producer with the
lowest price (?prodsel)
----------------------------------------------------------------------
Rulebase: definition calcprice (Calculations)
Rule: calculating delta price
Antecedents:
and
= ?listdata [?oldprice
?otherprice ?mysales ?totalSales]\
is ?mediasales
?totalSales / 3\
is ?difsales ?mysales -
?mediasales\
factorDeltaPrice
?factorDeltaPrice\
is ?difprices
(?otherprice - ?oldprice) * ?factorDeltaPrice\
absoluteValue
?absdifprice ?difprices\
(or
(and
greater
?difsales 0\
is ?pprice
?oldprice + ?absdifprice)\
(and
less
?difsales 0\
is ?pprice
?oldprice - ?absdifprice)\
(and
= ?difsales
0\
is ?pprice
?oldprice))\
minimumPrice ?mP\
(or
(and
(or
=
?pprice ?mP\
less
?pprice ?mP)\
= ?price
?mP)\
(and
greater
?pprice ?mP\
= ?price
?pprice))\
errorFactor ?a\
is ?milllionprice
?price * ?a\
rounded
?millionpureprice ?milllionprice\
is ?cleanedprice
?millionpureprice / ?a
Consequents:
calcprice ?cleanedprice ?listdata
Comment:
This clause is responsible for calculating price. The list input
given in the variable ?lisdata contain the prices and sales necessary for this
task. Then price is returned in ?cleanedprice. Round error is controlled
rounding the lest significant digits of the float point number in the variable
?price. That is made using the inverse of the small number considered as cero
kept in the clause ‘errorFactor’.
----------------------------------------------------------------------
Rulebase: definition calcProductionDay (Calculations)
Rule: rule
Antecedents:
and
is ?prod2
?orderProdToday / ?delay\
truncated ?prod1
?prod2\
is ?limitStore
?capacity - ?levelInValue\
is ?min1 ?maxCapacity /
4\
truncated ?min ?min1\
min ?prodDay1 ?prod1
?maxCapacity ?limitStore\
max
?productionDayOutValue ?min ?prodDay1
Consequents:
calcProductionDay ?orderProdToday ?delay ?capacity ?levelInValue
?maxCapacity ?productionDayOutValue
Comment:
This rule does numerical manipulations necessary for
Production-setting are placed here.
----------------------------------------------------------------------
Rulebase: definition calcSale (Calculations)
Rule: rule
Antecedents:
and
(or
(and
=
?orderProd 0\
= ?per 0)\
(and
greater
?orderProd 0\
is ?per
?orderConsProd / ?orderProd))\
(or
(and
greater
?levelStore ?orderProd\
= ?sale
?orderConsProd)\
(and
(or
less
?levelStore ?orderProd\
=
?levelStore ?orderProd)\
is ?apsale
?levelStore * ?per\
truncated
?sale ?apsale))
Consequents:
calcSale ?levelStore ?orderProd ?orderConsProd ?sale
Comment:
This rule does numerical manipulations necessary for sale-setting
are done using this rule.
----------------------------------------------------------------------
Rulebase: definition otherPrice (Calculations)
Rule: taking the other price
Antecedents:
and
listProd ?listProd\
index ?listProd ?index
?myself\
index ?choiceProd
?index ?mychoice\
clauseList ?priceInsC
?priceIn [?mychoice ?otherprice]\
?priceInsC
Consequents:
otherPrice ?otherprice ?choiceProd ?priceIn ?myself
Comment:
This rule is used to get the price of a chosen producer. Two list
are used: the original list of producers ?listProd, and the list of chosen
producers ?choiceProd, for certain iteration. The producer in position (index)
i of the second list (?choiceProd) is the chosen producer by producer i (that
in position i in the list of ?listProd). This is indicate by using the variable
?index. The position of a producer in ?listProd is taken in this index and then
this value is used to take the corresponding element from the list ?choiceProd.
The correspondent clause for instantiating price is built and then used. The
searched price is output in the variable ?otherprice.
----------------------------------------------------------------------
Rulebase: definition getClauseName (Calculations)
Rule: rule
Antecedents:
and
clauseList ?knowlistC
?knowlistname [?knowlist]\
?knowlistC\
index ?knowlist ?index
?know\
clauseList
?unknownlistC ?unknownlistname [?unknownlist]\
?unknownlistC\
index ?unknownlist
?index ?unknown
Consequents:
getClauseName ?know ?knowlistname ?unknown ?unknownlistname
Comment:
As list of predicate names are built in accordance to the
iteration the data will be valid. E.g., considering lists for prices and sales:
[price1 price2 …] and [sale1 sale2 ..], elements in position i in different
lists correspond to data valid for the same iteration. Given a predicate name
we could find its position in the list it has been place and then other
predicate names corresponding to data valid at the same iteration can be found.
That is the task of this rule. Given the predicate ?know in the list of
predicates ?knowlistname, then the predicate in the same position (?index) in
the list ?unknownlistname is found and placed in returned in the variable
?unknown.
This rule is used by rule in the backward-chaining clause
amIntPrice (listed below).
----------------------------------------------------------------------
Rulebase: definition amIntPrice (prover)
Rule: back
Antecedents:
and
getClauseName
?nameprice listNamePrices ?nameListSelProd listNameListSelProd\
clauseList
?listSelProdC ?nameListSelProd [?listSelProd]\
?listSelProdC\
= ?listSelProd
[?prodsel1 ?prodsel2 ?prodsel3]\
clauseList ?priceC1
?nameprice [?prodsel1 ?price1]\
?priceC1\
clauseList ?priceC3
?nameprice [?prodsel3 ?price3]\
?priceC3\
is ?dif ?price3 -
?price1
Consequents:
amIntPrice ?nameprice ?dif
Comment:
This rule is responsible for calculating the amplitude of the
interval of prices for certain day (iteration). The input is the name of the
predicate of prices, input in the variable ?nameprice. E. g., if the predicate
‘price3’ is given as input (in ?nameprice) then clauses to instantiate the
higher and the lowest price are build using information from the list
?listSelProd, which contains the producer name predicates (producer-1, ..)
ordered in accordance to the value of price. Clause to instantiate the required
prices are build and then used. The value of the difference is returned in the
variable ?dif.
These are the rules to write automatically at prover the
transition rules.
Rulebase: proving (n)>MetaProver (content)
----------------------------------------------------------------------
Rule: writing checkTheorem (building transition rules)
Antecedents:
and
listProd ?list\
= ?list [?prod1 ?prod2
?prod3]\
noOfDays ?noDays\
listNamePrices
?listNamePrices\
subList
?actualListPrices ?listNamePrices 1 ?noDays\
backBuiltTheorem
?actualListPrices ?antList\
clauseList ?antecedent
and ?antList\
namedInstance
?ruletheorem RuleName ‘checkTheorem’
Consequents:
rule ?ruletheorem ?antecedent false
Comment:
Rule for writing the theorem at ‘prover’. It first collects
necessary information from the database to build the theorem:
1. data collection:
Producer's names in the variables: ?prod1, ?prod2, ?prod3
Total number of simulation days in: ?noDays
The list of price predicate names ?listNamePrices (e.g, it
contains, price1, price2, ......pricen, where n is the number of days the
simulation is run). As this list could be kept fixed while noDays is changed in
different experiments, the sublist of predicate names relevant in accordance to
noDays in a experiment is taken in the variable ?actualListPries:
subList ?actualListPrices ?listNamePrices 1 ?noDays\
Then a backward-chaining rule is called to build the antecedent of
the theorem:
backBuiltTheorem ?actualListPrices ?antList\
This rule gets as input the list of price predicates names and
outputs a list of clause to build in the antecedent of the rule in: ?antList
2. building clauses to make up the rule:
Then the antecedent is built, using the clause ‘clauseList’, as
the disjunction of the clause elements of the list ‘?antList’ (this is
indicated by the second element of the clause: ‘and’). The antecedent is called
‘antecedent’.
clauseList ?antecedent and ?antList\
The name of the rules is generated using namedInstance:
namedInstance ?ruletheorem RuleName ‘checkTheorem’
The instance created is called ‘checkTheorem’ is of type RuleName
and has been placed in the variable ?ruletheorem
3. Finally the rule is created in the consequent:
rule ?ruletheorem ?antecedent false/
The name of the clause used to write the rule is ‘rule’. There can
be seen as the elements this clause uses: name of the theorem, the antecedent
of rule and the consequent of the rule (false).
----------------------------------------------------------------------
Rule: writing Choices-Iter (building transition rules)
Antecedents:
and
noOfDays ?nDays\
listNameListChoice ?listNameListChoice\
inInterval ?index 2
?nDays\
index
?listNameListChoice ?index ?choiceName\
is ?previous ?index -
1\
index
?listNameListChoice ?previous ?choiceNamePrevious\
clauseList
?previousChoiceC ?choiceNamePrevious [?previousChoice]\
clauseList ?choicesC
choices1 [?allchoices]\
clauseList ?rChC
randomChoice [?randchoice ?allchoices ?index ?choicesC]\
clauseList ?ant and
[?previousChoiceC ?rChC]\
clauseList ?cons
?choiceName [?randchoice]\
generatedInstance
?ruleChoices RuleName ‘Choices-Iter’ ?index
Consequents:
rule ?ruleChoices ?ant ?cons
Comment:
This rule is responsible for splitting and writing at prover rules
for making producer (traders)'s choices for price-setting.
To figure out how meta write rules at prover, this rule in particular
will be explained in more detail:
1. First data is brought from the rulebase and auxiliary variables
are generated:
a) Number of simulation days: noOfDays ?nDays\
b) Choices predicate names for each day, e.g., choice1, choice2,
... which are in a list whose clause is called listNameListChoice are brought:
listNameListChoice ?listNameListChoice\
c) Then ?index is create as a variable keeping the integers from 2
to the number of simulation days: inInterval
?index 2 ?nDays\
An auxiliary index is defined as index minus one:
is ?previous ?index - 1\
These two indexes are used as pointers to the names of choices in
the list kept in the variable ?listNamListChoice. There will be a rule for each
name in the list, e.g., there will be a rule for each iteration (day) from one
to number of days.
The rules written at prover will generate choices one at a time
(so that the program backtracks for one at a time) -a different assumption is
will be set for each choice. For this, the rule to make the choice for day-i,
to be written in module ‘prove’, will instantiate the choice for the previous
day-(i-1) (there will be dependency among every two rules). While the variable
?index is used to take the name of the predicate of choice for the day the rule
will give the choice (e.g., choice-i; if ?index is at i), the variable
?previous is used to take the name of the choice predicate for the previous day
and will be used to instantiate it.
index ?listNameListChoice ?index ?choiceName\
Takes in ?choiceName the name of the predicate with index ?index
(2, ...noOfDays)(e.g, choice3)
index ?listNameListChoice ?previous ?choiceNamePrevious\
Takes in ?choiceNamePrevious the name of the previous choice
(e.g., choice 2)
2. Then clause are written .. two to be used in the antecedent of
the rule directly (?previousChoiceC and ?rChC) and other (?choiceC) to be used
inside other clause (?rChC).
a) clauseList ?previousChoiceC ?choiceNamePrevious
[?previousChoice]\
This clause builds a clause, in the varible ?previousChoiceC, for
instantiating the previous choice.
b) clauseList ?choicesC choices1 [?allchoices]\
This build a chause to instantiate choices of producers which name
?choiceC (the list of choice of producers are in the dababase under the clause
‘choices1’, so the variable ?allchoices will instantiate the choices when the
clause is used.
c) clauseList ?rChC randomChoice [?randchoice ?allchoices ?index
?choicesC]\
This build a clasue for doing the random choice (notice that the
choice will be taken from those lists instantiates in ?allchoices, which is in
the clause ?choicesC. The name of the variable containing the clause is ?rChC.
The choice will be placed in the variable ?randchoice.
d) clauseList ?ant and [?previousChoiceC ?rChC]\
The antecedent of the rules is built as the disjunction of two
clasues built above: those given by the variables ?previousChoiceC and ?rChC.
The consequent clause has name ?ant
e) clauseList ?cons ?choiceName [?randchoice]\
The consequent of the rules is built. It is given as the choice
given in ?randChoice and the name of the predicate is written is in the
variable ?choiceName
f) generatedInstance ?ruleChoices RuleName ‘Choices-Iter’ ?index
Finally the name of the rules is build with ‘sub-index’ determined
by ?index
3) Finally, the rules are written (by the consequent) with name in
the varible ?ruleChoices, antecedent in ?and and consequent in ?cons:
rule ?ruleChoices ?ant ?cons
----------------------------------------------------------------------
Rule: writing Data-OrderProd-OrderCons (building transition rules)
Antecedents:
and
listCons ?listCons\
= ?listCons [?cons1
?cons2 ?cons3]\
listProd ?listProd\
= ?listProd [?prod1
?prod2 ?prod3]\
noOfDays ?nDays\
inInterval ?index 2
?nDays\
listNameOrder
?listNameOrder\
listNameOrderProd
?listNameOrderProd\
listNameOrderCons
?listNameOrderCons\
index ?listNameOrder
?index ?orderName\
index
?listNameOrderProd ?index ?orderProdName\
index
?listNameOrderCons ?index ?orderConsName\
clauseList ?order11
?orderName [?cons1 ?prod1 ?s1]\
clauseList ?order21
?orderName [?cons2 ?prod1 ?s2]\
clauseList ?order31
?orderName [?cons3 ?prod1 ?s3]\
clauseList ?order12
?orderName [?cons1 ?prod2 ?s4]\
clauseList ?order22
?orderName [?cons2 ?prod2 ?s5]\
clauseList ?order32
?orderName [?cons3 ?prod2 ?s6]\
clauseList ?order13
?orderName [?cons1 ?prod3 ?s7]\
clauseList ?order23
?orderName [?cons2 ?prod3 ?s8]\
clauseList ?order33
?orderName [?cons3 ?prod3 ?s9]\
clauseList ?is1 is
[?order1 ?s1 + ?s4 + ?s7]\
clauseList ?is2 is
[?order2 ?s2 + ?s5 + ?s8]\
clauseList ?is3 is
[?order3 ?s3 + ?s6 + ?s9]\
clauseList ?is4 is
[?orderp1 ?s1 + ?s2 + ?s3]\
clauseList ?is5 is
[?orderp2 ?s4 + ?s5 + ?s6]\
clauseList ?is6 is
[?orderp3 ?s7 + ?s8 + ?s9]\
clauseList ?antecedents
and [?order11 ?order21 ?order31 ?order12 ?order22 ?order32 ?order13 ?order23
?order33 ?is1 ?is2 ?is3 ?is4 ?is5 ?is6]\
clauseList ?conseq1
?orderConsName [?cons1 ?order1]\
clauseList ?conseq2
?orderConsName [?cons2 ?order2]\
clauseList ?conseq3
?orderConsName [?cons3 ?order3]\
clauseList ?conseq4
?orderProdName [?prod1 ?orderp1]\
clauseList ?conseq5
?orderProdName [?prod2 ?orderp2]\
clauseList ?conseq6
?orderProdName [?prod3 ?orderp3]\
clauseList ?consequents
and [?conseq1 ?conseq2 ?conseq3 ?conseq4 ?conseq5 ?conseq6]\
generatedInstance
?rulename RuleName ‘Data-OrderProd-OrderCons’ ?index
Consequents:
rule ?rulename ?antecedents ?consequents
Comment:
This rule split and write the rules for calculating consumer
(distributors) orders and total of orders by consumer and producer.
----------------------------------------------------------------------
Rule: writing Data-SaleProd-OrderCons (building transition rules)
Antecedents:
and
listCons ?listCons\
= ?listCons [?cons1
?cons2 ?cons3]\
listProd ?listProd\
= ?listProd [?prod1
?prod2 ?prod3]\
noOfDays ?nDays\
inInterval ?index 2
?nDays\
listNameSales
?listNameSales\
listNameSalesProd
?listNameSalesProd\
listNameSalesCons
?listNameSalesCons\
listNameTotalSales
?listNameTotalSales\
index ?listNameSales
?index ?salesName\
index ?listNameSalesProd
?index ?salesProdName\
index
?listNameSalesCons ?index ?salesConsName\
index
?listNameTotalSales ?index ?nameTotalSales\
clauseList ?sales11
?salesName [?prod1 ?cons1 ?s1]\
clauseList ?sales21
?salesName [?prod1 ?cons2 ?s2]\
clauseList ?sales31
?salesName [?prod1 ?cons3 ?s3]\
clauseList ?sales12
?salesName [?prod2 ?cons1 ?s4]\
clauseList ?sales22
?salesName [?prod2 ?cons2 ?s5]\
clauseList ?sales32
?salesName [?prod2 ?cons3 ?s6]\
clauseList ?sales13
?salesName [?prod3 ?cons1 ?s7]\
clauseList ?sales23
?salesName [?prod3 ?cons2 ?s8]\
clauseList ?sales33
?salesName [?prod3 ?cons3 ?s9]\
clauseList ?is1 is
[?salesc1 ?s1 + ?s4 + ?s7]\
clauseList ?is2 is
[?salesc2 ?s2 + ?s5 + ?s8]\
clauseList ?is3 is
[?salesc3 ?s3 + ?s6 + ?s9]\
clauseList ?is4 is
[?salesp1 ?s1 + ?s2 + ?s3]\
clauseList ?is5 is
[?salesp2 ?s4 + ?s5 + ?s6]\
clauseList ?is6 is
[?salesp3 ?s7 + ?s8 + ?s9]\
clauseList ?is7 is
[?totalSales ?salesc1 + ?salesc2 + ?salesc3]\
clauseList ?antecedents
and [?sales11 ?sales21 ?sales31 ?sales12 ?sales22 ?sales32 ?sales13 ?sales23
?sales33 ?is1 ?is2 ?is3 ?is4 ?is5 ?is6 ?is7]\
clauseList ?conseq1
?salesConsName [?cons1 ?salesc1]\
clauseList ?conseq2
?salesConsName [?cons2 ?salesc2]\
clauseList ?conseq3
?salesConsName [?cons3 ?salesc3]\
clauseList ?conseq4
?salesProdName [?prod1 ?salesp1]\
clauseList ?conseq5
?salesProdName [?prod2 ?salesp2]\
clauseList ?conseq6
?salesProdName [?prod3 ?salesp3]\
clauseList ?conseq7
?nameTotalSales [?totalSales]\
clauseList ?consequents
and [?conseq1 ?conseq2 ?conseq3 ?conseq4 ?conseq5 ?conseq6 ?conseq7]\
generatedInstance
?rulename RuleName ‘Data-SalesProd-OrderCons’ ?index
Consequents:
rule ?rulename ?antecedents ?consequents
Comment:
This rule is responsible for splitting and writing rules for
calculating sales, and total sales by consumer and producer.
----------------------------------------------------------------------
Rule: writing Data-SelProd (building transition rules)
Antecedents:
and
listProd ?list\
= ?list [?prod1 ?prod2
?prod3]\
listNamePrices ?listpr\
noOfDays ?noDays\
inInterval ?index 2
?noDays\
index ?listpr ?index
?nameprice\
listNameListSelProd
?listNameListSelProd\
index
?listNameListSelProd ?index ?namesel\
clauseList ?getSelProdC
backSelProd [?nameprice ?listSel]\
clauseList ?cons
?namesel [?listSel]\
generatedInstance
?ruleSelProd RuleName ‘Data-SelProd’ ?nameprice
Consequents:
rule ?ruleSelProd ?getSelProdC ?cons
Comment:
This rule split and write the rule to order producers in
accordance to their price .. the result of these rules will be useful for
determining size of the interval of prices at each day and that producer with
the lowest prices which is chosen by consumers to place their orders at.
----------------------------------------------------------------------
Rule: writing TR-Demand-and-Order (building transition rules)
Antecedents:
and
noOfDays ?nDays\
listNameDemand
?listNameDemands\
inInterval ?index 2
?nDays\
index ?listNameDemands
?index ?demandOut\
is ?previous ?index -
1\
index ?listNameDemands
?previous ?demandIn\
calcDemand ?demandDay
[?index]\
listNameOrder
?listNameOrder\
listNameSales
?listNameSales\
listNameSalesCons
?listNameSalesCons\
listNameListSelProd
?listNameListSelProd\
index ?listNameOrder
?previous ?orderIn\
index ?listNameOrder
?index ?orderOut\
index ?listNameSales
?previous ?namesale\
index
?listNameSalesCons ?previous ?namesalescons\
index
?listNameListSelProd ?index ?namelistselprod\
clauseList
?dataDemandIn ?demandIn [?cons ?olddemand]\
clauseList ?oldSaleC
?namesale [?prod ?cons ?oldsalevalue]\
clauseList
?oldSaleConsC ?namesalescons [?cons ?oldsaleconsvalue]\
clauseList ?firstprodC
?namelistselprod [[?prodsel ?other1 ?other2]]\
clauseList ?oldOrderC
?orderIn [?cons ?prod ?oldordervalue]\
clauseList ?isC is
[?newdemand ?olddemand + ?demandDay - ?oldsaleconsvalue]\
clauseList ?neworderC
calcNewOrder [?prod ?prodsel ?demandDay ?newordervalue]\
clauseList ?isC1 is
[?neworder ?oldordervalue + ?newordervalue - ?oldsalevalue]\
clauseList ?antecedents
and [?dataDemandIn ?oldSaleC ?oldSaleConsC ?firstprodC ?oldOrderC ?isC
?neworderC ?isC1]\
clauseList ?cons1
?demandOut [?cons ?newdemand]\
clauseList ?cons2
?orderOut [?cons ?prod ?neworder]\
clauseList ?consequents
and [?cons1 ?cons2]\
generatedInstance
?rulename RuleName ‘TR-Demand-and-Order’ ?demandIn
Consequents:
rule ?rulename ?antecedents ?consequents
Comment:
This rule split and write at prover the rule for calculating
demand and order for each iteration. If the data the rule needs from previous
iterations is well known then the rule can also be split other variables, e.g.,
the producer or consumer. E.g., when calculating a new level of demand for
consumer-i, that level depends on consumer-i's demand in the previous day. So a
rule could be written more specifically for each consumer.
----------------------------------------------------------------------
Rule: writing TR-Price (building transition rules)
Antecedents:
and
noOfDays ?nDays\
inInterval ?index 2
?nDays\
is ?previous ?index -
1\
listNamePrices
?listNamePrices\
listNameListChoice
?listNameListChoice\
index ?listNamePrices
?index ?priceOut\
index ?listNamePrices
?previous ?priceIn\
index
?listNameListChoice ?index ?choicesNameList\
listNameSalesProd
?listNameSalesProd\
index ?listNameSalesProd
?previous ?nameSalesProd\
listNameTotalSales
?listNameTotalSales\
index
?listNameTotalSales ?previous ?nameTotalSales\
clauseList
?clauseSalesProd ?nameSalesProd [?prod ?mysales]\
clauseList
?clauseTotalSales ?nameTotalSales [?totalSales]\
clauseList ?dataPriceIn
?priceIn [?prod ?oldprice]\
clauseList ?choices1C
?choicesNameList [?choices]\
clauseList ?eq1C =
[?choices [?sel1 ?sel2 ?sel3]]\
clauseList ?dataPriceIn
?priceIn [?prod ?oldprice]\
clauseList ?otherpriceC
otherPrice [?otherprice ?choices ?priceIn ?prod]\
clauseList ?calcPriceC
calcprice [?newprice [?oldprice ?otherprice ?mysales ?totalSales]]\
clauseList ?ant and
[?clauseSalesProd ?clauseTotalSales ?dataPriceIn ?choices1C ?eq1C ?otherpriceC
?calcPriceC]\
clauseList ?cons
?priceOut [?prod ?newprice]\
generatedInstance
?rulename RuleName ‘TR-Price’ ?priceIn
Consequents:
rule ?rulename ?ant ?cons
Comment:
Splits and writes transition rules for calculating prices.
----------------------------------------------------------------------
Rule: writing TR-ProductionDay-and-Level (building transition
rules)
Antecedents:
and
producer ?prod\
store ?store\
factory ?factory\
storeOwner ?store
?prod\
capacityStore ?store
?capacity\
factoryOwner ?factory
?prod\
delay ?factory ?delay\
noOfDays ?nDays\
inInterval ?index 2
?nDays\
is ?previous ?index -
1\
maxCapacity ?factory
?maxCapacity\
listNameLevel
?listNameLevel\
listNameProductionDay
?listNameProductionDay\
listNameSalesProd
?listNameSalesProd\
listNameOrderProd ?listNameOrderProd\
index ?listNameLevel
?index ?levelOut\
index
?listNameProductionDay ?index ?productionDayOut\
index ?listNameLevel
?previous ?levelIn\
index
?listNameProductionDay ?previous ?productionDayIn\
index
?listNameSalesProd ?previous ?salesProdIn\
index
?listNameOrderProd ?index ?orderProd\
clauseList ?levelInC
?levelIn [?store ?levelInValue]\
clauseList
?salesProdInC ?salesProdIn [?prod ?salesProdInValue]\
clauseList ?orderProdC
?orderProd [?prod ?orderProdToday]\
clauseList ?productionDayC
calcProductionDay [?orderProdToday ?delay ?capacity ?levelInValue ?maxCapacity
?productionDayOutValue]\
clauseList ?isLevel is
[?levelOutValue ?levelInValue + ?productionDayOutValue - ?salesProdInValue]\
clauseList ?antecedents
and [?levelInC ?salesProdInC ?orderProdC ?productionDayC ?isLevel]\
clauseList ?consLevel
?levelOut [?store ?levelOutValue]\
clauseList
?consProductionDay ?productionDayOut [?factory ?productionDayOutValue]\
clauseList ?consequents
and [?consLevel ?consProductionDay]\
generatedInstance ?rule
RuleName ‘TR-ProductionDay-and-Level’ ?previous
Consequents:
rule ?rule ?antecedents ?consequents
Comment:
Split the transition rules for calculating a producer's production
at a factory and its level of good at a store
----------------------------------------------------------------------
Rule: writing TR-Sales (building transition rules)
Antecedents:
and
storeOwner ?store
?prod\
consumer ?cons\
producer ?prod\
noOfDays ?nDays\
listNameSales
?listNameSales\
listNameLevel ?listNameLevel\
listNameOrder
?listNameOrder\
listNameOrderProd
?listNameOrderProd\
inInterval ?index 2
?nDays\
index ?listNameSales
?index ?saleOut\
index ?listNameLevel
?index ?levelOut\
index ?listNameOrder
?index ?orderOut\
index ?listNameOrderProd
?index ?orderProdOut\
clauseList ?levelC
?levelOut [?store ?levelStore]\
clauseList ?orderC
?orderOut [?cons ?prod ?orderConsProd]\
clauseList ?orderProdC
?orderProdOut [?prod ?orderProd]\
clauseList ?calSaleC
calcSale [?levelStore ?orderProd ?orderConsProd ?saleValue]\
clauseList ?antecedent
and [?levelC ?orderC ?orderProdC ?calSaleC]\
clauseList ?consequent
?saleOut [?prod ?cons ?saleValue]\
generatedInstance ?rule
RuleName ‘TR-Sales’ ?index
Consequents:
rule ?rule ?antecedent ?consequent
Comment:
This rule is responsible for splitting and writing the transition
rules for calculating producer's sales.
=================================================================
=================================================================
Backward-chaining rule to write up the theorem.
First the rule for the general case, back-rule, is listed. Then
the rule for the basic case (to implement the last recursive call), base, will
be listed.
Rulebase: definition backBuiltTheorem (theorem)
----------------------------------------------------------------------
Rule: back-rule
Antecedents:
and
clauseList ?amIntPrice1 amIntPrice [?nprice1 ?dif1]\
clauseList ?amIntPrice2 amIntPrice [?nprice2 ?dif2]\
clauseList ?greaterC greater [?dif2 ?dif1]\
clauseList ?notInferredC notInferred [?greaterC]\
roundError ?roundError\
clauseList ?isC is [?dif ?dif1 - ?dif2]\
clauseList ?aVC absoluteValue [?absdif ?dif]\
clauseList ?greaterE greater [?absdif ?roundError]\
clauseList ?notInferredE notInferred [?greaterE]\
clauseList ?notInferred or [?notInferredC ?notInferredE]\
backBuiltTheorem [?nprice2 | ?rest] ?antListPost\
Consequents:
backBuiltTheorem [?nprice1
?nprice2 | ?rest] [?amIntPrice1 ?amIntPrice2 ?isC ?aVC ?notInferred |
?antListPost]\
Comment:
This rules calls itself recursively. Its is called to build the
theorem, in this form:
backBuiltTheorem ?actualListPrices ?antList\
A list of names of price predicates (price1, ...) is sent in
?actualListPrices and a list of clauses to build the antecedent of the rules is
returned in ?antList. For each recursive call of the rule a list of clauses to
build part of the rule like the following must be sent (see the theorem in the
rules of prover):
amIntPrice price1 ?_-1\
amIntPrice price3 ?_-2\
is ?_-3 ?_-1 - ?_-2\
absoluteValue ?_-4
?_-3\
(or
notInferred
greater
?_-2 ?_-1\
notInferred
greater
?_-4 1.0e-8)\
This clauses are built using the clause ‘clauseList’ and the three
first names of prices listed in the input (called ?nprice1 ?nprice2 and
?nprice3] (see the first list in the consequent of the rule). The clauses built
are placed in the list to be returned (second list in the predicate) and
concatenated to the results got from the recursive call made at the end of the
list of antecedents. The input to the recursive call of the rule are the two
second price predicate names already used (?price2 ?price3]. The answer from
this recursive call is got in the variable ?antListPost and concatenated, in
the output list (see second list in the consequent)
----------------------------------------------------------------------
Rule: base
Antecedents:
and
clauseList ?amIntPrice1
amIntPrice [?nprice1 ?dif1]\
clauseList ?amIntPrice2
amIntPrice [?nprice2 ?dif2]\
clauseList ?greaterC
greater [?dif2 ?dif1]\
clauseList
?notInferredC notInferred [?greaterC]\
roundError ?roundError\
clauseList ?isC is
[?dif ?dif1 - ?dif2]\
clauseList ?aVC
absoluteValue [?absdif ?dif]\
clauseList ?greaterE
greater [?absdif ?roundError]\
clauseList
?notInferredE notInferred [?greaterE]\
clauseList ?notInferred
or [?notInferredC ?notInferredE]\
= ?listPost
[?amIntPrice1 ?amIntPrice2 ?isC ?aVC ?notInferred]\
Consequents:
backBuiltTheorem [?nprice1 ?nprice2] ?listPost\
Commment:
This rule implements the last recursive call to the rule building
the theorem.
It will fire in case the input list (first list in the call of the
rule, backBuiltTheorem, e.g., the list with name of price predicates) has only
two elements, e.g., there is not ‘rest’.
Rulebase: prover@model.universe (day: 1)
----------------------------------------------------------------------
Rule: checkTheorem (meta-accessible)
Antecedents:
and
amIntPrice price1 ?_-1\
amIntPrice price2 ?_-2\
is ?_-3 ?_-1 - ?_-2\
absoluteValue ?_-4
?_-3\
(or
notInferred
greater
?_-2 ?_-1\
notInferred
greater
?_-4 1.0e-8)\
amIntPrice price2 ?_-5\
amIntPrice price3 ?_-6\
is ?_-7 ?_-5 - ?_-6\
absoluteValue ?_-8
?_-7\
(or
notInferred
greater
?_-6 ?_-5\
notInferred
greater
?_-8 1.0e-8)\
amIntPrice price3 ?_-9\
amIntPrice price4
?_-10\
is ?_-11 ?_-9 - ?_-10\
absoluteValue ?_-12
?_-11\
(or
notInferred
greater
?_-10 ?_-9\
notInferred
greater
?_-12 1.0e-8)\
amIntPrice price4
?_-13\
amIntPrice price5
?_-14\
is ?_-15 ?_-13 - ?_-14\
absoluteValue ?_-16
?_-15\
(or
notInferred
greater
?_-14 ?_-13\
notInferred
greater
?_-16 1.0e-8)\
amIntPrice price5
?_-17\
amIntPrice price6
?_-18\
is ?_-19 ?_-17 - ?_-18\
absoluteValue ?_-20
?_-19\
(or
notInferred
greater
?_-18 ?_-17\
notInferred
greater
?_-20 1.0e-8)\
Consequents:
false
----------------------------------------------------------------------
Rule: Choices-Iter-1 (meta-accessible)
Antecedents:
and
listChoiceProd1
?previousChoice\
randomChoice
?randchoice ?allchoices 2
choices1
?allchoices
Consequents:
listChoiceProd2 ?randchoice
----------------------------------------------------------------------
Rule: Choices-Iter-2 (meta-accessible)
Antecedents:
and
listChoiceProd2
?previousChoice\
randomChoice ?randchoice
?allchoices 3
choices1
?allchoices
Consequents:
listChoiceProd3 ?randchoice
----------------------------------------------------------------------
Rule: Choices-Iter-3 (meta-accessible)
Antecedents:
and
listChoiceProd3
?previousChoice\
randomChoice
?randchoice ?allchoices 4
choices1
?allchoices
Consequents:
listChoiceProd4 ?randchoice
----------------------------------------------------------------------
Rule: Choices-Iter-4 (meta-accessible)
Antecedents:
and
listChoiceProd4
?previousChoice\
randomChoice
?randchoice ?allchoices 5
choices1
?allchoices
Consequents:
listChoiceProd5 ?randchoice
----------------------------------------------------------------------
Rule: Choices-Iter-5 (meta-accessible)
Antecedents:
and
listChoiceProd5
?previousChoice\
randomChoice
?randchoice ?allchoices 6
choices1
?allchoices
Consequents:
listChoiceProd6 ?randchoice
----------------------------------------------------------------------
Rule: Data-OrderProd-OrderCons-1 (meta-accessible)
Antecedents:
and
order2
'consumer-1'@simulation 'producer-1'@simulation ?s1\
order2
'consumer-2'@simulation 'producer-1'@simulation ?s2\
order2
'consumer-3'@simulation 'producer-1'@simulation ?s3\
order2
'consumer-1'@simulation 'producer-2'@simulation ?s4\
order2
'consumer-2'@simulation 'producer-2'@simulation ?s5\
order2
'consumer-3'@simulation 'producer-2'@simulation ?s6\
order2
'consumer-1'@simulation 'producer-3'@simulation ?s7\
order2
'consumer-2'@simulation 'producer-3'@simulation ?s8\
order2 'consumer-3'@simulation
'producer-3'@simulation ?s9\
is ?order1 ?s1 + ?s4 +
?s7\
is ?order2 ?s2 + ?s5 +
?s8\
is ?order3 ?s3 + ?s6 +
?s9\
is ?orderp1 ?s1 + ?s2 +
?s3\
is ?orderp2 ?s4 + ?s5 +
?s6\
is ?orderp3 ?s7 + ?s8 +
?s9
Consequents:
and
orderCons2 'consumer-1'@simulation
?order1\
orderCons2
'consumer-2'@simulation ?order2\
orderCons2
'consumer-3'@simulation ?order3\
orderProd2
'producer-1'@simulation ?orderp1\
orderProd2
'producer-2'@simulation ?orderp2\
orderProd2
'producer-3'@simulation ?orderp3
----------------------------------------------------------------------
Rule: Data-OrderProd-OrderCons-2 (meta-accessible)
Antecedents:
and
order3
'consumer-1'@simulation 'producer-1'@simulation ?s1\
order3
'consumer-2'@simulation 'producer-1'@simulation ?s2\
order3
'consumer-3'@simulation 'producer-1'@simulation ?s3\
order3
'consumer-1'@simulation 'producer-2'@simulation ?s4\
order3
'consumer-2'@simulation 'producer-2'@simulation ?s5\
order3
'consumer-3'@simulation 'producer-2'@simulation ?s6\
order3
'consumer-1'@simulation 'producer-3'@simulation ?s7\
order3
'consumer-2'@simulation 'producer-3'@simulation ?s8\
order3
'consumer-3'@simulation 'producer-3'@simulation ?s9\
is ?order1 ?s1 + ?s4 +
?s7\
is ?order2 ?s2 + ?s5 +
?s8\
is ?order3 ?s3 + ?s6 +
?s9\
is ?orderp1 ?s1 + ?s2 +
?s3\
is ?orderp2 ?s4 + ?s5 +
?s6\
is ?orderp3 ?s7 + ?s8 +
?s9
Consequents:
and
orderCons3
'consumer-1'@simulation ?order1\
orderCons3
'consumer-2'@simulation ?order2\
orderCons3
'consumer-3'@simulation ?order3\
orderProd3
'producer-1'@simulation ?orderp1\
orderProd3
'producer-2'@simulation ?orderp2\
orderProd3
'producer-3'@simulation ?orderp3
----------------------------------------------------------------------
Rule: Data-OrderProd-OrderCons-3 (meta-accessible)
Antecedents:
and
order4
'consumer-1'@simulation 'producer-1'@simulation ?s1\
order4
'consumer-2'@simulation 'producer-1'@simulation ?s2\
order4
'consumer-3'@simulation 'producer-1'@simulation ?s3\
order4
'consumer-1'@simulation 'producer-2'@simulation ?s4\
order4
'consumer-2'@simulation 'producer-2'@simulation ?s5\
order4
'consumer-3'@simulation 'producer-2'@simulation ?s6\
order4
'consumer-1'@simulation 'producer-3'@simulation ?s7\
order4
'consumer-2'@simulation 'producer-3'@simulation ?s8\
order4
'consumer-3'@simulation 'producer-3'@simulation ?s9\
is ?order1 ?s1 + ?s4 +
?s7\
is ?order2 ?s2 + ?s5 +
?s8\
is ?order3 ?s3 + ?s6 +
?s9\
is ?orderp1 ?s1 + ?s2 +
?s3\
is ?orderp2 ?s4 + ?s5 +
?s6\
is ?orderp3 ?s7 + ?s8 +
?s9
Consequents:
and
orderCons4
'consumer-1'@simulation ?order1\
orderCons4
'consumer-2'@simulation ?order2\
orderCons4
'consumer-3'@simulation ?order3\
orderProd4
'producer-1'@simulation ?orderp1\
orderProd4
'producer-2'@simulation ?orderp2\
orderProd4
'producer-3'@simulation ?orderp3
----------------------------------------------------------------------
Rule: Data-OrderProd-OrderCons-4 (meta-accessible)
Antecedents:
and
order5
'consumer-1'@simulation 'producer-1'@simulation ?s1\
order5
'consumer-2'@simulation 'producer-1'@simulation ?s2\
order5
'consumer-3'@simulation 'producer-1'@simulation ?s3\
order5
'consumer-1'@simulation 'producer-2'@simulation ?s4\
order5
'consumer-2'@simulation 'producer-2'@simulation ?s5\
order5
'consumer-3'@simulation 'producer-2'@simulation ?s6\
order5
'consumer-1'@simulation 'producer-3'@simulation ?s7\
order5
'consumer-2'@simulation 'producer-3'@simulation ?s8\
order5
'consumer-3'@simulation 'producer-3'@simulation ?s9\
is ?order1 ?s1 + ?s4 +
?s7\
is ?order2 ?s2 + ?s5 +
?s8\
is ?order3 ?s3 + ?s6 +
?s9\
is ?orderp1 ?s1 + ?s2 +
?s3\
is ?orderp2 ?s4 + ?s5 +
?s6\
is ?orderp3 ?s7 + ?s8 +
?s9
Consequents:
and
orderCons5
'consumer-1'@simulation ?order1\
orderCons5
'consumer-2'@simulation ?order2\
orderCons5
'consumer-3'@simulation ?order3\
orderProd5
'producer-1'@simulation ?orderp1\
orderProd5
'producer-2'@simulation ?orderp2\
orderProd5
'producer-3'@simulation ?orderp3
----------------------------------------------------------------------
Rule: Data-OrderProd-OrderCons-5 (meta-accessible)
Antecedents:
and
order6
'consumer-1'@simulation 'producer-1'@simulation ?s1\
order6
'consumer-2'@simulation 'producer-1'@simulation ?s2\
order6
'consumer-3'@simulation 'producer-1'@simulation ?s3\
order6
'consumer-1'@simulation 'producer-2'@simulation ?s4\
order6
'consumer-2'@simulation 'producer-2'@simulation ?s5\
order6
'consumer-3'@simulation 'producer-2'@simulation ?s6\
order6
'consumer-1'@simulation 'producer-3'@simulation ?s7\
order6
'consumer-2'@simulation 'producer-3'@simulation ?s8\
order6
'consumer-3'@simulation 'producer-3'@simulation ?s9\
is ?order1 ?s1 + ?s4 +
?s7\
is ?order2 ?s2 + ?s5 +
?s8\
is ?order3 ?s3 + ?s6 +
?s9\
is ?orderp1 ?s1 + ?s2 +
?s3\
is ?orderp2 ?s4 + ?s5 +
?s6\
is ?orderp3 ?s7 + ?s8 +
?s9
Consequents:
and
orderCons6
'consumer-1'@simulation ?order1\
orderCons6
'consumer-2'@simulation ?order2\
orderCons6
'consumer-3'@simulation ?order3\
orderProd6
'producer-1'@simulation ?orderp1\
orderProd6
'producer-2'@simulation ?orderp2\
orderProd6
'producer-3'@simulation ?orderp3
----------------------------------------------------------------------
Rule: Data-SalesProd-OrderCons-1 (meta-accessible)
Antecedents:
and
sale2
'producer-1'@simulation 'consumer-1'@simulation ?s1\
sale2
'producer-1'@simulation 'consumer-2'@simulation ?s2\
sale2
'producer-1'@simulation 'consumer-3'@simulation ?s3\
sale2
'producer-2'@simulation 'consumer-1'@simulation ?s4\
sale2
'producer-2'@simulation 'consumer-2'@simulation ?s5\
sale2
'producer-2'@simulation 'consumer-3'@simulation ?s6\
sale2
'producer-3'@simulation 'consumer-1'@simulation ?s7\
sale2
'producer-3'@simulation 'consumer-2'@simulation ?s8\
sale2
'producer-3'@simulation 'consumer-3'@simulation ?s9\
is ?salesc1 ?s1 + ?s4 +
?s7\
is ?salesc2 ?s2 + ?s5 +
?s8\
is ?salesc3 ?s3 + ?s6 +
?s9\
is ?salesp1 ?s1 + ?s2 +
?s3\
is ?salesp2 ?s4 + ?s5 +
?s6\
is ?salesp3 ?s7 + ?s8 +
?s9\
is ?totalSales ?salesc1
+ ?salesc2 + ?salesc3
Consequents:
and
saleCons2
'consumer-1'@simulation ?salesc1\
saleCons2
'consumer-2'@simulation ?salesc2\
saleCons2
'consumer-3'@simulation ?salesc3\
saleProd2
'producer-1'@simulation ?salesp1\
saleProd2
'producer-2'@simulation ?salesp2\
saleProd2
'producer-3'@simulation ?salesp3\
totalSales2 ?totalSales
----------------------------------------------------------------------
Rule: Data-SalesProd-OrderCons-2 (meta-accessible)
Antecedents:
and
sale3
'producer-1'@simulation 'consumer-1'@simulation ?s1\
sale3
'producer-1'@simulation 'consumer-2'@simulation ?s2\
sale3
'producer-1'@simulation 'consumer-3'@simulation ?s3\
sale3
'producer-2'@simulation 'consumer-1'@simulation ?s4\
sale3
'producer-2'@simulation 'consumer-2'@simulation ?s5\
sale3
'producer-2'@simulation 'consumer-3'@simulation ?s6\
sale3
'producer-3'@simulation 'consumer-1'@simulation ?s7\
sale3
'producer-3'@simulation 'consumer-2'@simulation ?s8\
sale3
'producer-3'@simulation 'consumer-3'@simulation ?s9\
is ?salesc1 ?s1 + ?s4 +
?s7\
is ?salesc2 ?s2 + ?s5 +
?s8\
is ?salesc3 ?s3 + ?s6 +
?s9\
is ?salesp1 ?s1 + ?s2 +
?s3\
is ?salesp2 ?s4 + ?s5 +
?s6\
is ?salesp3 ?s7 + ?s8 +
?s9\
is ?totalSales ?salesc1
+ ?salesc2 + ?salesc3
Consequents:
and
saleCons3
'consumer-1'@simulation ?salesc1\
saleCons3
'consumer-2'@simulation ?salesc2\
saleCons3
'consumer-3'@simulation ?salesc3\
saleProd3
'producer-1'@simulation ?salesp1\
saleProd3
'producer-2'@simulation ?salesp2\
saleProd3
'producer-3'@simulation ?salesp3\
totalSales3 ?totalSales
----------------------------------------------------------------------
Rule: Data-SalesProd-OrderCons-3 (meta-accessible)
Antecedents:
and
sale4
'producer-1'@simulation 'consumer-1'@simulation ?s1\
sale4
'producer-1'@simulation 'consumer-2'@simulation ?s2\
sale4
'producer-1'@simulation 'consumer-3'@simulation ?s3\
sale4
'producer-2'@simulation 'consumer-1'@simulation ?s4\
sale4
'producer-2'@simulation 'consumer-2'@simulation ?s5\
sale4
'producer-2'@simulation 'consumer-3'@simulation ?s6\
sale4
'producer-3'@simulation 'consumer-1'@simulation ?s7\
sale4
'producer-3'@simulation 'consumer-2'@simulation ?s8\
sale4
'producer-3'@simulation 'consumer-3'@simulation ?s9\
is ?salesc1 ?s1 + ?s4 +
?s7\
is ?salesc2 ?s2 + ?s5 +
?s8\
is ?salesc3 ?s3 + ?s6 +
?s9\
is ?salesp1 ?s1 + ?s2 +
?s3\
is ?salesp2 ?s4 + ?s5 +
?s6\
is ?salesp3 ?s7 + ?s8 +
?s9\
is ?totalSales ?salesc1
+ ?salesc2 + ?salesc3
Consequents:
and
saleCons4
'consumer-1'@simulation ?salesc1\
saleCons4
'consumer-2'@simulation ?salesc2\
saleCons4
'consumer-3'@simulation ?salesc3\
saleProd4
'producer-1'@simulation ?salesp1\
saleProd4 'producer-2'@simulation
?salesp2\
saleProd4
'producer-3'@simulation ?salesp3\
totalSales4 ?totalSales
----------------------------------------------------------------------
Rule: Data-SalesProd-OrderCons-4 (meta-accessible)
Antecedents:
and
sale5 'producer-1'@simulation
'consumer-1'@simulation ?s1\
sale5
'producer-1'@simulation 'consumer-2'@simulation ?s2\
sale5
'producer-1'@simulation 'consumer-3'@simulation ?s3\
sale5
'producer-2'@simulation 'consumer-1'@simulation ?s4\
sale5
'producer-2'@simulation 'consumer-2'@simulation ?s5\
sale5
'producer-2'@simulation 'consumer-3'@simulation ?s6\
sale5
'producer-3'@simulation 'consumer-1'@simulation ?s7\
sale5
'producer-3'@simulation 'consumer-2'@simulation ?s8\
sale5
'producer-3'@simulation 'consumer-3'@simulation ?s9\
is ?salesc1 ?s1 + ?s4 +
?s7\
is ?salesc2 ?s2 + ?s5 +
?s8\
is ?salesc3 ?s3 + ?s6 +
?s9\
is ?salesp1 ?s1 + ?s2 +
?s3\
is ?salesp2 ?s4 + ?s5 +
?s6\
is ?salesp3 ?s7 + ?s8 +
?s9\
is ?totalSales ?salesc1
+ ?salesc2 + ?salesc3
Consequents:
and
saleCons5
'consumer-1'@simulation ?salesc1\
saleCons5
'consumer-2'@simulation ?salesc2\
saleCons5
'consumer-3'@simulation ?salesc3\
saleProd5
'producer-1'@simulation ?salesp1\
saleProd5
'producer-2'@simulation ?salesp2\
saleProd5
'producer-3'@simulation ?salesp3\
totalSales5 ?totalSales
----------------------------------------------------------------------
Rule: Data-SalesProd-OrderCons-5 (meta-accessible)
Antecedents:
and
sale6
'producer-1'@simulation 'consumer-1'@simulation ?s1\
sale6 'producer-1'@simulation
'consumer-2'@simulation ?s2\
sale6
'producer-1'@simulation 'consumer-3'@simulation ?s3\
sale6
'producer-2'@simulation 'consumer-1'@simulation ?s4\
sale6
'producer-2'@simulation 'consumer-2'@simulation ?s5\
sale6
'producer-2'@simulation 'consumer-3'@simulation ?s6\
sale6
'producer-3'@simulation 'consumer-1'@simulation ?s7\
sale6
'producer-3'@simulation 'consumer-2'@simulation ?s8\
sale6
'producer-3'@simulation 'consumer-3'@simulation ?s9\
is ?salesc1 ?s1 + ?s4 +
?s7\
is ?salesc2 ?s2 + ?s5 +
?s8\
is ?salesc3 ?s3 + ?s6 +
?s9\
is ?salesp1 ?s1 + ?s2 +
?s3\
is ?salesp2 ?s4 + ?s5 +
?s6\
is ?salesp3 ?s7 + ?s8 +
?s9\
is ?totalSales ?salesc1
+ ?salesc2 + ?salesc3
Consequents:
and
saleCons6
'consumer-1'@simulation ?salesc1\
saleCons6
'consumer-2'@simulation ?salesc2\
saleCons6
'consumer-3'@simulation ?salesc3\
saleProd6
'producer-1'@simulation ?salesp1\
saleProd6
'producer-2'@simulation ?salesp2\
saleProd6
'producer-3'@simulation ?salesp3\
totalSales6 ?totalSales
----------------------------------------------------------------------
Rule: Data-SelProd-1 (meta-accessible)
Antecedents:
backSelProd price2 ?listSel
Consequents:
listSelProd2 ?listSel
----------------------------------------------------------------------
Rule: Data-SelProd-2 (meta-accessible)
Antecedents:
backSelProd price3 ?listSel
Consequents:
listSelProd3 ?listSel
----------------------------------------------------------------------
Rule: Data-SelProd-3 (meta-accessible)
Antecedents:
backSelProd price4 ?listSel
Consequents:
listSelProd4 ?listSel
----------------------------------------------------------------------
Rule: Data-SelProd-4 (meta-accessible)
Antecedents:
backSelProd price5 ?listSel
Consequents:
listSelProd5 ?listSel
----------------------------------------------------------------------
Rule: Data-SelProd-5 (meta-accessible)
Antecedents:
backSelProd price6 ?listSel
Consequents:
listSelProd6 ?listSel
----------------------------------------------------------------------
Rule: TR-Demand-and-Order-1 (meta-accessible)
Antecedents:
and
demand1 ?cons
?olddemand\
sale1 ?prod ?cons
?oldsalevalue\
saleCons1 ?cons
?oldsaleconsvalue\
listSelProd2 [?prodsel
?other1 ?other2]\
order1 ?cons ?prod
?oldordervalue\
is ?newdemand
?olddemand + 216 - ?oldsaleconsvalue\
calcNewOrder ?prod
?prodsel 216 ?newordervalue\
is ?neworder
?oldordervalue + ?newordervalue - ?oldsalevalue
Consequents:
and
demand2 ?cons
?newdemand\
order2 ?cons ?prod
?neworder
----------------------------------------------------------------------
Rule: TR-Demand-and-Order-2 (meta-accessible)
Antecedents:
and
demand2 ?cons
?olddemand\
sale2 ?prod ?cons
?oldsalevalue\
saleCons2 ?cons
?oldsaleconsvalue\
listSelProd3 [?prodsel
?other1 ?other2]\
order2 ?cons ?prod
?oldordervalue\
is ?newdemand
?olddemand + 233 - ?oldsaleconsvalue\
calcNewOrder ?prod
?prodsel 233 ?newordervalue\
is ?neworder
?oldordervalue + ?newordervalue - ?oldsalevalue
Consequents:
and
demand3 ?cons
?newdemand\
order3 ?cons ?prod
?neworder
----------------------------------------------------------------------
Rule: TR-Demand-and-Order-3 (meta-accessible)
Antecedents:
and
demand3 ?cons
?olddemand\
sale3 ?prod ?cons
?oldsalevalue\
saleCons3 ?cons
?oldsaleconsvalue\
listSelProd4 [?prodsel
?other1 ?other2]\
order3 ?cons ?prod
?oldordervalue\
is ?newdemand
?olddemand + 250 - ?oldsaleconsvalue\
calcNewOrder ?prod
?prodsel 250 ?newordervalue\
is ?neworder
?oldordervalue + ?newordervalue - ?oldsalevalue
Consequents:
and
demand4 ?cons
?newdemand\
order4 ?cons ?prod
?neworder
----------------------------------------------------------------------
Rule: TR-Demand-and-Order-4 (meta-accessible)
Antecedents:
and
demand4 ?cons
?olddemand\
sale4 ?prod ?cons
?oldsalevalue\
saleCons4 ?cons
?oldsaleconsvalue\
listSelProd5 [?prodsel
?other1 ?other2]\
order4 ?cons ?prod
?oldordervalue\
is ?newdemand
?olddemand + 266 - ?oldsaleconsvalue\
calcNewOrder ?prod
?prodsel 266 ?newordervalue\
is ?neworder
?oldordervalue + ?newordervalue - ?oldsalevalue
Consequents:
and
demand5 ?cons
?newdemand\
order5 ?cons ?prod
?neworder
----------------------------------------------------------------------
Rule: TR-Demand-and-Order-5 (meta-accessible)
Antecedents:
and
demand5 ?cons
?olddemand\
sale5 ?prod ?cons ?oldsalevalue\
saleCons5 ?cons
?oldsaleconsvalue\
listSelProd6 [?prodsel
?other1 ?other2]\
order5 ?cons ?prod
?oldordervalue\
is ?newdemand
?olddemand + 283 - ?oldsaleconsvalue\
calcNewOrder ?prod
?prodsel 283 ?newordervalue\
is ?neworder
?oldordervalue + ?newordervalue - ?oldsalevalue
Consequents:
and
demand6 ?cons
?newdemand\
order6 ?cons ?prod
?neworder
----------------------------------------------------------------------
Rule: TR-Price-1 (meta-accessible)
Antecedents:
and
saleProd1 ?prod ?mysales\
totalSales1
?totalSales\
price1 ?prod ?oldprice\
listChoiceProd2
?choices\
= ?choices [?sel1 ?sel2
?sel3]\
otherPrice ?otherprice
?choices price1 ?prod\
calcprice ?newprice
[?oldprice ?otherprice ?mysales ?totalSales]
Consequents:
price2 ?prod ?newprice
----------------------------------------------------------------------
Rule: TR-Price-2 (meta-accessible)
Antecedents:
and
saleProd2 ?prod
?mysales\
totalSales2
?totalSales\
price2 ?prod ?oldprice\
listChoiceProd3
?choices\
= ?choices [?sel1 ?sel2
?sel3]\
otherPrice ?otherprice
?choices price2 ?prod\
calcprice ?newprice
[?oldprice ?otherprice ?mysales ?totalSales]
Consequents:
price3 ?prod ?newprice
----------------------------------------------------------------------
Rule: TR-Price-3 (meta-accessible)
Antecedents:
and
saleProd3 ?prod
?mysales\
totalSales3
?totalSales\
price3 ?prod ?oldprice\
listChoiceProd4
?choices\
= ?choices [?sel1 ?sel2
?sel3]\
otherPrice ?otherprice
?choices price3 ?prod\
calcprice ?newprice
[?oldprice ?otherprice ?mysales ?totalSales]
Consequents:
price4 ?prod ?newprice
----------------------------------------------------------------------
Rule: TR-Price-4 (meta-accessible)
Antecedents:
and
saleProd4 ?prod
?mysales\
totalSales4
?totalSales\
price4 ?prod ?oldprice\
listChoiceProd5
?choices\
= ?choices [?sel1 ?sel2
?sel3]\
otherPrice ?otherprice
?choices price4 ?prod\
calcprice ?newprice
[?oldprice ?otherprice ?mysales ?totalSales]
Consequents:
price5 ?prod ?newprice
----------------------------------------------------------------------
Rule: TR-Price-5 (meta-accessible)
Antecedents:
and
saleProd5 ?prod
?mysales\
totalSales5
?totalSales\
price5 ?prod ?oldprice\
listChoiceProd6
?choices\
= ?choices [?sel1 ?sel2
?sel3]\
otherPrice ?otherprice
?choices price5 ?prod\
calcprice ?newprice
[?oldprice ?otherprice ?mysales ?totalSales]
Consequents:
price6 ?prod ?newprice
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-1 (meta-accessible)
Antecedents:
and
level1
'store-2'@simulation ?levelInValue\
saleProd1
'producer-2'@simulation ?salesProdInValue\
orderProd2
'producer-2'@simulation ?orderProdToday\
calcProductionDay
?orderProdToday 10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level2
'store-2'@simulation ?levelOutValue\
productionDay2
'factory-2'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-1 (meta-accessible)
Antecedents:
and
level1
'store-3'@simulation ?levelInValue\
saleProd1
'producer-1'@simulation ?salesProdInValue\
orderProd2
'producer-1'@simulation ?orderProdToday\
calcProductionDay ?orderProdToday
10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level2
'store-3'@simulation ?levelOutValue\
productionDay2
'factory-3'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-1 (meta-accessible)
Antecedents:
and
level1
'store-1'@simulation ?levelInValue\
saleProd1
'producer-3'@simulation ?salesProdInValue\
orderProd2
'producer-3'@simulation ?orderProdToday\
calcProductionDay
?orderProdToday 10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level2
'store-1'@simulation ?levelOutValue\
productionDay2
'factory-1'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-2 (meta-accessible)
Antecedents:
and
level2
'store-2'@simulation ?levelInValue\
saleProd2
'producer-2'@simulation ?salesProdInValue\
orderProd3
'producer-2'@simulation ?orderProdToday\
calcProductionDay
?orderProdToday 10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level3
'store-2'@simulation ?levelOutValue\
productionDay3
'factory-2'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-2 (meta-accessible)
Antecedents:
and
level2
'store-1'@simulation ?levelInValue\
saleProd2
'producer-3'@simulation ?salesProdInValue\
orderProd3
'producer-3'@simulation ?orderProdToday\
calcProductionDay
?orderProdToday 10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level3
'store-1'@simulation ?levelOutValue\
productionDay3
'factory-1'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-2 (meta-accessible)
Antecedents:
and
level2
'store-3'@simulation ?levelInValue\
saleProd2
'producer-1'@simulation ?salesProdInValue\
orderProd3
'producer-1'@simulation ?orderProdToday\
calcProductionDay
?orderProdToday 10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level3
'store-3'@simulation ?levelOutValue\
productionDay3
'factory-3'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-3 (meta-accessible)
Antecedents:
and
level3
'store-1'@simulation ?levelInValue\
saleProd3
'producer-3'@simulation ?salesProdInValue\
orderProd4
'producer-3'@simulation ?orderProdToday\
calcProductionDay
?orderProdToday 10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level4
'store-1'@simulation ?levelOutValue\
productionDay4
'factory-1'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-3 (meta-accessible)
Antecedents:
and
level3 'store-2'@simulation
?levelInValue\
saleProd3
'producer-2'@simulation ?salesProdInValue\
orderProd4
'producer-2'@simulation ?orderProdToday\
calcProductionDay
?orderProdToday 10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level4
'store-2'@simulation ?levelOutValue\
productionDay4
'factory-2'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-3 (meta-accessible)
Antecedents:
and
level3
'store-3'@simulation ?levelInValue\
saleProd3
'producer-1'@simulation ?salesProdInValue\
orderProd4
'producer-1'@simulation ?orderProdToday\
calcProductionDay
?orderProdToday 10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level4
'store-3'@simulation ?levelOutValue\
productionDay4
'factory-3'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-4 (meta-accessible)
Antecedents:
and
level4
'store-2'@simulation ?levelInValue\
saleProd4
'producer-2'@simulation ?salesProdInValue\
orderProd5
'producer-2'@simulation ?orderProdToday\
calcProductionDay
?orderProdToday 10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level5
'store-2'@simulation ?levelOutValue\
productionDay5
'factory-2'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-4 (meta-accessible)
Antecedents:
and
level4
'store-3'@simulation ?levelInValue\
saleProd4
'producer-1'@simulation ?salesProdInValue\
orderProd5
'producer-1'@simulation ?orderProdToday\
calcProductionDay
?orderProdToday 10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level5
'store-3'@simulation ?levelOutValue\
productionDay5
'factory-3'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-4 (meta-accessible)
Antecedents:
and
level4
'store-1'@simulation ?levelInValue\
saleProd4
'producer-3'@simulation ?salesProdInValue\
orderProd5
'producer-3'@simulation ?orderProdToday\
calcProductionDay
?orderProdToday 10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level5
'store-1'@simulation ?levelOutValue\
productionDay5
'factory-1'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-5 (meta-accessible)
Antecedents:
and
level5
'store-3'@simulation ?levelInValue\
saleProd5
'producer-1'@simulation ?salesProdInValue\
orderProd6
'producer-1'@simulation ?orderProdToday\
calcProductionDay ?orderProdToday
10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level6
'store-3'@simulation ?levelOutValue\
productionDay6
'factory-3'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-5 (meta-accessible)
Antecedents:
and
level5
'store-2'@simulation ?levelInValue\
saleProd5
'producer-2'@simulation ?salesProdInValue\
orderProd6
'producer-2'@simulation ?orderProdToday\
calcProductionDay
?orderProdToday 10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level6
'store-2'@simulation ?levelOutValue\
productionDay6
'factory-2'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-ProductionDay-and-Level-5 (meta-accessible)
Antecedents:
and
level5
'store-1'@simulation ?levelInValue\
saleProd5
'producer-3'@simulation ?salesProdInValue\
orderProd6
'producer-3'@simulation ?orderProdToday\
calcProductionDay
?orderProdToday 10 750 ?levelInValue 750 ?productionDayOutValue\
is ?levelOutValue
?levelInValue + ?productionDayOutValue - ?salesProdInValue
Consequents:
and
level6
'store-1'@simulation ?levelOutValue\
productionDay6
'factory-1'@simulation ?productionDayOutValue
----------------------------------------------------------------------
Rule: TR-Sales-1 (meta-accessible)
Antecedents:
and
level2
'store-3'@simulation ?levelStore\
order2
'consumer-2'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd2
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale2 'producer-1'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-1 (meta-accessible)
Antecedents:
and
level2
'store-1'@simulation ?levelStore\
order2 'consumer-2'@simulation
'producer-3'@simulation ?orderConsProd\
orderProd2
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale2 'producer-3'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-1 (meta-accessible)
Antecedents:
and
level2
'store-2'@simulation ?levelStore\
order2
'consumer-1'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd2
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale2 'producer-2'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-1 (meta-accessible)
Antecedents:
and
level2
'store-2'@simulation ?levelStore\
order2
'consumer-2'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd2
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale2 'producer-2'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-1 (meta-accessible)
Antecedents:
and
level2
'store-2'@simulation ?levelStore\
order2 'consumer-3'@simulation
'producer-2'@simulation ?orderConsProd\
orderProd2
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale2 'producer-2'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-1 (meta-accessible)
Antecedents:
and
level2
'store-3'@simulation ?levelStore\
order2
'consumer-3'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd2
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale2 'producer-1'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-1 (meta-accessible)
Antecedents:
and
level2
'store-1'@simulation ?levelStore\
order2
'consumer-3'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd2
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale2 'producer-3'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-1 (meta-accessible)
Antecedents:
and
level2
'store-3'@simulation ?levelStore\
order2
'consumer-1'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd2
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale2 'producer-1'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-1 (meta-accessible)
Antecedents:
and
level2
'store-1'@simulation ?levelStore\
order2
'consumer-1'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd2
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale2 'producer-3'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-2 (meta-accessible)
Antecedents:
and
level3
'store-1'@simulation ?levelStore\
order3
'consumer-1'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd3
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale3 'producer-3'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-2 (meta-accessible)
Antecedents:
and
level3
'store-1'@simulation ?levelStore\
order3
'consumer-2'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd3
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale3 'producer-3'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-2 (meta-accessible)
Antecedents:
and
level3
'store-3'@simulation ?levelStore\
order3
'consumer-3'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd3
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale3 'producer-1'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-2 (meta-accessible)
Antecedents:
and
level3
'store-3'@simulation ?levelStore\
order3
'consumer-2'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd3
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale3 'producer-1'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-2 (meta-accessible)
Antecedents:
and
level3
'store-1'@simulation ?levelStore\
order3
'consumer-3'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd3
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale3 'producer-3'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-2 (meta-accessible)
Antecedents:
and
level3
'store-2'@simulation ?levelStore\
order3
'consumer-1'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd3
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale3 'producer-2'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-2 (meta-accessible)
Antecedents:
and
level3
'store-2'@simulation ?levelStore\
order3
'consumer-2'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd3
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale3 'producer-2'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-2 (meta-accessible)
Antecedents:
and
level3
'store-2'@simulation ?levelStore\
order3
'consumer-3'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd3
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale3 'producer-2'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-2 (meta-accessible)
Antecedents:
and
level3
'store-3'@simulation ?levelStore\
order3
'consumer-1'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd3
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale3 'producer-1'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-3 (meta-accessible)
Antecedents:
and
level4
'store-3'@simulation ?levelStore\
order4
'consumer-2'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd4
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale4 'producer-1'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-3 (meta-accessible)
Antecedents:
and
level4
'store-1'@simulation ?levelStore\
order4
'consumer-1'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd4
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale4 'producer-3'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-3 (meta-accessible)
Antecedents:
and
level4
'store-1'@simulation ?levelStore\
order4
'consumer-2'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd4
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale4 'producer-3'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-3 (meta-accessible)
Antecedents:
and
level4
'store-1'@simulation ?levelStore\
order4
'consumer-3'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd4
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale4 'producer-3'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-3 (meta-accessible)
Antecedents:
and
level4
'store-2'@simulation ?levelStore\
order4
'consumer-1'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd4
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale4 'producer-2'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-3 (meta-accessible)
Antecedents:
and
level4
'store-3'@simulation ?levelStore\
order4
'consumer-3'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd4
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale4 'producer-1'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-3 (meta-accessible)
Antecedents:
and
level4
'store-2'@simulation ?levelStore\
order4
'consumer-2'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd4
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale4 'producer-2'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-3 (meta-accessible)
Antecedents:
and
level4
'store-2'@simulation ?levelStore\
order4
'consumer-3'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd4
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale4 'producer-2'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-3 (meta-accessible)
Antecedents:
and
level4
'store-3'@simulation ?levelStore\
order4
'consumer-1'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd4
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale4 'producer-1'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-4 (meta-accessible)
Antecedents:
and
level5
'store-3'@simulation ?levelStore\
order5
'consumer-3'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd5
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale5 'producer-1'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-4 (meta-accessible)
Antecedents:
and
level5
'store-1'@simulation ?levelStore\
order5
'consumer-1'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd5
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale5 'producer-3'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-4 (meta-accessible)
Antecedents:
and
level5
'store-2'@simulation ?levelStore\
order5
'consumer-3'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd5
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale5 'producer-2'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-4 (meta-accessible)
Antecedents:
and
level5
'store-3'@simulation ?levelStore\
order5
'consumer-2'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd5
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale5 'producer-1'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-4 (meta-accessible)
Antecedents:
and
level5
'store-2'@simulation ?levelStore\
order5
'consumer-2'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd5
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale5 'producer-2'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-4 (meta-accessible)
Antecedents:
and
level5
'store-2'@simulation ?levelStore\
order5
'consumer-1'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd5
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale5 'producer-2'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-4 (meta-accessible)
Antecedents:
and
level5
'store-1'@simulation ?levelStore\
order5
'consumer-3'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd5
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale5 'producer-3'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-4 (meta-accessible)
Antecedents:
and
level5
'store-3'@simulation ?levelStore\
order5
'consumer-1'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd5
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale5 'producer-1'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-4 (meta-accessible)
Antecedents:
and
level5
'store-1'@simulation ?levelStore\
order5
'consumer-2'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd5
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale5 'producer-3'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-5 (meta-accessible)
Antecedents:
and
level6
'store-1'@simulation ?levelStore\
order6
'consumer-2'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd6
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale6 'producer-3'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-5 (meta-accessible)
Antecedents:
and
level6
'store-1'@simulation ?levelStore\
order6
'consumer-3'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd6
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale6 'producer-3'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-5 (meta-accessible)
Antecedents:
and
level6
'store-3'@simulation ?levelStore\
order6
'consumer-3'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd6
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale6 'producer-1'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-5 (meta-accessible)
Antecedents:
and
level6
'store-3'@simulation ?levelStore\
order6
'consumer-2'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd6
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale6 'producer-1'@simulation 'consumer-2'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-5 (meta-accessible)
Antecedents:
and
level6
'store-2'@simulation ?levelStore\
order6
'consumer-3'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd6
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale6 'producer-2'@simulation 'consumer-3'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-5 (meta-accessible)
Antecedents:
and
level6
'store-2'@simulation ?levelStore\
order6
'consumer-1'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd6
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale6 'producer-2'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-5 (meta-accessible)
Antecedents:
and
level6
'store-1'@simulation ?levelStore\
order6
'consumer-1'@simulation 'producer-3'@simulation ?orderConsProd\
orderProd6
'producer-3'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale6 'producer-3'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-5 (meta-accessible)
Antecedents:
and
level6
'store-3'@simulation ?levelStore\
order6
'consumer-1'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd6
'producer-1'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale6 'producer-1'@simulation 'consumer-1'@simulation ?saleValue
----------------------------------------------------------------------
Rule: TR-Sales-5 (meta-accessible)
Antecedents:
and
level6
'store-2'@simulation ?levelStore\
order6
'consumer-2'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd6
'producer-2'@simulation ?orderProd\
calcSale ?levelStore
?orderProd ?orderConsProd ?saleValue
Consequents:
sale6 'producer-2'@simulation 'consumer-2'@simulation ?saleValue




(the number of rules
is smaller than the number reported in the previous appendix, as the model
suffered some improvements – in this version of the model some of the
transition rules do not write data for a final step )











There were eight ‘types’ of rules (see Table 12.1 involved in the application of the technique, those
associated with generating the dynamics of the simulation. Excluding those
rules for testing the theorem and setting up traders (producers)’ choices,
which did not suffer additional split, the other seven rules in the original
simulation model where split into 85 rules in the efficient simulation model.
All of them were split by transition step (TS) or iteration (five transitions);
among these seven rules, two suffered additional split by producer, and one,
among the last two, was also split by distributor (consumer). This gives: (5
+ (1 + (1 * 3)) * 3) * 5 = 85 rules in the new simulation model replacing
the referred seven rules in the old simulation model (this corresponds to the
last seven rules listed below and in Table
12.1). In the following the more relevant rules
will be presented. In the list, first the original rule is named and second the
names of the instances of the split rules as given in the module prover after
are given. More detail about these rules can be seen in the module prover given
in Appendix 1 section 10.2.3. Table
12.1 summarises facts about the performed splitting.
Checking
theorem –this rule was not split.
Rule: checkTheorem (meta-accessible)
Producers’
choice of a Producer for price-setting.
Rule: Choices-Iter-1
(meta-accessible)
Rule: Choices-Iter-2
(meta-accessible)
Rule: Choices-Iter-3
(meta-accessible)
Rule: Choices-Iter-4
(meta-accessible)
Rule: Choices-Iter-5 (meta-accessible)
Comment:
Split by
iteration. This rule had already been written specifically for each iteration
before splitting but without using a meta module. It was useful for
improving SDML’s efficiency when backtracking. In the MAS model all this rules
are fired previously to the transition rules, e.g., they fire outside the
partition of rules implementing the simulation transition steps.
Rule for
calculating distributors (or consumer)’ total order. It was split into:
Rule: Data-OrderProd-OrderCons-1
(meta-accessible)
Rule: Data-OrderProd-OrderCons-2
(meta-accessible)
Rule: Data-OrderProd-OrderCons-3
(meta-accessible)
Rule: Data-OrderProd-OrderCons-4
(meta-accessible)
Rule: Data-OrderProd-OrderCons-5 (meta-accessible)
Comment:
This rule was split only by
iteration.
Rule for
calculating traders (producers)’ total sales. Split into:
Rule: Data-SalesProd-OrderCons-1
(meta-accessible)
Rule: Data-SalesProd-OrderCons-2
(meta-accessible)
Rule: Data-SalesProd-OrderCons-3
(meta-accessible)
Rule: Data-SalesProd-OrderCons-4
(meta-accessible)
Rule: Data-SalesProd-OrderCons-5
(meta-accessible)
Rule for distributors
(consumers’) demand and order-setting. It was split into:
Rule: TR-Demand-and-Order-1
(meta-accessible)
Rule: TR-Demand-and-Order-2
(meta-accessible)
Rule: TR-Demand-and-Order-3
(meta-accessible)
Rule: TR-Demand-and-Order-4
(meta-accessible)
Rule: TR-Demand-and-Order-5 (meta-accessible)
Rule for
traders (producers)’ price-setting, it was split into:
Rule: TR-Price-1 (meta-accessible)
Rule: TR-Price-2 (meta-accessible)
Rule: TR-Price-3 (meta-accessible)
Rule: TR-Price-4 (meta-accessible)
Rule: TR-Price-5 (meta-accessible)
Rule for
traders (producer)’s sale-setting, it was split into:
Rule: TR-Sales-1 (meta-accessible)
Rule: TR-Sales-1 (meta-accessible)
Rule: TR-Sales-1 (meta-accessible)
Rule: TR-Sales-1 (meta-accessible)
Rule: TR-Sales-1 (meta-accessible)
Rule: TR-Sales-1 (meta-accessible)
Rule: TR-Sales-1 (meta-accessible)
Rule: TR-Sales-1 (meta-accessible)
Rule: TR-Sales-1 (meta-accessible)
Rule: TR-Sales-2 (meta-accessible)
Rule: TR-Sales-2 (meta-accessible)
Rule: TR-Sales-2 (meta-accessible)
Rule: TR-Sales-2 (meta-accessible)
Rule: TR-Sales-2 (meta-accessible)
Rule: TR-Sales-2 (meta-accessible)
Rule: TR-Sales-2 (meta-accessible)
Rule: TR-Sales-2 (meta-accessible)
Rule: TR-Sales-2 (meta-accessible)
Rule: TR-Sales-3 (meta-accessible)
Rule: TR-Sales-3 (meta-accessible)
Rule: TR-Sales-3 (meta-accessible)
Rule: TR-Sales-3 (meta-accessible)
Rule: TR-Sales-3 (meta-accessible)
Rule: TR-Sales-3 (meta-accessible)
Rule: TR-Sales-3 (meta-accessible)
Rule: TR-Sales-3 (meta-accessible)
Rule: TR-Sales-3 (meta-accessible)
Rule: TR-Sales-4 (meta-accessible)
Rule: TR-Sales-4 (meta-accessible)
Rule: TR-Sales-4 (meta-accessible)
Rule: TR-Sales-4 (meta-accessible)
Rule: TR-Sales-4 (meta-accessible)
Rule: TR-Sales-4 (meta-accessible)
Rule: TR-Sales-4 (meta-accessible)
Rule: TR-Sales-4 (meta-accessible)
Rule: TR-Sales-4 (meta-accessible)
Rule: TR-Sales-5 (meta-accessible)
Rule: TR-Sales-5 (meta-accessible)
Rule: TR-Sales-5 (meta-accessible)
Rule: TR-Sales-5 (meta-accessible)
Rule: TR-Sales-5 (meta-accessible)
Rule: TR-Sales-5 (meta-accessible)
Rule: TR-Sales-5 (meta-accessible)
Rule: TR-Sales-5 (meta-accessible)
Rule: TR-Sales-5 (meta-accessible)
Comment:
This rule was split not only by iteration
but also by producer and by consumer. When setting sales, a producer (trader)
can specify the data it is using by Producer (itself) and consumer (the one the
sale is intended to). That is why there appear nine rules for iteration (the
nine possible combination of three producers and three consumers). To make this
clearer, consider two rules of iteration 1 given below. The first rule involves
producer-2 and consumer-3, and the second rule involves producer-1 and consumer-3. Data involved in the precedent of these
rule are: level in store of the involved producer, order the involved consumer
has placed to the involved producer and total order placed to the involved
producer. In the consequent the two involved instance and the resulting value
of the sale are placed in a clause. Notice that the instances of producer,
consumer and store are instances pertaining to the simulation domain, as they
are generated during the simulation (this is indicated in SDML with the symbol @). As it is explained in Appendix 5, this specificity can be used
not only for achieving efficiency making rules dependencies more explicitly
instantiated but also for making assumptions and backtracking more specific,
and branch exploration more efficient.
Rule: TR-Sales-1 (meta-accessible)
Antecedents:
and
level2
'store-2'@simulation ?levelStore\
order2 'consumer-3'@simulation 'producer-2'@simulation ?orderConsProd\
orderProd2
'producer-2'@simulation ?orderProd\
calcSale
?levelStore ?orderProd ?orderConsProd ?saleValue
Consequents:
sale2 'producer-2'@simulation
'consumer-3'@simulation ?saleValue
------------------------------------------------------------------
Rule: TR-Sales-1 (meta-accessible)
Antecedents:
and
level2
'store-3'@simulation ?levelStore\
order2
'consumer-3'@simulation 'producer-1'@simulation ?orderConsProd\
orderProd2
'producer-1'@simulation ?orderProd\
calcSale
?levelStore ?orderProd ?orderConsProd ?saleValue
Consequents:
sale2 'producer-1'@simulation
'consumer-3'@simulation ?saleValue
Rule for
trader’s (producer)’ production and level updating. It was split into:
Rule: TR-ProductionDay-and-Level-1
(meta-accessible)
Rule: TR-ProductionDay-and-Level-1
(meta-accessible)
Rule: TR-ProductionDay-and-Level-1
(meta-accessible)
Rule: TR-ProductionDay-and-Level-2
(meta-accessible)
Rule: TR-ProductionDay-and-Level-2
(meta-accessible)
Rule: TR-ProductionDay-and-Level-2
(meta-accessible)
Rule: TR-ProductionDay-and-Level-3
(meta-accessible)
Rule: TR-ProductionDay-and-Level-3
(meta-accessible)
Rule: TR-ProductionDay-and-Level-3
(meta-accessible)
Rule: TR-ProductionDay-and-Level-4
(meta-accessible)
Rule: TR-ProductionDay-and-Level-4 (meta-accessible)
Rule: TR-ProductionDay-and-Level-4
(meta-accessible)
Rule: TR-ProductionDay-and-Level-5
(meta-accessible)
Rule: TR-ProductionDay-and-Level-5
(meta-accessible)
Rule: TR-ProductionDay-and-Level-5 (meta-accessible)
Comment:
This rule was split not only by iteration but also by
producer. This was possible because the updated producer (trader) variable only
depends on its own value last iteration and Producer can be instantiated
explicitly for each rule. In case there were some random choices or any other
manipulation involving generation of assumptions, this split would permit to
make them more specific and backtracking could be also implemented more
particularly.
Rule for ordering producer (trader) in order of value of
price
Rule: Data-SelProd-1
(meta-accessible)
Rule: Data-SelProd-2
(meta-accessible)
Rule: Data-SelProd-3
(meta-accessible)
Rule: Data-SelProd-4
(meta-accessible)
Rule: Data-SelProd-5 (meta-accessible)
Comment:
Data generated by this rule are
useful for consumers’ (distributors) order-setting and for calculating size of
the interval of prices when checking theorem.
|
Description of the rule (rule for:)
|
No. of rules in the original model
|
Rule split by
|
No. of rules in the efficient model
|
|
Checking theorem
|
1
|
---
|
1
|
|
Traders’ choice of a trader for price-setting
|
5
|
it had already been split by iteration
|
5
|
|
Rule for calculating distributors (or consumer)’
total order
|
1
|
iteration
|
5
|
|
Rule for calculating traders’ total sales
|
1
|
iteration
|
5
|
|
Rule for distributors (consumers’) demand and
order-setting
|
1
|
iteration
|
5
|
|
Rule for traders’ price-setting
|
1
|
iteration
|
5
|
|
Rule for trader’s sale-setting
|
1
|
iteration, trader and consumer
|
45
|
|
Rule for trader’s supply and level updating
|
1
|
iteration and trader
|
15
|
|
Rule for ordering trader in order of value of
price
|
1
|
iteration
|
5
|
|
Table 12.1. Comparing the number of
rules in the MAS-based and in the constraint-based architectures
|
|
Aspect
|
OTTER model
(Run in a SUN)
|
SDML model
after revealing dependencies (Run on a PC)
|
SDML Efficient
Model after unwrapping dependencies (Run on a PC)
|
|
Number of rules
implementing the transition step
|
13
|
13
|
91
|
|
Time the simulation
lasts using as unit of time the time required for one transition step in the
efficient model.
(see Appendix
5)
|
N (see note 4)4
|
N(N-1)/2
|
N
|
|
RAM Memory used
|
Typical: 3.328 MB1
|
256MB2
|
256 MB2
|
|
Hard Disk
Memory
used
|
- 0 in case the output file is
deleted.
- 100MB. Typical in case a
minimal amount of data is sent to the output file3.
|
0
But,
256 MB were needed if the SDML ‘image’ (file in RAM) was saved
|
0
But, 256 MB were needed if the image
was saved
|
|
Number of
backtrackings for proving over N iterations
|
8N
(N = 5 in the proof reported in
Chapter 7)
|
8N
|
8N
|
|
Dependencies
manager
|
User defined assumption tracking
mechanism
|
Automatic (It is a SDML’s facility)
|
Automatic (It is a SDML’s facility)
|
|
Underlying
logic of the language
|
Defined by the clauses of the sim.
model and hyperresolution
|
SDML underlying logic is close to
SGAL (Moss, et al., 1997)
|
SDML underlying logic is close to
SGAL (Moss, et al., 1997)
|
|
Table 13.1. Runs/Result Tables
|
Notes:
1:
Otter splits the search assigning, after a branch point, the search task of
each possible branch to a different process. In a typical moment during the
search there were five processes (each one responsible for a different split,
with each split corresponding to a transition step) each using the following
amount of RAM memory: 544 KB, 608 KB, 672 KB, 736 KB, 768 KB. Total: 3,328 KB
(or 3.328 MB).
2:
The total RAM memory available in the PC at that moment (December, 1999) was
256 MB.
3: It depends on
the required data to be sent to the output file. Default options controlling
sending of data to the output file, e.g., sending ‘given clauses’ or ‘kept
clauses’, can be cleared. In this case, after a proof, the file grew up to
about 100MB. Even in this case the output file can be too big. This file can be
deleted while the simulation is going on and then no hard disk memory will be
used.
4: Comparing in
terms of the manipulations but its speed is not comparable with the
implementations on SDML as it was run in a different platform.
The idea is to compare the
two architectures built in SDML after ‘revealing’ dependencies: the first one,
where only revealing of rule dependencies is implemented, and the efficient
one, where also ‘unwrapping’ of rules is used. The comparison will be in terms
of the amount of data each implementation searches into when generating a state
transition. This would give a rough idea about the speeding-up gained through the
technique, implemented in the second architecture and exposed in Chapter 7,
with respect to the MAS model.
Details about the
whole translation process from the original MAS model into the efficient
constraint-based architecture and, in particular, about revealing dependencies
and unwrapping of rules were given in Chapters 5 and 7 (see especially section 5.9.3). There, it can be seen how the space of searched
data grows after revealing dependencies and how this problem is managed in the
efficient implementation via unwrapping of rules.
In the efficient
program rules instantiate data more specifically. Discrimination among time
iterations speed up the simulation. Similarly, discrimination among agents and
objects can be exploited to add efficiency in the exploration of trajectories;
e.g., it can be used to drive the search more efficiently.
A ‘unit of data’ is
defined as the data generated in a single iteration (which does not change
significantly). As the efficient program searches into the data of one
iteration for each state transition (e.g., it uses data from iteration-i
to generate data for iteration-(i+1); see Chapters 5 and 7), it searches
into a unit of data for state transition. If a simulation trajectory were
generated per N iterations, then the size of the space of searched data
would be N-1 (there are N-1 time transitions).
On the other hand,
if the original implementation were used, the program would have to search into
one unit of data in the first transition (when the transition is from iteration-1
to iteration-2), two units in the second one, …, k-1 units at the
transition-k, and N-1 units at the final transition-(N-1).
So, in this case the amount of data searched in the whole simulation would be 1
+ 2 + .. + N-1 = N(N-1)/2 units. Finally, the factor of efficiency would be
the proportion between these two results: N/2. So, the efficiency of the
improved SDML-model is linearly increasing over time with respect to the
efficiency of the original SDML-model.
Likewise,
unwrapping of rules by agents and objects may be used for further improvements.
It would help to exploit the semantics of the simulation in order to add
efficiency during the search (though this was not implemented in the technique,
it is a strategy that will help in future applications). To explain this, it
should be remembered that assumptions are linked to a rule, i.e., assumptions
are generated when a rule is non-deterministic –as it can generate alternative
consequents. In this case, the rule causes a branch point where each possible
consequent has a different assumption and gives a different branch origin of a
different simulation trajectory. If were possible to instantiate data
explicitly (in fact, this is the case in the efficient implementation), then
data given in the original rule under the same assumption could now be
differentiated via assigning different assumptions, as they can be generated by
different rules. The idea is to make the branching as fine as possible in order
to make the backtracking also as specific as possible. To illustrate this,
consider the predicates used to give agents’ choices in Chapter 7:
Choice 1: listSelTrader(Trader-2,
Trader-1, Trader-1, i);
Choice 2: listSelTrader(Trader-2,
Trader-1, Trader-2, i);
Choice 3: listSelTrader(Trader-2,
Trader-3, Trader-1, i);
Choice 4: listSelTrader(Trader-2,
Trader-3, Trader-2, i);
Choice 5: listSelTrader(Trader-3,
Trader-1, Trader-1, i);
Choice 6: listSelTrader(Trader-3,
Trader-1, Trader-2, i);
Choice 7: listSelTrader(Trader-3,
Trader-3, Trader-1, i);
Choice 8: listSelTrader(Trader-3,
Trader-3, Trader-2, i);
For
each choice there will be a different assumption. In the implemented
simulations, when making a different choice, the computational system (SDML in
this case) assumes all traders’ choices change as they are linked to a single
assumption and so all data linked to the same assumption has also to be updated
when the assumption is changed. Should these choices be more specific, e.g., if
there were a different assumption for each trader’s choice, then there will
also exist a different branch for each trader’s choice. One choice can be
changed while keeping the others and only the data in the simulation linked to
that choice would be updated. Considering the choices listed above, assume choice
1 is left and choice 2 is taken, Trader-3’s choice (given by the third
component in the list) changes from Trader-1 to Trader-2 while
the other trader’s choices are kept unchanged.
In this case, where
only one trader changes his choice, e.g., assumptions and branching of the
simulation are more specific, backtracking might also be more specific as less
data has to be modified and regenerated for each backtracking. This would be
possible if, rather than writing a single rule for prices, this rule were split
and each trader’s choice could be given independently and linked to a different
assumption.
The aim of this appendix is to prove that the
exploration of trajectories proposed in Chapter 5 and explained more specifically
in section 5.5, applied over an infinite (theoretically) number of
iterations, is PSPACE-complete. To
make clearer the exposition, this problem will be called the target problem,
and the case where it appeared (that exposed in Chapter 7) the target
example. As is usual for this sort of proof, two steps will be
followed:
First, it will be proved that the target problem is in
PSPACE by expressing it as a binary tree of depth n. According to
Papadimitriou, this is sufficient (Papadimitriou, 1994; see examples in pp.
455-462).
Second, it will be proved that the problem is also PSPACE-complete
by translating another PSPACE-complete problem into the target problem.
For this comparison, one of the problems Woolridge
(2000) presents has been chosen, concretely that of agent-task-maintenance.
For the first part of the
proof it must be possible to construct in polynomial space the game three,
which is possible if the target problem is expressed in the form of a Boolean
quantified expression (see examples 19.1 and 19.2 in Papadimitriou, ibid), as follows:
∃x1
∀x2∃x3 ∀x4∃x5 … Qn xn (F) (1)
where F is the formula to be evaluated over
the variables x1
… xn, and Qn
is the last quantifier, which will be ∃ in case of n impair
and ∀ in case of n even.
The impair
variables correspond to the environment’s action. The deterministic part
in the state transition of the simulation will be called environment’s
actions. In the target example, it corresponds to all those changes not associated
with agents’ choices. Consequently, there is only one alternative action
for the impair variables. The even variables correspond to the
agents’ choices (which are going to be called agents’ actions). In the
target example, there are eight alternative agents’ choices. So far, a state
transition in a simulation has been divided into two parts: that deterministic
part associated with the existential variables and that non-deterministic
part associated with the quantified variables. A simulation path (a
trajectory) is represented by a concatenation of branches, where each branch
corresponds to an assignment of values to a variable xi.
Finally, F will be the question: whether the searched
tendency has occurred in a simulation trajectory, where that trajectory
is associated with an assignment of values for the variables, xi.
The whole expression (1) is true if for all possible assignments of values to
the variables the tendency is true (remember that there is only one choice for
the existential variables). As each particular assignment of values to the
whole set of quantified variables corresponds to a trajectory, the proof is
successful if this expression is valid for all possible values the quantified
variables can take? (e.g., for all possible agents’ choices).
|
|
|
Figure
15.1. Boolean circuit for the
target problem
|
To check if the proof is successful, a boolean circuit,
where and OR gate stands for the ∃ quantifier and an AND gate stands for the ∀ quantifier, will be written. A leaf in this
circuit is evaluated to true if the tendency is found in the
corresponding simulation path and to false otherwise (see Figure 15.1). The whole circuit will be true if and only
if the tendency appears in all simulation paths. Hence, the proof is successful
if and only if the circuit is true (e.g., the tendency is found in all
paths).
These two expressions of the problem are sufficient to prove
that the target problem is PSPACE. The next task is to prove that the problem
is PSPACE-complete.
Comparing with Woolridge (2000), an algorithm to check the
proof might be written. This will bring the example close to the one he uses
when considering maintenance tasks. Assuming a Turing machine M
is called recursively at each branch point (at agents’ choices) and that this
machine is kept in use while actions are deterministic (environment’s action),
the algorithm for M will be:
Algorithm 15.1:
1. If the tendency appears, then the branch is
evaluated to true (success);
2. If there are no allowable simulation
actions, the branch is evaluated to false (fail);
3. Execute the deterministic aspects of the
state transition (environment action), then for each agent’s choice recursively
call M;
4.
If all recursive
calls in 3, are successful (i.e., evaluated to true), then M
is true (success).
To prove that the target problem is PSPACE-complete,
consider the maintenance problem in Woolridge (2000). There, agents are chosen
non-deterministically to act against the environment. Each agent’s actions are
deterministic, while environment’s actions are non-deterministic. The idea is
to check if there is any choice of agents’ actions that is successful in
bringing the environment into one in a set of states whatever the environment
chooses. It is like a game where agents play against the environment. Woolridge
proves that the agent-maintenance problem is in NPSPACE using the following algorithm:
Algorithm 15.2:
1. if r [the run until a branch point] ends
with state Î G
[the set of goals], then M accepts;
2. if there are no allowable actions given r,
then M rejects;
3. non-deterministically choose an action α
from Ac (possible agents’ actions, there is one per agent) and then
for each e Î Г (set of possible environment’s states)
recursively call M with the run r. α. e;
4. if all of these accept, then M accepts,
otherwise M rejects.
In Woolridge’s problem, rather than searching for a
tendency, the idea is to bring the simulation into one among a set of
environment states. If the environment is brought into one of these states, it
is said that the selected agents have been successful in their game against the
environment. In Woolridge’s example, the agents’ actions are deterministic;
e.g., they have only one choice, but different agents can be selected.
Selection of agents corresponds to the OR nodes in the circuit shown in
the Figure 15.1, each branch corresponding to the choice of a
different agent. On the other hand, the environment has non-deterministic
actions, and, correspondingly, their choices are associated with the AND
gates in the circuit.
A first difference between algorithm 15.1 and
Woolridge’s algorithm (e.g., algorithm 15.2) is that in the latter the
recursive calls at step 3 are made for the environment choices, while in the
former they correspond to the called environment actions. A major difference is
that the deterministic action of the environment in step 3 in the former
algorithm corresponds to the non-deterministic choice of agents in the latter.
The translation of Woolridge’s problem into the target problem in this
presentation seems straightforward, but there is still a small difficulty: his
case study is non-deterministic (owing to the non-deterministic choice of
agents in step 3 in algorithm 15.2), while the target problem in this
presentation is deterministic.
Woolridge’s original problem is NPSPACE. Consider the deterministic
version of this problem. Think about checking the successfulness of agents’
actions in Woolridge’s problem once an agent has been chosen in advance at each
branch point. This is a deterministic problem. It is in PSPACE but still as
hard as Woolridge’s original one as NPSPACE = PSPACE (Papadimitriou, p.
150). These problems are both PSPACE-complete. Woolridge’s algorithm for
this deterministic version of the agent-maintenance tasks becomes:
Algorithm 15.3:
1. if r [the run until a branch point] ends
with state Î G
[the set of goals], then M accepts;
2. if there are no allowable actions given r,
then M rejects;
3. deterministically use the action α
given in advance from Ac (possible agents’ actions, there is one per
agent) and then, for each e Î Г (set
of possible sates of the environment), recursively call M with the run r.
α. e;
4.
if all of these
accept, then M accepts, otherwise M rejects.
The translation of the determinist version of Woolridge’s
problem into the target problem is straightforward from the algorithms 15.1
and 15.3. The deterministic action of the environment at step 3 of algorithm
15.1 corresponds in Woolridge’s algorithm (algorithm 15.3) to the deterministic action of the agent
already chosen. The recursive calls of M made for agents’ choices in algorithm
15.1 correspond in algorithm 15.3 to the environment’s choices. With
regard to the circuit shown in Figure
15.1, agents’ choices (now deterministic) are placed at
the OR gates and environment (non-deterministic) choices are placed at
the AND nodes. Therefore, the deterministic version of Woolridge’s
maintenance problem has been translated into the target problem, and,
consequently, the target problem is also PSPACE-complete.
It has been proved that the target problem is PSPACE-complete
for an infinite number of iterations, i. Using the experience
accumulated so far in this proof for i infinite (particularly useful is
the expression of the problem in the circuit given above), and theorems 17.8
(especially its corollary 2) and 17.10 in Papadimitriou (1994), it should be
possible to prove that the problem is ∑ i P-complete
if the number of iterations, i, is finite.
Presented at:
MABS2000
@ ICMAS-2000: The Second Workshop on Multi Agent Based Simulation, Boston, July
9, 2000.
Published in:
Moss, Scott and Paul Davidsson (eds.), Multi Agent Based
Simulation (MABS-2000), Lecture Notes in Artificial Intelligence, Vol. 1979,
Springer Verlag, Berlin
Presented at:
ATAL-2000: The Seventh International Workshop on Agent Theories, Architectures, and
Languages, Boston, July 7-9, 2000.
Published in:
Castelfranchi,
C. and Y. Lesperance (eds.), Intelligent
Agents VII, Agent Theories, Architectures, and Languages. Lecture Notes in
Artificial Intelligence, Springer-Verlag, Berlin
Abdennadher, S.
(1999), ‘Constraint Handling
Rules: Applications and Extensions’, Invited Talk, 2nd International
Workshop on Optimization and Simulation of Complex Industrial Systems.
Extensions and Applications of Constraint-Logic-programming and 7th
International Workshop on Deductive Databases and Logic-programming, Tokyo,
Japan, in conjunction with the 12th International Conference on Applications of
Prolog, INAP'99.
Abdennadher, S. and
H. Schütz (1997), ‘Model Generation
with Existentially Quantified Variables and Constraints’, Sixth
International Conference on Algebraic and Logic-programming, LNCS 1298,
Springer-Verlag, pp. 256-272.
Abdennadher, S., F.
Bry, N. Eisinger, and T. Geisler (1995), ‘The Theorem-prover Satchmo: Strategies, Heuristics, and Applications -
System Description’, Journées Francophones de Programmation en Logique,
JFPL'95, Dijon.
Ashby, William (1964), An Introduction to
Cybernetics, Methuen, London.
Axtell, R., R.
Axelrod, J. M. Epstein, and M. D. Cohen (1996), ‘Aligning Simulation
Models: A Case Study and Results’, Computational Mathematical Organization Theory,
1(2), pp. 123-141.
Barringer, H., M. Fisher, D. Gabbay, G. Gough, and A.
Hunter (1991), ‘Meta-Reasoning in Executable Temporal Logic’, in Proceedings
of the International Conference in Principles of Knowledge Representation and
Reasoning (KR), Cambridge, Massachusetts, April, Morgan Kaufmann.
Beavers, G. and H. Berghel (1992), ‘A Taxonomy of
Automated Theorem-proving Environments’, Proceedings of the 1992 Arkansas
Computer Conference, pp. 1-7 (accessible at http://www.acm.org/~hlb/publications/atp1/atp1.html).
Bohm, D., and D. Peat
(1989), Science, Order and Creativity, The
Guernsey Press, Channel Islands, UK.
Bry, François and
Adnan Yahya (1996), ‘Minimal Model
Generation with Positive Unit Hyperresolution Tableaux’, Lectures Notes in
Artificial Intelligence 1071, P. Miglioli, U. Moscato, D. Muncini and M.
Ornaghi (eds.), Proceedings 5th International Workshop TABLEAUX’96,
Terrasini, Palermo, Italy, May 1996, pp. 143-159.
Bonacina, Maria Paola (1998), ‘Theorem-proving
Strategies: A Search-Oriented Taxonomy’ (position paper), in Proceedings of
the Second International Workshop on First-order Theorem-proving (FTP),
Schloss Wilhelminenberg, Vienna, Austria, November 1998. Technical Report
E1852-GS-981, Technische Universität Wien, pp. 256-259.
Bonacina, Maria Paola (1999), ‘A Taxonomy of
Theorem-proving Strategies’, in Artificial Intelligence Today - Recent
Trends and Developments (invited paper), Lecture Notes in Artificial
Intelligence 1600, Springer,
Berlin, pp. 43-84.
Campbell, D. T. (1974), ‘Evolutionary Epistemology’,
in The Philosophy of Karl Popper, P.A. Schilpp (ed.), Open Court
Publish., La Salle, Ill., pp. 412-463.
Carley K., M.
Prietula, and Z. Lin (1998), ‘Design
Versus Cognition: The Interaction of Agent Cognition and Organizational Design
on Organizational Performance’, Journal of Artificial Societies and Social
Simuation 1(3) (accessible at: http://www.soc.surrey.ac.uk/JASSS/1/3/4.html).
Castelfranchi, C. and
Y. Lesperance (eds.) (2000), Intelligent
Agents VII. Agent Theories, Architectures, and Languages. --- 7th International
Workshop, ATAL-2000, Boston, MA, USA, July 7-9, Proceedings, Lecture
Notes in Artificial Intelligence, Springer-Verlag, Berlin.
Checkland, Peter and Jim Scholes (1999), Soft
Systems Methodology in Action: a 30-Year Retrospective, John Wiley,
Chichester, England.
Checkland, Peter (1981), Systems Thinking, Systems
Practice, John Wiley, Chichester, England.
Chiang, C. L. and R.C.T.
Lee (1973), Symbolic Logic and Mechanical Theorem-proving,
Academic Press, London, UK
Churchman, C. West
(1968), The Systems Approach,
Dell Publishing Co., New York.
Casti, John (1992), Reality Rules:II, Picturing the World in
Mathematics the – the Frontier, John Wiley
Publications, USA.
Conte, Rosaria,
Rainer Hegselmann, and Pietro Terna (1997), Simulating Social Phenomena, in Lecture Notes in Economics
and Mathematical Systems, Review Essay by Scott Moss in JASS 1(2), March,
1998, Springer-Verlag, Berlin (accessible at http://jasss.soc.surrey.ac.uk/1/2/review1.html)
Crowther Jonathan (ed.) (1995), Oxford Advanced
Learner’s Dictionary, 5th Edition, Oxford University
Press.
Crutchfield, James P. (1994a), ‘The Calculi of
Emergence: Computation, Dynamics, and Induction’, Physica D 75, pp.
11-54.
Crutchfield, James P. (1994b), ‘Observing Complexity
and The Complexity of Observation’, in Inside versus Outside, H.
Atmanspacher (ed.), Springer-Verlag, Berlin, pp. 234 - 272.
Crutchfield, James P. (1992), ‘Semantics and
Thermodynamics’, in Nonlinear Modelling and Forecasting, SFI Studies in
the Sciences of Complexity, Proc. Vol. XII, M. Casdagli and S. Eubank (eds.),
Addison-Wesley, Reading, Massachusetts, pp. 317-360.
Darley, V. (1994), ‘Emergent Phenomena and Complexity’,
in R. Brooks & P. Maes (eds.), Artificial Life IV, Proceedings of the
Fourth International Workshop on the Synthesis and Simulation of Living Systems,
The MIT Press, Cambridge, Mass, pp. 411-416.
DeLoach, Scott and
Mark Wood (2000), ‘Developing
Multiagent Systems with agentTool’, in Castelfranchi (2000).
Dewdey, A. K. (1993), The
(New) Turing Omnibus: 66 Excursions in Computer Science, Computer Science
Press, New York, USA.
Dix, J. (1994), Semantics of Logic Programs:
their Intuitions and Formal Properites. An Overview, University of
Koblenz-Landau, Germany.
Domingo Carlos and Giorgio Tonella (2000), ‘Towards a
Theory of Structural Change’, (invited paper for the 10th Anniversary issue of)
Structural Change and Ecomomic Dynamics, Scazzieri, R. (ed.),
10(3), pp. 1-18.
Domingo, C., T.
Jimenez, V. Ramirez, M. Sananes, O. Teran, and G. Tonella (1996a),
‘Simulation of Structural Change’, European Simulation Symposium, Genoa,
Italy.
Domingo
C., G. Tonella, and O. Terán (1996b), ‘Generating Scenarios by Structural
Simulation’, in AI, Simulation and Planning High Autonomy Systems, Univ.
of Arizona, pp 331-336.
Edmonds, Bruce (1995), ‘What is Complexity? - The
Philosophy of Complexity Per Se with Application to Some Examples in
Evolution’, in F. Heylighen & D. Aerts (eds.), The Evolution of
Complexity, Kluwer, Dordrecht, Netherlands.
Edmonds, Bruce (1998), ‘Meta-Genetic Programming:
Co-evolving the Operators of Variation’, CPM Report No.: 98-32 (accessible
at http://cfpm.org/cpmrep32.html).
Edmonds, Bruce (1999a), Syntactic Measures of
Complexity, doctoral thesis, Department of Philosophy, University of
Manchester, Manchester, UK.
Edmonds, Bruce (1999b), ‘Modelling Bounded
Rationality in Agent-Based Simulations using the Evolution of Mental Models’,
in Brenner, T. (ed.), Computational Techniques for Modelling Learning in
Economics, Kluwer, Dordrecht, Netherlands, pp. 305-332.
Edmonds, Bruce (1999c), ‘Gossip, Sexual Recombination
and the El Farol Bar: Modelling the Emergence of Heterogeneity’, Journal of
Artificial Societies and Social Simulation, 2(3) (accessible at http://www.soc.surrey.ac.uk/JASSS/2/3/2.html).
Edmonds, Bruce (1999d), ‘Capturing Social
Embeddedness: A Constructivist Approach’, Adaptive Behavior, 7, pp.
323-348.
Edmonds,
Bruce (2000),
‘Towards Implementing Free Will’, AISB'2000 Symposium on ‘How to Design a
Functioning Mind’, Birmingham, April 2000.
Edmonds, Bruce and S. Moss (1998), ‘Modelling
Economic Learning as Modelling’, Cybernetics and Systems, 29, pp. 5-37.
Edmund, Ronald, Moshie Sipper, and Matieu Capcarrere (1999),
‘Design, Observation, Surprise! A Test for Emergence’, Artificial Life
(5), pp. 225-239, Massachusetts Institute of Technology, Cambridge,
Massachusetts.
Engelfriet, J., C.
Jonker, and J. Treur (1998), ‘Compositional
Verification of Multi-Agent Systems in Temporal Multi-Epistemic Logic’, AI
Group, Vrije Universiteit Amsterdam, The Netherlands.
Fuenmayor, Ramses Leonardo (1986), The Ontology
and Epistemology of a Systems Approach : a Fundamental Study and an Application
to the Phenomenon Development/Underdevelopment, doctoral thesis, Lancaster University, Lancaster.
Fisher, Michael, Clare Dixon, and Martin Peim (2000),
‘Clausal Temporal Logic’, ACM Transactions on Computational Logic, vol
TBD, no. TBD, TBD TDB.
Fisher, Michael (1996), A Brief Introduction to
Concurrent METATEM, Logic and Computation Group, Department of Computing,
Spring, 1996 (accessible at: http://www.doc.mmu.ac.uk/STAFF/M.Fisher/cmet.html)
Fisher, M. and M. Wooldridge (1995), ‘A Logical
Approach to the Representation of Agents’, in N. Gilbert and R. Conte (eds.), Artificial
Societies, UCL Press, London.
Fitting, Melvin
(1990), First-Order Logic and
Automated Theorem-proving, Springer-Verlag, New York, USA.
Frühwirth, Thom (1994), ‘Constraint Handling Rules’, Constraint
Programming Basics and Trends, Lectures Notes in Computer Science 910,
Andreas Podelski (ed.), Springer-Verlag, Berlin, pp. 90-107.
Frühwirth, T., A. Herold, V. Küchenhoff, T. Le Provost,
P. Lim, E. Monfroy, and M. Wallace (1992), ‘Constraint Logic-programming
- An Informal Introduction’, in Logic-programming
in Action, G. Comyn et al.
(eds.), Springer, LNCS 636,
September.
Gell-Mann, Murray (1995), ‘What is Complexity’, Complexity,
1(1), pp. 16-19 (accessible at http://www.santafe.edu/sfi/People/mgm/complexity.html).
Gell-Mann, Murray (1995/96), ‘Nature Conformable to
Herself’, Complexity, 1(4) (accessible at http://www.santafe.edu/sfi/People/mgm/nature.html).
Gochet, Paul, Eric
Gregoire, Gribomont Pascal, Georges Louis, Edurardo Sanchez, Doninique Snyers,
and Pierre Wodon (1988), From
Standard Logic to Logic-programming, Thayse Andre (ed.), John Wiley &
Sons, Paris.
Grassberger, P.
(1989), ‘Problems in
Quantifying Self-Organized Complexity’, Helvetica Physica Acta, 62, pp.
489-511.
Heylighen, Francis
(1989), ‘Self-organisation,
Emergence and the Architecture of Complexity’, in Proceedings of the 1st
European Conference on System Science, AFCET, Paris, pp. 23-32.
Heylighen F. (1990), ‘Design of an Interactive Hypermedia
Interface Translating between Associative and Formal Problem Representations’, International
Journal of Man-Machine Studies, 35, pp. 491-5.
Heylighen, Francis
(1991a), ‘Cognitive Levels
of Evolution: from pre-rational to meta-rational’, in: The Cybernetics of
Complex Systems - Self-organization, Evolution and Social Change, F. Geyer
(ed.), (Intersystems, Salinas, California), pp.75-91.
Heylighen, Francis
(1991b), ‘Modelling
Emergence’, World Futures: the Journal of General Evolution (special
issue on Emergence), G. Kampis (ed.), pp. 89-104.
Heylighen, Francis
(1991c), ‘Coping with Complexity:
Concepts and Principles for a Support System’, Systemica, 8, part 1,
(special issue on Mutual Uses of Cybernetics and Science), R. Glanville
& G. de Zeeuw (ed.), pp. 39-55.
Heylighen, Francis
(1992), ‘Principles of Systems and
Cybernetics: an Evolutionary Perspective’, in Cybernetics and Systems
'92, R. Trappl (ed.), World Science, Singapore, pp. 3-10.
Heylighen, Francis
(1995), ‘(Meta)systems as
Constraints on Variation: a Classification and Natural History of Metasystem
Transitions’, World Futures: the Journal of General Evolution, 45, pp.
59-85, (accessible at: http://pespmc1.vub.ac.be/papers/PapersFH.html#RTFToC28).
Heylighen, Francis
(1997), ‘The Growth of Structural
and Functional Complexity during Evolution’, in The Evolution of Complexity,
F. Heylighen and D. Aerts (eds.), Kluwer Academic Publishers,
Dordrecht .
Heylighen, Francis
and Jan Bernheim (2000a), ‘Global
Progress I: Empirical Evidence for Ongoing Increase in Quality-of-Life’,
working paper of the CLEA study group ‘Evolution and Progress’ (accessible at http://pespmc1.vub.ac.be/papers/ProgressI&II.pdf).
Heylighen, Francis
and Jan Bernheim (2000b), ‘Global
Progress II: Evolutionary Mechanisms and their Side-effects’, working paper of
the CLEA study group ‘Evolution and Progress’ (accessible at http://pespmc1.vub.ac.be/papers/ProgressI&II.pdf).
Heylighen Francis
(2000c), ‘Foundations and
Methodology for an Evolutionary World View: a Review of the Principia
Cybernetica Project’, Foundations of Science, 5 (accessible at http://pespmc1.vub.ac.be/papers/PCPworldview-FOS.pdf).
Hoel, P. (1966), Introduction to Mathematical Statistics, John
Wiley, New York, USA.
Holland, J. (1998), Emergence: from Chaos to Order,
Addison-Wesley, Reading, Massachusetts.
Huberman, B. and T.
Hogg (1986), ‘Complexity and
Adaptation’, Physica 22D, North-Holland, Amsterdam, Netherlands.
Koen, V. Hindriks,
Frank S. de Boer, Wiebe van der Hoek, and John-Jules Ch. Meyer (2000), ‘Agent Programming with Declarative Goals’,
in Castelfranchi et al. (2000).
Konolige, K. (1995), ‘Autoepistemic Logic’, in Handbook of
Logic in Artificial Intelligence and Logic-programming / edited - Vol. 4:
Epistemic and temporal reasoning, Clarendon Press, Oxford, pp. 217-295.
Langton, C. (1989), ‘Artificial Life’, in C. G. Langton (ed.), Artificial
Life, vol. VI of SFI Studies in the Sciences of Complexity, Addison-Wesley,
Redwood City, CA, pp. 1-47.
Lifschitz, V. (1996), ‘Foundations of Logic-programming’,
in Principles of Knowledge Representation, CSLI Publications, pp. 69-127
(accessible at: http://www.cs.utexas.edu/users/vl/papers.html).
Liu, B., Jaffar J., and Yap R., (1999), ‘Constraint
Rule-Based Programming’, School of Computing, National University of Singapore,
Singapore (accessible at: http://www.comp.nus.edu.sg/~joxan/res.html).
Langton, C. G. (1989), ‘Artificial Life’, in Artificial Life,
volume VI of SFI Studies in the Sciences of Complexity, C. G.
Langton (ed.), Addison-Wesley, Redwood City, CA, pp. 1-47.
Loveland,
D. W. (1978), Automated
Theorem-proving: A Logical Basis, North-Holland Pub., Amsterdam.
Loveland, D.W. (1970), ‘A Linear Format for
Resolution’, Proc. IRIA Symp. Automatic Demonstration, Springer-Verlag,
New York, pp. 147-162.
Luckmand, D. (1970), ‘Refinements in Resolution
Theory’, Proc. IRIA Symp. Automatic Demonstration, Versailles, France,
1968, Springer-Verlag, New York, pp. 163-190.
Marriott, Kim and
Peter J. (1998), Programming
with Constraints: an Introduction, MIT Press, Cambridge, USA.
Maturana H. and F.
Varela (1980), Autopoiesis and
Cognition: the realization of the living, Reidel, Dordrecht.
McCune, W. (1995), OTTER 3.0 Reference Manual Guide,
Argonne National Laboratory, Argonne, IL.
Mihavics, K. and A. Ouksel (1996), ‘Learning to Align Organisational Design and
Data’, Computational Mathematical Organization Theory, 1(2), pp.
143-155.
Moss, S. (1998), ‘Social Simulation Models and
Reality: Three Approaches’, MAB’s 98: Multi-agent Systems and Agent-Based
Simulation, Paris (accessible at http://cfpm.org/cpmrep35.html).
Moss, S., H. Gaylard,
S. Wallis, B. Edmonds (1998a), ‘SDML: A Multi-Agent Language for
Organizational Modelling’, Computational Mathematical Organization Theory,
4(1), pp. 43-69.
Moss, S. and Claudia
Pahl-Worstl (1998b), Integrating
Physical and Social Modelling: The Example of Climate Change, CPM Report
no.: 98-47 (accessible at http://cfpm.org/cpmrep47.html).
Moss, S., B. Edmonds,
and S. Wallis (1997), Validation
and Verification of Computational Models with Multiple Cognitive Agents,
CPM-97-25 (accessible at http://cfpm.org/cpmrep25.html).
Nagel, Kai, Richard
J. Beckman, and Christopher L. Barrett (1998), ‘TRANSIMS for Transportation Planning’, short overview paper, to appear
in Proceedings of the International Conference on Complex Systems,
Nashua, NH (accessible at http://www.inf.ethz.ch/~nagel/papers/).
Nagel, Kai, Jorg
Esser, and Marcus Rickert (2000),
‘Large-scale Traffic Simulations for Transportation Planning’, long review
paper, Annual Review of Computational Physics, VII, Dietrich
Stauffer (ed.), World Scientific Publishing Company, Singapore.
Nicol, David and
Richard M. Fujimoto (1994),
‘Parallel Simulation Today’, Annals of Operations Research, (53), pp.
249—285.
Nigel G. and R. Conte
(eds.) (1995), Artificial Societies, University College London (UCL) Press,
London, UK.
Nigel, Gilbert (1995), ‘Emergence’, In Artificial
Societies, N. Gilbert and R.
Conte(eds.), UCL Press.
Papadimitriou, Christos (1994), Computational
Complexity, Addison-Wesley Publishing Company, California, USA.
Pritsker, A. Alan (1995), Introduction to
Simulation and SLAM II, John Wiley & Sons, New York, USA.
Rainer,
Manthey and Francois Bry (1988), ‘SATCHMO: A Theorem-prover Implemented in Prolog’, Lecture
Notes in Computer Science 910, ed. by G. Goos and J. Hartmanis, Springer-Verlag,
Proceedings 9th International Conference on Automated Deduction,
Argonne, Illinois, USA, May, pp. 415-434.
Reeves, Steve and
Michael Clarke (1990), Logic for
Computer Science, Addison-Wesley Publishing Company, Wokingham, UK.
Riley, Patrick, Peter
Stone, and Manuela Veloso (2000),
‘Layered Disclosure: Revealing Agents’ Internals’, in Castelfranchi et al. (2000).
Shapiro, Steven and
Yves Lesperance (2000), ‘Modeling
Multiagent Systems with CASL - A Feature Interaction Resolution Application’,
in Castelfranchi et al. (2000).
Simon, H. (1984), The Sciences of the Artificial, MIT
Press, Cambridge, Mass., USA.
Simon, H., E.
Massino, R. Marris, and R. Viale (1982), Economics, Bounded Rationality and the Cognitive Revolution, Edward
Elgar, Aldershot,.
Simon, Julian (1997), The Big Picture: Spectacular
Progress, Intellectual Capital.com (accessible at http://www.intellectualcapital.com/issues/97/1002/icbusiness.asp)
Solomon, Robert
(1996), Introducing
Philosophy: a Text with Integrated Readings, Harcourt Brace College
Publishers, Fort Worth, Tex, USA.
Stickel, M. (1990), ‘A Prolog Technology Theorem-prover:
A New Exposition and Implementation in Prolog’, International Symposium on
Design and Implementation of Symbolic Computation Systems, Capri, Italy.
Stickel,
M. Mark (1988), ‘A
Prolog Technology Theorem-prover’, Lecture Notes in Computer Science
910, eds. G. Goos and J. Hartmanis, Spring Verlag, Proceedings 9th
International Conference on Automated Deduction, Argonne, Illinois, USA,
May, pp. 752-753.
Stickel,
M. Mark (1986), ‘A
Prolog Technology Theorem-prover: Implemented by an Extended Prolog Compiler’,
Proceedings 8th CADE, J.
Automated Reasoning, Oxford, pp. 573-587.
Stone,
Peter and Manuela Veloso (1997), Multiagent Systems: A Survey from a Machine Learning
Perspective, School of Computer Science, Carnegie Mellon University,
Pittsburgh.
Stuart, R. and Peter
Norving (1995), Artificial Intelligence: a Modern Approach,
Prentice Hall International, Inc., Upper Saddle River, New Jersey, USA.
Terán, Oswaldo (1995), Simulación de Cambios Estructurales y Análisis
de Escenarios, master thesis, tutor C. Domingo, Instituto de Estadística
Aplicada y Computación, Universidad de los Andes, Venezuela.
Testa, Bernard and Lemont B. Kier (2000), ‘Emergence
and Dissolvence in the Self-organisation of Complex Systems’, Entropy
(accessible at www.mdpi.org/enropy/,
ISSN 1099-4300)
Turchin, Valenting (1977), The Phenomenon of
Science, Columbia University Press, New York.
Turchin, Valentin (1990), ‘Cybernetics and
Philosophy’, in Proc. 8th Int. Conf. of Cybernetics and Systems,
C.N. Manikopoulos (ed.), WOSC, New York (NOTE: Draft).
Turchin V. and C. Joslyn (1990), ‘The Cybernetic
Manifesto’, Kybernetes, 19, pp. 2-3.
Wack, P. (1985a), ‘Scenarios: Uncharted Waters Ahead’, Harvard Business Review, 63(5),
September-October, pp. 73-89.
Wack
P. (1985b),
‘Scenarios: Shooting the Rapids’, Harvard
Business Review, 3(6), November-December, pp. 139-150.
Weiss, Gerhard (ed.)
(1999), Multiagent Systems: a
Modern Approach to Distributed Artificial Intelligence, MIT Press,
Cambridge, Mass, USA.
Woolridge, Mike (2000), ‘The Computational Complexity of Agent Design
Problems’, in Proceedings Fourth International Conference on MultiAgent
Systems (ICMAS-2000), Boston, MA, USA, July 10-12, 2000, pp.
341-348.
Wos, L. (1984), Automated Reasoning: Introduction
and Applications, Prentice Hall, London.
Wos, L. (1988), Automated Reasoning: 33 Basis Research
Problems, Prentice Hall, London.
Wos, L., G. A.
Robinson., and Carson D. F. (1965),
‘Efficiency and Completeness of the Set of Support Strategy in
Theorem-proving’, J. ACM, 14, n° 4, pp. 698-709.
Zeigler, B (1990), Object-Oriented Simulation with Hierarchical,
Modular Model: Intelligent Agents and Endomorphic Systems, Academic Press,
Boston, Mass.
Zeigler, B. (1984), Multifaceted Modelling and Discrete Event
Simulation, Academic Press, London, UK.
Zeigler, B. (1976), Theory of Modelling and Simulation,
Robert E. Krieger Publishing Company, Malabar, Fl, USA.
![]() : a real vector of size n,
: a real vector of size n, ![]() : a real vector of size l,
: a real vector of size l, ![]() : a real vector of
size k,
: a real vector of
size k, ![]() : (state) at time t2 would be given by the
application of d
at time t1 (t2 > t1)
: (state) at time t2 would be given by the
application of d
at time t1 (t2 > t1) ![]() , l,
, l, ![]() >, where Y=
>, where Y=![]() and l are given as in the example, W is (
and l are given as in the example, W is (![]() , T), where T is defined as the positive
integers (e.g., 1, 2, …) and V=
, T), where T is defined as the positive
integers (e.g., 1, 2, …) and V=![]() , e.g., there are not
constraints.
, e.g., there are not
constraints.![]() (Y,T), where (w,r) Î R ®
(implies) dom((w) = dom (r )). The
relation between the input and output sets is distinguished, but it is not
possible to differentiate among the different outputs associated with one input
and vice versa.
(Y,T), where (w,r) Î R ®
(implies) dom((w) = dom (r )). The
relation between the input and output sets is distinguished, but it is not
possible to differentiate among the different outputs associated with one input
and vice versa. ![]() (Y,T) is a
function, and if f = (w,r) then dom (w) = dom (r )). At
this level, there is a function between input and output sets which permits one
to differentiate between the different outputs associated with an input. It is
granted by the knowledge of the initial
state. Until this level, a move from a lower level to a higher one allows
more predictability about the output, given the input, but still there is no
knowledge of the system’s states.
(Y,T) is a
function, and if f = (w,r) then dom (w) = dom (r )). At
this level, there is a function between input and output sets which permits one
to differentiate between the different outputs associated with an input. It is
granted by the knowledge of the initial
state. Until this level, a move from a lower level to a higher one allows
more predictability about the output, given the input, but still there is no
knowledge of the system’s states.![]() is equal to Q, then g and k are the
identity functions. The graph in Figure
2.2 becomes as shown in Figure
2.4, and equations 4 and 5 turn out to be:
is equal to Q, then g and k are the
identity functions. The graph in Figure
2.2 becomes as shown in Figure
2.4, and equations 4 and 5 turn out to be: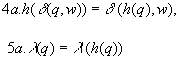
![]() ’ depends on the first component of
’ depends on the first component of ![]() , and the second component of
, and the second component of ![]() ’ depends on the remaining two and three components of
’ depends on the remaining two and three components of ![]() . As the relation among states is not one to one, this is not
an isomorphism (see Figure
2.5).
. As the relation among states is not one to one, this is not
an isomorphism (see Figure
2.5).![]()