ABSTRACT
Endowing agents with “social rationality” [10, 12, 11] can aid overall efficiency in tasks where cooperation is beneficial to system level performance. However it is difficult to maintain this beneficial effect in open and unpredictable systems. Such systems seem to require a “bespoke” design for cooperation in each domain. Recent work in artificial life and biological sciences has identified novel “tag” mechanisms for the spontaneous self-organization of group level adaptations in populations of autonomous agents [2, 3, 13, 16]. We summarize these findings and identify a key application (in MAS) to which these mechanisms may be fruitfully applied. An intriguing aspect of these mechanisms is that (in certain circumstances) there is a negative scaling cost – that is, the more agents in a system the better and more quickly organized they become. Also, since the process is driven by individual (bounded) optimization, agents retain a high degree of autonomy but still evolve behaviors that are socially rational even in open systems. Initial results indicate that the harnessing of such a process in MAS may be a viable alternative to the engineering of specific cooperation mechanisms and group structures.
Categories and Subject Descriptors
I.2.11 [Distributed
Artificial Intelligence]: Intelligent Agents, Multi-agent Systems.
General Terms
Algorithms, Performance, Design, Economics, Experimentation, Theory.
Keywords
Evolution of Groups, Tags, Social Cues, Cultural Markers, Altruism, Cooperation.
1. INTRODUCTION
Efficient scalable and robust multi-agent systems are difficult to engineer [8, 9]. One problem involves the design of individual agent decision-making processes that determine the appropriate actions for a given context or situation [15]. Designers often import ideas from classical economics and game theory (i.e. agents are engineered as rational individual utility optimizers [14]). However, “individual rational action” can produce inefficient, un-scalable and brittle outcomes at the level of the whole system [12]. Additionally, (as game theorists have made clear [1]) this kind of classical rationality suffers from two major defects: it is often too computationally expensive (or intractable); and, in many practical settings, it does not provide an effective guide to action choice because it may come up with a whole set of possible actions with no indication as to which action should be selected from a (possibly very large) set at a given point in time.
1.1 Social Rationality
One method of addressing this problem is to formulate a new kind of rationality for agents that takes into account the social costs and benefits of their individual action. This approach has been characterized as “socially responsible decision making” or “social rationality” [12]. Hogg and Jennings [6] succinctly define the concept thus:
Principle of
Social Rationality: If a socially rational
agent can perform an action whose joint benefit is greater than its joint loss,
then it may select that action.
However, although this kind of solution tackles the problem of system level efficiency, it does not address problems of scalability or robustness in practical settings. Neither does such an approach tackle problems of how agents will select from multiple equally beneficial socially responsible actions. More importantly in order to implement some level of socially rational behavior agents need to expend even more computational resources than for individual rationality – since a socially rational agent must take into account the collective (or social) costs and benefits of its own actions. It would therefore appear that a socially rational agent would require a sophisticated internal model of the MAS within which it is embedded. The presence of such an internal model will, almost certainly, greatly increase the computational cost for it is hard to see how increasing the size of a MAS would not produce a combinatorial explosion in time complexity for each agent’s decision making function. A further related issue is that unless agents were endowed with sophisticated induction processes that allowed them to build models of their social context (i.e. the MAS they are part of) then the implementation requirements of social rationality would have to change every time the composition or specific task domain of the MAS changed. This means that (given current techniques) agents cannot be endowed with a social rationality of a generic nature; rather for each specific MAS a bespoke implementation of the concept would be required.
Even assuming that the above difficulties could be overcome (and indeed just because something is hard does not rule it out of court) there is still the problem of robustness when an agent has to deal with other agents within a MAS that do not follow the same principle (e.g. due to either faulty internal models, imperfect information about the state of the MAS or pure maliciousness). Such a system could be incredibly brittle - malfunctioning or cheating agents could negate the potential benefits of social rationality.
Of course, Kalenka and Jennings [8] are cautions in their claims – they make it clear that social rationality will only bring benefits when it is ubiquitous within closed MAS and that such an assumption is appropriate if the aim is to engineering closed MAS. This may be true but is it really plausible? A substantial part of the appeal and potential power of the MAS paradigm comes from the potential for such systems to withstand open, noisy and unpredictable environments. Such environments mean that the MAS need to be scalable and adaptive and that there be some general approaches to producing such systems. We believe that new ideas emanating from evolutionary and adaptive simulations within the biological and social sciences [2, 3, 13, 16] are applicable here.
1.2 Evolving Social Rationality
We should make it clear that our aim is not to abandon the principle of social rationality stated above, but rather to find minimal adaptive mechanisms that bring it about in MAS – without the overheads and problems outlined in this introduction. Or put another way, we want social rationality to emerge from the interactions of autonomous agents, rather than have a designer design it for every situation. Moreover, we want to find generic methods that are applicable to many different task domains – such that agents can dynamically adjust their action selection functions. Finally we want such mechanisms to be robust, scalable and efficient.
In this paper we do not claim to have achieved these goals. But we do believe that we have identified an alternative approach that has real potential. This is achieved through the use of “tags” – observable social cues or markers attached to agents. These tags are visible (readable) by other agents allowing them to distinguish between agents with different tags[1]. Basically the approach is that one only aids other agents with sufficiently similar tags, and the system adjusts the degree of similarity required using an evolutionary mechanism.
1.3 Paper Overview
We proceed as follows. In sections 2 and 3 we describe a sequence of systems with increasingly complex and effective cooperation mechanisms. The empirical results from the later of these demonstrate characteristics very close to the requirements outlined. In these sections we also describe how the tag-mechanism works. We discuss how these findings can be applied within MAS. In section 4 we describe on-going work that puts the new approach to work in a realistic MAS task domain before concluding with a brief discussion.
2. A COMMON TRAGEDY
Our aim is to find minimal decision mechanisms that, when built into agents, produce socially rational solutions to common MAS coordination and cooperation problems. However, we wish to retain agent level autonomy and we want robustness and scalability. In order to address this problem we start with a very simple MAS coordination scenario in which classical individual rationality (individual utility maximization) produces poor system level performance. We will examine a commons dilemma [5] captured by the two-agent single round Prisoner’s Dilemma (PD) [1]. In the single round two-player PD each agent gets a choice from two possible actions (C or D). Depending on what actions they choose (and we assume they are autonomous in that neither agent can force the other to act in a given way or know in advance the move that will be made) an individual utility is awarded (see table 1).
Table 1. Utilities awarded to two
agents in single-round PD
|
|
|
Agent 2 action |
|
|
|
|
C |
D |
|
|
C |
R, R |
S, T |
|
D |
T, S |
P, P |
|
The dilemma is in the ranking of the utility payoffs: T>R>P>S and 2R>T+S. If agents exercise individual rationality (utility maximization) they will select action D and consequently both agents will be awarded P (the so called Nash Equilibrium). However, two agents acting in accordance with the principle of social rationality may both select actions C because this yields the highest joint benefit (since both get utility R and 2R is the highest joint outcome). Given this it would seem that to engineer an MAS in which the principle would hold would involve both agents recognizing the dilemma (by having a priori knowledge of the utility payoffs – a minimal internal social model) and then selecting the socially rational moves. If agents did not have such a priori knowledge or if other members of the MAS were not practicing the principle then the desirable 2R outcome could not be guaranteed.
But can agents learn to be socially rational without a priori knowledge of payoffs and other’s behaviors? Put another way, is there a simple learning mechanism that would allow agents to learn the socially rational solution in the single-round PD game? Below we describe two contrasting systems: M1 and M2, where M2 uses a tag-based decision mechanism. Whilst M1 results in individual rationality, M2 allows the emergence of a considerable amount of social rationality.
2.1 The M1 Model Gives Nash
Consider a very simple system model (we will call this model M1) composed of agents with very simple learning abilities. Each agent is represented by a single bit [0,1] and on-going interaction is represented by pairs of randomly selected agents playing a single round of PD. Agent bits are initialized at random. Agents possessing a “1” bit play C but agents possessing a “0” bit play D. Agents learn (change their behavior) by periodically mutating their bit with some low probability and copying the bit of other agents with higher utility than themselves.
If model M1 is executed in a simulation then we find that the Nash equilibrium of all D (all agents have a “0” bit) quickly predominates. This is intuitive since it those agents selecting action D will always do at least as well as their interaction partners. So model M1 (imitation of the more successful with some degree of autonomy – represented here by blind mutation) produces a Nash outcome that is not socially rational. What kind of simple learning model would produce a socially rational outcome? A simple yet novel mechanism using “tags” has been recently shown to solve this problem.
2.2 The M2 Model Gives Social Rationality
Consider another model (M2). This model is the same as M1 but each agent possesses some number L of additional bits that have no direct effect on the action selected by the agent. These bits are denoted as “tag bits”. The tag bits are observable by all agents. Figure 1 gives an outline of the simulation algorithm for model M2.
|
LOOP some number of generations LOOP for each agent (a) in the population Select a game partner agent (b) with the same tag (if possible) Agent (a) and (b) invoke their strategies and get appropriate payoff END LOOP Reproduce agents in proportion to their average payoff (with some, low, level
of mutation) END LOOP |
Figure 1. Outline algorithm for the simulation of model M2
Agents are selected to play a single-round of PD not randomly but based on having the same tag string. If an agent can find an individual with the same tag string as its own in the system it will play PD against that agent. If it cannot then it plays against some randomly chosen partner (as in M1). Agents learn in the same way as M1 but in addition mutate and copy tag bits in the same way as the action bit. If model M2 is implemented we find that if the number of tag bits is high enough (in this case we found 32 tag bits for a population of 100 agents to be sufficient) then the socially rational solution of all agents selecting action C predominates.
More interesting still, if all the agents are initially set to select action D then the time required to achieve a system where C actions predominate (consistent with the principle of social rationality) is inversely proportional to the size of the population. See figure 2[2]. This means that a larger sized MAS more quickly becomes socially rational. This is an inverse scaling phenomena: the more agents, the better! Additionally the fact that the system can recover from a state of total D actions to almost total C actions (under conditions of constant mutation) demonstrates the high robustness of the system. The socially rational solution is also the most efficient from the point of view of total utility attained by the system. The tag-based model M2 produces an efficient, scalable and robust solution – based on very simple individual learning methods.
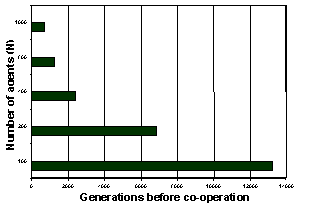
Figure 2. In model M2 the more agents in the system the quicker social rationality is attained
2.3 How Tags Work
We have presented the M2 model as a method for achieving three important properties in a simple (PD) task domain: efficiency, scalability and robustness. But how do tags produce this seemingly magical result? The key to understanding the tag process is to realize that agents with the same tag strings can be seen as forming a sort of “interaction group”. This means that the entire MAS can be considered as a collection of groups. If a group happens to be entirely composed of agents selecting action C (a socially rational group) then the agents within the group will outperform agents in a group composed entirely of agents selecting action D (an individually rational group). This means that more agents will copy the behavior of “socially rational” groups than “individually rational” groups. By copying the behavior and the tags of those who perform well, agents are essentially joining groups that are socially rational. However, if an agent happens to select action D within a group of action C agents then it will individually outperform any C acting agent in that (otherwise socially rational) group.
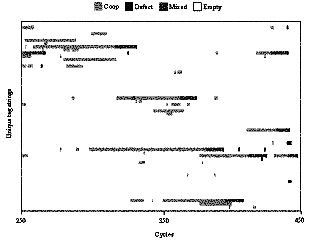
Figure 3. Notice that groups form, become invaded by agents performing D actions and then die
However, by others copying such an agent the group becomes very quickly dominated by D acting agents and therefore the relative advantage of the lone D acting agent is lost – the group snuffs itself out due to the interaction being kept within the group. So by selecting the D action an agent destroys its group very quickly (remember groups are agents all sharing the same tag string). Figure 3 visualizes this group process in a typical single run. Each line on the vertical axis represents a unique tag string. Groups composed of all C action agents are shown in light gray (Coop), mixed groups of C and D agents are dark gray and groups composed of all D are black.
The tag mechanism then, precipitates a kind of “group selection” process in which those groups which are more “socially rational” tend to predominate but still die out as they are invaded by mutant D acting agents. In a real sense the groups compete for resources despite the fact that evolution only occurs at the individual level and the agents don’t even know they are in such a group. In this system, the agents don’t die, just the particular groupings (based on sharing the same tag string) change. By constantly changing tag strings (by imitating those with higher utility) the agents produce a dynamic process that leads to high levels of C actions. In other words, the system as a whole contains a lot of cooperation occurring within a constantly changing system of groups, even though each agent is acting without any knowledge of the group structure and there is no central coordination of the groups[3]. Typically cooperative interactions in M2 reach over 90% of all interactions (over 100,000 cycles).
3. A COMPLEX TASK DOMAIN
Although model M2 manifests actions consistent with the principle of social rationality and produces efficient, robust and scalable properties, this is only with respect to a very simple scenario – namely the single-round PD. It could be argued that the tag processes are only applicable in such simple task domains. So we have developed a further model (M3) in which agents need to form groups with internal specialization and make altruistic donations of resources in order to reach a socially rational solution.
3.1 M3 Model – Altruism & Specialization
Here we describe a further model, M3. In this model, agents are selected at random and awarded resources. However, to “harvest” the resources agents require the correct skill. If they do not have the correct skill they may pass the resource to another agent with that skill (at a cost to themselves) or simply discard the resource. Figure 4 shows an outline algorithm for the simulation of M3. Each agent stores a single integer number representing its skill {1,2,3,4,5} (an agent can only store one skill). The agents use a slightly different tag representation (after Riolo et al [13]) than models M1 and M2. Each agent stores two real values: a tag from [0..1] and a tolerance (also in [0..1]). An agent considers another to be in its “group” if the absolute difference in their tag values is less-than-or-equal to the tolerance value of the agent. As in the previous models agents with higher utility (derived from harvested resources) are copied by others and mutation is applied with some small probability to skill, tag and tolerance values (minimally capturing innovation and autonomy). During a cycle of this model agents are selected at random and given some number of resources.
|
LOOP some number of generations (cycles) LOOP for each agent (a) in the population Award (a) some number of resources For each award to (a) if the resource can’t be harvested select an agent (b) with required tag and skill and donate (incurring a cost) END LOOP Reproduce agents in proportion to their utility (with some, low, level
of mutation) END LOOP |
Figure 4. Outline algorithm for the simulation of model M3
Each resource is associated with a skill (randomly selected). If the agent posses the correct skill then it will harvest the resource (and gain one unit of utility) but if the agent does not posses the required skill then it will search the population for an agent that is part of it’s group with the required skill and pass (donate) the resource (at a cost to itself). It would seem that agents with low tolerances (and hence small or empty groups) would perform well because they would not incur the costs of donation. However, the socially rational solution would be for groups to form with a diversity of skills.
3.2 Social Rationality Dependent on Awards
The individual rational action would be to discard all resources that could not be directly harvested, since passing them will incur a cost. Socially rational behavior would result in agents always donating resources (so long as the cost of passing the resource was lower than the credit received by the donating agent).
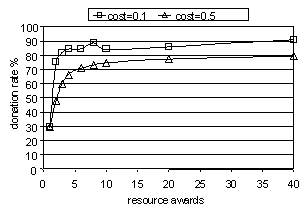
Figure 5. Donation rates against number of resources awarded to each agent in each cycle for model M3[4].
Figure 5 shows the results from execution of the simulation of M3. The number of resource awards is the number of times each agent is given a resource (in each cycle of the simulation) that it can keep, donate or discard. The donation rate is the proportion of times agents donate the resources they are awarded. The donation rate indicates the percentage of attempted donations (passes of resources) that result in success (i.e. find a recipient). Notice that the results show that neither pure individual rationality nor total social rationality dominates completely for all numbers of resource reward. However, note that for high donation rates to occur agents must form groups that contain a diversity of skills. Consequently we are asking a lot more from the simple learning process (compared to M2). Given this we still note that even when the cost of donation is half that of the benefit (cost = 0.5) to the receiving agent, there is still a donation rate of 30% for the lowest number of resources awarded per agent per cycle (this being 1 award). This is far from what individual rationality would produce (0%) but still means that 70% of resources are being wasted by the system – far from full social rationality. However when the number of resources awarded to each agent is increased this value quickly increases. When a resource award is set to 5 the donation rate is above 70% for both cost levels.
3.3 Summary of M3 results
Considering the simplicity of the learning system and the requirement that agents have to produce groups that are internally specialized this is a very promising result. However, we note that for M3 the level of efficiency is greatly effected by a model parameter (the number of awards). Additional experiments indicated that the system is scalable but does not posses the inverse scale property of M2 – essentially the same donation rates are obtained no matter what the size of the population is (so long as it is above about 50). The results given here were for populations of 100 agents. The system is robust to the constant mutation applied to agents[5] – indeed to produce the internal specialization of skills such “noise” is a requirement. Overall then our more complex task domain has eroded the level of social rationality manifested by agents but has still produced highly positive results given that no such decision process has been built-in to the agents and that there is the constant introduction of “cheating” (individually rational) agents (via mutation). Further experimentation with a similar model is given in Hales [4].
4. A REALISTIC TASK DOMAIN
The results from models M1, M2 and M3 have encouraged us to apply tag mechanisms to a more realistic MAS task domain. Here we detail on-going work with a model (M4) which is inspired by the MAS system detailed by Kalenka et al [12] which involves the control of warehouse robots servicing delivery trucks. We compare three action functions: an individually rational function, an engineered socially rational function and a self-organizing tag based function.
4.1 M4 Model – Robots in a Warehouse
Here we describe a further model M4 based on a task domain outlined by Kalenka et al [12]. Robots must work together to service the arrival of deliveries to a warehouse. There are ten loading bays into which trucks can arrive to be unloaded at any time (if the bay is empty). To each bay five robots are assigned to unload the trucks. While working, the robots unload at a constant rate. Robots are rewarded according to how much of the goods in their bay have been unloaded. Robots may help in the unloading of other bays but receive no reward for this. All the bays start empty. If a bay is empty, a truck of size s may arrive with a probability of p in each cycle. The truck stays there until it is empty, then it leaves. Thus the probability, p, is inversely related to the time the bay is empty and the truck size, s, related to the contiguous unloading time. Figure 6 gives an outline algorithm of the simulation of M4.
|
LOOP each cycle LOOP for each robot in last cycle Probabilistically choose a robot in proportion to fitness Mutate each of (tag, N, L) probability 0.1 End LOOP LOOP 5 times LOOP for each robot (A) IF lorry in own bay THEN ask robot (B) with same tag (or randomly choose if no tag match) IF (B) has lorry in its bay THEN (B) marked as a potential helper with A’s lorry if L is set ELSE (B) marked as potential helper for (A)’s lorry if N is set IF (A) marked as potential helper THEN randomly choose another who requested help. ELSE (A) unloads own lorry or sits idle End LOOP Each robot’s fitness = amount unloaded in own bay End LOOP |
Figure 6. Outline algorithm for the simulation of model M4
Each robot has a integer tag [1..500] which is visible to all the other agents. The tag-based mechanism is an evolutionary process that acts upon the tags of the robots as they do the unloading. In each cycle each agent can do a fixed number of units (5) of unloading. For each unit, if the agent has a lorry in its home bay it asks another agent for help. First it sees if there is another robot with an identical tag and asks them, if there is not it asks a randomly selected robot. Whether the asked robot responds with help depends upon its strategy, which is composed of two Boolean values: whether to help if it already has its own lorry to unload (L); and whether to help if it does not have a lorry to unload (N) – i.e. if it is idle. Thus the asked robot consults one of L or N depending on whether it has a lorry in its bay and acts accordingly.
At the beginning of each cycle the tag, N and L value triples are reproduced into the robot population probabilistically in proportion to the amount that the robot who had them had unloaded in its own bay. With a certain probability of mutation (0.1) these values are replaced with a random new value. Thus successful tags and response strategies are preferentially replicated to the robots for the new cycle. It is therefore likely that if a robot is relatively successful it will be replicated more than once and there will then be at least one other robot with the same tag to cooperate with. No contracts or joint / group utilities are used – the cooperation that emerges is entirely due to the implicit emergence of groups of robots with the same tags.
4.2 Comparing Three Decision Strategies
This simulation (tag) is compared to the two ‘hard-wired’ reference cases, where all robots are all: selfish or social. In the selfish case robots never help another robot and, hence, only unload trucks in their own bay. In the social case all robots unload from their own bay if there is a lorry there and always help another if there is not and it is requested to do so (i.e. robots will help others if idle and requested to do so). Each simulation was run for 500 cycles (which allows for each robot to unload a total of 2500 units). Statistics were collected about the simulation, including the percentage of time the robots were idle.
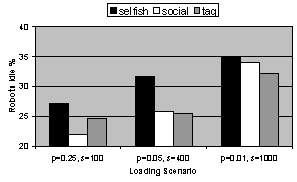
Figure 7. Total robot idle time for each loading scenario as a percentage of total robot time.
Figure 7 shows for each kind of decision function (or strategy) the total amount of time units wasted by robots sitting idle. An efficient system will minimize this value. Results are given for three different loading scenarios (different values of p and s). When p is small but s is large then deliveries are more sporadic, with lots of help required in bursts, but when p is high and s is low then jobs are arriving at a smother constant rate.
4.3 Tags Produce Efficient Solutions
The initial results for M4 shown in figure 7 demonstrate a very interesting property of the tag strategy. As expected the selfish strategy performs poorly since idle robots wont help others in other bays, the social strategy performs more efficiently than the tag strategy when p is high and s is low. However, for the two other loading scenarios the tag strategy outperforms the hardwired social strategy. It would seem that the system has self-organized to respond to the sporadic loading scenarios – we are currently investigating the exact dynamics that lead to this very encouraging result[6]. We speculate however, that the tag strategy allows agents to abandon unloading their own trucks in order to help with a newly arriving truck – which would potentially reduce idleness. This is something that the hardwired social agents cannot do. Here we believe we have found an example of the tag system producing a better solution than an intuitively hardwired socially rational solution.
5. DISCUSSION
In this paper we have presented a set of models that apply the same techniques to increasingly complex MAS task domain environments. There is much work within the areas of artificial life and societies and adaptive behavior that demonstrate (through simulation) potentially useful techniques for MAS. However, it is rare for such techniques to be applied in MAS. We believe that MAS can benefit from such techniques but that application to realistic domains requires significant translation and experimentation. We tentatively advance a process in which simple models are cumulatively brought closer to real application areas using simulation. We do not claim that the work presented here has fully achieved our aim but present it as an ongoing project which we believe has already demonstrated the possibility of our enterprise. Our ultimate aim would be to apply tag mechanisms to a real domain and produce improvements in efficiency, robustness and scalability over existing MAS engineering techniques.
However, we recognize the big difficulties in using simulation and large-scale adaptive systems to solve problems traditionally approached from a more orthodox engineering perspective. How can we prove that results from simulations will perform as we expect when applied to novel domains? How can we predict how such systems will behave in the future? We consider the kinds of systems presented here as “messy” [19] which are very similar to naturally occurring systems – such as real workers working in a warehouse. Do we have proofs for the human workforce? Does this stop human agents from achieving their goals in cooperative ways? See Edmonds [18] for a deeper discussion of the contrast between an a prior engineering approach (and its limitations) with a bottom-up simulation approach allowing social emergence.
All the models presented here are based on populations of agents making autonomous decisions based myopic and heuristic individual learning (imitation of other agents who have achieved higher utility over some period) there is no need for centralized decision making or bespoke design to restrict agent autonomy within the specific task domain. In each case the application of tags have moved the system away from individual rationality and towards socially rational collective solutions. Since the process concerned relies on noise (via mutation) the results are robust to the introduction of malicious or erroneous agents.
6. ACKNOWLEDGMENTS
We want to thank Scott Moss for creating the CPM (http://cfpm.org) and his commitment to the simulation approach. We wish to thank the creators of SDML [17] – an agent based simulation-programming language which model M4 was programmed in. The other models were constructed in JAVA2 by Sun (http://www.sun.com).
7. REFERENCES
[1] Binmore, K. Game Theory and the Social Contract Volume 1: Playing Fair. The MIT Press, 1994.
[2] Hales, D. Cooperation without Space or Memory – Tags, Groups and the Prisoner’s Dilemma. Multi-Agent-Based Simulation (eds. Moss, S., Davidsson, P.), Lecture Notes in Artificial Intelligence 1979. Berlin: Springer-Verlag, 2000.
[3] Hales, D. Tag Based Co-operation in Artificial Societies. Ph.D. Thesis, Department of Computer Science, University of Essex, UK, 2001.
[4] Hales, D. The Evolution of Specialization in Groups. Presented to the RASTA'02 workshop at the AAMAS 2002 Conference. To be published by Springer, (in press).
[5] Hardin, G. The tragedy of the commons. Science, 162:1243-1248, 1968.
[6] Hogg, L. M., and Jennings, N. R. Socially Rational Agents. Proc. AAAI Fall symposium on Socially Intelligent Agents, Boston, Mass., November 8-10, 61-63, 1997.
[7] Holland, J. The Effect of Labels (Tags) on Social Interactions. SFI Working Paper 93-10-064. Santa Fe Institute, Santa Fe, NM. 1993.
[8] Jennings, N. R. Agent-based Computing: Promise and Perils. Proc. 16th Int. Joint Conf. on Artificial Intelligence (IJCAI-99), Stockholm, Sweden. (Computers and Thought award invited paper) 1429-1436. 1999.
[9] Jennings, N. R. On Agent-Based Software Engineering. Artificial Intelligence, 117 (2) 277-296, 2000.
[10] Jennings, N., and Campos, J. Towards a Social Level Characterization of Socially Responsible Agents. IEE Proceedings on Software Engineering. 144(1):11-25, 1997.
[11] Kalenka, S. Modelling Social Interaction Attitudes in Multi-Agent Systems. Ph.D Thesis. Department of Electronics and Computer Science, Southampton University, 2001.
[12] Kalenka, S., and Jennings, N.R. Socially Responsible Decision Making by Autonomous Agents. Cognition, Agency and Rationality (eds. Korta, K., Sosa, E., Arrazola, X.) Kluwer 135-149, 1999.
[13] Riolo, R., Cohen, M. D. and Axelrod, R. Cooperation without Reciprocity. Nature 414, 441-443, 2001.
[14] Russell, S. and Wefald, E. Do The Right Thing: Studies in Rationality. MIT Press, 1991.
[15] Russell, S. Rationality and Intelligence. Artificial Intelligence, 94(1):55-57, 1997.
[16] Sigmund & Nowak. Tides of tolerance. Nature 414, 403-405, 2001.
[17] Moss, S., Gaylard, H., Wallis, S. and Edmonds, B. SDML: A Multi-Agent Language for Organizational Modelling. Computational and Mathematical Organization Theory, 4, 43-69. 1998
[18] Edmonds, B. Social Embeddedness and Agent Development. UKMAS'98, Manchester, December 1998, (http://cfpm.org/cpmrep46.html), 1998
[19] Moss, S. Policy analysis from first principles. Proceedings of the U.S. National Academies of Science, Vol. 99, Supp. 3, pp. 7267-7274, 2002.