Group Reputation Supports Beneficent Norms – A case of “them” and “us”
CPM Working Paper 02-101 (July 2002)
David Hales
Centre for Policy Modelling, The Business School
Manchester Metropolitan University, Manchester, UK.
E-mail: dave@davidhales.com
Web: www.davidhales.com
Abstract
This paper demonstrates the role of group normative reputation in the promotion of an aggression reducing possession norm in an artificial society. A previous model of normative reputation is extended such that agents are given the cognitive capacity to categorise other agents as members of a group. In the previous model reputational information was communicated between agents concerning individuals. In the model presented here reputations are projected onto whole groups of agents (a form of “stereotyping”). By stereotyping, norm followers outperform cheaters (who do not follow the norm) under certain conditions. Stereotyping, by increasing the domain of applicability of a piece of reputational information, allows agents to make informed decisions concerning interactions with agents which no other agent has previously met. However, if conditions are not conducive, stereotyping can completely negate norm following behaviour. Group reputation can be a powerful mechanism, therefore, for the promotion of beneficent norms under the right conditions.
1. Introduction
The computational study of norms through artificial society simulation stretches back a good ten years (Shoham and Tanneholtz 1992, Conte and Castelfranchi 1995, Walker and Wooldridge 1995, Castelfranchi, Conte and Paolucci 1998, Saam and Harrer 1999, Staller and Petta 2001, Flentge, Polani and Uthmann 2001,Conte and Paolucci 2002).
It is important to note that no unified or generally accepted definition of a social norm exists and this is productively evidenced by the differences in the models presented and conclusions drawn in previous computational work on norms[1]. However, in general, much of the work has tended to focus on prescriptive beliefs concerning proper behaviours within given social contexts. More specifically, interest is often focused on the kinds of norms that appear to contradict the narrow view of individual self-interest typified by classical rational actor theories[2]. The focus of this paper is also on these kinds of norms.
The resolution of social situations in which individual agent interests (or goals) conflict with group or system-level interests (or goals) are obviously a cornerstone of many theories of society (Hobbs 1962), but interestingly, are increasingly becoming issues within the agent engineering community (Jennings and Campos 1997, Kalenka and Jennings 1999). The vision of self-organising, open and productive multi-agent software systems appears to demand new kinds of rigorous “computational social theory”. In the absence of any adequate analytical tools for dealing with complex adaptive systems, at the level of detail required, simulation and empirical analysis appears to offer the best way forward.
The aim of this paper is not to provide a complete or general solution to the problem of why self-interested agents might follow and / or enforce socially beneficial norms[3]. Rather it is to introduce the concept of group reputation and indicate how this kind of social cognition combined with communication can support socially beneficent norms within given contexts.
What can artificial societies bring to the discussion about norms? Two issues can be addressed; firstly, by precise specification and experimentation (incrementally adding agent abilities) an understanding can be gained of the impact of individual processes. Secondly, by realising the processes computationally, findings can potentially be applied (at least as an initial guide) within the computational agent engineering community – which is becoming increasingly concerned with how to control large, possibly open systems of software agents (Moss 2002).
The computational model presented here is an extension of a framework first introduced by Conte and Castelfranchi (1995)[4]. We present this basic framework (section 2) and then give replication results from a slightly changed re-implementation of the model[5]. We then replicate studies with an extended model (Castelfranchi, Conte and Paolucci 1998) that includes reputation and communication of reputation (section 4). The model is further extended (section 5) to include group reputation and a set of new results is presented. Finally, conclusions and future directions of investigation are given (section 6).
The main findings presented are that group level normative reputation can reduce the costs incurred by followers of a socially beneficial norm such that the norm followers outperform those who do not follow the norm (the cheaters). But this only occurs under the condition that the population is partitioned into strategy homogenous groups – i.e. when the groups fit a “stereotype” perfectly (the members of a group are either all norm followers or all cheaters). In this context stereotyping works because the generalisation (to group level reputation) is true. However, when this condition does not hold the norm following behaviour is obliterated due to bad reputations being amplified by negative interactions produced by the stereotyping.
Readers wishing to apply the results given here to human social processes should exercise caution. This work presents experiments within an artificial society – and no attempt has been made to validate the assumptions of the model with respect to any actual target. Well-specified mechanisms are presented which produce given outcomes. The use-value of this kind of work is that findings may be interpreted as potential guiding criteria for hypotheses applicable to human societies and possible techniques for computationally engineered societies[6] where the function of reputational mechanisms is becoming increasingly relevant – see Conte and Paolucci (2002). With these qualifications in mind some possible insights are discussed later (section 6).
2. The Model
The model follows (Conte and Castelfranchi 1995) as a minimal way of capturing the notions of a possession norm and its effect on reducing aggression between agents. Also the model is extended in line with (Castelfranchi, Conte and Paolucci 1998) to include agents with social knowledge (reputation) and the ability to communicate that knowledge (gossip). The model was not re-implemented in exactly the same way – a number of assumptions were relaxed (discussed later). These assumptions were not identified by the previous work as significant, so the initial attempt to replicate results was a test of the robustness of the previous conclusions drawn. The results are also comparable to previous replication in which the assumptions were relaxed in a slightly different way (Nicole and Harrer 1999).
The Basic Model
The environment comprises a two-dimensional 10 x 10 grid with edges wrapped to form a torus. At any time, each cell in the grid can either be empty, occupied by a single agent, occupied by a single food item or occupied by an agent and a single food item (these are the only possibilities).
The environment is populated (initially) with 50 agents. Each agent has an energy level. If an agents’ energy level falls to zero it dies and is removed from the environment. Agents have the goal of finding and consuming food items in order to increase their energy levels. Each action an agent performs has an associated energy cost. Consequently agents need to consume food items to stay alive. Depending on the context an agent may select from several possible actions: movement of one cell within the von Neumann neighbourhood (VNN), to eat food in the current cell, to attack an agent in an adjacent cell holding food or to simply do nothing.
Agents have two forms of perception. They can “see” food items and other agents one cell away (within the VNN) and can “smell” food items two cells distant (within the VNN). Figure 1 illustrates the reach (shaded areas) of each of these regions on the grid.
If an agent senses a food item nearby (using its senses of “sight” and “smell”) it moves one cell toward it. If an agent finds itself within the same cell as a food item it attempts to consume (“eat”) it. Eating involves the agent staying in the same cell with the food item for two actions[7]. These actions have been characterised as (“pickup food” and “prepare food” – see table 1 below). After these two actions have been performed the agent can eat the food. Immediately after eating the energy from the food item is added to the agents’ energy level and the food item is removed from the environment. A new food item is created and placed in a random cell (which does not already contain food) in the environment. This renewal of resources keeps the number of food items in the environment constant at all times.
In all the experiments reported here the number of food items is set at 25, each having energy value 20. Initially food items are distributed uniformly randomly over the grid of cells (but with a maximum of a single food item in any single cell).
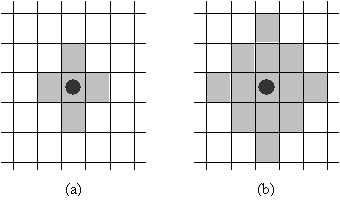
Figure 1. Agents (shown as a black circle) can see and move within one cell of the von Neumann neighbourhood (VNN) – see (a). However, they can smell for food within two cells of the VNN – see (b).
If an agent can not see an adjacent free food item or smell a more distant one then it will consider any possible attacks it may make on other agents that possess food. If an adjacent cell (VNN) containing an agent eating a food item is seen then an agent may decide to attack and take possession of the food item. When deciding to attack the agent refers to an attack “strategy”. Each agent is allocated a strategy from one of three: 1) Blind: always attack; 2) Strategic: attack if the enemy is not stronger (higher energy level); 3) Normative: a “possession norm” is observed. Attack only if the enemy does not own the food item and is not stronger. Food items are flagged as “owned” by the nearest agent, spatially, when the food item is created. When an agent attacks another adjacent (eating) agent, 4 energy units are deducted from both agents. The food item is then moved to the attacker if it has a higher strength (energy level) – i.e. the attacker “steals” the food. If the attacker is successful in snatching the food item, it must then (as stated previously) go through the actions of “pick-up” and “prepare” before it can “eat” the item.[8]
If an agent can make no attacks then it makes a random move. If it can not make a random move (say it was surrounded by 4 other adjacent agents) then it “pauses” – i.e. does nothing. Each action an agent can perform has a cost that is subtracted from the energy level of the agent. For the experiments reported here cost are as follows: move = 1; attack = 4; being attacked = 4; all other actions cost nothing (0). If an agents’ energy level falls to zero or below then the agent immediately “dies” and is removed from the environment[9] (see table 1 for a summary of the possible agent actions and their energy costs).
In all the experiments presented in this paper the 10 x 10 torus grid was initially filled with 50 agents and 25 food items[10]. The initial energy level for each agent is 40. Food items are worth 20. For each experiment 100 runs with different pseudo-random number seeds were executed. A run consisted of 2000 cycles (a “cycle” is defined below).
|
Table 1: Possible Agent Actions and Associated Energy Costs |
||
|
Agent Action |
Energy |
Description |
|
Move |
-1 |
Move one square in the VNN. |
|
Pickup Food |
0 |
Pick-up food in current cell |
|
Prepare Food |
0 |
Prepare food currently held |
|
Eat Food |
+20 |
Eat prepared food |
|
Attack |
-4 |
Attack an adjacent agent with food |
|
Pause |
0 |
Do nothing |
Previous papers that introduced and developed this model (Conte et al 1995, Castelfranchi et al 1998) specified that agent actions were simultaneous and synchronous. In later work (Saam and Harrer 1999) the assumption of simultaneous action was relaxed such that agents acted in sequence. In this new re-implementation agents are selected from the population randomly (with replacement) and allowed to take an action. A “cycle” is considered to have occurred after 50 (the population size) agents have been selected[11] (see figure 1 for a pseudo-code overview of a single cycle). Essentially this relaxation of synchronous interaction produced results that are qualitatively comparable to Conte et al (1995) and Castelfranchi et al (1998) and quantitatively more in line with Saam and Harrer (1999) – as would be expected.
Reputation and Communication
In Castelfranchi et al (1998) the model so far described was extended to incorporate social knowledge (agent reputation) and communication of that knowledge. Each normative agent stores a flag for each agent in the population. If a normative agent is attacked by another agent while eating food it owns then the attacking agent is flagged by the attacked agent as a “cheater” (an agent that does not follow the possession norm). In subsequent encounters agents flagged as cheaters will have the strategic attack strategy applied. In this mode, reputations (the flags) are stored in each normative agent and are updated only via the direct experience of each individual agent – no communication occurs. Experiments were conducted with mixed populations where half of the population employed this form of individual reputation.
Communication of reputation was also implemented in the previous extensions such that those norm following agents not flagged as cheaters (so called “respectful agents”) pool their knowledge when they meet as neighbours on the grid. This is implemented by allowing each norm following agent selected for an action to first add knowledge from neighbours (in the VNN) that it believes to be respectable (i.e. are not flagged already as cheaters). This form of information pooling is monotonic - agents flagged as cheaters can never have the flag reversed[12].
|
One Cycle: LOOP
50 times Select an agent (A) at random
from the population (with replacement) Activate agent – (agent (A)
selects and executes one action): IF appropriate
– receive reputational information from all neighbours IF current
cell contains food then IF
food prepared then {EAT-FOOD} IF
food picked-up then {PREPARE-FOOD} IF
food not-picked-up then {PICKUP-FOOD} END IF IF free food
item is visible in neighbourhood {MOVE} to food item. IF a food item
can be smelled two cells away then {MOVE} towards it. IF an agent
holds a food item one cell away in neighbourhood then IF
current strategy allows then {ATTACK} END IF IF any
neighbouring cells are free then select one at random and {MOVE} No other
actions are possible so {PAUSE} END
LOOP |
Figure 1. A pseudo-code outline algorithm of what happens in a single cycle. Note that the actions (in curly brackets {}) indicate the selected actions by the agent. Implied in the algorithm is that each action is followed immediately by and “exit” which shifts control to the END LOOP line (ready for the next iteration). In all case where several options exist (i.e. were the agent can see several free food items or several agents to attack) a random choice is made.
3. Basic Model Replication Results
As with the previously published results (Conte et al 1995) statistics were gathered over 100 individual runs (with different pseudo-random number seeds) for each experimental scenario. Each single run comprised 2000 cycles, a cycle being 50 agent action steps, as outlined previously in figure 1. For implementation details and links to code see appendix 1.
Measures of total strength (energy of all agents added together at the end of the run), the inequality of strength (standard deviation of energy levels over the population) and the total number of aggression acts (cumulative number of attacks made over the entire run) were collected for 100 runs and averaged. Also, standard deviations were calculated over the 100 runs to give an indication of spread.
3.1 Strategy Homogenous Experiments
Table 2 and Figure 3 show both the previous results (a) and the replication results (b) for strategy homogenous populations (i.e. when all agents follow the same strategy).
|
Table 2: Homogenous population results |
||||||
|
Results from
Conte et al (1995) |
||||||
|
Strategy |
Str |
st.dev |
Var |
st.dev |
Agg |
st.dev |
|
Blind |
4287 |
204 |
1443 |
58 |
9235 |
661 |
|
Strategic |
4727 |
135 |
1775 |
59 |
4634 |
248 |
|
Normative |
5585 |
27 |
604 |
41 |
3018 |
76 |
b) Replication results |
||||||
|
Strategy |
Str |
st.dev |
Var |
st.dev |
Agg |
st.dev |
|
Blind |
3863 |
121 |
1652 |
52 |
15943 |
874 |
|
Strategic |
4134 |
110 |
1880 |
50 |
5120 |
239 |
|
Normative |
4451 |
26 |
479 |
30 |
940 |
32 |
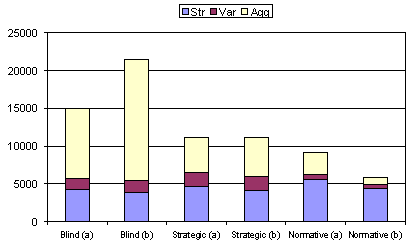
Figure 3. Results from table 2 shown in graphical form. The results denoted (a) are the original results; (b) show the replication results.
The “Str” column shows the total strength (energy levels) of all agents in the population. The “Var”[13] column gives a measure of inequality or variance between the agents in the population. The “Agg” column gives the total number of “attack” acts performed. Each of these columns gives an average based on 100 individual runs with identical parameters but different pseudo-random number seeds. The column to the right of each of these gives the standard deviation for the set of 100 individual runs. What do these results tell us? Firstly, general observations are given that hold for both sets of results and then replication differences are discussed.
Overall, populations composed entirely of agents following the norm (Normative strategy) produce higher levels of strength and lower levels of inequality than populations composed entirely of Blind or Strategic agents. As would be expected populations of only Blind agents produce the highest amounts of aggression and lowest amounts of strength since Blind agents always attack if they can. An all-Strategic population produces higher strength than all-Blind but lower equality. This is to be expected since strong agents are unlikely to be attacked in this scenario and hence the strong get stronger and the weak get weaker. The all-Normative populations therefore support a “more desirable” social group – in the sense that total strength is high and inequality is low.
The replication results (see table 2(b)) show much higher levels of aggression for the all-Blind case and much lower levels for the all-Normative case. The average strengths are somewhat lower in the replication results. Remember (as stated previously) that the assumption of instantaneous action was relaxed and therefore we expect to see differences. The results are similar to those obtained by a previous replication (Staller and Petta 2001). This is to be expected since they also relaxed the simultaneous action assumption. However, the further relaxation of assumptions (i.e. the random selection with replacement of agents for action during each cycle) means that the results do not match exactly those of Staller and Petta. However, the general observations hold for all variants of the model and this adds weight to the generality of the results – which should not be effected by implementation detail concerning synchronous / asynchronous action selection or sequential ordering.
3.2 Split Population Experiments
Table 3 and figure 4 show previous results (a) and replications (b) for mixed populations (i.e. where the population is split equally between agents exercising two different strategies).
Results are given with statistics split by strategy group, rather than for the entire population. In the context of strength levels (Str), Strategic agents outperform Blind agents, Blind agents outperform Normative agents and Strategic agents outperform Normative agents. However, the Normative agents produce a group with much lower levels of inequality (Var). The replication results show a similar pattern to those given in table 2, with the difference in aggression between groups being more pronounced, though strength levels being roughly comparable to the results from the previous model.
|
Table 3: Mixed population results |
||||||
|
a) Results from Conte et al (1995) |
||||||
Strategy |
Str |
st.dev |
Var |
st.dev |
Agg |
st.dev |
Blind
|
4142 |
335 |
1855 |
156 |
4686 |
451 |
Strategic
|
4890 |
256 |
1287 |
102 |
2437 |
210 |
Blind
|
5221 |
126 |
1393 |
86 |
4911 |
229 |
Normative
|
4124 |
187 |
590 |
80 |
1856 |
74 |
Strategic
|
5897 |
85 |
1219 |
72 |
3168 |
122 |
Normative
|
2634 |
134 |
651 |
108 |
2034 |
71 |
|
b) Replication results |
||||||
Strategy |
Str |
st.dev |
Var |
st.dev |
Agg |
st.dev |
|
Blind |
3586 |
282 |
1744 |
182 |
7993 |
569 |
|
Strategic |
4369 |
267 |
1701 |
131 |
2941 |
254 |
|
Blind |
5051 |
116 |
1472 |
111 |
7365 |
266 |
|
Normative |
3037 |
144 |
491 |
69 |
363 |
41 |
|
Strategic |
5384 |
96 |
1481 |
109 |
3800 |
164 |
|
Normative |
2800 |
136 |
482 |
84 |
320 |
36 |
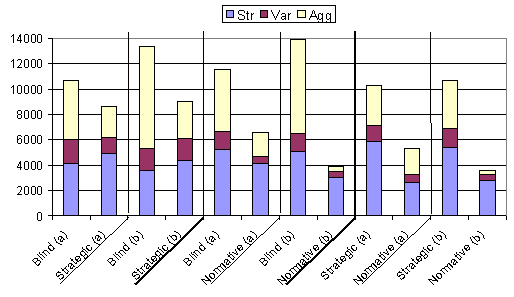
Figure 4. Results from table 3 shown in graphical form. The results denoted (a) are the original results; (b) show the replication results. Notice that since these experiments use mixed populations statistics for each strategy group are given separately for comparison.
4. Reputation and Communication
Results
As described previously (above), strategies were constructed which combined both reputation and communication of reputation with normative strategies. Given these mechanisms two further strategies were created:
- NormRep – Agents utilise the normative strategy but maintain a personal list of other agents’ reputation which is updated via direct interaction. Reputation takes the form of a binary flag signalling either a “cheater” who does not follow the possession norm or a “respectful” who does.
- NormRepCom – Agents follow the NormRep strategy but communicate their reputational information with their neighbours (assuming those neighbours are not flagged as cheaters).
Both strategies were compared by placing them in a mixed population equally split between agents operating a Strategic strategy and one of the augmented normative strategies (NormRep or NormRepCom).
Table 4 and figure 5 show the results (a) and replications (b) where NormRep and NormRepCom strategies are paired with the Strategic strategy within a population. Again in the context of strength the Strategic strategy outperforms both normative strategies. However, it is clear that the NormRepCom strategy (where reputation is communicated between agents) allows those following the possession norm to increase their strength against those operating the Strategic strategy. Also, the equality within the group of norm followers is substantially lower than the Strategic group.
It can be seen however, that the gap between the strength of the Strategic agents and the normative agents (with and without communication) is larger for the replication (section b) than for the previous results. It would seem that the random ordering and asynchronous action method erodes the advantages of reputation and communication of reputation[14].
|
Table 4: Reputation and communication results |
||||||
|
a) Results from Castelfranchi et al (1998) |
||||||
|
|
Str |
st.dev |
Var |
st.dev |
Agg |
st.dev |
|
Strategic |
5973 |
89 |
1314 |
96 |
3142 |
140 |
|
NormRep |
3764 |
158 |
631 |
101 |
1284 |
59 |
|
Strategic |
4968 |
309 |
2130 |
108 |
2417 |
227 |
|
NormRepCom |
4734 |
301 |
737 |
136 |
2031 |
253 |
|
b) Replication
results |
||||||
|
|
Str |
st.dev |
Var |
st.dev |
Agg |
st.dev |
|
Strategic |
5329 |
106 |
1563 |
116 |
3733 |
182 |
|
NormRep |
2870 |
152 |
496 |
75 |
379 |
58 |
|
Strategic |
4317 |
311 |
2299 |
113 |
2890 |
295 |
|
NormRepCom |
3880 |
321 |
711 |
152 |
1489 |
273 |
However, the essential observation from the previous work (Castelfranchi et al 1998) has been replicated, that the storage of social knowledge in the form of reputation of other agents reduces the cost that the possession norm places on followers. Additionally, if reputation is communicated between norm followers (a kind of “gossip”) then that cost is again reduced.
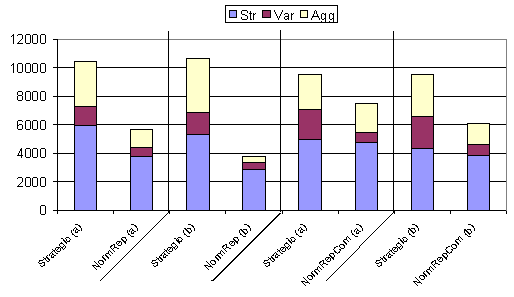
Figure 5. Results from table 4 shown in graphical form. The results denoted (a) are the original results; (b) show the replication results. Notice that since these experiments use mixed populations statistics for each strategy group are given separately for comparison.
5. Extending the Model with Group
Reputation
The model was extended to allow for reputation to be stored and communicated concerning whole groups of agents rather than individual agents. Instead of agents storing a flag against each other agent (specifying it as a “cheater” or “respectful”) agents pre-partition the population into a set of n equally sized groups. The partition may or may not be arbitrary (see later) but in either case, each agent only maintains a single reputation flag against an entire group – this means that a group containing a single “cheater” could gain the reputation of “cheater” that would then be applied to every member of the group. Essentially then, agents can be thought of as “stereotyping” all agents within a given group as behaving identically and this means that a single miscreant can discredit the entire group with other agents[15]. It is possible to consider the previous experiments (in which reputation was attached to individuals) as a special case of group reputation where the population is divided into n groups, where n is the population size, such that each agent is within a unique group.
It is important to realise that this minimal form of group reputation is not concerned with (and does not model) the emergence of groups or the emergence of group categories[16]. The population is partitioned a priori by all agents into a fixed set of n groups. All agents know which group all others belong to and share this as a kind of common knowledge. This can be visualised as each agent being marked with an unchanging colour that can be observed by all other agents. For a population divided into n groups we would have n colours (say, red, green, blue… etc) with each agent in the same group coloured with the same colour. Agents only store reputational information concerning a colour, rather than an agent.
5.1 Group Reputation Results
Table 5 and figure 6 show results obtained when the population of 50 agents is partitioned randomly into 10 groups (each containing 5 agents).
|
Table 5:
Partitioned into 10 groups (random) |
||||||
|
|
Str |
st.dev |
Var |
st.dev |
Agg |
st.dev |
|
Strategic |
4926 |
209 |
1920 |
172 |
3421 |
208 |
|
NormRep |
3116 |
210 |
1195 |
129 |
1654 |
170 |
|
Strategic |
4286 |
291 |
1971 |
132 |
2844 |
276 |
|
NormRepCom |
3820 |
299 |
1746 |
162 |
2400 |
264 |
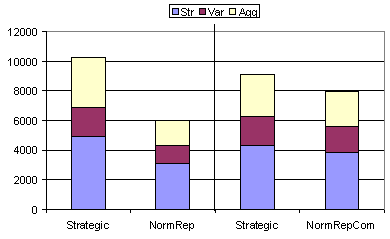
Figure 6. Results from table 5 shown in graphical form. Notice that, since these experiments use mixed populations, statistics for each strategy group are given separately for comparison. The thick black vertical line separates two independent experiments.
Each agent can only be identified by group membership and hence all reputation information is applied to a group rather than individuals. Other than the group allocations all other parameters are identical to those used for the experiments given in table 4(b). The results show a slight narrowing of the gap between strength levels between the Strategic and the normative agents but normatives still do worse (in the context of strength – Str) with and without communication. Since group membership is allocated randomly we would expect that most groups would contain Strategic and normative agents.
Given this, it will not take long for all groups to have a reputation as “cheaters” since it only takes on non-normative act by a group member to tar the group reputation permanently. When all groups are reputed as “cheaters”, the behaviour of all agents effectively becomes that of Strategic.
|
Table 6:
Partitioned into 10 groups (non-random) |
||||||
|
|
Str |
st.dev |
Var |
st.dev |
Agg |
st.dev |
|
Strategic |
4767 |
247 |
2158 |
154 |
3285 |
259 |
|
NormRep |
3416 |
267 |
588 |
108 |
1041 |
212 |
|
Strategic |
3906 |
326 |
2297 |
111 |
2459 |
304 |
|
NormRepCom |
4370 |
338 |
734 |
143 |
1874 |
271 |
Indeed if the values of both Strategic and normative groups in each of the two scenarios given in table 5 are combined the results are similar to those obtained in the all-Strategic scenario given in table 2. The differences result from the initial delay during which reputations are made and spread. We would therefore expect that if agents were allocated to groups based on their strategy (rather than at random) the stereotyping process would not simply breakdown the normative behaviour via the spread of bad reputation. Or put another way, what would happen if the stereotypes were grounded such that all agents within a group practiced the same strategy?
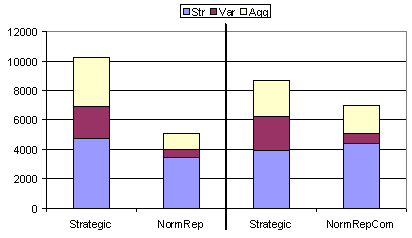
Figure 7. Results from table 6 shown in graphical form. Notice that, since these experiments use mixed populations, statistics for each strategy group are given separately for comparison. The thick black vertical line separates two independent experiments. Note that, in the results to the right of the line, the strength (Str) of the NormRepCom group is higher than the Strategic group.
Table 6 and figure 7 show results obtained when the 50 agents are partitioned into 10 groups (each of 10 agents in size) such that each group is strategy homogenous. This means that each group of 10 agents are either all Strategic or norm followers. As before the NormRep and NormRepCom represent normative reputation without and with communication respectively. Of particular interest are the relative strengths of the Strategic and NormRepCom agents. Notice that the NormRepCom agents (those agents operating the possession norm and practicing the communication of reputational information) actually outperform the Strategic agents. The NormRepCom manage this without compromising the previous normative profile of low inequality and aggression levels. This is an interesting and not entirely intuitive result. What is happening?
In the previous (non-group) experiments communication of reputation reduced the costs born by the normative group because each individual norm follower did not have to detect a “cheater” directly by incurring a cost. Once a single norm follower had been cheated it could communicate this information (bad reputation) to all other norm followers as they were encountered in the population. In this way a norm follower receiving information concerning the bad reputation of a cheater never need be cheated by it. However, this process required at least one norm following agent to be cheated by each individual cheater – so for each individual with a bad reputation, one norm following agent had to “pay” the cost of finding out this information by being cheated. The bad reputation was, in a way, a record of at least one past act of cheating by the individual agent.
However, when the domain of the reputation is expanded to cover an entire group of agents this means that only a single agent within a given group need cheat for the whole group to be labelled as cheaters. Consequently agents that have never cheated (or even interacted at all with) others may gain reputation as cheaters. When groups are homogenous, such generalisations are valid – only one agent need cheat to identify the entire group. In this way, norm followers can insulate themselves from the cheating of any other members of the group before they have a chance to act. Hence table 6 shows that within the artificial society gross stereotyping will benefit norm followers when the stereotypes reflect the object situation (when the stereotyping supplies predictive utility). It seems sensible to hypothesis that the more general such “grounded” stereotypes are the more beneficial they will be. To test this, the population was partitioned into just two groups. Each group contained all the 50 agents with a given strategy (Strategic and NormRepCom). The results are given in table 7 and figure 8.
Table 7 and figure 8 show an increase in the strength of the normative agents with and without communication over the results from table 6. Equality is still substantially higher for the norm followers. Note that the number of aggression acts increases over the results for 10 groups (given in table 6). Due to the gross stereotyping of the population into two groups, all agents within the Strategic group become labelled as “cheaters” after the first attack on a normative. The spread of this bad reputation between all the normative agents will take some cycles. But after this bad reputation has permeated the society, norm followers will effectively apply the Strategic strategy to all Strategic agents but the possession norm strategy to norm followers. In this way, the normatives insulate themselves from the cheaters. However, this process relies on the “grounding” of the stereotypes such that they correctly cover strategy homogenous groups. What happens if this arrangement is only slightly disturbed?
|
Table 7:
Partitioned into 2 groups (non-random) |
||||||
|
|
Str |
st.dev |
Var |
st.dev |
Agg |
st.dev |
|
Strategic |
4281 |
314 |
2324 |
121 |
2813 |
266 |
|
NormRep |
3960 |
294 |
667 |
136 |
1537 |
262 |
|
Strategic |
3730 |
373 |
2255 |
180 |
2312 |
339 |
|
NormRepCom |
4559 |
398 |
713 |
145 |
2025 |
306 |
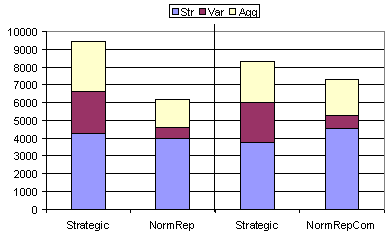
Figure 8. Results from table 7 shown in graphical form. Notice that, since these experiments use mixed populations, statistics for each strategy group are given separately for comparison. The thick black vertical line separates two independent experiments. Note that, in the results to the right of the line, the strength (Str) of the NormRepCom group is higher than the Strategic group (higher than in the 10 group case – shown in figure 7).
Table 8 and figure 9 show the results when one agent from each group is swapped such that the stereotyped groups are no longer strategy homogenous. Even this small element of “noise” totally breaks down the advantages that the normative group had when the groups were completely strategy homogenous. Why does this happen? Since it only takes one cheating act by a member of a group to give the whole group a bad reputation, both groups quickly become labelled as cheaters. In this condition all agents effectively become strategic players. With communication this process will occur more rapidly, but the effect will be the same. Interestingly, the faster convergence to the “total negative reputation” condition (produced by communication) benefits the normatives as a group, since they are less likely to be cheated individually.
|
Table 8: Partition
into 2 groups (one swap) |
||||||
|
|
Str |
st.dev |
Var |
st.dev |
Agg |
st.dev |
|
Strategic |
4374 |
292 |
2168 |
151 |
2937 |
301 |
|
NormRep |
3683 |
332 |
1351 |
252 |
2213 |
292 |
|
Strategic |
4146 |
334 |
1932 |
150 |
2666 |
307 |
|
NormRepCom |
3993 |
337 |
1791 |
184 |
2561 |
297 |
Here we see the duel nature of the kind of very general stereotyping represented in the simulation. When the stereotype is well grounded then this may be a method (when combined with communication) for agents practicing pro-social beneficent behavioural norms (in this case possession rights) to outperform more selfish “economically rational”[17] kinds of agent. However, when the stereotype is not grounded (even if only slightly wrong) then the same process leads to a totally breakdown of pro-social normative behaviour – even though half the population are initially norm followers.
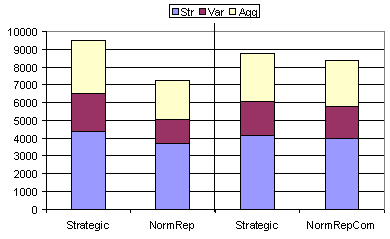
Figure 9. Results from table 8 shown in graphical form. Notice that, since these experiments use mixed populations, statistics for each strategy group are given separately for comparison. The thick black vertical line separates two independent experiments. Note that, in the results to the right of the line, the strength (Str) of the NormRepCom group is lower than the Strategic group (hence the advantage seen in figure 8 has disappeared).
As with the previous individual agent level reputation mechanisms, the mechanism of reputation communication implemented in the model follows a kind of “one-shot” process. Each agent assumes all other groups are non-cheaters (respectful) unless otherwise informed by experience or communication. Once a group is labelled as a “cheater” there is no way to reverse the negative label. Also there is the assumption that agents do not lie or communicate incorrect information. Given this latter assumption the “one-shot” mechanism appears reasonably plausible when reputation is stored at the individual agent level – one bad act by an agent tars the agent for life. However, for a group this appears rather strict – one bad act by a single agent tars the whole group for life. Given some set of groups, this process may have a knock-on effect.
Consider the situation in which the population is divided into a set of groups G over which all agents stereotype. Now suppose all agents are nomatives apart from one agent, located in group g (say). Now, if this agent cheats another agent, a (say) in group n, this agent will form the reputation that group g is a “cheating” group. If a then interacts with another member of group g (say agent c) which is a normative agent it will treat it as a cheater – even though it is not. This act will form the reputation within agent c that all members of group n are “cheaters”. Other normative agents will accept these negative reputations via communication based on which is received first. Remember that normative agents do not accept reputational information from those they considered being “cheaters”. In this sense the population contains mutually competing negative reputations. The only way a group x could avoid being viewed as a cheating group would be for no member agent m of x ever to cheat another agent p while it still had a good reputation with a significant number[18] of the rest of the population even if m believed p to be a cheater (based on its own reputational knowledge).
The agents modelled here have no such ability to reason about their own “group reputation” and therefore have no “group reputational management” strategies. However, it would seem that since the agents already operate cognitively with group categories themselves, they should be aware of their own group membership and develop strategies that take account of the way other agents perceive them. In this way, we can see how a socio-cognitive mechanism employed by agents (stereotyping) comes to produce objective social relationships between agents that dictate new kinds of behavioural strategies and cognitive structures. Such insights concerning social phenomena are, of course, not new. But what is new is the capture of such complex socio-cognitive feedback mechanisms at a high-level of detail and the objective formal representation (via a computer program) of the assumptions of the model.
As stated previously, the current model does not attempt to capture the emergence of groups over time, rather they are a priori assumed. The results presented here suggest that for beneficent norms to be beneficial to those who practice them groupings are required to be grounded – that is – that some form of categorisation of individuals need to offer predictive utility concerning those individuals possible future behaviours. Recent tag models have demonstrated how such groupings can emerge endogenously from (cultural) evolutionary processes based on imitation of the more successful agents. However, the tag models, up to the present, generally ignore cognitive and spatial aspects – representing agents as no more than very simple reactive units interacting in mean-field clouds. Future work will examine the possible role of tag processes at this higher cognitive agency level – in emerging and structuring groups that can support beneficent norms with a cultural evolutionary scenario.
6. Conclusions and Future Work
The results presented here show that group-level reputation, when stored and communicated between agents can have a dramatic effect on the relative performance of normative agents who respect a possession norm and cheating agents that do not. Specifically, the group of norm followers can, given the right conditions, outperform the cheaters by spreading “negative stereotypes” in the form of group reputations that indicate a whole group of agents are cheaters. However, in different conditions the stereotyping mechanism almost completely negates any socially beneficent behaviour.
These results are significant because they demonstrate the potential power of stereotypes for both the support and negation of socially beneficial norms. It begins to address the socio-cognitive interplay that produces certain kinds of social behaviour and identifies conditions under which support and negation of the norm will occur. Also it has been demonstrated that as the size of the any stereotyped group is increased (i.e. a stereotype being more generally applicable), the potential utility of stereotyping is increased but the chances of misclassification also increase. In this sense the stereotyping process is a “double edged sword” either potentially promoting socially beneficent norms or negating them. It is argued that a rigorous understanding of the conditions which select between these edges would be a worthy research enterprise in both human and artificial systems.
Agents practicing the socially beneficent norm only outperformed cheaters in scenarios where the groups contain strategy homogenous agents – that is, when stereotypes can perfectly match the objective distribution of strategies in the population. The work here has not address the emergence of groups or group level reputations. Currently agents are not allowed to join and / or leave groups or revise their reputational information in the light of new information (in the current model, once an agent or group has a bad reputation it can not be reversed).
One line of future work would involve addressing (at least some) of these issues. Previous work with less sophisticated agents in simpler environments (Hales 2000, Hales 2001, Riolo 2001, Hales 2002a, 2002b) has demonstrated that evolving agents with recognisable social cues (so called “tags”) can self-organise into relatively homogenous, cooperative groups. If other agents stereotyped agents sharing the same or similar tags then it might be possible for norm following groups to emerge and become successful within the population. However, this requires implementing an evolutionary process within the population. We would envisage that such a process would follow a memetic (Hales 1998a, Flentge et al 2001), rather than genetic rubric.
The model demonstrates a complex interplay of spatial and informational dynamics – retaliation against a group could cause a norm follower in the group to spread bad reputation about that group from which the retaliation came. As stated previously, these kinds of issues lead on to a whole set of possible second-order strategies that might be termed “reputation management” strategies. Such strategies can involve behaving in a counter intuitive way, such as letting known cheaters cheat again, depending on the beliefs of others concerning the cheaters. It would seem that highly complex strategies might evolve if agents are given the ability to induce such “reputation management” rules. Future work could explore different reputation management strategies.
It would also appear that spatial dynamics are important in this model – since interaction and reputational spread are spatially mediated. The experiments so far have distributed group members randomly over the grid – but what would happen if those sharing a group tended to be spatially clustered? Would this benefit a group or hinder it? Again, several issues involving spatial clustering of groups could be studied in future work.
Even with the very minimal representation of group reputation presented here, very significant effects are produced on agent behaviour and dynamics compared to the effects of purely individual reputation. Competitive interaction combined with the cognitive ability to handle social concepts of group and reputation, combined with communication (i.e. gossip) appear to form a tight linkage in the production of a kind of “group rationality”[19] that promotes “groupish” behaviour (Ridley 1996). The concept of “social rationality” (Kalenka and Jennings 1999) has been raised within the Distributed Artificial Intelligence (DAI) community as a solution to selfish agent behaviour producing suboptimisation within engineered agent systems. Future work could extend these simulations in order to find the kinds of reputational mechanisms agents need in order to protect themselves from errant or malfunctioning “non-socially rational” agents – which are bound to occur in any open agent system.
As stated previously, the results and experiments presented here are purely in the artificial domain. However, tentatively, the work suggests a rather negative and depressing implication for hypotheses applicable to real human societies. We might speculate that historically, groups which practice gross stereotyping[20] can prosper in certain circumstances but that this is precarious and can lead to a wholesale breakdown in pro-social norms if only a very small minority of agents behave in a non-conformist way.
Acknowledgements
This work was completed during an extended visit to the IP-CNR (Rome) from September to December 2001. I would like to thank those at the IP-CNR who made this visit possible and provided guidance, help, support and friendship. Particular thanks go to Rosaria Conte and Mario Paolucci who provided all the answers to my questions concerning the original model (on which the work in this paper is based) and helped me to refine my ideas about groups, norms and agents. Additionally I would like to thank the CPM (Manchester) for the flexibility given to me in allowing this visit to take place.
Appendix 1
The simulation software was implemented in JAVA2 using the Sun JAVA2 SDK 1.3.1. The software, both source and executable, will shortly be available at: http://www.davidhales.com/normsim.html.
References
Castelfranchi, C., Conte, R., Paolucci, M. (1998) Normative reputation and the costs of compliance. Journal of Artificial Societies and Social Simulation 1(3), http://www.soc.surrey.ac.uk/JASSS/1/3/3.html
Conte, R. and Castelfranchi, C. (1995) Understanding the functions of norms in social groups through simulation. In Gilbert, N. and Conte, R. (Eds.) Artificial Societies - The Computer Simulation of Social Life. London: UCL Press. pp. 74-118.
Conte, R. and Paolucci, M. (2002) Reputation in Artificial Societies. Social Beliefs for Social Order, Kluwer.
Flentge, F., Polani, D. and Uthmann, T. (2001) Modelling the Emergence of Possession Norms using Memes. Journal of Artificial Societies and Social Simulation 4(4), http://www.soc.surrey.ac.uk/JASSS/4/4/3.html
Hales, D. (1998a) An Open Mind is Not an Empty Mind - Experiments in the Meta-Noosphere. The Journal of Artificial Societies and Social Simulation 1(4), http://www.soc.surrey.ac.uk/JASSS/1/4/2.html
Hales, D. (1998b) Artificial
Societies, Theory Building and Memetics. Proceedings of the 15th
International Conference on Cybernetics, International Association for
Cybernetics (IAC), Namur: Belgium. Available at: http://www.davidhales.com
Hales, D. (1998c) Stereotyping, Groups and Cultural Evolution. In Sichman, J., Conte, R., & Gilbert, N. (Eds.) Multi-Agent Systems and Agent-Based Simulation. Lecture Notes in Artificial Intelligence 1534. Berlin: Springer-Verlag. Available at: http://www.davidhales.com
Hales, D. (2001) Tag Based Cooperation in Artificial Societies. Unpublished PhD Thesis. University of Essex. Available at: http://www.davidhales.com/thesis
Hales, D. (2002a) The Evolution of Specialization in Groups. To be presented to the RASTA'02 workshop at the AAMAS 2002 Conference. To be published by Springer
Hales, D. (2002b) Evolving Specialisation, Altruism and Group-Level Optimisation Using Tags. To be presented to the MABS'02 workshop at the AAMAS 2002 Conference. To be published by Springer.
Hobbs, T. (1962) Leviathan, Fontana. Available at: http://www.orst.edu/instruct/phl302/texts/hobbes/leviathan-contents.html
Hegselmann, R. and Flache, A. (1998) Understanding complex social dynamics. A plea for cellular automata based modelling. Journal of Artificial Societies and Social Simulation 1(3), http://www.soc.surrey.ac.uk/JASSS/1/3/1.html
Jennings, N. and Campos, J. (1997). Towards a Social Level Characterisation of Socially Reponsible Agents. IEE proceedings on Software Engineering, 144(1):11-25.
Kalenka, S. and Jennings, N. (1999). Socially Responsible Decision Making by Autonomous Agents. In Korta, K., Sosa, E. and Arrazola, X., (eds.), Cognition, Agency and Rationality. Kluwer.
Kramer, R. and Brewer, M. (1984). Effects of Group Identity on Resource Use in a Simulated Commons Dilemma. Journal of Personality and Social Psychology. 46(5), pp. 1033-1047.
Moss, S. (2002) Policy analysis from first principles. In Proceedings of the U.S. National Academies of Science, Vol. 99, Supp. 3, pp. 7267-7274.
Oakes, P. et al. (1994) Stereotyping and Social Reality. Blackwell, Oxford.
Ridley, N. (1996). The Origins of Virtue. Penguin Books, London.
Riolo, R., Cohen, M. D. & Axelrod, R. (2001), Cooperation without Reciprocity. Nature 414, 441-443.
Saam, N. and Harrer, A. (1999) Simulating Norms, Social Inequality, and the Functional Change in Artificial Societies. Journal of Artificial Societies and Social Simulation 2(1), <http://www.soc.surrey.ac.uk/JASSS/2/1/2.html>
Shoham, Y. and Tenneholtz, M. (1992) On the synthesis of useful social laws for artificial agent societies (preliminary report). In Proceedings of the AAAI Conference. pp. 276-281.
Staller, A. and Petta, P. (2001) Introducing Emotions into the Computational Study of Social Norms: A First Evaluation. Journal of Artificial Societies and Social Simulation 4(1), <http://www.soc.surrey.ac.uk/JASSS/4/1/2.html>
Walker, A. and Wooldridge (1995) Understanding the emergence of conventions in multi-agent systems. In Proceedings of the International Joint Conference on Multi-Agent Systems (ICMAS) San Francisco.