To the Outer Limits and Beyond
– characterising the envelope of sets of social
simulation trajectories
Bruce Edmonds*, Oswaldo Terán#*, and Gary Polhill+
*Centre for Policy Modelling, http://bruce.edmonds.name
#University of Los Andes, http://cfpm.org/~oswaldo
+Macaulay Institute, http://www.macaulay.ac.uk
1 Introduction – the problem
Social simulations explore the formal possibilities inherent in a computational model of social phenomena or, more usually, an abstraction of some social phenomena (Edmonds 2001). That is, the sequence of states in a single run of a simulation is one possible ‘trajectory’ consistent with the rules or program that specifies the computation – each run is a possible ‘unfolding’ of consequences of the simulation program. Some of the specification of that program will encode a prior knowledge concerning the mechanism and relationships, and other parts will have been added merely to get the simulation to run. Some aspects of the resulting trajectories will be deemed significant in terms of the modelling target and others as essentially arbitrary (e.g. simulation ‘artefacts’). What is of interest is: the causal connection between the representative part of the specification and the significant aspects of the resulting simulation trajectories (Edmonds 2005). Thus we are typically interested in the collection of such runs – the ‘set of trajectories’.
In simple simulations (sometimes called ‘linear’ models) it is often sufficient to characterise such sets using aggregate measures of a random sample of the trajectories, e.g. the average and standard deviation of a measure (or set of measures) on the trajectories. In more complex simulations (sometimes called ‘nonlinear’ models) this can be inadequate, as simple measures do not reveal the structure of the set of trajectories, and for many purposes it is the structure that is the most interesting (and thus part of the significant aspects of the results).
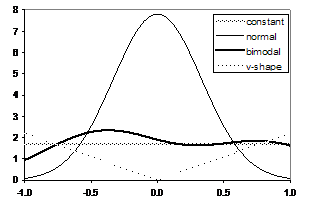
Figure 1. Three distributions (restricted to [1, -1]) with the same mean (0) and standard deviation (1).
For example Figure 1 above shows four distributions (a constant, normal, bimodal and v-shaped distributions restricted to the interval [1, -1]) which share the same mean and standard deviation (0 and 1 respectively). If a researcher were to plot the mean with standard deviation error bars of three sets of simulation runs, where each happened (due to the internal dynamics) to have a constant, normal and bimodal distribution of outcomes then that researcher might miss an important result which might be significant in terms of the target phenomena.
A different response to the problem of characterising sets of simulation trajectories is to display them all or (more practically) some aspect of them all. In other words, to avoid summarising the data as much as possible. Thus in the model of domestic water demand and social influence (Edmonds and Moss 2005) for each set of parameters the aggregate water demand was shown, as in Figure 2 above (corresponding to figure 4 in (Edmonds and Moss 2005)). Looking at these one gets some idea about the variations between runs that are possible as well as, conversely, what might be common to all runs. If one compares the set of trajectories in Figure 2 with those in Figure 3 (where a single parameter was changed) one can see that, despite the variations between the trajectories within a set, collectively they differ markedly from the second set.
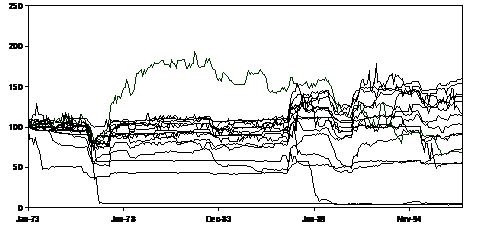
Figure 2. The relative aggregate water demand in 14 runs of a model (Edmonds and Moss 2005) with the same parameters (scaled so that 1973=100). Here the neighbourhood for the influence is of size 24.
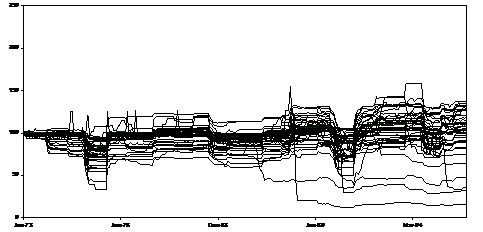
Figure 3. The same as Figure 2 above but for 24 runs of the model for neighbourhoods of size 4.
In this model it seemed (under some conditions) to exhibit self-organised criticality (Bak 1997; Barthelemy forthcoming). For this reason one may expect that the distributions that result from the model might not have well-defined moments as the sample size tends to infinity. Although the particular sets of trajectories will have well defined standard deviations (due to the fact they are a finite sample), these may be more artefacts of sample and model size than representative of the target phenomena. Simply exhibiting the sets avoids introducing such artefacts.
The problems with this approach are (at least) two-fold:
● Whilst the approach gives the researcher information about some of the possibilities inherent in a model, one can never be certain that, if one did more runs, one might discover a new kind of trajectory. Thus one never knows when one has done enough runs of a model.
● This only gives a set of particular examples of what might happen, it does not (of itself) allow one to generalise about what is common to all possible outcomes. This relates to the traditional criticism of those who prefer analytic models to simulation models: simulations are ‘just’ numerical examples.
These lead us to another approach to characterising sets of simulation trajectories: that of their ‘outer envelope’. This outer envelope of trajectories can be thought of as the boundary ‘surface’ (in some space of relevant aspects[1]) that (a) includes all possible trajectories (no trajectory crosses it), but (b) is minimal (there is no different surface between it and the trajectories that also satisfies condition (a)). Intuitively if one thinks of each trajectory as a fibre, so that the collection of trajectories is a bundle of such fibres, the envelope would be a tight skin around the bundle. This idea is suggested in (Teran, Edmonds et al. 2001). Figure 4 is an example of this.
Thus the problem addressed by this paper is:
how can we go about characterising this envelope?
If we could characterise such an envelope this would be a general condition that is true of all outcomes of a particular simulation set-up – this would be a general result concerning the simulation behaviour comparable to the closed-form solutions of analytic models. It would answer some of the criticisms of simulation models by eliminating some of the uncertainty introduced by their use, and thus help to establish social simulation as a science. It only provides limited information about the whole set of trajectories, in particular it does not say anything about the probability of particular trajectory routes (which can be thought of as the ‘density’ of the fibres). Thus if a simulation was purely probabilistic, so that anything could occur, (just vanishingly unlikely to do so in many cases) this approach would not be very informative. However, this approach could provide certain information and should be used in conjunction with other ways of characterising the set of trajectories.
2 Some possible approaches – from the inside and the outside
Of course, we already have one method of approaching the envelope from the inside – normal simulation. Each simulation trajectory resulting from a run of the model is an inner limit to the envelope (by definition). Thus if we have observed enough trajectories we may hypothesise an outer bound for the envelope – this is a general hypothesis about all possible simulation outcomes. Every time the simulation fails to falsify this hypothesis we might have (slightly) more confidence in it. In this way, just as in mainstream experimental science, we might progress via the accumulation of fallible knowledge. Here loose bounds on the envelope are weak hypotheses whilst tight ones are strong hypotheses. Very loose hypotheses are of little use (e.g. that anything can happen) but easy to demonstrate; tight hypotheses are of more use (e.g. in 2007 a horse called Chaotica will win the Grand National) but difficult to establish. Of course, it may be that loose bounds are all that can be established.
The trouble with this method is that it only gives us negative knowledge: a lack of refutation of an outer bound for the envelope. Whilst in the real world this is usually the only kind of knowledge that is available, simulations and their specifications have special properties – they are formal objects[2] obeying precise, definable rules. Whilst this does not mean that most questions about them can be definitely settled, either in practice (due to the complexity of finding their proof) or in theory (due to the results of Gödel et al.), it does open the door to other approaches that provide more definite information about the envelope.
The most straightforward approach is to try all possible trajectories and check that an outer bound holds for each. This is the approach in (Teran 2001), whereby all price trajectories are automatically checked in a branching model over a limited number of time periods. Of course, whilst this is useful for checking models with a limited number of trajectories, it has a severe computational complexity and is completely impossible where the branching is not finite (e.g. where random floating point numbers are used).
A second approach is to translate the simulation program into a set of logical axioms and then use automatic theory proving techniques to attempt to prove general properties about the simulation outcomes. This is difficult with a typical social simulation model because of the complexity of the models and the expressiveness of the language they are written in. That is, these typically involve the representation of many individuals involving the unbounded arithmetic. The many individuals mean that any inference will be quite complex as the point about separately representing individuals is that each may involve different decisions depending upon their different states, and so any inference will either have to trace these different possibilities or generalise across common properties (which is difficult). The use of arithmetic makes complete theorem proving impossible.
A third approach can be thought of as a combination of the first two and is broadly called “constraint logic programming” (CLP) (Marriott and Stuckey 1998). CLP is a combination of declarative programming (as in Prolog) and constraint satisfaction programming, where one specifies a set of constraints and the computer seeks a solution to these constraints. Efficient constraint satisfaction algorithms ‘propagates’ constraints – inferring new constraints to restrict the search space. CLP aims to exploit the synergy between bottom-up, backward-chaining, logic-programming inference and top-down, forward-chaining constraint propagation.
If we know some constraints on the simulation set-up then we may be able to deduce other constraints from these, possibly including a useful outer bound for the envelope of trajectories. Thus each chain of deduction from the initial constraints might add a new outer bound, thus allowing us to approach the envelope from the ‘outside’. In this case we would have a method of approaching some inner as well as outer bounds to the envelope – ‘pincering’ to allow us to characterise it more precisely.
Before a practical approach to this is outlined in the next section, there are some limitations to point out. Firstly, it is unlikely that (in all but the simplest of systems) that it will be possible to obtain the theoretical envelope of the trajectories – this would be akin to proving that a running program precisely matched its specification (which for most[3] classes of program) is known to be impossible in general (Edmonds and Bryson 2004). Instead we will have to be satisfied with differing inner and outer bounds for the envelope. Secondly, to reiterate that there will be no proof method that will guarantee to either come up with a proof of a specified statement or that no such proof is possible. Rather we will have to settle for incomplete methods – those that may come up with a proof but may fail even when a proof exists. Finally, there is always the temptation to over-simplify models. The danger in this is that the complete chain of inference that can be used to reason about the target phenomena may be weakened, even though the inference within the model is strengthened. As (Hesse 1963) describes there are (in the simplest version) three stages in using a model: (1) the interpretation of that phenomena into the initial conditions on the model; (2) inference using the model from those conditions to the significant results; and (3) the interpretation of those results back to the target phenomena as predictions or explanations. Simplifying a model may strengthen stage (2), but if this also involves making the model more abstract (which it almost always does) this will weaken stages (1) and (3) and hence the whole chain. This is a major problem with analytic models – the inference within the model is strong, giving closed-form solutions but, in the case of complex phenomena, this is often at the cost of introducing drastically unrealistic assumptions, resulting in a solvable abstract model which has lost its relevance to the target phenomena[4].
3 A structured approach to social simulation
In this section I describe an architecture for such an approach that can help attack the problem of characterising the envelope of trajectories. It is also compatible with the goals of the open comparison of sets of trajectories as described in (Edmonds 2003); with facilitating the important distinction between motivated and pragmatic parts of a simulation set-up as described in (Edmonds 2005); as well as aiding in the checking and comparison of models (Hales, Rouchier et al. 2003).
A model’s specification is separated into different parts, reflecting the different roles that each plays:
● A specification of the fixed structure of the model (the fixed structure or FS). These are akin to the declaration of variables in typed languages and are helpful because they implicitly indicate the possible values each can take. This might also include the structure of agents, within agents and the temporal structure. The structure is usually imposed by the modeller based on how they view the target phenomena, i.e. largely in the realm of a priori knowledge but informed by knowledge of the phenomena.
● Constraints on the model trajectories (the active constraints or AC). These are a set of active constraints on what is acceptable (on the basis of knowledge of the modelling target) in terms of solution trajectories. If one of these constraints were violated this would indicate the trajectory was not one of those intended by the modeller. This might include the specification of acceptable value for parameters, or expressing structural certainties implicit in the modelling target (e.g. only one agent has the parcel).
● Logical relations between components of the model (the logical relations or LR). These indicate the fixed relations between the parts of the model in deterministic ways (e.g. accounting rules, or the effects of an action). These are largely derived from knowledge of the target system.
● A set of generative rules including non-deterministic branch points (the generative rules or GR). These generate the possibilities within the constraints, which would include points where random numbers/choices are made (or where floating point operations are performed). These are often not representative, in that they stand for parts of the target phenomena which are either unknown or considered unimportant.
● Extra constraints to aid model solution (the extra constraints or EC). Often in constraint programming the addition of even redundant constraints (ones that the programmer knows will be respected anyway due to the other constraints) greatly aids the constraint satisfaction process by making the propagation of constraints easier. To check whether these are, in fact, redundant one, can try the system without the constraints to see if the results change. There is no difference between EC and SC in implementation terms, however keeping them separate aids model understanding and manipulation.
● Checking constraints including system checks and hypothesised outer bounds for the envelope (the checking constraints or CC). These are constraints that, if violated, generate an error message and stop the computation. These could either be checks against bugs in the model or hypotheses of outer bounds that are being experimentally tested against generated simulation trajectories.
These parts are conflated in most simulation work, so that it is often not made clear which parts are representative and which are merely necessary for implementational reasons. Such a structure allows for the development of simulation models as follows (these and the parts above will be illustrated in 4).
1. The specification of the fixed structure (FS) is primary and determines the items and referents which will be used to build the rest of the structure. This is ideally reflective of the structure of the target phenomena (this being the point of individual- or agent-based simulation), but is inevitably also determined by the purposes and conceptions of the modeller. It is here that the most basic assumptions are made, and hence it is most important that these are transparently declared and documented. For example these might be obtained from a formally-defined ontology of relations agreed between a modeller and a domain expert.
2. Next comes the specification of the logical relations (LR) and active constraints (AC) – these should be representative of the target phenomena (or, at least, of what is thought to be representative). These constitute what is thought of as the core programming of a simulation, but in a declarative manner. FS, LR and AC should together specify what are acceptable simulation trajectories; that is, a set of properties consistent with FS+LR+AC should be a possible trajectory and FS+LR+AC should allow all such trajectories. In an ideal system one could obtain possible trajectories that are consistent with FS+LR+AC at this stage (albeit in a very inefficient manner) without further programming using a suitable algorithm.
3. The generative rules (GR) define the way the trajectories branch; in other words how the trajectories might be generated/searched in a positive manner. Ideally these should work synergistically with the constraint propagation in order that the simulation may be run efficiently. They may also ensure that the possible trajectories are generated in a representative manner, e.g. by specifying the order of choices or the distribution of numerical choices. This does not affect the shape of the envelope, but that is only one way of characterising the set of trajectories – the ‘density’ of trajectories will be largely determined by the GR.
4. A number of extra constraints (EC) may be added. These should be logically redundant but greatly aid the inference engine to propagate constraints. One should check that adding these does not change the set of results that are produced (although it is possible that results may be produced in a different order).
5. Checking constraints (CC) may be of (at least) two varieties: checks and hypotheses. Checks are like EC in that they should be always obeyed anyway. They are added to help ensure that no mistakes are made in the programming of the simulation. These may be added or removed depending on whether one is debugging or doing final simulation runs. The hypotheses may be added to (experimentally) determine whether they are true of the simulations runs as described above.
The simulation platform should ensure that the constraints LR+AC+EC are respected, and GR+LR used to compute/choose the possible trajectories. Using Constraint Logic Programming, LR+AC+EC should be propagated in parallel to generating the possibilities using GR+LR, using the result of each to inform the other (this is the ideal). Whilst it is doing this it should be constantly checking the CC and throwing an error if any of these are violated. Preferably the set of consistent trajectories that are produced by the system would be held in a database of standard format so that a variety of different tools (e.g. Mathematica and visualisation tools) could be used with it as suggested in (Edmonds 2003). For maximum flexibility the above program specification should also be held in a standard format so that different inference engines could be used upon it.
4 A demonstrator system
Clearly the CLP approach is not useful for either a purely deterministic or purely probabilistic model. In the former case there will be no branching, one could just run the simulation to see what happens. In the later case anything could happen and so one will not learn much via logical inference. Rather it will only be useful where one has a model with a mixture of deterministic rules and constrained non-determinism. In this section I summarise my experience with a demonstration model which we have been using to explore some practical ways in which the above suggestions could be implemented.
I have chosen a game with social elements for the demonstration model: the game called ‘liar dice’. The game is played between a fixed number (np) of players with a fixed number of normal, 6-sided dice (nd). Play is done in turns round the players in a fixed order. The current player has the dice, keeping them hidden from the other players. This player may roll any or none of the dice (everyone sees how many are rolled); then makes a claim about the dices’ total (which may or may not be true) which must be higher than previous claims in a single game. The next player then chooses whether to accept the dice or challenge the claim. If they accept the dice they play. If they challenge the dice are revealed – if the claim is greater than the dice total the challenger wins, otherwise the player wins. I am unaware of any specific studies about play in this game, but clearly people utilise a variety of strategies. It is a natural context in which to consider issues of reputation, recursive opponent modelling, and attitudes to risk. One might reasonably ask, in the absence of reliable knowledge about the cognition of players, whether any constraints concerning strategy (for example, not lying unless one needs to) has any general consequences in terms of resulting patterns of play. Ideally one would wish to be able to find answers to this question without having to impose a particular cognitive mechanism that, although consistent with the constraint, arbitrarily imposes arbitrary or uncertain features upon the process.
The parameters are: np = number of players (2); and nd = number of dice (5). Let PL={1,…,np} be an enumeration of the players; DI={1,…,nd} be an enumeration of the dice; DV={1, …,6} be the dice values; and T, F be the Boolean constants: true and false. There are the following predicates, where a,pÎPL, dÎDI, vÎDV, x is an integer, and bÎ{T, F}: T(p) – it is player p’s turn; D(d,v) – dice d have value v; B(x) – the current bid is v; C(b) – it is b that there is a challenge; R(d,b) – that if is b that dice d has just been rolled; N(a,p) – after a’s turn is p’s; and P@t – P is true at time t. Plus derived predicates S(x) iff the sum over dice of the values v in D(d,v) is x; and W(a) – player a has won.
The specification of the game (using a logical language) is: T(1)@1 (first player starts); T(p)ÙC(F)@t®T((p mod np) + 1)@t+1; (next turn if no challenge); T(p)@t®N(p,(p mod np) + 1)@t (next player); (R(d,F)ÙD(d,v))@t® D(d,v))@t+1 (unrolled dice stay the same); B(x)@tÙB(y)@t+1®y>x (bids must increase); B(6´nd)@t®C(T)@t (maximum possible bid forces challenge); T(a)@tÙN(a,p)ÙC(T)@tÙB(x)@tÙS(y)@t®(y≥x®W(a) Ùy<x®W(p)) (winning).
This game was further restricted by some additional constraints, which one might plausibly be derived from interviews with real players (but weren’t) – unlike detailed cognitive mechanisms which are not normally possible to directly elicit. These were that: players only rolled the dice if the last bid was not less than the current dice total; if they did need to lie (even after rolling the dice) they choose the minimum possible lie or one bigger than this (unless it was at the maximum possible bid or one less in which case they chose the minimum possible); the first bid was either the dice total or one bigger. There were two versions of the model: a procedural one and a CLP version.
Here the AC is straight-forward: fixed players; numbers of dice; sequence of turns; etc. The LR are: summing the dice; whose turn is next; that a maximum bid forces a challenge; that unrolled dice keep their value; and the rules for who has won a game. The AC include: that bids must increase; the possible dice values; that players do not lie if they don’t need to; that if they do lie they don’t claim more than 1 greater than the minimum possible bid. In the procedural version the GR include random number choices for dice and possible bid values, and whether to challenge, there are no GR in the CLP version (this is the point). EC in the CLP version included bounds on how much the dice total could change given the number of dice rolled. CC included the hypothesis about the outer bound as below and, in the procedural version: checks that bids occurred each term; dice only had one value each; that if there is a challenge someone has to win etc.
Under these rules Figure 4 shows a random sample of 10000 trajectories of the bid values for each turn in a game. From this it might be hypothesised that bids are easily at least 2(1+turn number).
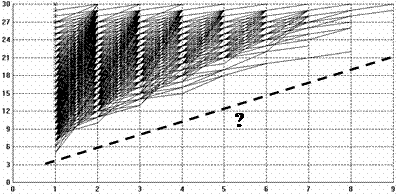
Figure 4. 10,000 trajectories of the bids against turn in the ‘restricted’ liar game, the dashed line represents an hypothesised outer envelope of the bid trajectories
However querying a CLP version of this model reveals that this is not the case – for example there is a game trajectory with bid sequence: 5, 6, 7, 8. This is a possible sequence, simply highly unlikely. To discover this counter-example using random sampling one would need a very large sample size! Of course, this conclusion is easily checked with only a little thought about the nature of the game, but the purpose of the example is to illustrate the approach. On the other hand the CLP version does indicate there is no trajectory less than (4+turn number), at least up to 4 turns.
The procedural version of the model was very straight forward, it is written in SDML (Moss, Gaylard et al. 1998). The CLP version was written in SWI-Prolog using Constraint Handling Rules (CHR) (Fruhwirth 1998; Schrijvers and Demoen 2004) to specify and then query the constraint propagation and rules. CHR are committed-choice, guarded, multi-headed, forward-chaining rules that are used to make general inferences about constraints (what is called ‘constraint propagation’) which results in a store of simple constraints that the underlying system (in this case Prolog) uses to search for possible ‘unfoldings’ of the specification. Thus this is supposed to help more efficiently constrain the search space of possibilities. The CHR system is available in several base languages, including: various Prologs; Haskell, and Java. For more information about CHR see the URL: http://www.cs.kuleuven.ac.be/~dtai/projects/CHR/ which includes many papers, examples and a web-interface where you can try them out. There is not room to give a complete description of the programs described in this paper not to mention the CHR system, but the simulation codes are available from the first author.
5 Related work
This work is an extension of that reported in (Teran 2001; Teran, Edmonds et al. 2001; Teran and Edmonds 2004). In that work SDML was used as a platform for flexible constraint programming using a combination of non-deterministic choices, forward-chaining rules and backtracking on constraints. The approach was made substantially more efficient using the “meta-rule” features of that language in order to ‘compile’ generic rules and constraints in to specific versions so that back-tracking occurs at the earliest possible stage. This technique was demonstrated on a simple simulation of suppliers, trucks and distributors, with price decisions.
Luis Izquierdo, Nick Gotts and Gary Polhill of the FEARLUS project at the Macaulay Instituted have been using a combination of analytic and simulation techniques to gain a richer understanding of behaviour in systems of repeated games, for example (Izquierdo, Gotts et al. 2004). The analytic analyses result in some general properties of the systems (e.g. asymptotic properties), whilst the simulations give an idea of the distributions and dynamic behaviour. The analytic model act as a check on the simulation, so we can have greater confidence in it, and the simulations allow for the exploration of the behaviour in elaborated versions of the game. Recently Luis has been using GRID technology (at Aberdeen University) to explore very large samples of behaviour and Gary has been exploring the use of formal ontologies to constrain (and/or help generate) simulation code.
There have been many approaches which seek to prove (or
verify) the properties of multi-agent systems from a formal logical
specification. Mostly these do not get near to proving anything very useful.
However in
(Engelfriet, Jonker et al. 2002) this is done for some simple properties by decomposing the system into a series of layers each of which ‘supervenes’ on lower levels.
Jim Doran has suggested that the understanding, checking and general formal manipulation of simulations may be facilitated by their compilation into a finite-state production system (Doran 2005). Whilst it is true that if such compilation were feasible then these desired benefits would be achievable, the feasibility of compilation for credible social simulations has yet to be established (I suspect the computational complexity is severe).
Yasser Ibrahim has been developing techniques that allow for the automatic or semi-automatic simplification of social simulations (Ibrahim and Scott 2004; Ibrahim 2006). By exploiting information about the dependency of rules in the simulation program the system is able to analyse and then simplify such programs with respect to specified goals and contexts. Thus if one is only interested in a certain aspect of the resulting behaviour (and we are rarely interested in all aspects) then this approach has been shown to work in some cases.
(Miller 1998) describes an algorithm to intelligently probe for key weaknesses in a simulation's structure. This algorithm incrementally changed the Club of Rome’s system dynamics model parameters within a 15% bound to search for the maximum change in endogenous variables, i.e., implemented an “intelligent” (goal directed) automated sensitivity analysis. The paper showed that the model was highly sensitive to parameter changes and hence played a roll in discrediting the model.
6 Concluding Discussion
There is no magic technique for effortlessly generating relevant certain knowledge, either about the world or complex social simulations. There will always be a complicated trade-off between: the complexity of a model; the feasibility of its computation; the generality of the conclusions obtained; and the skill of the investigator. It is important that models are not made unrepresentatively simple merely in order to make the inference of general conclusions about the simulation feasible – this would be to overvalue the importance of the model as compared to the phenomena it is supposed to be representing. That route leads to a world of ‘toy models’ and, ultimately, irrelevance to real issues.
However, in social simulation there is much in simulation programs that is there not there to represent any aspect of observed phenomena but present only to get the simulation to run. In such cases if we can reduce such arbitrary aspects and still obtain some results, we may avoid some simulation artefacts allowing the significant aspects of simulation outcomes to become clearer. The techniques suggested in this paper could thus allow for the simultaneous simplification of simulations with improving their representative validity (at the cost of the expenditure of more computational resources).
Furthermore, the use of explicit constraints upon our simulation models could improve their reliability, reduce the incidence of unintended bugs, aid the documentation of modelling assumptions, and facilitate model comparison. A criticism of individual- and agent-based simulation is the freedom that modellers have to get the results they desire, by choosing to constrain our own modelling we can answer this criticism, and may gain additional information about our own creations in the process.
Acknowledgements
Thanks to all those who have commented upon this paper, particularly Rodolfo Sousa who informed me about the ANTs stuff, but also including: Emma Norling, Ruth Meyer, Bogdan Werth, and Luis Izquierdo.
References
Bak, P. (1997). How Nature Works: The Science of Self Organized Criticality. Oxford, Oxford University Press.
Barthelemy, O. (forthcoming). Untangling Scenario Components with Agent Based Modelling: an Example of Social Simulations of Water Demand Forecasts. Centre for Policy Modelling. Manchester, UK, Manchester Metropolitan University. PhD.
Doran, J. (2005). Iruba: An Agent-Based Model of the Guerrilla War Process. Third Conference of the European Social Simulation Association, Koblenz, Germany., Verlag Ditemar Folbach.
Edmonds, B. (2001). The use of models - Making MABS more informative. Multi-Agent-Based Simulation. 1979: 15-32.
Edmonds, B. (2003). Towards an ideal social simulation language. Multi-Agent-Based Simulation Ii. 2581: 105-124.
Edmonds, B. (2005). Assessing the Safety of (Numerical) Representation in Social Simulation. 3rd International Conference of the European Social Simulation Association, Koblenz, Germany, Fölbach.
Edmonds, B. and J. J. Bryson (2004). The Insufficiency of Formal Design Methods " The Necessity of an Experimental Approach - for the Understanding and Control of Complex MAS. Proceedings of the Third International Joint Conference on Autonomous Agents and Multiagent Systems - Volume 2. New York, New York, IEEE Computer Society.
Edmonds, B. and S. Moss (2005). From KISS to KIDS - An 'anti-simplistic' modelling approach. Multi-Agent And Multi-Agent-Based Simulation. 3415: 130-144.
Engelfriet, J., C. M. Jonker, et al. (2002). "Compositional Verification of Multi-Agent Systems in Temporal Multi-Epistemic Logic." Journal of Logic, Language and Information 11(2): 195–225.
Fruhwirth, T. (1998). "Theory and practice of constraint handling rules." Journal of Logic Programming 37(1-3): 95-138.
Hales, D., J. Rouchier, et al. (2003). "Model-to-model analysis." Jasss-The Journal Of Artificial Societies And Social Simulation 6(4): U123-U129.
Hesse, M. B. (1963). Models and Analogies in Science. London, Sheed and Ward.
Ibrahim, Y. (2006). Automated abstraction of rule-based models of social and other multi-agent systems. Department of Computer Science. Colchester, University of Essex. PhD.
Ibrahim, Y. M. and P. Scott (2004). Abstraction for Rule-Based Multi-Agent Systems. Second Conference of the European Social Simulation Association, Valladolid, Spain.
Izquierdo, L. R., N. M. Gotts, et al. (2004). "Case-based reasoning, social dilemmas, and a new equilibrium concept." Jasss-The Journal Of Artificial Societies And Social Simulation 7(3).
Marriott, K. and P. J. Stuckey (1998). Programming with constraints: an introduction. Cambridge, Mass.; London, MIT Press.
Miller, J. H. (1998). "Active nonlinear tests (ANTs) of complex simulation models." Management Science 44(6): 820-30.
Moss, S., H. Gaylard, et al. (1998). "SDML: A Multi-Agent Language for Organizational Modelling." Comput. Math. Organ. Theory 4(1): 43-69.
Schrijvers, T. and B. Demoen (2004). The K.U.Leuven CHR system: implementation and application. First Workshop on Constraint Handling Rules, University of Ulm, Germany, Ulmer Informatik-Bericht.
Teran, O. (2001). Emergent Tendencies in Multi-Agent-based Simulations: using Constraint-based Methods to Effect Practical Proofs over Finite Subsets of Simulation Outcomes. Centre for Policy Modelling. Manchester, Manchester Metropolitan University. PhD: 296.
Teran, O. and B. Edmonds (2004). Constraint Model-based Exploration of Simulation Trajectories in a MABS Model, Centre for Policy Modelling, MMU.
Teran, O., B. Edmonds, et al. (2001). Mapping the envelope of social simulation trajectories. Multi-Agent-Based Simulation. 1979: 229-243.