Sociology and Simulation:
Statistical and Qualitative Cross-Validation
Abstract. The observance of unpredictable episodes of clustered volatility in some data series has led to the development of models of social processes that will give rise to such clustered volatility. Such models are not, however, validated directly against qualitative evidence about the behaviour of individuals and how they interact. An agent based simulation model of the effect of drought on domestic water consumption is reported here that is the outcome of a process of development involving stakeholders to inform and validate the model qualitatively at micro level while ensuring that numerical outputs from the model cohere with observed time series data. We argue that this cross-validation of agent based social simulation models is a significant advancement in the analysis of social process.
1.
The
issues.
The relationship between social processes and institutions and social statistics has been an important and controversial issue in sociology at least since the publication in 1904-5 of Max Weber’s The Protestant Ethic and the Spirit of Capitalism (Weber 1958). In this paper, we are concerned with that relationship. We argue that, on the basis of the evidence of social enquiry, analytic models do not obviously explain important properties of social statistics. However, a class of simulation models does generate numerical outputs that are consistent with important properties of real social statistics. These models have two further properties that should be of consuming interest to sociologists. One is that they appear to produce data with empirically relevant properties because they capture features of social order that are the subject of sociological enquiry – the social embeddedness of individuals together with the emergence of social norms. The other is that these models naturally draw upon and cohere with the sort of detailed, qualitative studies of social processes found in core strands of the sociological literature.
Our central argument can be seen as an operationalisation of some elements of structuration theory (Giddens 1984). According to Blaikie (1993), Giddens proposed that social research can take place at four related levels: (1) hermeneutic elucidation of frames of meaning, (2) investigation of context and form of practical consciousness, (3) identification of bounds of knowledgeability and (4) specification of institutional orders. Of these four levels, says Blaikie, the first two are “micro” and best investigated qualitatively while the second two are “macro” and best investigated with quantitative methods. This view is very close to ours. The micro behaviour is the behaviour of observed actors and described by autonomous software modules called agents. The macro behaviour is the behaviour of a social institution (organisation, community, set of customers, or whatever) or a collection of such institutions and is described by the properties of the model containing the agents. The properties of the model as a whole are amenable to summary using descriptive statistics while the behaviour of the individual agents can (and we argue should) be described qualitatively.
We neither seek nor claim an exact parallel with structuration theory. Agents are not replications of persons. They are simplified, formal representations. The simplicity and formality reduces the ambiguity of any analysis of their behaviour and social interaction at the cost of losing expressiveness relative to qualitative studies of observed actors. Consequently, there seems little to be gained by an in-depth study of a hermeneutic circle of a social simulation model. As will become evident below, there is more to be gained from an analysis of the social context of individual agents – the other agents with which they interact and the patterns and extent of the influence of specific agents upon one another. At the macro level, our concern is with the identification of ‘statistical signatures’ that can be explained by appeals to qualitative micro level behaviour and interaction. When such micro level phenomena can be demonstrated to describe aspects of observed social behaviour and interaction and, at the same time, to generate the macro level phenomena sharing the statistical signature of real social data, then we shall say that the model has been cross-validated. That is, the micro level behaviour has been validated qualitatively by domain experts and the macro level data has been validated by comparing statistical properties of the numerical outputs from the models with real social statistics. The link between the two is provided by simulations with the model. The chains of causation identified in simulation runs demonstrate a possible explanation of the link.
Our reliance on simulation models rather than closed analytic models together with our focus on empirical validation in relation to both qualitative and statistical data imply a methodology that relies on a close interaction between observation and conceptual development to the exclusion of prior theoretical specification. Our argument and methodology are atheoretical. We offer no view on the prospects for a general social theory but we do insist on the importance of observation-based conceptual development as a precursor to any future social theory.
We begin in section 2 with an account of a widespread social statistical signature that is shown in section 3 to be consistent with the sociological phenomenon of social embeddedness. In section 4, we give an example of cross-validation using a model of household water consumption incorporating agent designs based on descriptions of individual behaviour provided by domain experts from the UK water supply industry and regulatory agencies.
2.
Social
statistical signatures
Statistics are used by social scientists not only to inform descriptions of existing social phenomena but also to forecast future outcomes. In practice, there are many events that cannot be forecast. Indeed, there has never, in the history of statistical analysis, been a correct statistically based forecast of a turning point in either macroeconomic trade cycles or financial market prices and volumes.[1] Moreover, it has been known for more than a quarter-century, that statistical relations obtained from regression analyses on data covering one time period typically support different explanations of social relationships than are indicated by data covering a later (post-publication) time period (Mayer 1975).
In this section, we concentrate on a general feature of social statistics of which the unpredictability of turning points and changing statistical relations are a special case. and demonstrate that the problem is far more general than is normally recognised. Since most social science models with this purpose are economic in nature and predictive in (avowed) purpose, we will start by examining their success. Since they are predictive rather than explanatory in purpose, it is on predictive success they are judged. Our purpose is more fundamental, namely to examine the usefulness of such kinds of model to capture social phenomena and the statistics derived from them.
Both forecasting failure and unpredictable changes in estimated statistical relationships can be consequences of clusters of volatility in the data where neither the timing nor the magnitude nor the duration of the volatility can be predicted. Some obvious cases are turning points in macroeconomic time series associated with upturns and downturns in economic performance (investment, employment, consumption, etc.) and turning points in stock market prices. These turning points are marked by much bigger changes in the values of statistical variables than are observed between turning points – indeed, such marked turning points are instances of clustered volatility.
The usual explanations of unpredictable macroeconomic turning points are either some kind of structural change (Clements and Hendry 1995; Clements and Hendry 1996) or that volatility begets volatility (for a while) (Bollerslev 1986; Engle 1982; Hansen 1982) so that the parameters of the statistical distribution from which observations are said to be drawn themselves vary over time. The latter set of techniques constitute the approach of time varying parameters (TVP). None of the estimating approaches associated with either of these explanations has yielded a correct forecast of a turning point or any other episode of volatility. The TVP approach has also been applied to financial data with no more success than to macroeconomic data (Bollerslev 2001).
The only tests of the goodness of these techniques is their ability to capture salient aspects of the data series to which they are applied. Like all other forecasting techniques, they fail to forecast future clusters of volatility. The TVP approach does capture some aspects of previously observed data series but only because those aspects are already implicit in the estimating techniques (Tay and Wallis 2000).
The wide recognition of the recalcitrance of macroeconomic and financial market turning points to forecasting has not been extended to the time series data from other social and economic processes. Yet, the more general observation of unpredictable clusters of volatility appears to be far more widespread. As Moss (2002) has pointed out in a slightly different context, unpredictably clustered volatility characterises the sales values and volumes of many fast moving consumer goods sold in UK and US supermarkets and, we now demonstrate, to domestic water consumption.
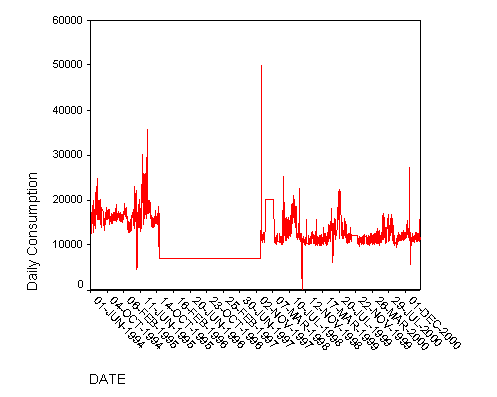
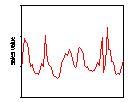
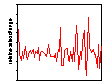
Figure 1: Daily water consumption (litres per day) in a metered UK neighbourhood
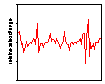
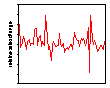
It is clear from Figure 1 that there are occasional spikes, both upwards and downwards, in domestic water consumption that might be associated with weather conditions but that do not occur at the same times of the year. While the quality of the data in general as good as we can expect, there is a long period from October, 1995 into November 1997 when the readings were constant. This is clearly a problem with the data collection and the data for that period has been excluded from all subsequent analysis. Figure 2 shows the graph of proportional changes in the daily consumption of water.
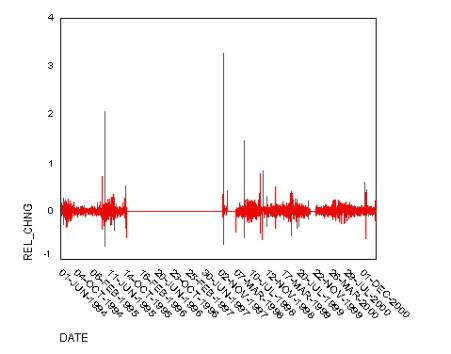
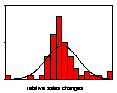
Figure 2. Relative changes in daily water consumption
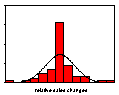
The histogram in Figure 3 gives
the frequency distribution of the changes in the daily values of water
consumption and the continuous ogive is the normal distribution for the same
mean, standard deviation and sample size.
The standard test for normality is the Kolmogorov-Smirnov statistic
which gives, to three significant figures, zero confidence that the observed
distribution is normal. The higher,
thinner peak of the actual frequency distribution with respect to the
corresponding normal distribution is called leptokurtosis (=
thin-peaked) and is due to the presence of significant numbers of values
relatively far from the mean. These
distant values are manifestations of volatile episodes.
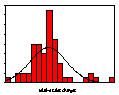
Similar results are found in sales value and volume data for a wide range of fast moving consumer goods. An example, reproduced from Moss (2002), is UK supermarket sales data for three brands of shampoo. Similar results are found for virtually every one of the 120 or so brands of shampoo for which we have the data as well as every brand of tea, shaving preparations, biscuits and, in the US as well as the UK, every one of some 200 brands of spirituous alcoholic beverage and beers. The first row of Figure 4 shows weekly sales values. Brand A is a leading brand with no discernable sales trend while sales values of brand B are declining and sales values of brand C are increasing. Both of the latter have small market shares. The second row shows the time series of relative sales changes. Over the 65 weeks there were obvious clusters of volatility and it is these clusters that generated the extreme values that cause the leptokurtosis evident in the third row showing the frequency histograms of the relative sales changes compared with the corresponding normal distribution.
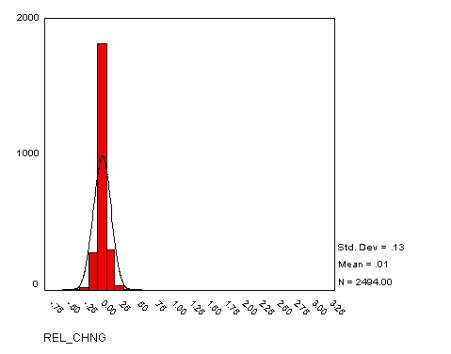
Figure 3: Frequency histogram and normal ogive for relative changes in daily water consumption data
Each data set manifesting leptokurtosis and clustered, large changes in variable values can be ascribed a separate and special reason. In markets for fast moving consumer goods, the phenomenon might be due to special offers (though we have found no evidence that this is so). In water consumption data, the clustered changes could be due to the weather (though seasonally adjusting the data does not affect the outcome). In the financial markets, there are speculative bursts (though it seems to us implausible that widespread shifts in expectations might be the result of strictly individual sentiment). In national and international economic systems (or macroeconomies) episodes of large clustered changes are often put down to some kind of structural break or exogenous force (though if these were uniquely identifiable the occasions on which their consequences amounted to a turning point in the trade cycle ought also to be uniquely identifiable and hence correctly forecast). Rather than to look only for special reasons to account for unpredictable and clustered volatility in each type of social institution, we find it natural to investigate whether there is any element of generality in the generation of these unpredictable phenomena.
|
Shampoo
A |
Shampoo
B |
Shampoo
C |
|
|
|
|
|
|
|
|
|
|
|
|
Figure 4: Weekly shampoo sales and relative sales change; 2 Jan 2000-25 March 2001 (Source: Information Resources International; reproduced from (Moss 2002))
3.
Volatility
and social embeddedness
Following Granovetter (1985) and Edmonds (1999a), we define social embeddedness as a state in which an actor is significantly influenced by individual relationships with other actors. That is, the influences on the actor can not be modelled as if all actors were identical (by using, for example, representative or homogeneous agents). The particularities of its interactions with those to which it relates have a significant impact upon the outcomes in the model. While social embeddedness neither implies nor denies optimising behaviour of the sort assumed by economists, it does mean that the simplifying assumptions used by economists in their formal analytic models critically distort the phenomena being analysed.
There appear to be no models incorporating agents as defined in conventional economic theory that generate the unpredictable volatile clusters described in the preceding section. Indeed, results from a wide range of agent based social simulation models suggests that four conditions are associated with clustered volatility at the macro level. The four conditions are:[2]
· Individuals are metastable in the sense that they do not change their behaviour until some level of stimulus has been reached. They would not, for example, reconfigure their desired shopping basket as a result of a penny rise in the price of a tin of tuna or change their religion because they dislike a sermon. A particular implication of metastability is that the behaviour of individuals cannot be represented by utility maximising agents.
· Interaction among agents is a dominant feature of the model dynamics. This amounts to social embeddedness in the sense of Granovetter (1985): the behaviour of individuals cannot be explained except in terms of their individual interactions with other individuals known to them.
· Agents influence but do not slavishly imitate each other.
· The system is slowly driven so that most agents are below their threshold (or critical) states a lot of the time. In effect, most of us engage in routine behaviour most of the time without fundamentally changing either our behaviour or the expectations that drive that behaviour. The system is slowly driven if we are not frequently being overwhelmed by pressures to change expectations and behaviour.
An agent based social simulation model contains agents that are independent computer programs with an ability to perceive aspects of their environments (including some other agents) and to process those perceptions in order to produce some effect on their environment (including other agents) and perhaps to change the ways in which they process perceptions into actions. As will be explained in more detail below, an important feature of agents is that they and their interactions can be designed by the modeller to describe the behaviour and interactions of social entities, whether individuals or organisational units. Consequently, agent based social simulation models can be validated by comparing the agents and their social behaviour with individual and social behaviour found in real societies and by comparing the properties of numerical outputs of these models with the properties of real social statistics.
Unfortunately the meanings of such phrases as “statistical signature” and “the properties of real social statistics” are by no means clear and unproblematic. In some cases, the variance or even the mean of a distribution is not defined. There is even no reason to believe that observed social statistics are drawn from some fixed, underlying population distribution and some reason to believe that (in some cases) they are not. These issues will be investigated in section 5. In the meantime, we note that both societies and models can be viewed as data generating processes. Many social arrangements including national economies, retail shops and supermarkets and collections of households generate time series data marked by clusters of volatility the timing, magnitude and duration of which cannot in practice be forecast. Models with by the above four characteristics also generate time series data with the same clustered volatility properties.
In the following section, we describe a model and the background to its development in order to exhibit the extent to, and ways in which, that model is validated by domain experts. We also report simulated time series data generated by the model under various assumptions in order to suggest that the simulated data, like the real data, exhibit unpredictable clusters of volatility. We also note the incompleteness of the validation as well as problems with the identification of the statistical signatures of leptokurtosis due to clustered volatility.
4.
A
model of social influence on domestic water consumption
The model reported in this section has been developed through five distinct versions. The first version was constructed with little input of domain expertise in order to capture the effect of enjoinders on households to conserve water during periods of drought. This version demonstrated that social influence was sufficient significantly to reduce domestic water consumption when a minority of households were easily influenced by official requests provided that some households were so influenced and other households were influenced by other households with whom they had some stable relationship and were, in a well defined sense, similar to themselves. Domain experts from the water supply companies evaluated the first version which they found deficient in that, when a drought ended, aggregate water consumption immediately returned to its pre-drought levels. The second version was designed to address this deficiency. Whereas, in the first version, households would observe and be influenced by the actions of their neighbours in the prevailing conditions, in the second version it was only the neighbours’ actions that influenced households and, moreover, the influence as assumed to decay over time in accordance with evidence from experimental cognitive science (Anderson 1993).[3]
The third version of the model introduced the effect of new technology on domestic water consumption. Because of Victorian public health legislation in the United Kingdom, it was not until recently permitted to apply mains pressure to domestic hot water. As a result, “power showers” were introduced in the early 1990s which involved the pumping of shower water under substantially higher pressure than could previously be obtained. This was clearly a high-water-use technology, the adoption of which would increase domestic water consumption. The first model version to incorporate technical change resulted in the complete adoption of power showers within a few months of their introduction. In fact, the penetration of power showers among households in the regions for which we have data has not, after more than a decade, reached 45%. While adoption was driven by the same sort of social influence that drove the responses to enjoinders to conserve water during periods of drought, there were no impediments to adoption by households. Informants from the UK Environment Agency, the regulator responsible for water quality and supply sufficiency, suggested that in practice power showers are installed as part of a more general bathroom renovation and households do not normally renew bathrooms more frequently than once in five years. Other appliances such as dish washers and washing machines are replaced either as part of a wider renovation or when they break down. The representation in the model of such restraints on replacement and therefore innovation has served to replicate the broad time pattern of changes in ownership patterns.[4]
We do not claim that the representation of household behaviour by agents is accurate. Only that it reflects the views of domain experts from the water supply companies and the relevant regulating agency. Further validation could be obtained by means of standard survey and interview techniques. These would enable us to elaborate the agents as representations of households and perhaps to calibrate the model, especially in relation to the susceptibility of households to influence either from government and water companies or from their social networks.
The model was not designed to illustrate the effects of social embedding in agent-based social simulations but was incrementally developed to reflect expert and stakeholder opinion on the influences on households with respect to their habits concerning the use of water-consuming appliances, and hence, indirectly, how much water they consume. Only later did we discover that it also demonstrated the role social embedding plays in creating the sort of fat-tailed time series with clustered volatility that we have been discussing. However, this was not surprising since our experience leads us to expect this result from models of this kind.
The water consumption model focuses upon the behaviour of households, in particular how the household-to-household behavioural influence affects the aggregate demand for water. Thus the heart of the model is a network of agents each of which represents a single household. These are distributed randomly on a two dimensional grid. These ‘households’ can only interact with those with a certain distance of them, vertically and horizontally – their ‘neighbours’. The totality of households and their potential interactions can be considered to represent a community or cluster.
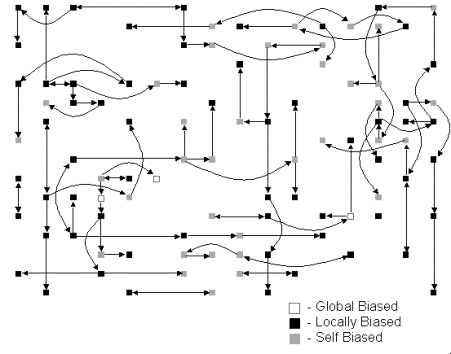
Figure 5. Influence network of between ‘most-similar’ households at a typical instant of simulation time
We know from a half-century or more of social psychological studies (refs) that individuals tend to form stable social relationships with persons with whom they already have common social backgrounds and interests and, once such relationships are formed, the opinions and behaviour of these individuals tend to be similar. In order to capture this finding, agents are designed endorse as most similar to themselves those neighbours whose water consumption behaviour is most like their own. Such neighbours are then of particular importance in terms of influence. The network of all the possible avenues of influence by such endorsed neighbours is shown in Figure 5. The total web of possible influences among households is not shown as it is too dense to be sensibly displayed. This structure was chosen to be consistent with what domain experts told us about influence between households. The result is that agents are given a non-uniform local network of relationships within which each household determines neighbours by which they are most influenced.
The external environment for each household consists of: the temperature and precipitation; the exhortations of the policy agent (which used to be a government agency and is now the local water company); and, critically, the neighbouring households. Each household has a number of different water-using devices such as: showers, washing machines, hoses etc. The distribution and properties of these devices among agents matches the distribution of these appliances among households as obtained in a recent survey. The numerical outputs include the volume of water the used by each household in each appliance from which we calculate total domestic water consumption and the time patterns of the effects of new technologies on water consumption.
The domestic water consumption model captures hydrological phenomena as well as processes of social influence that are believed to affect the domestic demand for water. The hydrological element determined the addition to the water supply each month given actual temperature and precipitation as well as the month (hence hours of daylight influencing water transpiration (from plants and animals) and evaporation into the atmosphere. Since our temperature and precipitation data was monthly, the month was the level of time step used to calculate consumption.
Each month, each household adjusts its water-using habits, in terms of the amount it uses each device, and whether it acquires new devices (such as power showers). It does this adjustment based on the following: what devices it has; its existing habits; what its neighbours do (except for private devices such as toilets); and what the water company may be suggesting (in times of drought). The weighting that each household uses for each of these is different and is set by the modeller. In many of the runs it was set such that about 55% of the households were biased towards imitating a neighbour; 15% were predisposed to listen to the water company and the rest were largely immune to outside suggestion. Obviously it is not known what proportions might be more realistic in terms of real communities, but anecdotal accounts suggest it varies greatly between communities.
The “policy agent” represents the body responsible for issuing guidance to consumers as to water use in times of water shortage (currently this is the individual water companies in each area). In the model there is a calculation of the level of ground water derived from the climatological data, and the policy agent starts issuing suggestions during the second month where the ground is dry. In subsequent dry months its suggestions are to use increasingly less water.
The model structure is illustrated in Figure 6.
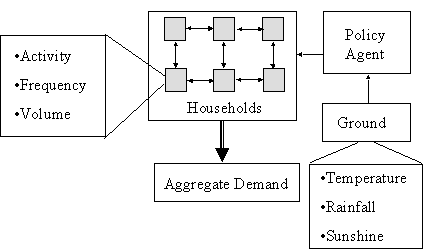
Figure 6. The structure of the model of domestic water demand
The model does not attempt to capture all the influences upon water consumption. In particular it does not include any direct influence of the weather upon micro-component usage nor does it include any inherent biases towards increased usage due to background social norms such as increased cleanliness. The behaviour of the policy agent is not sophisticated since it is the reaction of the households that is important here.
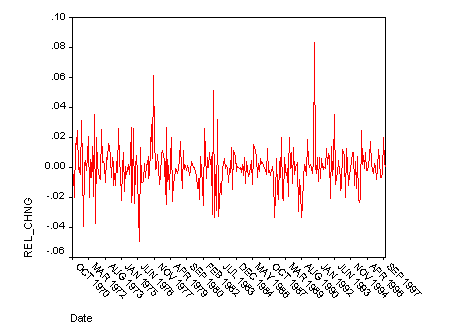
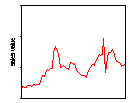
Figure 7. Simulated relative change in monthly consumption

Figure 8. Relative changes in simulated monthly water consumption
The times series from an typical run is shown in Figure 7. It exhibits clustered volatility similar to that seen in the water data usage shown above (Figure 2). The histogram of the relative changes is shown in Figure 8 – this shows the same level of leptokurtosis as was seen in the corresponding histogram for the water usage shown above (Figure 3).
Equally importantly, the model exhibited a variety of responses to the same external conditions. Figure 9 shows the aggregate usage from the model for 12 different runs of the same model subject to the same climate data and external interventions (principally the droughts in 1976, 1990 and 1996, the introduction of power showers in 1990 and new water-saving washing machines in late 1992).[5]
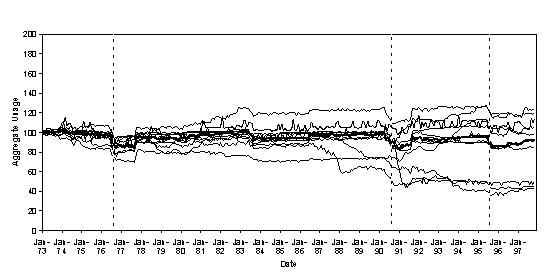
Figure 9. 12 runs of the water demand model under the same conditions (bold line is median demand)
To investigate the importance of the embedding of the agents in the model, we ran the model again with exactly the same structure, parameters and inputs, but with the neighbourhood relations randomised. That is, where in the previous versions of the model a household might be influenced by its neighbours as to its patterns of water usage, in this version the neighbour ‘sees’ a different random selection of neighbours each time. Thus patterns of influence are randomised and different at each time period in the simulation. The corresponding patterns of aggregate water usage that are produced by the model are shown in Figure 10.
In the version where the social embedding is disrupted we notice two ways in which the aggregate behaviour is different to the original version. Firstly, there is a greater level of local oscillation in the demand. Secondly, there is almost no systematic, collective response to the occurrence of droughts, as is indicated by the course of the median of the demand lines. The consequences of the removal of social embedding from the model is that we no longer capture events that were of considerable importance to stakeholders. That is, prior to the privatisation of the water supply industry in the United Kingdom, exhortation and to save water restrictions on water use during droughts were effective to the point of neighbours reporting others who were, despite hosepipe and sprinkler bans, watering their gardens. After privatisation, there was public concern about the very large increases in senior managerial remuneration packages and outrage at the discovery that more than half the water in the mains was lost through leakage while households were being exhorted to conserve water. As a consequence, there was very little reduction in household water consumption post-privatisation. Our models with and without social embeddedness support the conjecture that social responses are conditioned by social embeddedness.
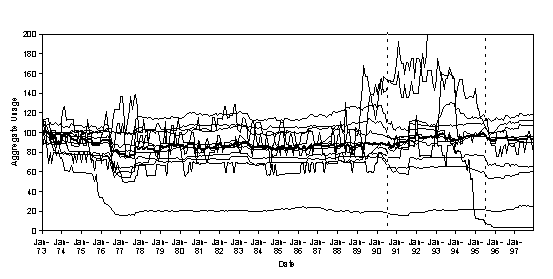
Figure 10. 12 runs of the water demand model under the same conditions where the social embedding is disrupted (bold line is median demand)
5.
Descriptive
Statistics vs. Statistical Models
The presumption that statistics is ‘science’ but qualitative research is ‘mere anecdote’ is at variance with our experience of participatory agent based modelling.
Our agent-based models often produce time series data that are characterised by clustered volatility and high levels of leptokurtosis. This is not because we tune our models to produce these kinds of time series but seems to be a consequence of the characteristics we put in to our models, namely: social embeddedness; the prevalence of social norms; and individual behaviour. The reason we often make models with these characteristics is that these are a necessary part of making our models consistent with the observations of sociologists and other domain experts concerning the behaviour of the actors concerned. The fact that the time series derived from social phenomena often have these same characteristics may indicate that the models are on the right track.
This is in sharp contrast to many statistical approaches, where it is assumed that conventional statistical models and tools will apply. These assumptions are often completely unwarranted and seem to be made purely because due to a perceived lack of choice. The burden of proof should be on those who wish to make these assumptions, otherwise they will be merely ‘muddying’ the debate with statistical artefacts by presenting ‘results’ that do not fundamentally derive from the social phenomena we are concerned. It is not possible to prove that such assumptions are wrong – it is always logically possible that there is an well-defined, fixed distribution function underlying the time series, even when all the indications of available data are to the contrary. One can always assume that such a distribution can be recovered by means such as: increasing the sample size; considering a longer series; and excluding ‘exceptional’ events.
The time series that results from social phenomena and the agent-based models of these phenomena provide some evidence against these sort of assumptions. Agent-based models that seek to be consistent with the anecdotal evidence of how social actors behave often produce time series which are best described by power laws, Pareto distributions and the like. The extreme ‘peaks’ observable in the time series they produce do not always result from substantial or exceptional factors but are intrinsic products of the processes captured by the models. This adds credibility to the hypothesis that similar processes could be responsible for the similar time series derived from social phenomena.
If one insists on assuming the
time series obtained from social phenomena can not only be described by
fixed distributions in a post-hoc manner but are also generated by them (in some underlying or a priori way), then the high levels of leptokurtosis and clustered volatility
do not support an assumption that such distributions as the normal, binomial
are applicable, but rather fit those like the Pareto distribution. With the Pareto distribution high levels of
leptokurtosis indicate that the second moment (the variance) is undefined – in
other words, that you as you take longer samples the variance will not tend to
a limiting, ‘stable’ value. In fact,
over half of its parameter space, the Pareto distribution do not even have a
defined mean.
If we were to suppose that a particular social process generates data described by a Pareto distribution function, then the prevalence of leptokurtosis implies that, in general, that distribution function has no defined variance and very likely has no defined mean. That is, increasing the number of observations will not result in the convergence of an undefined mean or variance to any fixed population value.
Considered as a data generating process, social institutions in this case would not produce numerical data that can be treated as if they were drawn from an underlying population distribution. We would not expect social environments marked by clustered and unpredictable volatility to generate data described by a fixed frequency distribution. This is because social institutions frequently respond to episodes of volatility by changing the behaviour of the institution. A clear example is the changes in the norms and rules governing trading in organised financial markets. These rules are typically changed after a serious downturn as happened after the financial panics of the 19th century (after which stocks were issued fully paid up), certainly after the 1929 crash (when the value of debt that stockbrokers could lend customers against their portfolio values were limited by law in the United States) and, more recently, after the 1987 downturn in world stock markets (when trading pauses were introduced in conditions where automated trading appeared to have become unstable). Other example include corporate reorganisations, consequences of technical change and changes in political regimes (e.g., the French Revolution or the ‘revolutions’ in Eastern Europe in 1989).
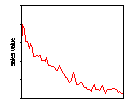
That there is no evidence that the variance of daily domestic water consumption is settling down to a defined variance can be seen in Figure 11.[6] This figure is similar to the (lack of) convergence found by Mandelbrot (1963) in financial time series.
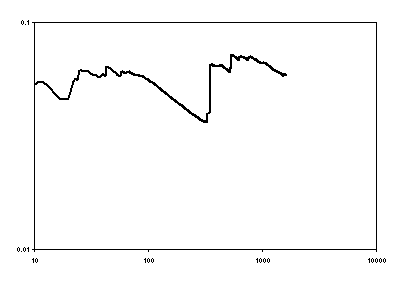
Figure 11: The cumulative variance of log changes in daily domestic water consumption (litres per day) in a metered UK neighbourhood (derived from the figures illustrated in figure 1 above).
It is likely that much of the apparent normality of some socially derived time series is an artefact of the way they are produced. A consequence of the central limit theorem is that any averaging in the construction of the data (either implicit as in summing over fixed time periods or explicit) will tend to make the data appear more normal. For example if daily time series has a high descriptive leptokurtosis then the monthly series will have a much lower level of leptokurtosis. To illustrate this we took the water consumption data illustrated above in Figure 2 and averaged it in consecutive groups (e.g. the first four numbers, the second four etc.) and then constructed frequency distributions of the resulting figures. Three of these distributions are illustrated in Figure 12. The distribution becomes clearly less leptokurtic as the grouping size increases. The Kurtosis for different levels of averaging is shown in Table 1.
|
Group size |
1 |
2 |
4 |
8 |
16 |
32 |
|
Kurtosis |
2490.0 |
130.1 |
82.5 |
39.5 |
33.5 |
15.7 |
Table 1. Kurtosis of the frequency distribution of relative changes of water consumption after being binned into different size groups
|
Group size 2 |
Group size 8 |
Group size 32 |
|
|
|
|
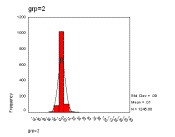
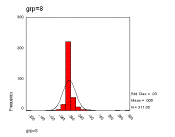
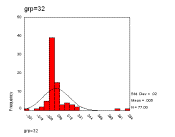
Figure 12. The frequency distributions of the relative changes, grouped in sizes 2, 8 and 32 respectively
This result serves to illustrate the difference between descriptive statistics and statistical models of the underlying process. The former is a numerical description of some data whilst the later is a model of the data-generating process – conflating the two can be misleading.
The lack of an underlying fixed distribution behind the phenomena indicates a capacity endogenously to generate dynamic and/or structural change. This change results, in part, from the ability of a system to ‘re-wire’ itself into new configurations. It seems plausible that this ability is limited by the complexity of the system. Although agent-based models are considerably more complex that analytic models they are still formal systems and, hence, much simpler than the social processes they seek to capture. The simplistic nature of the influence mechanisms in the water demand model and its limited size (40 or 100 agents, depending on the purpose of the experiment) are probably not sufficient to bring about such structural changes endogenously. Indeed this is indicated by the fact that, unlike the real water demand statistics, the variances of the demands from the model do seem to be defined. The equivalent of Figure 11 for the demand time series derived from the embedded model is shown in Figure 13.

Figure 13. The cumulative variance of changes in the log values of the water demand time series derived from 12 runs of the model.
It seems essential to us that in good (social) science, observation of how processes actually occur should take precedence over assumptions about the aggregate nature of the time series that they produce. That is, generalisation and abstraction are only warranted by an ability to capture the evidence. Simply conflating descriptive statistics with a (statistical) model of the underlying processes does not render the result more scientific but simply more quantitative.
In the end this comes down to deep assumptions about the nature of the phenomena one is concerned with, especially about the characteristics of what might be considered as ‘noise’. In any model one will only be able to capture limited certain aspects of what one is modelling – the rest can be thought of as ‘noise’. However one can not assume that this noise is random (in a statistical sense), just because it is unpredictable. One can not even assume that this noise will obey the ‘Law of Large Numbers’ – which, broadly stated, is the property that random noise will cancel out faster than any ‘signal’ as sample size increases. Models that illustrate this possibility include Kaneko’s example of ‘Globally coupled chaos’ and Brian Arthur’s ‘El Farol Bar’ model (Arthur 1994) as investigated in (Edmonds 1999b). What we do not understand about social phenomena, even through the lens of aggregate time series, can not be dealt with as simply as an engineer might treat meaningless electrical fluctuations.
6. Conclusion
The water consumption model presented in this paper represents an attempt to describe a social process that is consistent with both the qualitative data provided by stakeholders and other domain experts and observed characteristics of time series data concerning domestic water consumption. Each successive version of the model has been subject to validation by domain experts. Their validation concerned both the representation of agent behaviour and interaction as well as characteristics of the aggregate time series output (especially the recovery of demand after drought-induced restrictions have been rescinded).
This approach differs fundamentally from the usual approaches to statistical research. and extends the usual approaches to qualitative research. Both of these features of our approach depend crucially on the use of agent based social simulation models.
Although agent based modelling is in widespread use, the agents are not universally implemented as descriptions of the behaviour of observed social entities. It is not uncommon, for example, for agents to be specified as genetic algorithms (Chen and Yeh 2002; LeBaron, Arthur and Palmer 1999; Palmer et al. 1993) or as artificial neural networks (LeBaron 2002) or as players in a game theoretic setting (Macy and Sato 2002)[7]. While these agent designs are sometimes implemented in simulation models addressing issues of concern to sociologists such as trust or social norms, the agents themselves cannot be compared directly with the behaviour of the individuals or composite social entities they are intended to represent. Such designs do not facilitate validation of the agents using qualitative data and qualitative research methods. Particularly in the case of models of financial markets, such agent based models do generate leptokurtic time series data due to clustered volatility. Typically, these models satisfy the four conditions of agent metastability, interaction, social influence and being slowly driven. We do not know whether all such models will generate leptokurtosis and volatility[8] but we do know that commonly they do.
What these models show is that the observed features of aggregate time series data for financial markets, macro economies and markets for fast-moving consumer goods can be the result of data generating processes in which there is no individual maximising behaviour and in which interaction among individuals is crucial. However the TVP models discussed in section 2 also produce aggregate time series data with the same observed properties. And these models are intended to be consistent with the economic rational expectations hypothesis based on the presumption that individual do maximise utility and that they are not socially embedded. Although the TVP models, unlike the agent based models, have no formally elaborated micro element, they are neither more nor less well validated than the agent based models implementing agents as genetic algorithms, artificial neural networks or game theoretic strategies.
We have shown that descriptive statistics are insufficient to identify the processes that generated the data. We have also shown that, provided the data is sufficiently fine grained, some models of data generating processes can be shown to be consistent with that data and some can be excluded. But to choose among the classes of models that purport to describe the underlying data generating process must require some additional discriminants. To avoid mere tautology, such discriminants must be empirically based. Additional statistical data is of no help since we have already shown that such data cannot be used to discriminate among the possible data generating processes. If we are not to use statistical data for this purpose, we must use qualitative data or at least data describing micro behaviour. In designing and developing our domestic water consumption model, we used qualitative data and assessments provided by domain experts and, in particular, by stakeholders in the water resource management process. As a result, the models were assessed independently in relation to the macro level statistical data and the micro level qualitative data – the process we have called cross-validation.
We believe it to be both interesting and important that the process of validating the model qualitatively at the micro level is clear and straightforward while the validation using macro level statistics is suggestive and based on visual impressions of clustered volatility. This experience stands on its head the notion that qualitative research is mere anecdote while statistics is science.
Our aim has been to demonstrate that agent based models have the particular strength that they can be validated with respect to both qualitative and statistical data and at both micro and macro levels. In so doing, we have identified a number of further issues that need to be addressed.
We have reported that some of our models generating leptokurtosis and clustered volatility do and some do not produce time series data with apparently convergent moments of the frequency distributions of those data. The differences in the models that lead to these different results might well be important but we have no idea of what it is that causes those differences. In particular, we do not know whether these differences are artefacts of the model or something the model represents about social relations and individual behaviour. We simply point out that if the distributions are stable, then a non-convergent variance is consistent with a Levy distribution and a convergent variance is not. This result will be important to those who investigate empirical distributions of personal incomes, firms sizes, market shares, city sizes or any of the other power law distributed cross sectional and time series economic data since power law distributions are a consequence of the Levy distribution.
A second problem is that the notion of the “statistical signature” is without formal content. If we are to use the features of social statistical data to identify classes of possible models of social data generating processes, then it would clearly be useful if we could relate formal descriptors of the data to features of suitable data generating processes.
We have also pointed out that the common practice in social simulation of producing a series of runs and then reporting summary statistics such as median values can hide important episodes of volatility. Yet, the reasons for running suites of simulation experiments – to identify robust properties of the models – is surely valid. There is a tension here that needs to be addressed.
Finally, we do not claim to be experts in qualitative research. We are, however, aware that some social researchers are uncomfortable about generalising from the experiences of individual organisations and institutions. We do not speculate as to whether there is any justice in this position but we do claim that more formal representations of qualitative evidence by agent based social simulation models provides a means of identifying any general properties of social systems that are consistent with independently observed macro level data.
References
Anderson, J.R. 1993. Rules of the Mind. Hillsdale NJ: Lawrence Erlbaum Associates.
Arthur, Brian. 1994. "Inductive Reasoning and Bounded Rationality." American Economic Association Papers 84:406-411.
Blaikie, Norman. 1993. Approaches to Social Enquiry. Cambridge: Polity Press.
Bollerslev, T. 1986. "Generalized Autoregressive Conditional Heteroskedasticity." Journal of Econometrics 31:307-327.
—. 2001. "Financial Econometrics: Past Developments and Future Challenges." Journal of Econometrics 100:41-51.
Chen, S.H., and C.H. Yeh. 2002. "On the emergent properties of artificial stock markets: the efficient market hypothesis and the rational expectations hypothesis." Journal of Economic Behaviour and Organization 49:217-239.
Clements, M.P., and D.F. Hendry. 1995. "Macro-economic Forecasting and Modelling." Economic Journal 105:1001-1013.
—. 1996. "Intercept Corrections and Structural Change." Journal of Applied Econometrics 11:475-494.
Downing, Thomas E., Scott Moss, and Claudia Pahl Wostl. 2000. "Understanding Climate Policy Using Participatory Agent Based Social Simulation." Pp. 198-213 in Multi Agent Based Social Simulation, edited by Scott Moss and Paul Davidsson. Berlin: Springer Verlag.
Edmonds, B. 1999a. "Capturing Social Embeddedness: a Constructivist Approach." Adaptive Behaviour 7:323-348.
—. 1999b. "Modelling Bounded Rationality In Agent-Based Simulations using the Evolution of Mental Models." Pp. 305-332 in Computational Techniques for Modelling Learning in Economics, edited by T. Brenner: Kluwer.
Engle, R.F. 1982. "Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation." Econometrica 50:987-1007.
Giddens, Anthony. 1984. The Constitution of Society. Cambridge: Polity Press.
Granovetter, M. 1985. "Economic-Action and Social-Structure - The Problem of Embeddedness." American Journal Of Sociology 91:481-510.
Hansen, L.P. 1982. "Large Sample Properties of Generalized Method of Moments Estimators." Econometrica 50:1029-1054.
Jensen, H. 1998. Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems. Cambridge: Cambridge University Press.
LeBaron, B. 2002. "Short Memory Traders and their Impact on Group Learning in Financial Markets." Proceedings of the US National Academy of Sciences 99:7201-7206.
LeBaron, B., W. B. Arthur, and R. Palmer. 1999. "Time series properties of an artificial stock market." Journal of Economic Dynamics & Control 23:1487-1516.
Macy, Michael W. 1991. "Learning to Cooperate: Stochastic and Tacit Collusion in Social Exchange." American Journal Of Sociology 97:808-843.
Macy, Michael W., and Yoshimichi Sato. 2002. "Trust, cooperation, and market formation in the U.S. and Japan." Proceedings of the US National Academy of Sciences 99:7214-7220.
Mandelbrot, B. 1963. "The Variation of Certain Speculative Prices." Journal of Business 36:394-419.
Mayer, Thomas. 1975. "Selecting Economic Hypotheses by Goodness of Fit." The Economic Journal 85:877-883.
Moss, Scott. 2002. "Policy Analysis from First Principles." Proceedings of the US National Academy of Sciences 99:7267-7274.
Palmer, R., W. B. Arthur, J.H. Holland, B. LeBaron, and P. Taylor. 1993. "Artificial Economic Life: A Simple Model for a Stock Market." Physica D 75:264-274.
Tay, Anthony S., and Kenneth F. Wallis. 2000. "Density Forecasting: A Survey." Journal of Forecasting 19:235-254.
Weber, Max. 1958. The Protestant Ethic and the Spirit of Capitalism. New York: Scribners.