The Power Law and Critical Density
in Large Multi Agent Systems
Centre for Policy Modelling,
Manchester Metropolitan University
, Manchester M1 3GH, UK
{s.moss b.edmonds s.wallis}@mmu.ac.uk
Abstract. Agents that act as information brokers in large distributed systems (such as the internet) lower the cost of obtaining information. Agents have direct access to only a small part of such systems at any one time. This paper investigates the conditions in which agents successfully go through other agents in order to establish direct communication. A sumulated, large information market enables agents to acquire the information they seek if and only if market shares amoung broker agents conform to a power law distribution. This result, if it turns out to apply more generally, implies that agency theory based on utility maximisation does not provide any guidance to system properties. Thus certain aspects of the agent decision making process are implied by the properties of the system.
1 System structures
The issue addressed in this paper is the relationship between properties of multi agent systems and agent design. The particular classaspect of large MAS considered here are large in the sense that no agent can directly encounter or observe all other agents.
It has long been observed that large natural and social systems are frequently characterised by the power law distribution. Vilfredo Pareto [12] first observed that the distribution of income among households is a power law distribution. Industrial economists have long recognised that firm sizes also follow the power law distribution, a property that Axtell [3] has recently found to emerge from simulations of the emergence of trading agents representing firms. What brings the power law closer to the interests of agent theory is the finding by Adamic and Huberman [1] that the distribution of visits to World Wide Web sites is also a power law distribution.
It appears that real, large systems with many autonomous but interacting components are characterised by power law distributions. Any investigation of the properties of large software systems, whether by means of simulations or formal analysis, will therefore be more convincing if the systems are shown to exhibit appropriate power law distributions. The power law distribution is, in effect, an observed statistical signature of large systems of autonomous, interacting entities such as software agents. For purposes of software engineering, the point is not to replicate either real social systems or software systems such as the World Wide Web, but rather to design mechanisms and agent architectures that successfully meet user requirements.
It will be demonstrated here that, for a simulated large multi agent system, user requirements for information exchange can be met only if there is some critical density of agents in the system and this critical density is also the density at which the distribution of activity among agents is a power law distribution. This result suggests that the power law distribution is an indicator of the ability of large multi agent systems to meet user requirements.
2 Agent architectures and statistical signatures
The power law states that, ordering objects according to the share of values or events ascribed to each object, then starting with the object with the smallest share of values or events, the cumulative value or number of events is related to the cumulative number of objects by the power function
|
|
(1) |
or, equivalently,
|
|
(2) |
In either form, the implication is that a small number of objects are associated with very large shares of the relevant values or events and a large number of objects with very small shares. The power law distribution implies characteristics of a system with statistical measures. The values of these measures represent statistical signatures of the system. This notion of the statistical signature is an analogy with the statistical signature of wave theory as the parameters of the Fourier transform of the wave form.
One virtue of the power law as a statistical signature for multi agent systems is that it can be used to identify agent architectures that are inappropriate for the system. The example developed here relates to software agents populating virtual markets. If the distribution of market shares over supplier agents obeys the power law, then a small number of supplier agents will have large market shares.
This is an important issue for agent and mechanism design if those designs rely on conventional economic concepts and, in particular, utility maximising agents. This is because one consequence of the power law distribution is that some suppliers might offer such a large proportion of total supplies that their offers influence the prices they receive. In such cases, if all customer agents are expected utility maximisers and all supplier agents are expected profit maximisers, then the ratios of prices to marginal utilities are the same for all goods and all agents. These are conditions for an economic system to be in equilibrium will not be satisfied.
The problem here is that Lipsey and Lancaster [7] proved that if any of these conditions are not satisfied because, for example, one or more suppliers can influence prices, then nothing can be said in general about the efficiency of the whole system or how to change the efficiency of the system. Consequently, in such circumstances the specification of agents as expected utility and/or profit maximisers provides no information about the properties of the multi agent.
In a companion paper, Moss [10] demonstrated that, in a simulation of a small closed system, the specification of agents as profit and utility maximisers restricted the scale and properties of the system and that dropping the maximisation assumptions enabled the agents to function successfully in a richer, more complex and stable (albeit still small and closed) system. Consequently, if increasing system scale leads to the power law distribution of market shares, then the adoption of utility maximising agents would make large systems more difficult or impossible to design and maintain while implying nothing about the properties of such systems.
3 Model specification
The simulation model reported here was devised to assess conditions in which agent trading could take place in large systems and to demonstrate the constructive use of statistical signatures. The key elements of this model are:
1. The system is sufficiently large that each agent can see only a small part of it.
2. Agents can communicate directly with other agents that are known to them in order to exchange information about the existence of other agents.
These conditions suggest an analogy with “word of mouth” communication in social systems. Each agent can “see” or know a small subset of all agents. Just as people know other people who are geographically close or functionally similar to themselves, agents will see other agents in close proximity represented by direct links in a network of agents. Moreover, they will be able to find out about the existence of agents to which there is at least one path defined by agents that know other agents.
A standard representation of such a network is agents placed on a grid. If it is relevant that some agents are at the periphery of the network, then the appropriate grid is projected onto a finite plane surface. Those agents towards the edges of the plane will have direct links to fewer agents than will agents towards the centre of the plane. If such “edge effects” are not of interest, then the appropriate grid is projected onto a torus. As a first step in developing statistical signatures for systems and using those statistical signatures to identify appropriate or inappropriate agent specifications for such systems, it seems appropriate to implement the conceptually simplest possible model that has the desired system properties. For this reason, to avoid the complication of edge effects, the agent network is represented by a toroidal grid populated by agents that can “see” a limited number of cells in each of the four cardinal directions.
Moss [10] demonstrated the limitations on systems populated by rational utility maximising agents by extending the IBM model of the information filtering economy [5] in an environment represented by the unit square. Broker agents were distributed at random within the square with addresses represented by the x- and y-coordinates, information sources were distributed at random along one edge (x=0) and customer agents were distributed at random along the opposite edge (x=1). The model reported here retains the structure and the parametric settings of the extended IBM model with viable brokerage and efficient trading except that the sources and all agents (both brokers and customers) are placed at random on the toroidal grid and the agents have limited horizons.
3.1 Model structure
Cognitive agents in the model buy and/or sell items. These items are represented by the values of digits in an ordered list – a digit string. This could be a bit string (if the allowable digits are 0 and 1) but, in general, the values of the digits in the string can be to an arbitrary base. At each trading cycle, an abstract agent produces a digit string. The values of the digits represent information. The length of the string is constant over each simulation run and is determined at the start of each run by the model operator.
There is a user-determined number of item sources distributed at random on the grid. Each source holds the current values of digits at specified positions in the digit string. These values change as the system digit string changes.
The brokers are cognitive agents that acquire the values of digits from sources. These values can be acquired only as packets of all items held by a source. However, the brokers can sell items individually or in any combinations available to them. That is, they can “break bulk” by selling on to other agents only those items from a source that the other agents demand and they can combine the items acquired from several sources. The number of broker agents entering the market at each time step (the trading cycle) is chosen at random from the [1, B] interval where B is set by the model operator. Each broker begins life with no assets and builds asset reserves from profits on the purchase and sale of items acquired either from sources or from other brokers. A broker leaves the market when its asset reserves are exhausted. One consequence of this specification is that a broker’s sales revenue must exceed the cost of its acquisitions in the first trading cycle of its life.
Each broker agent is initially allocated to an empty cell but can choose to move to some other cell if it is unoccupied and no other agent is seeking to move at the same time to the same cell. The motivation to change cells is the knowledge that there is a profitable broker in the neighbourhood of the destination cell.
Customers are cognitive agents that either acquire packets of digit values from sources in the same way as do the brokers or they buy demanded items from the brokers or some combination of these. The customer agents each inhabit a given cell during the whole of the simulation run. Although the number of customer agents is determined at the start of each run by the model operator, their locations are determined at random.
At the start of each simulation run, customer agents are allocated demands for the values of digits at specified positions in the system digit string. The number of items demanded is determined at random from the [1, C] interval where C is set by the model operator at the start of the simulation run. Brokers have no demands of their own but only demands for items for which they have previously received enquiries from customers or other brokers.
Brokers and customers are synchronous, parallel agents. To enable them to communicate with one another, a series of communication cycles is nested within each trading cycle. A limit of eight communication cycles was allowed within each trading cycle though there would have been fewer communication cycles if all demands were filled earlier. In practice, this never happened in the experiments reported here.
3.2 Agent cognition
There are two principle aspects to the representation of agent cognition: the problem space architecture taken from Soar [6] and ACT-R [2] and the endorsements mechanism as adapted from Cohen [4]. The problem space architecture is described in Fig. 1.
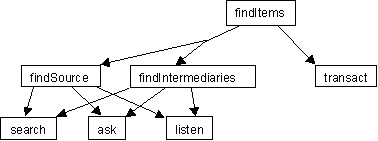
Fig. 1. The cognitive agents’ problem space architecture. The goal was to find items in demand. The initial subgoals were to find sources and find intermediaries with the further subgoals to search over the visible cells, to ask suitable agents known to the agent and to listen for their requests or replies to the agent’s own requests. Once answers had been heard, if those answers provided suitable information about available items from either sources or intermediaries, then the agent would adopt the transaction subgoal.
The urgency of acquiring any particular item – the value of the digit at any particular position in the system digit string – was determined by endorsements. Items that changed frequently in value were valued more highly than items that changed infrequently. The frequency of change was learned by experience and was in fact determined by a mutation probability. The maximum mutation probability and the (tanh) distribution of probabilities among positions of the digit were set for the duration of the simulation run by the model operator.
The choice of broker, when there was a choice, was also determined by endorsements. Brokers that were known to the agent and had been reliable in the past or relatively inexpensive and that provided most or all of the items demanded by the purchasing agent were preferred to agents that lacked any of those endorsements. A fuller description of the endorsements mechanism as used in the model reported here is to be found in several papers (e.g., [8], [9], [10],[11]).
The goal setting and actions taken in each goal and subgoal took place within communication cycles. There were two alternative specifications. In one, all of the rules were fired within the communication cycle making use of the assumptions mechanism of SDML [8]. The SDML assumptions mechanism ensures that the rules firing for any agent at any time step are sound and consistent with respect to strongly grounded autoepistemic logic. However, the rules implemented in the present model required considerable backtracking by the assumptions mechanism to ensure that no contradictions emerged. Once the logical issues were resolved, a further level of time steps – the elaboration cycle -- was specified within the communication cycle so that one layer of problem spaces was handled in each of these lower level time steps. This procedure effectively makes the problem space architecture more procedural and, by avoiding backtracking, considerably increases the speed of each simulation run.
3.3 Communication among agents
In order to concentrate on the effects of word of mouth communication, agents were not programmed to broadcast information. Direct communication among agents in SDML takes the form of the sending agent placing the desired clause on the database of the receiving agent. Because agents are parallel, synchronous agents, it is not feasible for one agent to change the state of another agent while that other agent is changing its own state. Consequently, SDML allows parallel agents to access clauses placed on their databases by other agents only at the following common time step – in the case of the present model, at the subsequent communication cycle.
Being able to follow links from one agent to another to get or give information is effectively word-of-mouth communication. One agent can communicate with another agent within its horizon. If the second agent informs the first agent of the existence and address of a third agent beyond the first agent’s horizon, then the first agent will be able to communicate directly with that third agent. If the third agent informs the first agent of the address of a fourth agent, then communication from the first to the fourth agent becomes possible. This procedure was implemented for consumer agents to engage in word of mouth communication concerning the locations of both brokers and sources. Broker agents lacked the functionality to pass on that information since it would be commercially valuable to them.
3.4 Parameter values
All of the simulation runs employed parameter settings that were taken exactly from runs of Moss’ [10] unit-square model. The system digit string contained 40 digits; there were 15 sources and 100 customers. Each customer could demand up to 12 items and each source could hold up to 15 items.
The permitted number of entrants as brokers in the market was shown in the unit-square model to have no effect on the efficiency of intermediated exchange. The maximum number of broker agents that could enter the market in any trading cycle was therefore set at 15 which is rather higher than in the runs with the unit-square model. The choice of a larger number of entrants was motivated by the intention to investigate the effect of word of mouth communication among agents: with more brokers in the market there was more information for customer agents to communicate by word of mouth.
In all runs, agents could identify the existence of sources or other agents within eight cells of their own position in the cardinal directions (up, down, right and left).
The only parameter setting that was changed for the different simulation runs was the size of the grid. Three grid sizes were used: 50´50 (2500 cells), 30´30 (900 cells) and 25´25 (625 cells).A larger grid size implies a lower density of agents.
4 Simulation results
Experimentation confirmed that agent density is a critical factor in the viability of agent trading, more surprisingly that a high proportion of demands are satisfied only when virtually all trading is via intermediary agents and that the power law distribution characterises market shares among trading agents when intermediation is viable. The results presented in this section bring out the relationship between agent density and, in turn, market effectiveness, pricing, the extent of intermediation and the nature and role of the statistical signature.
4.1 Market effectiveness
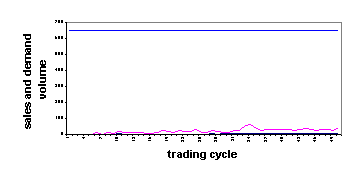
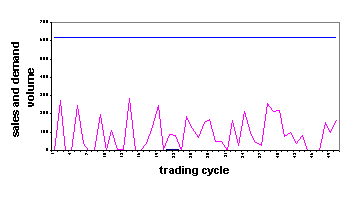
One natural measure of the effectiveness of markets is the proportion of total customer demands that are satisfied through transactions. The time series of these proportions for three scales of grids are shown in figure 2. The population density of customers and sources increases from figure 2a down to 2c. With a density of one customer in every 25 cells, as in the run reported in figure 2a, on average 3.2 per cent of demands were filled. With one customer for every nine cells, the percentage of filled demands rose to 14.6 per cent but the supplies were very erratic. The reason for the erratic nature of the supplies was that brokers typically found sources for items that potential customers wanted but the number of such items was sufficiently small that the revenue typically did not cover the transportation and storage costs. The survival of brokers in the environment modeled here, as in the unit-square environment [10], requires each broker to be able to sell on to several customers the same items obtained from a small number of sources. In that way, the transportation charges to a point close to the customer agents as well as the storage or processing charges are incurred once for a relatively large number of sales. This enables the broker to undercut the cost to the customer of acquiring the items directly from sources because the broker is able to share out the same costs among several customers.
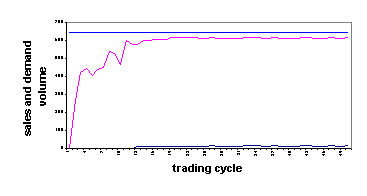
In figure 2c, it is apparent that the density of one customer for every 6.25 cells results in a high and relatively constant percentage of satisfied demands. The increase in the proportion of demands satisfied over the first 13 trading cycles is due to the appearance and survival of new broker agents and the spreading knowledge of their existence by word of mouth among customer agents.
These results extend those of Moss [10] who found in the unit-square model that intermediated exchange could take place only if the number of customer agents was large in relation to the number of sources. In this case, the same number of customers and sources were active in all simulations as were active in the best functioning markets in the unit square. The difference of course is that in the unit square model every agent knew of the existence and location of every other agent and every source. Consequently, we infer that a second condition for intermediation to be viable is that the density of agents in the market exceeds some critical level where density is defined on the number of agents known on average to each individual agent.
a) 50´50 grid (2500 cells) |
|
b) 30´30 grid (900 cells) |
|
c) 25´25 grid (625 cells) |
Fig. 2. Sales volumes in relation to demands at agent densities as determined by grid sizes
4.2 Prices
When agents are distributed so densely that every agent knows every other agent and also knows every source, then the customer agents can compare the cost of items from intermediaries with the cost of acquiring them directly from sources. Provided that customer agents always choose the cheaper source, broker agents will have to keep their prices sufficiently low that the total costs of exchange in the system are less than they would be in the absence of intermediation.
Once the density is attenuated in any way, the choice for customers is no longer whether they engage in direct exchange with the sources or intermediated exchange with brokers. The choice becomes one of trading or not since, at less than the highest densities, not all sources will be known to all customer agents. In this case, unless some expenditure constraint is imposed on the customer agents, there is nothing to limit price. Increasing rates of price inflation were indeed encountered in the 625-cell simulation but these obviously had no effect on the volume or stability of trade.
No attempt was made in these models to introduce price competition among brokers although the customer agents did positively endorse brokers they knew to be cheaper than others and, so, other things being equal, would choose the brokers offering lower prices. At the same time, they valued reliability – orders translating into deliveries – more highly the cheapness.
We conclude that, while price competition and low prices generally are doubtless important features of some systems (for example, real societies), price competition is not a core consideration for the functioning of exchange processes in large systems.
4.2 The extent of intermediation
Demand satisfaction in all of the modelled markets was very largely a result of intermediated transactions. In Figure 2, the time series in each case represents, from the bottom up, acquisitions of items by customers directly from sources and the total of satisfied demands. The horizontal topmost line is total demand. Evidently, in all cases direct acquisition from sources was negligible.
In the most successful (most densely populated) market, intermediary agents were not on average very long lived and, as indicated in Figure 3, there were always a large number of broker agents.
Because there was a stream of broker agents entering the market, each of them would attract demand enquires from and make supply offers first to agents within their visibility horizon and would communicate with increasingly distant customer agents as knowledge of their existence spread by word of mouth. Consequently, their customers would tend to be relatively close to them. This gives scope for a larger number of brokers to be active in a large system than in a small system (i.e. a system where every agent knows every other). As is seen from figure 3, once the market became established, the effective system was marked by a gaggle of brokers. The size distribution of these brokers (by sales volume) is the subject of section 4.4, following.
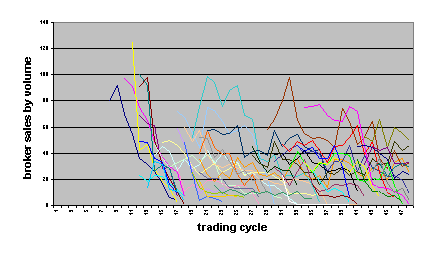
Fig. 3. Intermediaries’ sales volumes in a 25´25 (625 cell) grid
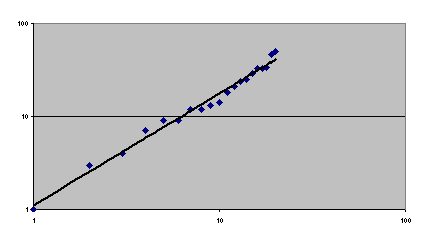
Fig. 4. Intermediaries’ sales obey the power law, in this case in the 50th cycle of a simulation run.
4.4 The power law distribution
The power law is obeyed when equation (1) describes the relationship between a cumulative distribution and the rank of an object when the objects are ordered by size. It is clear from figure 4 that the power law holds for cumulative sales volume against the rank of the broker (from lowest to highest sales) at the 50th trading cycle of the simulation of the 625-cell market. That the power law was obeyed consistently during the trading cycles is shown by figure 5 and table 1. Figure 5 shows the trend lines of the power law data for every ten trading cycles from the 20th cycle. The intercepts and slopes of the trend lines for the 20th and 30th cycles are not distinguishable at the 95 per cent confidence level. The trend lines for the 40th and 50th cycles are significantly different from each other and the other two. In all cases, of course, the slopes are significant and positive indicating that, however many intermediaries are active in the market and despite the finding that none of them are long lived, there is always a substantial monopolistic element. This result is not different from the results with the unit-square model.
|
trading |
a |
b |
R-square |
|
19 |
-0.73751 |
1.555198 |
0.953736 |
|
29 |
-0.44535 |
1.477288 |
0.988578 |
|
39 |
-0.90515 |
2.042664 |
0.942295 |
|
49 |
0.04263 |
1.204543 |
0.983854 |
Table 1. Regression estimates of power law: log y = log a + b log x demonstrate that the power law holds but the particular distribution changes over time in no systematic way. The exponent b is not significantly different in the trading cycle 29 from the value in trading cycle 19, but they are significantly diggerent a 90% confidence from either of the other two which are themselves significantly different.
5 Implications for agent research
The simulation model and analysis reported here has one implication for agent architectures and the effectiveness of large multi agent systems, one implication for MAS requirements analysis and one implication for agent theory.
The implication for the effectiveness of multi agent systems that are large in the sense that it is not feasible for every agent to encounter every other agent in real time is that word of mouth communication among agents can make the system function effectively provided that there is some minimum density of agents in the system. There is no necessity for a blackboard system to support communication.
The implication for MAS requirements analysis is that statistical properties or signatures of real systems is a useful guide to simulation analyses to the ability of full-scale systems to function as intended. The generation of power law distributions is one example, another for which there is currently a vogue is the small world property.
The implication for agent theory is that the specification of utility maximising agents will not support an analysis of the properties of large, distributed systems if those systems are to mimic market systems as described by equilibrium economic theory. This result, based on the observation of power law distributions and a formal theorem of mathematical economics, indicates that it is possible and desirable to identify statistical signatures that inform the selection or rejection of agent theories.
It is always important to remember that simulation experiments suggest possibilities. We will obviously have more confidence in the generality of results that are found from a variety of simulation experiments designed and developed independently and run on different platforms. The results reported here do no more than to identify relationships and propositions that arguably deserve further analysis and experimentation to determine the extent, if any, of their validity.[1]
References
[1] Adamic, Lada A. and Bernardo A. Huberman. The Nature of Markets in the World Wide Web, Xeros Palo Alto Research Center, 1999.
[2] Anderson, J.R. Rules of the Mind. Lawrence Erlbaum Associates, 1993.
[3] Axtell, Robert. The Emergence of Firms in a Population of Agents. Working Paper 03-019-99, Santa Fe Institute, 1999.
[4] Cohen, Paul R. Heuristic Reasoning: An Artificial Intelligence Approach. Pitman, 1985.
[5]Kephart, Jeffrey O., James E.
Hanson, David W. Levine, Benjamin N. Grosof, Jakka Sairamesh, Richard B. Segal
and Steve R. White. Dynamics of an Information-Filtering Economy. In Proc.
Second International Workshop on Cooperative Information Agents (CIA-98).
[6] Laird, J.E., A. Newell and P.S. Rosenbloom. Soar: An Architecture for General Intelligence. Artificial Intelligence, 33: 1-64, 1987.
[7] Lipsey, R. G. and Kelvin Lancaster. The General Theory of the Second Best. The Review of Economic Studies, 24:11-32, 1956.
[8] Scott Moss, Helen Gaylard, Steve Wallis and Bruce Edmonds, SDML: A Multi-Agent Language for Organizational Modelling. Computational and Mathematical Organization Theory, 4: 43-69, 1996.
[9] Scott Moss. Critical Incident Management: An Empirically Derived Computational Model. Journal of Artificial Societies and Social Simulation, 1, <http://www.soc.surrey.ac.uk/JASSS/1/4/1.html>, (1998).
[10]Scott Moss. Applications-Centred Multi Agent Systems Design with Special Reference to Markets and Rational Agency. In Proceedings of the 4th International Conference on Multi Agent Systems, 2000.
[11]Scott Moss. Canonical Tasks, Environments and Models for Social Simulation. Computational and Mathematical Organization Theory, 6: in press, 2000.
[12]Vilfredo Pareto. Cours d’economie politique. Lausanne,
1896-7.