Achieving Consensus Among Agents
– an opinion-dynamics model

Bruce Edmonds

Centre for Policy Modelling, Manchester Metropolitan University
Aytoun Building, Aytoun Street,
Manchester M1 3GH, UK.
+44 161 247 6479

bruce@edmonds.name

ABSTRACT

The paper considers the problem of how a distributed system of agents (who communicate only via a localised network) might achieve consensus by copying beliefs (copy) from each other and doing some belief pruning themselves (drop). This is explored using a social simulation model, where beliefs interact with each other via a compatibility function, which assigns a level of compatibility (which is a sort of weak consistency) to a set of beliefs. The probability of copy and drop processes occurring is based on the increase in compatibility this process might result in. This allows for a process of collective consensus building whilst allowing for temporarily incompatible beliefs to be held by an agent. This is an example of socially-inspired computing (by analogy with biologically-inspired). The space of behaviours in a MAS where agents interact with each other at the same time as reasoning/learning themselves is so vast that a "structuring idea" is needed. Here we apply an analogy with human opinion-dynamics as an analogy with which to design, manage and understand a subset of this huge space. Results suggest that a reasonable rate of copy and drop processes and a well connected network are required to achieve consensus, but given that, the approach is effective at producing consensuses for a sample of randomly defined compatibility functions. However, there are some belief structures where this is inherently difficult to achieve.   The results are compared to those from the simple opinion dynamics models, and some tentative hypotheses about agent consensus in this model posited.

Categories and Subject Descriptors

I.2.11 Distributed Artificial Intelligence - Multiagent systems, Coherence and coordination

General Terms

Algorithms, Management, Reliability, Experimentation.

Keywords

Simulation, agent-based, socially inspired, consistency, opinion dynamics, belief revision, meme, consensus.

1. INTRODUCTION

Consider a community of agents in an uncertain but common environment who are each trying to work out what to believe about this environment.  For example, imagine a pest control scenario: a number of robots are deployed to eradicate a certain pest, where each robot has a menu of possible actions but it is not known which combination of these actions is effective (indeed if any are).  The problem is here how these robots should exchange their own uncertain knowledge in a distributed and scalable manner even though, due to their different experiences, the robots will have different beliefs about which combinations should be deployed.  This is a hard problem since there may be complex interactions between the action choices, for example where action A together with action B (i.e. {A, B}) is desirable or {B, C} but not {A, B, C} or {A, C}.  Furthermore, each robot may have different evidence for each of these combinations, and hence come to a different conclusion to its peers.  Thus in this problem there needs to be some social process of information exchange to pool the knowledge gained, but whilst allowing each robot to come to some reasonable conclusion about what it judges is the best combination.  Thus there are potentially complex interactions between the social and the individual processes here, which makes it difficult to foresee the outcome.

Of course, all the separate items of knowledge of all the robots might be assessed together in some central agent which would then come to a conclusion (at any particular time) about the best combination of actions and send this as instructions to each agent.  However this, centralised solution, might not be feasible or appropriate in many circumstances (for example where it is not possible to communicate except with neighbours).  This paper looks at only at such distributed processes where each agent has essentially the same algorithm and access only to its own information and that sent to it by its immediate neighbours. 

However understanding such linked systems of individual reasoning and/or learning in conjunction with such social interaction is extremely difficult even in specific cases and probably impossible in general (based on results such as ....).  The approach to be followed in this paper is to use ideas derived from the social sciences in order to get a handle on a particular range of agent behaviours, in a systematic and guided manner.  The analogy with human society provides a guideline or “theory” for understanding what is happening in a particular range of MAS that can be used to design and/or manage such systems.  Here an agent-based simulation makes this theory precise to enable the consequences of different set-up to be explored.  This does not mean that there may not be more efficient ways of achieving the same ends in ways other than those that occur in human society, but rather that using a well understood idea and precise instantiation, in terms of a simulation model, may enable us to achieve some design and maintenance goals for MAS in a more systematic and reliable manner.  This follows other such work in human-inspired MAS work which is discussed in Section 5.

This paper describes a model that, although inspired by a series of social simulation models, had been designed to be specifically applicable to the global behaviour of a group of locally interacting agents with some reasoning and learning capacity.  There have been a series of opinion dynamics models in social simulation, and sociophysics, which attempt to explain the process of consensus forming, the drift to extremes in terms of social processes which is discussed in Section 4.  However these represent the state of the nodes representing agents in terms of a binary opinion or a floating point number indicating their strength of opinion on a single issue.  This model grounds the model more in specific beliefs that spread around the network and interact via an agent belief revision process.

2. MODEL DESCRIPTION

2.1 Outline

The aim of this model is to capture a subset of the possible outcomes of a set of locally interacting agents, each of which is separately updating its set of beliefs in parallel with the influence of one agent upon another.  The idea of this model is that will be applicable as a rough model of a distributed set of agents, but one where knowledge is uncertain.  It is assumed that there is a background of shared beliefs that are not represented in this model, but against which (as well as evidence from interaction with the environment) the “foreground”, represented beliefs are judged.  In this we try to be as uncommitted (or as flexible) as possible to the structure and relationship between beliefs.

In this model there are a number of agents who are connected via a network.  Each of these agents either has a separate set of beliefs drawn from a set of possible beliefs – that is each agent either believes or does not believe each of a fixed universe of beliefs.  The beliefs are not independent of each other – that is different combinations of these will be more or less compatible as a collection.  Thus there will be collections of beliefs that are highly incompatible with each other – what might be called inconsistent in a situation where beliefs were certain.  In such circumstances an agent might drop a belief to improve its compatibility.  Likewise there will be collections where adding a new belief will greatly increase its compatibility.

Thus there are two processes where beliefs are changed:

1. The copying of beliefs from connected agents along the network of connections (copy)

2. The dropping of beliefs by an agent (drop)

Both of these processes is more likely to happen if the result of the process is an increase in the compatibility of the resulting belief set.  A third process could be the individual acquisition of beliefs by a single agent, but this is not explored here because the paper concentrates on the short-term dynamics of agreement among the agents. 

2.2 Belief Compatibility

The compatibility of a belief set is given by a simple function from the set of possible beliefs into the interval [-1, 1].  A value of 1 indicates ultimate compatibility; 0 a neutral set; and a value of -1 indicates ultimate incompatibility.  The exact meaning in terms of any modelled system of agents is left deliberately undefined.  It could be that 1 indicates simple consistency and -1 inconsistency, but given that we are here dealing with uncertain knowledge I want to leave all possibilities open – to be determined by the specific system being modelled.  For example it may be that belief in a certain proposition and its negation might be useful in the short term as beliefs are being propagated around the network, only to be more gradually resolved over time as a result of the interactions of the whole group of agents.  The range of values within [-1, 1] may indicate a judgement of their compatibility in the presence of much uncertain knowledge, where precise reasoning and hence judgements are not possible.

Thus, if P is the set of possible beliefs, , there is a function:  so that whether a change in belief occurs from to is influenced by the value of , that is the copy and drop processes tend to occur to increase belief compatibility, called the compatibility change.  In the version of the model reported here the probability of either of the above processes is determined by this value.  A simple example of this function could be one that gives any belief set a value of 1 if it is consistent and -1 if it is not – this would correspond to a simple binary classical logic.  Other functions would encourage different belief structures and, depending on the interpretation of the logical relations between the basic beliefs in P, correspond to different logics.  In some of the results below randomly assigned compatibility functions are used and in other a selection of simple specified ones for comparison.

2.3 Model Set-up

The model reported here is a specific instance of that described above.  In particular, there are a fixed number of nodes with a random but fixed communication network between them.  Each node represents an agent.  The compatibility function is fixed. After the initial random distribution of beliefs only the copy and drop processes are employed and these use a rule for determining the probability of the copy and drop processes occurring given the potential compatibility change.

Thus there are n agents, with m bidirectional arcs randomly assigned between them.  There are p possible beliefs, i.e. P is of size p.  Each possible subset of P is assigned a value in [-1,1] by the compatibility function,  f (in many cases below these values are assigned randomly at the start of a run).

At the start of a run, each member of P has a fixed probability, i, of being assigned to each node, i.  After that single beliefs (i.e. members of P) are either copied along arcs or dropped from nodes according to the copy and drop processes.  The drop and copy processes that occur each iteration of the simulation are specified in Figure 1, Figure 2 and Figure 3 below, where B(a) is the belief set of node a.

Figure 1. The copy process

The scaling function, c(D+1)/2, simply maps the [-1,1] compatibility function to [0,1] to be a suitable probability, moderated by the copy rate, c.  Clearly this mapping is fairly arbitrary and others could be tried.

Figure 2. The drop process – unconditional version

Though there are two variants of the drop process, one as above and the second which comes in to play only if the current belief set has a present compatibility less than zero.  The idea of this is that an agent might only decide to drop a belief if the set was incompatible to an unacceptable degree (i.e. inconsistent).

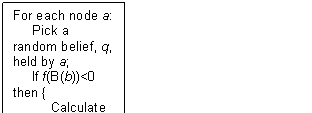
Figure 3. The drop process – conditional version

Where c and d are parameters of the model controlling the copy and drop rates respectively.  The parameters of the model are as follows with  their ranges, the bracketed value is default value in all the below these can be assumed unless otherwise specified:

· Number of nodes, n, [1...¥] (10)

· Number of arcs, m, [0…¥] (20)

· Number of possible beliefs, p, [1...¥] (3)

· The copy rate, c, [0,1] (0.5)

· The drop rate, d, [0,1] (0.5)

· The initial probability of a belief occurrence at any node, I, [0,1] (0.5)

· Arc type, {Un=unidirectional, Bi=bidirectional} (Bi)

· Type of drop process {Con=conditional, Unc=unconditional} (Con)

· The values of the compatibility function for each possible subset of P, each in [-1,1] (randomly assigned)

· The network topology – in every case below the network topology has been randomly assigned, that is the required number of arcs randomly selected without replacement from all possible arcs, but excluding arcs from a node to itself.

3. RESULTS

3.1 General Results

Two measures of the results are displayed here.  The first is an indication of the belief set that that agents converge to (if they do) called the weight and the second is the number of nodes with the most common belief set.

The weight is just a way of mapping the distribution of different possible belief sets onto [0,1] for ease of graphing and comparison.  It is calculated as follows:

The i^th member of P is given the value of ; the value of a node is the sum of these values scaled by the greatest possible sum; the weight of the complete system is the average of the node values.  Thus in the case where P={A, B, C} (the case in many runs): A has value 1, B 2, C 4; the greatest possible sum is 7, resulting in the following values:

Belief Set	Weight
{}	0
{A}	0.14
{B}	0.29
{A,B}	0.43
{C}	0.57
{A,C}	0.71
{B,C}	0.86
{A,B,C}	1

Table 1.  Weights for various belief sets

The second measure is simply the size of the set of nodes with the most commonly occurring belief set, so that if consensus is achieved the value is n (usually 10) and if the most common set is at only 3 nodes, its value would be 3.  This measure will be called the consensus.

In all cases below the model was run for 25 times for each setting for 200 iterations of each setting.  The graphs show the averages of the above measures sampled every 5 iterations over time – thus the x-axis in all the below graphs is that of time.  The short-term evolution of the consensus was focused on due to its relevance to its intended field of application – it is unlikely that any environment or situation such agents inhabit will remain static for long enough for long-term trends in consensus forming to be relevant.  If not otherwise stated the results shown below are using the default settings listed with the parameters above.

To illustrate that the nodes do tend to converge regardless of the exact network topology Figure 4 shows the weights of 14 different runs of the model with different random initialisations and networks each time.  This was actually run 100 times but the diagram with 100 lines on it is difficult to make out, by 30 iterations all but a small minority of networks have converged, by iteration 100 all of them.  In contrast the compatibility function is critical to the convergence, as Figure 5 illustrates.  Here 14 (again out of 100) traces of average weight are shown, all with the same network, but different compatibility functions.

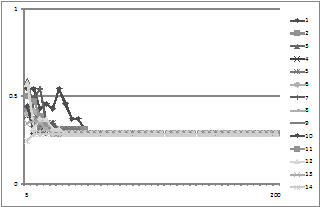
Figure 4. The evolution of average weights for 14 different runs with the same compatibility function but different networks

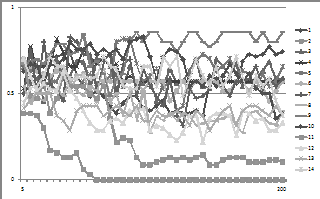
Figure 5. The evolution of average weights for 14 different runs with the same network but different compatibility functions

Of course, if the network is sufficiently sparse as to be disconnected (or only have parts that are distantly connected) then this will prevent or delay the achievement of consensus.  This is show below in Figure 6 where the average consensus for different numbers of arcs is shown (always 10 nodes).

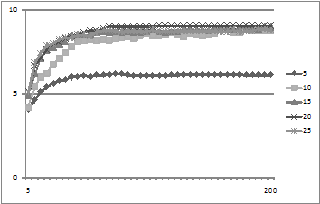
Figure 6.  The average degree of consensus given different numbers of arcs

Here 5 arcs means there will be disconnected parts of the network, 10 means it is almost always connected and 15 and above pretty much ensures it.  In fact Figure 6 seems to suggest that over-connection can slightly reduce consensus, but allowing too much “churn” as the result of copying.

Figure 7 is a similar graph for varying copy rates.  Clearly some copying is necessary if consensus is to be approached, but rates above 0.4 did not speed up the process.

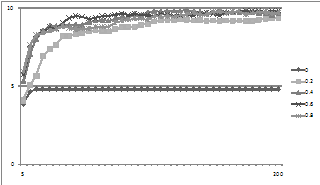
Figure 7. The average degree of consensus given different copy rates (c) using the same network but a random sample of compatibility functions

In Figure 8 a similar graph for changing drop rates is shown.  A drop rate of 0 obviously leads to a fast consensus, but then the consensus arrived at will be pretty arbitrary.

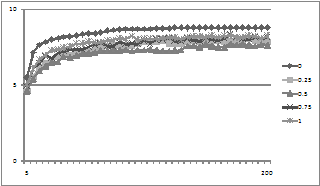
Figure 8. The average degree of consensus given different drop rates (d) using the same network but a random sample of compatibility functions

Finally in this subsection we show the effect of varying the number of possible beliefs (i.e. p).  Clearly the more possible beliefs the harder it is to reach consensus and the longer it takes.

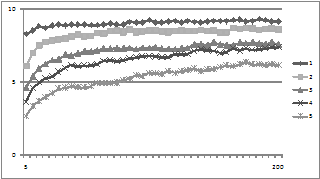
Figure 9.  The average degree of consensus given different  numbers of possible beliefs

To sum up: a reasonable rate of copy and drop processes and a well connected network are required to achieve consensus, but given that the approach is effective at producing consensuses for a sample of randomly defined compatibility functions.  The next subsection looks at the system behavior for specific functions.

3.2 The Effect of the Compatibility Function

Whilst the above results give an idea of the general characteristics of this model, it is difficult to discern the effect of the compatibility between beliefs.  Thus here we compare the effects of 5 different compatibility functions over a variety of conditions.

Fn	{}	{A}	{B}	{C}	{A,B}	{B,C}	{A,C}	{A,B,C}	Max weights
zero	0	0	0	0	0	0	0	0	0-1
decr	1	1/3	1/3	1/3	-1/3	-1/3	-1/3	-1	0
incr	-1	-1/3	-1/3	-1/3	1/3	1/3	1/3	1	1
sing	0	1	1	1	-1/2	-1/2	1/2	-1	0.14-0.57
dble	-1	0	0	0	1	1	1	-1	0.43-0.86

Table 2. The 5 explicitly defined compatibility functions and the weights for an ideal consensus

Where zero, decr, incr, sing and dble are shorthand for zero, decreasing, increasing, single and double compatibility functions respectively. The last column in Table 2 indicates the weight (or weights) that will be achieved by all nodes if they settle on the belief set with the greatest compatibility.  The single and double compatibility functions are difficult for a network because in each case a number of different maximally compatible sets are possible, but where copying between nodes with these sets will cause a decrease in compatibility.  The zero function is a base comparison case as all belief sets are equally indifferent as to compatibility.  In addition a sample of randomly assigned compatibility functions are also tried to aid comparison with the previous results.

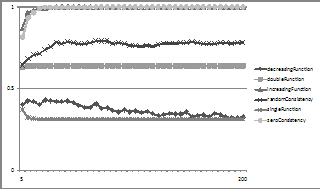
Figure 10. The average weights for the different compatibility functions with conditional dropping

Here we see the average weights converging to what we expect, with the exception of the decreasing function which gets stuck away from the optimum.  This is because beliefs are only dropped if the compatibility is less than zero and this function gives a positive but sub-optimal value for singleton sets.

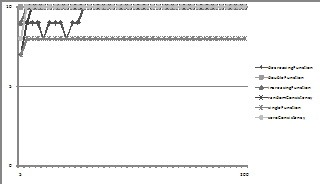
Figure 11.  The average degree of consensus for the different compatibility functions with conditional dropping

Here we see a rapid development of consensus except sometimes for the single function which can get stuck in a situation where different groups of nodes have finalised on different belief sets (in this case different singletons) no copying then occurs because the probability of that given by the copy process is zero.

Compare this to the same set-up but where the dropping process is purely probabilistic (i.e. unconditional) in the below graphs.

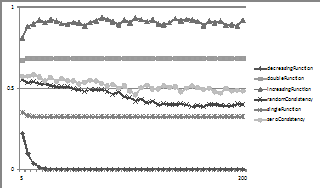
Figure 12.  The average weights for the different compatibility functions with unconditional dropping

In this case the cases with the decreasing function rapidly reach their optimal value but those of the increasing function do not.  This is because there is always a finite probability that with the increasing function a node with {A,B,C} will drop one of its beliefs temporarily (until it is re-copied from a neighbour).

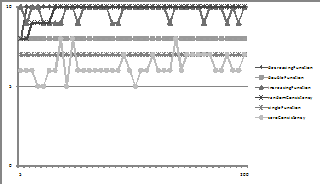
Figure 13.  The average consensus for the different compatibility functions with unconditional dropping

The unconditional dropping results in a slower rate of consensus.  Indeed the double, single and zero function systems often did not reach consensus.  The zero function system in this version is, of course, subject to essentially random drift.

If the network is unidirectional we get essentially the same tendencies in terms of the belief sets the systems converge to, except with the zero function which indicates that this causes a different background bias/drift.  However the rates and way in which consensus is reached.  Taking the equivalent situation as Figure 11 but arcs being unidirectional we get the below.

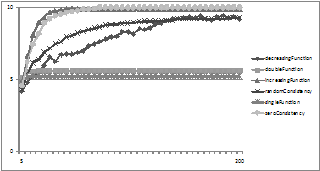
Figure 14.  The average degree of consensus for the different compatibility functions with conditional dropping but with unidirectional arcs.

The similar case for unconditional dropping is as follows.

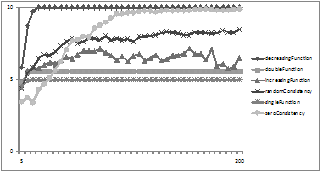
Figure 15.  The average degree of consensus for the different compatibility functions with unconditional dropping but with unidirectional arcs.

Comparing Figure 14 and Figure 15 to Figure 11 and Figure 13 respectively we see that restricting the arcs to being only unidirectional slows the rate of consensus building and, indeed for some functions seems to prevent it altogether.

To sum up these result. On the whole the process resulted in the optimal belief set, but there are some belief structures where this is inherently difficult to achieve – those like single or double where there are several equally compatible belief sets where copying between different sets in adjacent nodes reduces the recipient’s compatibility.  Given this observation, clearly some compatibility functions are dealt with by different structures and setting – there does not appear to be a universal way of getting rapid consensus to optimal belief sets for all belief structures.

4. RELATED WORK

There have been a stream of opinion-dynamics models in socio-physics and social simulation, going back to [7].  Early models were based on the standard Ising model with each node having a binary “spin” or opinion [10], [17].  Later [3] and [15] introduced a model with a continuous opinion, based upon the principle that nodes with similar opinions will become more similar if they interact. These models were based upon the random interaction of its components.  [14] reports a discretised version of this model, this found similar results as the continuous version. [4] summarises some of the many results in this field and also looks at the different behaviour that comes from interaction within a regular lattice.  However none of these models have been designed with modelling the adjustment between agents in a localised network in mind.

The work here could be seen as fitting into the general framework proposed in [1], except for the fact that there are no goals in this model (except the implicit one of achieving consensus with its neighbours and a compatible set of beliefs).

[16] reports upon a system which attempts to use agents to iteratively achieve consensus by using a voting mechanism using variations of syntactic similarity matching.  The compatibility function here could be compare to their measure of syntactic similarity, but the interaction in this was global, being based upon a voting model.

5. CONCLUSION

Due to the possibility of emergence in complex MAS, formal specify and design methodologies are not enough to obtain systems with desirable properties [6] and hence an experimental method is, to some extent inevitable as well as being feasible [7].

This work is part of a growing band of work that could loosely be characterised as “socially-inspired” computing.  This is where ideas taken from the social sciences or suggested by observation of human societies are used as a analogy to guide the construction and understanding of distributed systems.  It can thus be seen as intending to be part of the program illustrated in [8]  and  [11], with a model that is more applied than the above abstract socio-physics models but being simple enough that its behaviour can be explored using simulation. 

In order to somewhat compensate for the lack of formality the process of model development should be staged from abstract to specific simulations and implementations.  Each stage in this process (which is comparable to the refinement and development of specifications) can be seen as a theory for the next more specific model and used to check some of its properties.

Here the important processes of how a locally connected set of agents where social and individual belief revision processes occur have started to be investigated.  Suggestions from models such as this may be crucial in determining the structure of more specific systems of agents with desirable properties, such as the ability to adapt and yet reach consensus about complex sets of interacting beliefs.  This is only a start on this project – a large bulk of work needs to be done.

6. ACKNOWLEDGMENTS

Some of this work is done under grant XXXX from the EPSRC.  Our thanks to participants of the EPSRC NANIA project for helpful discussion, in particular Alan McKane and Craig Thomas or the University of Manchester, Physics Department.  Also to David Hales for many discussions, David has been one of the pioneers of socially-inspired computing.

7. REFERENCES

[1] Amgoud, L., Belabbes, S. and Prade, H. (2005) Towards a formal framework for the search of a consensus between autonomous agents. AAMAS '05: Proceedings of the fourth international joint conference on Autonomous agents and multiagent systems, ACM Press, New York, NY, USA, 537--543.

[2] Belnap, N.D., Jr. (1977) How a Computer Should Think, In G. Ryle (ed.), Contemporary Aspects of Philosophy, Oriel Press.

[3] Deffuant, G, Neau D, Amblard F, and Weisbuch G (2000) Mixing beliefs among interacting agents. Advances in Complex Systems 3. pp. 87 – 98.

[4] Deffuant, G. (2006) Comparing Extremism Propagation Patterns in Continuous Opinion Models, Journal of Artificial Societies and Social Simulation vol. 9, no. 3 http://jasss.soc.surrey.ac.uk/9/3/8.html

[5] Deffuant, G., Amblard, F., Weisbuch, G. and Faure, T. (2002), How can extremism prevail? A study based on the relative agreement interaction model, Journal of Artificial Societies and Social Simulation, Vol. 5, No. 4, <http://jasss.soc.surrey.ac.uk/5/4/1.html>.

[6] Edmonds, B. And  Bryson, J. (2004) The Insufficiency of Formal Design Methods - the necessity of an experimental approach for the understanding and control of complex MAS. In Jennings, N. R. et al. (eds.) Proceedings of the 3rd International Joint Conference on Autonomous Agents & Multi Agent Systems (AAMAS'04), July 19-23, New York, ACM Press,  938-945.

[7] Edmonds, B. (2004) Using the Experimental Method to Produce Reliable Self-Organised Systems. In Brueckner, S. et al. (eds.) Engineering Self Organising Sytems: Methodologies and Applications, Springer, Lecture Notes in Artificial Intelligence, 3464:84-99.

[8] Edmonds, B., Norling, E. and Hales, D. (2007) Towards the Evolution of Social Structure.  Computational and Mathematical Organisation Theory.

[9] French, J. R. P. (1956) A formal theory of social power. Psychological Review 63. pp. 181 –194.

[10] Galam, S. and Moscovici, S. (1991) Towards a theory of collective phenomena: consensus and attitude changes in groups. European Journal of Social Psychology. 21 49-74.

[11] Hales, D. and Edmonds, B. (2003)  Evolving Social Rationality for MAS using “Tags”, In Rosenschein, J. S., et al. (eds.) Proceedings of the 2nd International Conference on Autonomous Agents and Multiagent Systems, Melbourne, July 2003 (AAMAS03), ACM Press, 497-503.

[12] Hales, D. and Edmonds, B. (2005) Applying a socially-inspired technique (tags) to improve cooperation in P2P Networks, IEEE Transactions in Systems, Man and Cybernetics, 35:385-395.

[13] Priest, G. (2002) Paraconsistent Logic, In D. Gabbay and F. Guenthner (eds.), Handbook of Philosophical Logic (Second Edition), Vol. 6, Kluwer Academic Publishers, Dordrecht, 287-393.

[14] Stauffer, D., Sousa, A. and Schulze, C. (2004) Discretized Opinion Dynamics of The Deffuant Model on Scale-Free Networks, Journal of Artificial Societies and Social Simulation vol. 7, no. 3 http://jasss.soc.surrey.ac.uk/7/3/7.html

[15] Weisbuch, G, Deffuant G, Amblard F and Nadal J P (2001), Interacting agents and continuous opinion dynamics. http://arXiv.org/pdf/cond-mat/0111494

[16] Williams, A.B., Krygowski, T.A., and Thomas, G. (2002) Using agents to reach an ontology consensus, Proceedings of the first international joint conference on Autonomous agents and multiagent systems: part 2, July 15-19, 2002, Bologna, Italy   [doi>10.1145/544862.544972]

[17] Young, P., 1998. Individual Strategy and social structure. Princeton University Press.