How To Be Loyal, Rich And Have Fun Too:
The Fun Is Yet To Come
Juliette Rouchier (GREQAM) and David Hales
(CPM) [1]
1 Introduction
Our paper presents a model that has been elaborated to synthesize the first results of a field study and simulations that were led in the artificial societies that were derived. The study is led at the “Marché d’Intérêt National des Arnavaux[2]”, a wholesale fruits and vegetables market, situated near Marseille, and which represents one of the main hubs of supply for retailers. The elaboration of prices takes place through one-to-one interactions along the morning, with only oral information being given to retailers. To elaborate its prices, each wholesale seller competes with all his colleagues of the market and is dependent on its suppliers’ offers. The indirect competitors of all retailers are the supermarket suppliers, which define the average prices Supermarkets use an alternate (and larger) supply chain.
The study of real markets is not extremely developed yet in the economics field (Kirman, 2002). Classical economic analysis deals with ideal prices that ought to appear when certain buyers and sellers, whose reservation prices are known, meet. Reservation price is a key concept in the study of markets: it stands for the minimum price a seller wants to get for the product he is selling (alternatively the maximum price a buyer is willing to give). Once ones knows all the reservation prices, it is indeed possible to know who will be able to exchange and who has expectations that cannot be fulfilled; then to build an offer and demand curve, which intersect at a value called the equilibrium price. A classical approach enables to interrogate the nature of market institutions (institutions can be for example auctions or paired interactions) by evaluating their efficiency, i.e. the total value produced compared to an ideal value with the best possible matching. An other issue is the one of information that is generated for the agents by exchanges that take place: how much does each transaction reveal of the reservation prices of the others (and hence their preferences).
Once one starts to study how information is generated and processed by individuals, it becomes interesting to study markets in real, so that to find out how individuals actually deal with dynamical offers and demands that can be expressed through transactions, price proposals, apparition of shortages. One trend is the study led by behavioural economists, who put people in artificial controlled market settings (Smith, 2002; Rabin, 2002). They observe the proposals and accepted transactions along the time, and can limit and monitor any information circulation. They analyse how prices dynamics can be related to the institution that is chosen to organise the interactions. They use comparison to establish their hypothesis: they observe real actions in different settings, where the quantity and quality of information can vary.
Another approach is the study of real markets in their natural environment, where no variable can be controlled. Whereas artificial markets enable to study the actions of individuals undergoing short-time interactions in a market activity, the observation of a living market can help understand which actual use of the official institutions humans develop and how they interact in the long term. Indeed, our interest in this study is to see how individuals adapt to their environment, but also arrange it, so that to be efficient in the long-run (Callon, 1998). This is a very different approach to more classical economy, since the motivational aspects of an everyday life activity has to be reconsidered , being necessarily far different from one shot meetings or an ideal computation based on only monetary preferences. There are indeed numerous ethnographic evidences that economic activities are not based solely on an income optimisation attitude (Sahlins, ; Malinowski, 1922). It is also shown by simulation that the motivations of economic attitude have a impact on global results in an economy (Janssen and Jager, 2001). More specifically, we are here interested in studying the apparition of habits within a certain framework, be them relational or calculative: the shape of these habits and the potential interest they represent for the actors. It is indeed common to stress the importance of networks and of the strategic behaviour of actors regarding these networks on market (Fafchamps and Minten, ?). One of the common interpretation, that we will not follow here, is related to a now classical analysis in economics, which explain the reinforcement of relational link because of their effect on the reduction of transaction costs (Poole et al., 1998).
After performing a field
study on the Marché des Arnavaux, organised as a series of observations on the
market and of interviews with wholesale sellers and retailers, we decided to
structure the results by building a multi-agent model[3].
No economic theory can help us analyse our observation, and only a few results
have been focusing on the same type of behavioural and institutional issues,
like (Kirman … ) on the fish market in
Marseille. Hence we had to produce our own assumptions on what are the
motivations for behaviour for the actors, that are based at the same time on
our field study and on sociological books that describe trading activities and
networks in the area of Marseille (Taurius, 2002). To see if the more
significant cognitive processes we identified can be described in a consistent
way, simulating interactions in artificial societies seemed to be a reasonable
first step. Afterwards, our aim is to relate our research to a larger
methodology which is increasingly used to deal ling with economical or
coordination behaviour, “companion modelling” (Bousquet et al. 1999, Rouchier
et al., 1998, Barreteau and Bousquet, 2000). The model results will be
redirected towards the represented actors, whose remarks help to reconsider the
model, and hence help to guarantee the qualitative validation of the model.
2 Studying perishable good markets
The market we study takes place every morning except on Sundays. It is made of an open space constituted of two large rows of individuals boxes where wholesale sellers display the goods they have acquired from their own suppliers (producers or importers). Goods come on the market by truck every morning from 3 to 4. Retailers come to buy their daily stock from the wholesalers after 3:30, and most of them leave as soon as they have acquired all the goods they need. At 9 am, the last retailers go away and the wholesale sellers close their shops. They then start the second part of their activity that consists in checking of their accountants work, solving problems, ordering from their suppliers or taking orders for big customers that don’t come on the market. Retailers, once they have gone away, have to go back to their shop or their market, put all the products in a nice disposition and establish their prices, so that to be ready for the first customers to arrive.
In this work we are only interested in representing the interactions that take place on the market, although the existence of network regular relations with big customers (like schools or boat catering companies) are very important in the survival of the wholesale sellers companies as well as their ability to establish their prices.
2.1 Retailers
Most retailers go there every morning or every second day to buy the goods they need for their customers. Fruit and vegetables are perishable and keeping them a few days requires quite heavy infrastructure. That’s why retailers tend to come very regularly to have the freshest products they can. It is very important for them to provide their customers with a range of products that is sufficiently diverse and where the goods are present in a regular way, even though there are sometimes unpredicted shortages. They can also profit of oversupply by getting very cheap goods and sell them to attract clients. Their first interest is thus to find the product they need, and then to find it for the cheapest price.
The constraint of continuity in products forces them to have habits on the market itself: either they go to certain wholesale sellers who always have a wide range of products or they have relations with several sellers who will help them fulfil their needs as well as they can. In there case, having a friendly relation with a seller can enable them to order from one day to another, or to know about shortages to come a day in advance.
The other constraint for the buyers is time. Most of them have to go back to their shop as early as possible to have their fruits ready for the first customers. Hence, they need some information on the market situation but cannot go around indefinitely. In this market, there is no global information for the current day, but an estimation of the average price is officially displayed for each product. Sellers display no prices and transactions are always preceded by negotiations. To get information, buyers can visit several wholesale sellers, or alternatively ask some of their friends who has visited other sellers. Usually, retailers spend some time in the bar, discussing with others, or use their cell phones to ask prices to their friends.
The surveys showed that there are two main type of behaviours, which are close to what Kirman has described in his work on the fish market: either retailers are very loyal and go regularly to the same seller, or they use the potentiality of the market to identify the best prices and compose their basket by buying at different shops. We had no opportunity to know about proportion of each population yet.
2.2 Wholesale sellers
Wholesale sellers propose products that arrive every morning from their suppliers. They tend to prefer to sell products on the first day, mainly because most fruits and vegetables are highly perishable goods and would be less fresh the next day. Even for goods that could be kept from one day to another, the tendency of the wholesale sellers is to get rid of them as much as they can, since their storage ability are indeed quite low and limited by the market administrative organisation. One of their concern is to get rid of their goods in the best possible conditions, even on days when there is an abundance of them. A pool of regular buyers is then very advantageous for them, since they can rely on these transactions on any day.
Wholesale sellers depend on their own supplier to determine their prices, and know a bit about the average price of the market. They have two ways of negotiating with their suppliers, who can be either local producers or big companies who deal with national supply as well as importation. The first way is the buying principle: they get the good for a certain agreed value and pay the bill when they receive the product; the second way is called “after-sell pay” where they get a good in their store on behalf of a supplier, and when they have sold it, they announce the price they sold it to the supplier and keep 20% to themselves. This second method is much more interesting for the wholesale seller who can hide the real prices to the supplier, although he has to do it in a very discrete way. In our model, however, we will represent only the first method, where wholesale sellers have to buy products at a given fixed price.
All wholesale sellers are in competition with eachother. They usually know the prices of the other markets of the area and have an idea of the good price they should perform.
Hence, for both buyers and sellers, it is thus fundamental to maintain a network of relationships through day-to-day interactions on the market. However, one can see that a lot of retailers behave in a real rational way, trying to get as much information as they can so that to buy each product for the cheapest price.
2.3 Interactions and regular relations
The existence of regular relation is also at the origin of trust building and friendship apparition. Through their relations with wholesale sellers, retailers can get cheaper prices or information, come a bit later on the market and have some goods kept for them. On the other side, wholesale seller can make sure that they have regular demand. That’s why they tend to make cheaper prices to people who come and visit regularly. They also tend to make cheaper prices when retailers get a big “basket”, buying a lot of goods at the same time. It has to be stressed that on the market, quantities can vary in proportion from 1 to 10. The reduction that can be made go up to 20% of the price. On some very specific occasions, like when the products are getting old, people buying huge quantities can pay half price.
A further important factor applies to both buyers and sellers: they are human beings and since they spend a lot of their time on the market, a desire for friendship and fun is pursued as an end in itself (as well as cementing their economic networks). For those who can afford to delegate the installation of the shop, a significant part of their time is used for entertainment, either eating and drinking with friends, making jokes with their favourite sellers, and even playing games. In our first simulation set, we have had no opportunity to represent this dimension in the use of time, and focused primarily on the information gathering of the agents.
Two aspects interest us here: to focus on two dimensions of behaviour for the individuals: either having very regular interactions with few seller or using the market to get the best deals at any moment, using as many information as possible. This distinction is close to the one developed by (Galtier, 2002), who also stresses the possibility to develop two types of behaviours for traders: either they rely on network and trust the people with whom they interact, or they choose the best possible opportunities after taking as much information as possible.
We also want to represent the expectations of wholesale sellers, who react differently with agents depending on the regularity of relation and on the amount bought. This brings us back to the notion of norms, with expected behaviour that can be judge by both parties during the interaction, and where the meaning of each behaviour is socially known (Tuomela et al, 1995).
We attempted to reduce the motivation of the agent to a minimum: first getting all their product and then either getting the cheapest prices or relating to the same people as much as possible. Prices, as on the observed market, are considered as an external data, linked to the suppliers price policy, and not really on the market dynamics.
3 Model and simulations
3.1 Introduction to the model
In our system, there are two populations: wholesale sellers and retailers. At each time-step, retailers represent the demand and wholesale sellers provide the offer of products on the market. We represent a variation of supply on the market, with a constant demand. Prices are defined as an data that is mainly exogenous (the price that the wholesale sellers can get from their suppliers) and depends on a local adaptation that depend on the perceived demand and on the relation to a retailer.
From the field study that was performed, we developed two models of behaviour for agents: a “selfish” strategy that consists of the visiting of as many agents as possible so that to get the best prices or a “loyal” strategy where agents visit only one agent if they can.
What interests us in this work is to observe the influence of both rationalities in different context: when there is a huge diversity among sellers, in terms of prices or in terms of supply; on the opposite: when the market has homogenous characteristics; when there is a lot of variability between time-steps or when the market is stable. We observe data that we consider as representing the efficiency of the system: the fact that the retailers get the goods they need (relatively to the level of scarcity) and the waste that the
We characterise efficiency as the satisfaction of the needs of the agents (the products they require), the quality of the products that are sold (their age) and an estimation of who is advantaged by the prices of transactions. We have attempted to it keep this first simulation model as simple as possible without eliminating the phenomena of interest.
Aims:
Test the influence of the proportion of loyal agents and selfish agents in two context:
v when there is one time of arrival on the market or two periods for the agents to arrive
v when the supply varies a lot along the time, with big shortages or days with way too many products along the time, or on the opposite is quite stable
v when the number of products differs
v when the homogeneity of retailers is important or not
v when the homogeneity of wholesale seller is important or not
3.2 Agents and environment
Retailers
Retailers have to fulfil some needs at each time-step, that are given as five times one unit of product. The needs are randomly chosen at each time-step.
To achieve their goal of gathering the products, a retailer needs to go and visit wholesale sellers. The retailer has no representation of prices: it can compare the values among wholesale sellers, but doesn’t keep this knowledge from one time-step to another.
A retailer is characterised by two behavioural aspects: its degree of loyalty and the time it stays on the market. It can be either loyal or selfish, and the difference of behaviour which is implied will be described in the next section. It can stay for a short or a long time. There are 4 negotiation period on the market. A short-time retailer can stay for 3 periods; a long-time retailer can stay for 4 periods.
Retailers (mainly loyal ones) have a regular wholesale seller on the market, which is initialised randomly. For the first model, the regular wholesale seller is always the same along the simulation.
Retailers have to make choices about the wholesale sellers they want to visit and hence get information. This information gathering takes the same time as one negotiation period. Information that is provided concerns 5 randomly chosen wholesale sellers, and gives their current prices and availability of products.
When a retailer decides who it wants to visit, it send a message to the wholesale seller, proposing to buy a product. This message queues among other retailers’ and is answered to buy the wholesale seller. The retailer then knows if it has achieved its goal or if it has to stay on the market longer, if it can.
At the end of the day, it evaluates the quality of the transactions, scanning its memory of transactions it scans two types of information: for a loyal, a “good deal” is a deal where the whole request has been satisfied and a “bad deal” is when less than 50% of the request has been satisfied; for a selfish, a “good deal” is when the basket it bought was cheaper than the equivalent average basket on the market, by at least 20%, a “bad deal” is when it was more expensive by more than 20%. The information that is used as a reference is the average transaction price for each product, that is made public before the next period. From the accumulation of bad deals and good deals, agents build an image of the wholesale sellers. For the moment, it our model, we just observe what the images are, but we do not re-inject the results in the model.
Even if we have given the ability to evaluate to our agents, we don’t take this representation into account for the moment. We want at the next stage to have loyal retailers to be able to change their regular wholesale seller when it cannot provide them with goods on a regular basis, and selfish retailers to memorise bas deals they had.
Wholesale seller (goods, supply and prices)
Wholesale sellers have a certain quantity of each good that is displayed on the market. One unit of good is characterised by its date of arrival and its price. At the end of the 4. day after its arrival, the good is thrown away.
For each good, the wholesale sellers is characterised by a desirable stock: this is the number of each product it wants to have for one day. This number evolves in time: if the wholesale seller was found unable to provide this good, its desirable stock increases by 1 unit. If it has to throw away a good, it’s desirable stock decreases by ½ of the amount of the good thrown away.
The ability of the wholesale sellers to be supplied evolves from one day to another. Each day, each product is characterised by a probability of supply that is a characteristic of the environment. The wholesale seller makes a request to refill its stock to reach its desirable stock, and its chance to get its product is tested against the probability of supply. Either it gets all it wants, either its gets nothing.
The prices of all products evolve from one time-step to another, and are different for each wholesale sellers[4]. The prices evolution and initial diversity are limited by a percentage P and are such that:
- A initial general price is randomly chosen for each product, ranging from 50 to 100 per unit;
- The evolution of the general price stays in a range of P% more or less of the previous basic price;
- All agents get the product at a price that is randomly chosen in a range of P% more or less of that general price. It deduces the base price, by adding its own share
The price of units purchased by the wholesale seller can be different if it has bought them on different days. When required to give information about products, it gives the average base price The information it gives to circulate is the average price of that product in his stock. The heterogeneity of the prices for wholesale sellers are based on a double reality: they get their goods at different prices and they keep products that they acquired on different market days.
The way the wholesale seller sets the price of a deal is: when a retailer asks for a basket, the wholesale seller first calculates the price of the whole, using its base prices for each good. Then it sets the price according to the quantity bought and the relation to the agent:
If the agent takes a large basket (more than three units) it gets 10% off,
If the agent is identified as a regular, and takes less than 3 units, then it gets 10% off,
If the agent is identified as a regular, and takes more than 3 units, then it gets 20% off.
A retailer is regular if it asks for at least 20 % of its products to the wholesale seller (be the transaction agreed on or not) – meaning that its has made at least 10 requests in the last 10 days (memory length). The point of view of the wholesale seller on who is regular or not thus evolves in time. As seen previously, at initialisation a random wholesale seller is attributed to each retailer to be its regular. The initial set of regulars of the wholesale seller is made of all the retailers that consider it at their regular.
3.3 Time-step
A day is divided is 4 negotiation periods and individual calculating moments for the agents (see Table 1.). At one negotiation period, an retailer can either buy products or gather information. Selfish agents and loyal agents have different uses of time. As soon as an agent has acquired all its needs, or when its time is over, it leaves the market. Hence being short staying or long staying agent also has an influence on how they organise their time. Between interactions with retailers, a wholesale seller organises its supply and defines its prices.
Table
1: Here are the possible actions taken by the agents
along the 4 negotiation period and the calculus they perform in-between. L*
retailer is short for Loyal, S* for Selfish, *l for long-time, *s for
short-time. Long-time retailers have a different strategy for the last 2
periods. In bracket is given the number of wholesale seller the retailer is
going to visit at one negotiation period. Revisions for the wholesale sellers
are possible but not compulsory, and depends on cumulated demand.
|
Negot. Periods |
|
1 |
2 |
|
3 |
4 |
|
|
LS retailer |
|
Buy (1) |
Info Gath. |
|
Buy (1) |
|
Evaluates deals and
sellers |
|
Ll retailer |
|
Buy (1) |
Info Gath. |
|
Buy (1) |
Buy (1) |
Evaluates deals and
sellers |
|
Ss retailer |
|
Info Gath. |
Buy (1 to 5) |
|
Buy (1 to 5) |
|
|
|
Sl retailer |
|
Info Gath. |
Buy (1 to 5) |
|
Info Gath. |
Buy (1 to 5) |
|
|
Sellers |
Gets supply Calculates prices |
Answers requests |
Answers requests |
Revises prices |
Answers requests |
Answers requests |
Revises stock |
Supply and prices (wholesale sellers)
Gets supply: At the beginning of each time-step, a value is randomly chosen between supplyMin and supplyMax for each product. This value is the probability that a wholesale seller will get that product if it asks for it[5].
For each product, a wholesale seller knows how many units it needs to match its desirable supply. It then makes a request to the environment, which is satisfied or not, according to the probability for product. If the request is satisfied, the wholesale seller gets all the units it has asked for. Otherwise it gets none.
Revises stock: At the end of the time-step a wholesale seller throws away all goods that are older than 4 days in its stock. In that case, it changes its desirable supply by reducing the desirable quantity of that given product by 1. On the opposite, if it has been unable to provide this good during the time-step, it increases its desirable supply by 1.
Calculates prices: The price of each product is chosen randomly as described in the previous section. The wholesale seller elaborates its base prices for each product, by adding 30% to it.
Revises prices: The wholesale seller can revise its base price at half day: if it has sold less than 33 % at that time, it decreases the price by 10% ; if it has sold more than 66 %, it increases the price by 10%. As we shall see, the base price is not necessarily the one that is used to conclude deals.
Interactions: requests (retailers) and information
Buy: The agents make requests to wholesale sellers according to two different protocols, depending on their type.
v Loyal agents:
o At the first negotiation period, a loyal agent goes to visit its regular wholesale seller and asks him for the whole list it needs to gather; then if it is satisfied, it goes away, if not,
o At the second period, it gathers information on 5 wholesale sellers. This enables him to decide which agent can fulfil its needs the best,
o At the third period, it goes to time-step, it goes to this wholesale seller and asks it for all the remaining items. If satisfied or if it is a short-time retailer, it goes away.
o At the fourth period, long-time agents can go to a third wholesale seller to ask for the remaining products it needs.
v Selfish agents:
o A selfish agent spends the first negotiation period gathering information
o At the second time-step, it selects the cheapest wholesale seller he had information about
At the first negotiation period, a loyal agent goes to visit its regular wholesale seller and asks him for the whole list it needs to gather; then if it is
Information gathering
This activity takes one period of time for the agents. The information is made of five lists of prices, each of which being the base prices of a wholesale seller for the current period. If a wholesale seller is short of a product, then no price is associated to that product in the price vector. The sellers are chosen randomly for each retailer. five u=individuals made of five vectors of prices, representing the stock of five
Buying
For a loyal agent, Buying means to go and see one wholesale seller and ask to buy as many product as possible. For a Selfish agent, buying means to go to as many wholesale sellers as possible so that to get the best price on each product.
Information Gathering is an activity that enables the agents to know about the current stock of 5 randomly chosen wholesale sellers: the availability of the product and its price.
3.4 Buying interactions
The interactions that
take place between buyers and sellers are organised as asks and replies.
Wholesale seller’s point of view
First, a wholesale seller answers only for the goods it can provide at a given moment. It considers all its requests, ordering them on one principle: the regular agents come first, less well known agents come last. Among regular agents, he chooses randomly.
Two elements are important for the wholesale seller when it has to make decision over the price of a transaction: if the retailer is considered as regular ; the size of the basket it asks for.
Any retailer who asks for three units or more gets a 10% discount compared to the base price on the whole basket.
A regular retailer has two advantages: it has priority over the other buyers when several of them are in competition for the same unit of good ; it pays 10% less than the price it would have been proposed otherwise. A retailer is regarded as regular if it came to buy more than 20% of its stock in the last ten days (*memory length*), which means that it has asked for more than 10 products.
Retailer’s point of view
Retailers can have two different attitudes on the market, either be loyal or be selfish. One describes these two attitudes through the associated behaviour:
Loyal behaviour
1. On the first time-step a loyal retailer
goes to see its regular seller.
If it is satisfied (managed to get the whole list of products for its day),
it leaves the market.
2. If it is not satisfied, it gathers
information about who can provide him with the products it is looking for.
3. It chooses the wholesale seller who can
provide it with the more products (or chooses randomly among those that can
provide the major part of its needed products).
If satisfied or if it is a short
stay, it goes out of the market.
4. If not satisfied, It chooses the
wholesale seller which can provide it with the major part of its needs.
Selfish behaviour
1. On the first time-step a selfish
retailer gathers information.
2. From the 5 sets of prices it gets, it
selects the cheapest combination, and goes to all the related wholesale
sellers.
If it is satisfied, it leaves the market.
3. If it is not satisfied
if it is a short stay, it goes to a second best combination, and then
leaves the market, whatever the result.
if it is long stay, it gathers new information (updated in terms of availability and prices)
4. Chooses the best combination to go and
ask for the products he wants.
4 Simulations and results
The simulations are organised as a succession of time-steps, reported here as “days”. On each of these days, sellers refresh their stock by buying a number of each good they sell. The prices depend on how much the product costs them at this time step as well as the units they bought at the previous time-steps. Retailers are given a list of needs to supply. They can get information about the supply of each wholesale seller and of their prices, and depending on their strategy, they go and ask to the sellers for the goods they need. In the simulation described here, the memory is not integrated into the agents behaviour. For example, the seller that a loyal retailers considers as its regular seller does not change[6].
As stated previously, with our agent-based model, we examine the outcome
of simulations with different mixes of “loyal” and “selfish” buyer agents in
the market where supply is unpredictable with shortages and gluts. We examine
how loyal behaviour may help to smooth such irregular supply and produce a more
efficient market (in terms of the outcomes previously mentioned). We also
compare results when we change the market to remove unpredictable supply and
perishable products. The comparisons are based on three data: the satisfaction
of the needs of the retailers, the waste of products (thrown away after 4
time-steps) and the average time spent on the market.
Figure 1 shows a comparison of four kinds of market containing
homogenous agents of different types (Loyal agents with a long time on the
market (LL), Loyal agents with a short time on the market (LS), Selfish agents
with a long time on the market (SL) and Selfish agents with a short time on the
market. For each result (LL, LS, SL and SS) three statistics were collected:
The average number of unsatisfied agents after a market day, the average amount
of time spent by agents on the market and the average amount of products wasted
at the end of each market day. In all cases in figure 1 the results were
calculated by averaging these values over an entire run (of 200 market days)
and over 10 individual runs with different initial pseudorandom generator
seeds. Each population contained 100 retailer (buying) agents and 10 wholesaler
agents. There were 10 products in total with each agent having 5 randomly
chosen units of need (but each unit being for a different product). Other
values are as indicated in the previous text. Agents are considered to be
unsatisfied if they can not get all of their basket of products and have to
leave the market with some needs unfulfilled. The time statistic gives the
total units of agent time spent on the market per day (represented to 1/10th
scale on the figure).
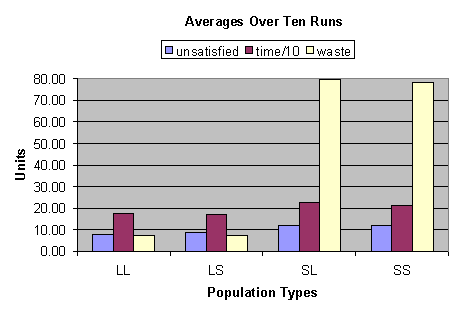
Figure 1. A Comparison of 4 different agent populations on the market. LL = Loyal agents, with a Long time on the market, LS = Loyal agents with a Short time on the market, SL = Selfish agents with a long time on the market, SS = Selfish Agents with a short time on the market. Waste = average units wasted (perished) products, time = average time spent on the market, Unsatisfied = average number of unsatisfied agents.
In figure 1 the major result is that waste increases significantly when
all the agents are selfish (SL and SS). You should also notice that both satisfaction
is increased and time is decreased when agents are loyal (LL and LS).
Figures 2, 3, 4 and 5 show typical individual runs for each of the four
population types. Notice that the “waste” statistic is represented as 5 times
scale in figures 2 and 3 but to scale in figures 4 and 5 (indicating how much
waste increases when the agents practice the selfish buying strategy).
There is a clue in the charts as to why waste goes so high for selfish
strategies. Notice that in the loyal populations figures 2 and 3 – there is
marked “ramp down” of the time and un-satisfaction values in the initial days.
This is due to the regular wholesalers learning the needs of their regular
customers and ordering reasonable amounts to satisfy those needs (remember that
wholesalers heuristically adapt their desirable stock levels based on waste and
unsatisfied orders). So when agents are loyal their regularly buying from a
single wholesaler allows that wholesaler to converge on a reasonable stock
level to smooth out erratic supply (even when prices vary between wholesalers).
However, in selfish populations (since prices vary and supply is erratic)
retailers (buyers) approach many wholesalers attempting to buy the cheapest
product. This stimulates wholesalers to keep stock to support these needs but
if prices are slightly higher than another wholesaler then stock gets wasted.
In a selfish market the wholesalers try to supply everything to everyone
meaning that the majority get undercut on any given market day by the lucky
wholesaler who got lucky with a low supply price. This same process makes
populations of loyal agents more likely to be satisfied.
Also selfish agents must spend at least 2 time units each on the market
(one to collect information and one to buy) making a total of 200 total units
per market day for all agents since there are 100 agents on the market. Loyal
agents may spend a minimum of just one unit each since they go straight to
their regular supplier (assuming that supplier satisfies all their needs).
Notice the time statistic does not fall below 100 in figures 2 and 3, and 200
in figures 4 and 5. Loyalty then, is a way of saving time.
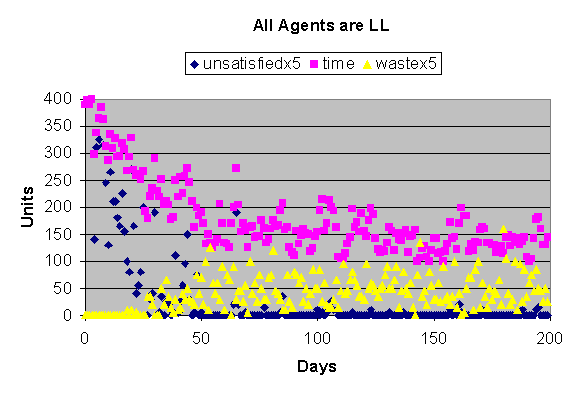
Figure 2. Results form an individual run for an LL population (loyal and
long time on the market). Notice the way the time and un-satisfaction falls as
the wholesalers adapt their desirable stock levels.
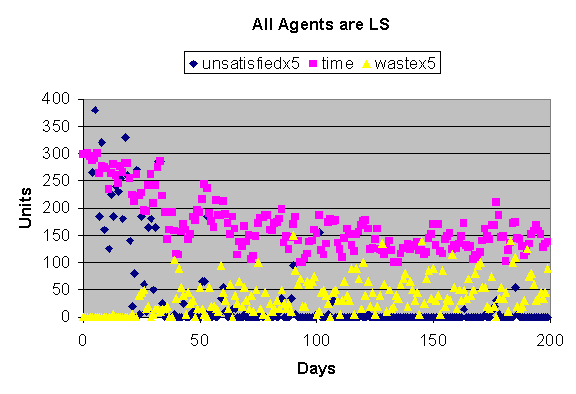
Figure 3. Results form an individual run for an LS population (loyal and
short time on the market). Notice the way the time and un-satisfaction falls as
the wholesalers adapt their desirable stock levels – as in figure 2.
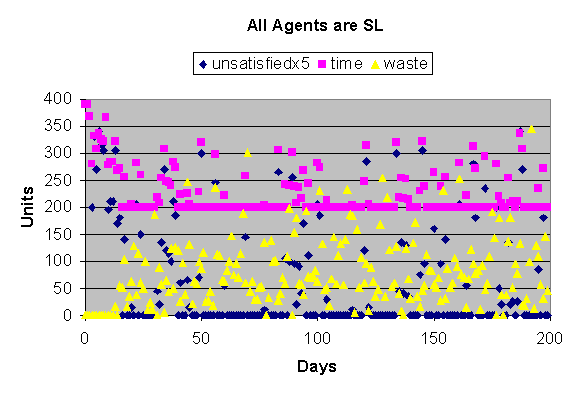
Figure 4. Results form an individual run for an SL population (selfish
and long time on the market). Notice that all values are much higher than the
previous figures (2 and 3). Specifically notice that the waste is now
represented to scale (rather than 5 times scale as previously in figures 2 and
3).
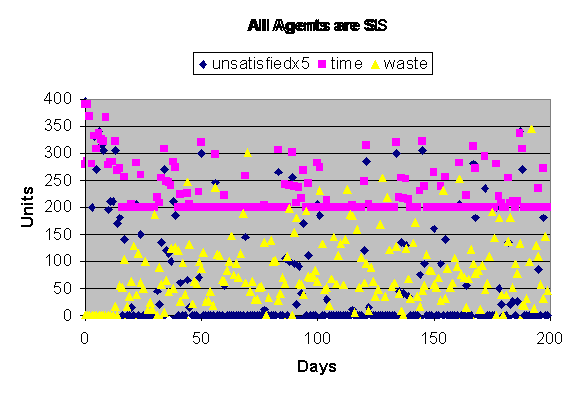
Figure 5. Results form an individual run for an SS population (selfish
and short time on the market). We can make similar observations to figure 4.
5. Conclusions and Future Work
Our general conclusion is that in this simplified “pilot” model, we find that a high level of loyalty in the market tends to produce a more “efficient” market where all benefit and share the costs of risk and uncertainty when unpredictability of supply and potential loses are high. We speculate (and will produce further experiments to test that) loyalty is less important when supply is constant and potential loses low.
Our insights with this current (first draft) simulation are not “earth-shattering”. Indeed more work will be required to relate the model back to real phenomena. It would seem that (in this model) the way that wholesalers modify their desirable stock levels is very important and we need to look back at the real world market to explore this in more detail. Also, our insight that processes other than price mechanisms may help to stabilise or “lock-in” market behaviour in the form of a kind of self-organising complex system is not new (Moss 1980).
Currently our model of this negotiation process is limited, in relation
to the real phenomena. A slightly more accurate communication process will be
organised in the next step, with the buyer being able to reformulate the offer
to make it more desirable and communicate that back to the seller who in-turn
might modify the offer.
Also we currently do not relate price to shortages or to sales by the
retailers – we simply assume that retailers dispose of all their products
without reference to price. We therefore (if could be argued) underplay price.
However, we intend to include this in later versions.
Finally we need to address the integral aspect of “fun” on the market.
Our initial intention was to explicitly model this as a need – it was observed
that as human beings who are spending a good part of their lives on the market
the traders enjoy social aspects of their relationships and pursue these
aspects as a goal also (in addition to the trade element). The two aspects are
rarely opposed – i.e. going to the “bar” on the market is a time to socialise
with friends but also to follow up prices on the market and spread information
of “good deals” and anecdotes concerning “bad guys” etc. We believe our model
will be a basis to build on such social relations in future – then we can finally
explore “fun”. The fun is yet to come.
We will continue to develop the model. A further step will also allow
for the involvement actors in the evaluation of the model such that they can
informally validate it and perhaps pose questions and hypotheses of their own.
Acknowledgements
We thank CNRS and British Council for supporting the collaborative research program between CPM and GREQAM
References
Barreteau, O. and Bousquet, F., 2000, SHADOC: A Multi-Agent Model to tackle viability of irrigated systems. Annals of Operations Research, 94, 139-162.
Bousquet François, Barreteau Olivier, Mullon Christian and Weber Jacques, 1999, An Environmental Modelling Approach. The Use of Multi-Agents Simulations, In: F. Blasco and A. Weill, Advances in Environmental and Ecological Modelling}, pp 113-122.
Chiarella Carl, Dieci Roberto and Gardini Laura, 2002, Speculative Behaviour and Complex Asset Price Dynamics: A Global Analysis, Journal of Economic Behaviour and Organization, vol 49, pp 173-197.
Galtier Franck,
Bousquet François, Antona Martine and Bommel Pierre, 2002, Les Marchés Comme
Systèmes de Communication. Une évaluation de la performance de Différentes
Institutions de Marché à l'aide de simulations informatiques, In :
Proceedings of Les Systèmes Agro-Alimentaires Localisés (Syal), CIRAD,
Montpellier, France.
Janssen Marco A. and Jager Wander, 2001, Fashion, Habits and Changing Preferences: Simulations of Psychological Factors Affecting Market Dynamics, Journal of Economic Psychology, vol 22, pp 745-772.
Kirman, Alan, 1995, Learning in oligopoly, Theory, simulation and experimental evidence, In: Kirman A. and Salmon M., Learning and rationality in economics, p127-150.
Kirman, Alan, 2001, Some Problems and Perspectives in Economic Theory, In: Debreu G., Neuefeind W. and Trockel W., Economic Essays, A Festschrift for Werner Hildenbrand, pp 231-252, Springer, Berlin.
Malinowski Bronislaw,1922, Argonauts of the Western Pacific : An Account of Native Enterprise and Adventure, Routledge & Kegan Paul, London.
Moss, Scott, An Economic Theory of Business Strategy Oxford: Basil Blackwell,1980.
Rabin Matthew, 2002, A perspective on psychology and economics, European Economics Review, vol 46, pp 657-685.
Rouchier, J.,
Barreteau, O. and Bousquet, F., 1998, Evolution and Coevolution of Individuals
and Groups, In: Yves Demazeau (Ed), Proceedings of the Third International
Conference on Multi-Agent Systems, IEEE, Los Alamitos, USA, pp 254-260.
Smith Vernon, 2002, Method in Experiment: Rhetoric and Reality, Experimental economics, vol 5, pp 91-110;
Tarrius Alain,
2002, La mondialisation par le bas. Les nouveaux nomades de l’économie
souterraine, Balland, Paris.
Tesfatsion Leigh, 2002, Agent-Based Computational Economics: Growing Economies from the Bottom Up, ISU Economics Working Paper No. 1 15 March 2002 http://www.econ.iastate.edu/tesfatsi/ .
Tuomela Raimo and Bonnevier-Tuomela Maj, 1995, Norms and Agreement, European Journal of law, philosophy and computer science, vol 5, pp 41-46.