Linking multi-agent simulation to experimental economics: problems, interest and issues that appear through re-implementing John Duffy’s model of speculative learning agents
1 GREQAM, CNRS, 2 rue de la Charité,
13002 Marseille, France
rouchier@ehess.cnrs-mrs.fr
Abstract. The paper presents an attempt at
replication of a multi-agent model dealing with the issue of speculation. In
the Journal of Economic Dynamics and Control, John Duffy presents his model and
results, as a coupling between an experimental economic version and a
multi-agent version, of a model by Kiyotaki and Wright (1989). This original
model offers a structural setting on which to base a microeconomic view of
speculation, by designing a production-exchange-consumption setting with three
goods that differ by their storage costs. Here, I present my own version of the
multi-agent model, which is as close as possible to John Duffy’s, although I
have been unable to reproduce his actual results. Most of my results are neither
close to the experimental data or the simulation data, which makes me discuss
the model of rationality of agents itself, and the way the results were
described. The replication process is all the more interesting that it allows
to redefine the relevant indicators to analyze the model.
Key words : multi-agent simulation, experimental economics, speculation, learning, model validation
Résumé. Cet article présente une tentative de réplication d’un modèle agent sur le thème de la spéculation. John Duffy présente son modèle et ses résultats dans le Journal of Economic Dynamics and Control : il s’agit d’un travail de couplage entre économie expérimentale et simulation agents, qui s’inspire du modèle de Kiyotaki et Wright (1989). Le modèle original offre un environnement structurel pour baser les comportements micro-économiques d’agents effectuant des spéculations. On y trouve ainsi une définition de dynamiques de production-échange-consommation autour de trois biens qui diffèrent simplement en termes de coût de stockage. Ici je présente ma propre version du modèle, aussi proche que possible de celle de Duffy, même si je n’ai pas été capable de reproduire ses résultats de simulation. Mes propres résultats ne sont proches ni des données expérimentales, ni des données issues des simulations, ce qui m’amène à critiquer le modèle d’apprentissage lui-même, mais aussi la façon dont les résultats sont transmis dans l’article d’origine. Le processus de réplication est d’autant plus intéressant qu’il permet de redéfinir les indicateurs les plus pertinents à l’analyse du modèle.
Mots clefs :
simulation multi-agent, économie expérimentale, spéculation, apprentissage,
validation de modèles
JEL : B59, C89,
C99, G00.
1. Introduction
In this paper, I describe the re-implementation of the model of a society based on the construction of an artificial market where speculative behaviour are due to appear. The paper that influenced this work is a 2001 paper, published by John Duffy in the Journal of Economic Dynamics and Control in which he uses a comparison between results that he got by performing simulations and those in an equivalent setting where he organised experiments with real humans. The model on which his own research is based is a model that was designed in 1989, by Kiyotaki and Wright, in a classical economics paper. These two economists wanted to find out the institutional setting that would induce people to display some speculative strategies, and maybe understand the emergence of money through this mean. Their model has then been re-used by various authors, some of whom have elaborated an agent-based approach on it (Basci, 1999), some others who have performed experiments with humans (Duffy and Ochs, 1999a). I will thus report here the theoretical setting and the work of Duffy whose aim was to link both experimental and simulation results. His research is part of a growing trend in experimental economics, where researchers tend to make simulation with artificial agents to check their assumptions on rationality (Meidinger, ).
I then will describe the problems that arose while re-implementing the model. They led me to spot one element that was unclear to me regarding the choice of cognitive processes for the agents. I will first describe the model that was established by Kiyotaki and Wright when they wanted to create an institution to induce agents to speculation. Then I will describe the agent-based model that Duffy made with this setting, studying the rationality of agents with bounded rationality, eventually I will explain the difficulties I had in reproducing the same results as Duffy had found.
Duffy’s aim was to compare simulations’ results with experimental data and I was unable to reproduce the same results. This fact made me consider the link between both techniques as a new tool that should be globally conceived. The type of research that is led in experimental economics is still based on different issues than the one of “artificial economics”, still closer to Artificial Intelligence, and linking both tools forces to drastic choices in the exploration of possible settings. I will discuss the type of comparison he has established in his paper and advocate for another way of capturing cognitive processes so that to better explore the actual learning techniques of humans[1]. To me, only the micro behaviour comparison can spread some reciprocal lights on the practices. Modeling the European regulation for GMO release.
2. A model of market to induce speculative attitudes
2.1. A three goods model
Kiyotaki and Wright in their paper (Kiyotaki and Wright, 1989), define a market in which three different types of agents perform decentralised bilateral negotiations[2] concerning three different goods, called good 1, good 2 and good 3. The agents need to consume a unit of good to increase their utility[3] and they produce a unit of good each time they have consumed one: an agent 1 needs good 1 and produces good 2; an agent 2 consumes good 2 and produces good 3; an agent 3 consumes good 3 and produces good1. To make it easier, Kiyotaki and Wright write that agent i consumes good i and produces good i+1. As one can note: agent necessarily exchange when they want to consume and not all agents can be satisfied by just one exchange. Indeed if two agents exchange their own production goods, one can be satisfied but the other would get a useless good, good i +2 which is neither its own production good nor its consumption good. The constraint of the bilateral trading creates a compulsory conservation of goods from one time-step to another. An agent who exchanges and stores i+2 is speculating, since it speculates on the gain it will have at the next time-step, when it might get its consumption good through exchange[4].
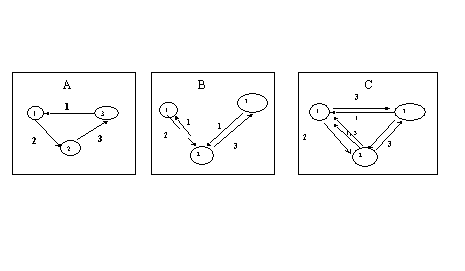
Figure 1 : A) From producer to consumer: the ideal circulation of goods (impossible to achieve on this market which rule is bilateral trading) ; B) Fundamental strategies in the context of the model (neither agents 1 or 3 is interested in trading for the good i +2 ; C) Speculative equilibrium pattern, achieved for certain values of costs.
To keep each good from one time-step to the other, there is a storage cost, c1, c2 and c3. They are not equal, hence are agents not symmetrical : 0 < c1 < c2 < c3 < u, where u is the utility gained for the consumption of one unit. Each agent can keep only one unit and those units cannot be divided. An agent will never store its own consumption good: at one time-step, if it gets its good through exchange, it consumes it and produces his production good right away, which is stored until next time-step. To have some risk associated to the conservation of units of good, and to increase the decay of the value of each good, a discount factor is introduced: at the end of each time-step, to decide if the markets shuts or continues, a number is randomly chosen and compared to this discount factor β (0 < β < 1).
2.2. Diverse optimal behaviours
Obviously, since not all conservation costs are alike, the interest of exchanging goods will be different for the three types of agents.
One can note
γ (i+1) = - C(i+1) + βu, (1.1)
the expected gain for an agent who keeps good i+1 and sells it at the next time-step ; and
γ ( i+2) = - C(i+2) + βu, (1.2)
the same gain for good i+2.
The only agents who are interested in exchanging their production good i+1 for i +2 are agents of type 2: the cost of keeping good 1 is lower than the cost of keeping their production good, 3. In this case, their fundamental strategy, with short term perspective, is equivalent to speculation. For the others, the fundamental strategy is to keep their production good, which storage cost is lower. However, even agents 1 and 3 can be interested in performing speculation: at each time-step, the gain they can expect at the next time-step depends on the fact that they will meet an agent willing to trade and to give them their consumption good.
One denotes pi the proportion of agents i that possess the good they produced (i+1) at a given time-step, and (1-pi) the proportion of agents i who have traded this good for good i+2. Kiyotaki and Wright demonstrate that, knowing p1, p2 and p3, it is possible for agents 1 and 3 to decide if they will speculate or not. Actually, the result is such that it is possible to find values of storage costs and of repartition of goods in the market, for which agents 1’s best strategy is to speculate any time it is offered to them, and agents 3 to never speculate. The other situation is the one that corresponds only to fundamental strategies, and to have only agents 2 speculate. These two situations can be read in the Figure 1 which represents possible exchanges at each time-step, any other exchange being rejected by one of the agent. Figure 1B is the case where only agents 2 speculate and Figure 1C is when both 1 and 2 accept to speculate.
One can denote Si the optimal strategy of an agent i at one time-step, where Si = 1 if i accepts to exchange and Si = 0 if it refuses. One then writes the situation of a society as (S1, S2, S3), which gives a complete description of the strategies of the agents. In the centralised approach of Kiyotaki and Wright where all agents have the same knowledge, at a given time-step, all agents of the same type will make the same choice.
In some settings, agents of type 1 can be interested in speculating. For the other two types of agent, there is no other behaviour to choose than what is called their “fundamental” strategy, where agents 2 speculate and agents 3 don’t, whatever the parameters in the system. In this system, the central issue is thus the speculative attitude of agent 1. The behaviours in the society can be represented by two different vectors, depending on whether the agents of type 1 do speculate or not: s = (1,1,0) or (0,1,0).
This environment, made of a production-consumption dynamics and an exchange institution, was designed by Kiyotaki and Wright to induce agents to use one of the goods as an exchange good. In the model, an agent can decide to perform an exchange to get a good which it does not consume, and this is what is called to “speculate”. Considering the storage costs, only agents 2 speculate at any time ; agents 3 never speculate ; agents 1 can speculate for some values of β and of p1, p2 and p3. To decide if it can speculate, the agent needs to have complete knowledge of the situation of all other agents: their type and what they possess. This last assumption is the one that both the experimental approach and the multi-agent approach want to release. The interest for these two approaches is to understand which type of information can be used by agents that are independent, whose sole common knowledge is the set of rules of the system and only learn through their interactions with the others. To decide to speculate or not, agents cannot decide for an optimal behaviour, they will have to acquire information of which situation is the best for them. In the following section is described the experiments that were led to check the ability of humans to evolve in such an environment: some indicators are chosen to show the evolution of their behaviour.
3. Learning through experience
3.1. Experimental data
A few studies were led by experimental economists to explore the possible behaviour that humans would display in such an environment as reported in Brown (1996)). The first work of Duffy on that topic (Duffy and Ochs, 1999) consist in a set of controlled laboratory experiments with humans who are confronted to a market setting where they have to make choices. To re-create the Kiyotaki-Wright environment, each participant is assigned a type, either 1, 2 or 3, and given all information about the rules of utility earning, storage costs and decay value in the context of production, exchange and consumption which is organised. At each time-step participants are randomly matched with another agent from whom they know nothing but the good that he or she possesses and if he or she is willing to exchange for his own good. Experiments were led 10 in a row, with a decay value of 0.9, and hence there were about 100 exchange opportunities for each session.
What Duffy observes in each session is the tendency for each type of agent to speculate. The tendency is represented by the ratio: (number of accepted trade implying speculation) / (opportunity to trade implying speculation). For example, a participant of type 1 is said to accept an exchange for speculation if he/she proposes to give good 2 to get good 3. In the experiments, participants do learn what is their best attitude while playing, and we assume their behaviour thus evolves towards what they think the best choices. To take this learning into account, Duffy compares the average ratio of speculation tendency for all the agents of the same type over the first half of the session and over the last half of the session.
Table 1: Offer frequencies over each half of 5 sessions with real agents.
|
|
Agents type 1 offers 2 for 3
|
Agents type 2 offers 3 for 1
|
Agents type 3 offers 1 for 2
|
|||
|
|
first half of the experiment |
second half of the experiment |
first half of the experiment |
second half of the experiment |
first half of the experiment |
second half of the experiment |
|
R1 |
0.13 |
0.18 |
0.98 |
0.97 |
0.29 |
0.29 |
|
R2 |
0.38 |
0.65 |
0.95 |
0.95 |
0.17 |
0.14 |
|
R3 |
0.48 |
0.57 |
0.96 |
1.00 |
0.13 |
0.14 |
|
R4 |
0.08 |
0.24 |
0.92 |
0.98 |
0.12 |
0.02 |
|
R5 |
0.06 |
0.32 |
0.93 |
0.97 |
0.25 |
0.18 |
|
Average on R1-R5 |
0.23 |
0.37 |
0.95 |
0.96 |
0.20 |
0.16 |
In this experiments, the parameters are such that agents of type 1 should discover along the time that their best strategy is to speculate, the same being true for type 2 agents and type 3 being induced to refuse speculation when they meet this opportunity. What Duffy hence shows is that humans who are engaged is the game are not learning to get to the optimal rationality. This is especially true for agents of type 1.
To try to induce participants to speculate more and thus have the system attain the equilibrium earlier, Duffy introduces two new settings for his experiments. First, he decides to change the number of each agent for one type. By this mean, some of the meetings would occur more often and hopefully help agents of type 1 learn quicker that they have to speculate. Hence, the repartition of participants would be such that 1/3 of the agents being of type 1, less than 1/3 being of type 2 and more than 1/3 of type 3 : with 18 agents all together, meaning 6, 4 and 8. The other option to test the ability to learn of participants of type 1 is to mix them with automated agents that always follow their fundamental strategy (agents of type 2 always accept to speculate and agents of type 3 always refuse to). Human participants are all of type 1, are aware of who they are mixed with and they have to choose between speculating or not when they face the opportunity. Table 2 shows that the speculative attitude of the agents in this last case is more general and is quite stable over the experiment: Duffy’s conclusion is that this second setting is the one that induces agents to speculate in the best way.
Table 2: Offer frequencies over each half of 5 sessions with real agents mixed with automated artificial agents.
|
|
Agents type 1
|
Agents type 2
|
Agents type 3
|
|||
|
|
Time-step for the first half |
Time-step for the second half |
Time-step for the first half |
Time-step for the second half |
Time-step for the first half |
Time-step for the second half |
|
R1 |
0.84 |
0.83 |
1.00 |
1.00 |
0.00 |
0.00 |
|
R2 |
0.52 |
0.53 |
1.00 |
1.00 |
0.00 |
0.00 |
|
Average on two sessions |
0.69 |
0.71 |
1.00 |
1.00 |
0.00 |
0.00 |
3.2. Decentralised model
What mostly interests Agent-Based modellers is the building of a society with decentralised knowledge. Agents that are used are autonomous, usually have no global knowledge of their society and thus cannot calculate the optimal action to undertake. If a globally optimal situation exists, the issue that pushes to the building of artificial society is to understand what individual learning processes could lead the group to attain that equilibrium.
This point of view is quite close to the research led by experimental economists and their observation of actual circulation of information and actions. In the simulations that were already led to explore the Kiyotaki-Wright environment, researchers developed some learning algorithms and observed the apparition of speculative behaviours for the agents in societies with a big number of interacting agents (Marimon, McGrattan and Sargent, 1990 ; Basci, 1999; Staudinger , 1998). To study the evolution of speculation in the group, Duffy chooses to build agents that are not able to calculate their optimal strategy: they have no more information than their past interactions with others, not even knowing that there exists other types of agents, different rationalities or ignoring the repartition of goods in their environment. More specifically, in this paper, Duffy built an artificial society that would be as close as possible to the real experimental settings he had made, to make sure he could actually compare his agents’ actions to humans’ behaviour in the same environment. He takes a small number of agents (maximum 24) and makes short simulations. Here is described the rationality that Duffy then builds in for his agents.
Of course, artificial agents cannot be said to be aware of the setting in which they are evolving, but the calculus that they perform aggregate the data that human subjects are given: one can refer to equation 1.1 and 1.2 for the definition of expected gains, where the decay factor and the storage costs are used. Choices for agents are defined such that:
– if an agent meets another agent who owns the same good as his, none of them proposes the exchange.
– If an agent meets an agent who possesses its consumption good, then it necessarily proposes the exchange
–
In any other case, which means if the
agent can trade good (i+1) for good (i+2) or the opposite, it depends on its
past successes in getting good i:
One defines:
ν i+1 = Σ (IS i+1) * γi +1 - Σ (IF i+1) * γi +2 (2.1)
ν i+2 = Σ (IS i+2) * γi +2 - Σ (IF i+2) * γi +1 (2.2)
where both (I i+1) are functions which are defined on the set of time-step when the agent possessed good i+1 and:
IS = 1 if the agent traded i+1 for i; and = 0
if it didn’t.
IF = 1 if
the agent failed to trade i+1 for i; and = 0 otherwise.
With the same
definition for both (I i+2).
When the agent j, of
type i faces the opportunity to speculate (hence to exchange (i+1) for (i+2))
then one defines:
xji = νj i+1 - νj i+2
(3)
and:
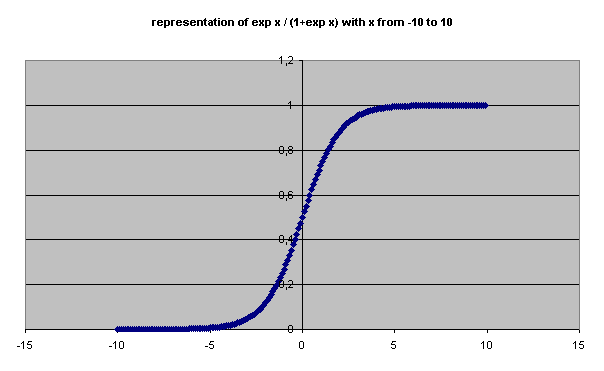
P [s=0] = exp xji / (1 + exp xji) (4)
is the probability
for the agent to reject the exchange.
Eventually:
P [s=1] = 1 - P [s=0] (5)
is the probability
for the agent to accept the exchange. In the appendix, there is a
representation of the function exp x / (1 + exp x) that can help visualize the
reason why such a function is chosen to be
With this decision process, only its past actions are used by the agent to make a choice, with no necessary knowledge of an optimal decision that could be taken. From the paper of Kiyotaki and Wright, one can choose the values of c1, c2, c3, so that to expect that for certain values of agents of type 1 will learn how to speculate, although it wouldn’t be their optimal short-term decision. The use of probabilities is necessary in the choice process to make have agents start and try speculating. They will increase the probability to do it again if the result of this action proves to be successful (i.e.: if they are not stuck with good i+2 for a too long period, unable to exchange it for good i).
3.3. Reproducing the model
The main elements of the model were extremely clear in the paper, and very straightforward to reproduce[5].
However I found two small ambiguities in the whole building. For both of them, the actual choice made by John Duffy is very logical and direct, but since the choice is not mentioned in the paper, and considering my wish to reproduce his system very precisely, I couldn’t make the decision myself. The resolution was quick: I asked him via email, and he answered the next day, for both questions. As will be mentioned later, there was also an issue in the interpretation of observation indicators, and again I checked with him and he was extremely diligent in his answer. This communication was very important in my understanding of the whole work performed. I haven’t asked him for his actual code for two reasons: I wanted to reproduce the results with my own platform (which is for me the most important: to test the transmission of model via natural language, like in journal papers) and I wasn’t sure I would be able to read his own code anyway.
The two questions I asked were:
o it is not said in the paper if there is a possibility for agents to choose to exchange good i +2 for good i+1. Maybe agents who speculate would never go back to possessing the good they have produced. Although I would have thought that the process described in (3) and (4) would be symmetrical, I asked the original author. The answer is that, facing the opportunity to exchange good i+2 for i +1, the process is the same as in the other case, and agents calculate the value of
y = ν i+2 - ν i+1 (3 bis)
to use probability:
P [s=0] = exp y/ (1 +
exp y)
(4 bis)
Hence the choice procedure is with no memory regarding the way this good has been obtained and the agent can
o the value of IF (i+1) is defined as the fact that the agent failed to trade i+1 for i, but it is not said what is counted as such a moment: is it “any time the agent could have traded, proposed, and was rejected” (meaning any moment when it meets another agent who possesses i but refuses to trade) or is it “any round that the agent starts with possessing i+1 and ends without possessing i” ? It does make a substantial difference, when it comes to the probabilities we have. The answer is that agents use “the "larger set" interpretation: they count the number of periods in which they were holding i + 1 but could not trade for i, regardless of which good they are matched with” (John Duffy, personal communication), and they compare with the same result with i +2.
In the simulation that Duffy presents, he says that sometimes agents do act according to the above logic, sometimes they act in an automated way, systematically rejecting or accepting to trade. Since the system was originally design to make agents of type 1 speculate, they are the only ones who always follow the learning rationality. For the others, as we saw, the dominant strategy is such that:
- agents of type 2 always accept to get good 1 in exchange of good 3,
- agents of type 3 always reject to get good 2 in exchange of good 1.
In the simulation protocol, when the agents use this last way of choosing, they will be referred to as “automated agents”, whereas they will be called “rational agents” if they learn.
The system I designed does match the above model. However, since I have had problems in finding the same results as John Duffy in my simulations, before I got in touch with him I could imagine two other algorithms just by reading his paper, and tried these two variations. Both logics correspond to the questions cited above. The changes are made in an independent ways, never occurring at the same time in one simulation.
o The first change is that I do not allow agents to exchange good i +2 for good i + 1: once they have speculated they have to keep to their choice and see the result of that action. I call these agents “stable-rational agents”. In that case, agents never exchange to get the good they produce.
o The second change is changing the meaning of If (i+1) and using the “narrow” definition of If (i+1), which I call Jf (i+1) and Jf (i+1). Then: Jf (i+1) = 1 if and only if an agent had the opportunity to trade i+1 for i, but the other agent rejected the offer. For me the idea was that the agent could thus infer that if it had possessed the other good, the other agent would have accepted to trade. I call them “var-rational agents” in this case.
Table 3: the names and repartition of rationality for the agents, depending on their rationality. Agents in italic letters are the one that are used by John Duffy in his simulations
|
Name of the agent |
Agents of type 1 |
Agents of type 2 |
Agents of type 3 |
|
Rational agents |
Compare I(2) and I(3) |
Compare I(3) and I(1) |
Compare I(1) and I(2) |
|
Stable rational agents |
Never exchange 3 for 2 |
Never exchange 1 for 3 |
Never exchange 2 for 1 |
|
Var-rational agents |
Compare J(2) and J(3) |
Compare J(3) and J(1) |
Compare J(1) and J(2) |
|
Automated agents |
Compare I(2) and I(3) |
Always exchange 3 for
1 |
Never exchange 1 for 2 |
4. Simulations and results
4.1. Different simulations
Before describing the simulation protocol, it is interesting to recall why Duffy designs his model. He finds it quite difficult to observe speculative behaviours among human participants of type 1, although speculation should be the dominant strategy for agents 1 and 2. He thus wanted to understand what would be a good description of the rationality at stake. That’s why it was interesting for him to model a given logic into his agents and test the type of behaviour it would globally create. The different constraints he puts in the organisation of the model are also copied from his experimental research. To make sure he could compare the results, he decided to build societies that were exactly of the same size as in his experimental protocols. It seems indeed intuitively logic that there should be some special attention given to the scale of society in a society where random meetings are so important.
His simulations are run during 10 games. Each game is a succession of time-step, during which agents are pair randomly once and decide to exchange or not. The discount factor he choose is 0,9 (hence, on average, there are 100 time-steps of possible exchanges). At the end of one game, agents get back to the origin of game where they possess their production good, and they are not able to get rid of the good they have at the previous time-step.
For John Duffy there are 3 different simulations, with different rationality and repartition of agents, copied from his experiments:
o simulations with 8 agents of each type, all behaving in a rational way,
o simulations with 1/3 of agents of type 1, but less than 1/3 of type 2 and more than 1/3 of type 3. He run his tests with 18 agents all together, meaning 6, 4 and 8.
o Simulations with 8 agents of each type, but only the agents 1 being rational, and all other agents being “automated”: agents 2 always accept to speculate, agents 3 always reject.
For each simulation he looked at two kinds of data and compared them with the ones acquired by running experiences with real subjects:
o The average “frequency of speculation” for each type of agents over the first half and the second half of the simulation, which means :
·
if: Ai = number of times a speculation
is possible and accepted by one of the agents of type i (be it accepted by the
other or not)
·
and: Ri = number of times a
speculation is possible and rejected by one of the agents of type i (be it
accepted by the other or not)
· then :
Fi = Ai / number of possibilities to speculate = Ai/ (Ri+Ai) (5)
o The actions chosen over time by each agent i who faces the opportunity to trade Good i+1 for Good i+2, which is then represented by a series of –1 and 1, where –1 is for a rejection and 1 is for an acceptance.
To perform my own research, I didn’t have access to any data related to real experiments, and I established relations only between John Duffy’s results in artificial societies and mine. I didn’t try to study the case where agents are all rational but with different number of each type, but reproduced both the other protocols. Indeed, the reproduction of this system was mainly a benchmark to me, to make sure that I would attain the quick convergence that Duffy observes. First, when I was running my simulations, almost all results were different from his. Before I got in touch with him to know if my algorithm was right, I enriched the number of possible behaviours to try to reach his results:
o Simulations with agents being all “stable-rational” (once they start speculating with one unit of good, they don’t exchange it until they can get their consumption good)
o Simulations with agents being all “var-rational” (where the comparison of possessing good i+2 instead of i+1 is based on the narrow set described above).
Then, to test the efficiency of the
learning processes in situations that were more constrained, I haven’t done the
same simulations as Duffy with different number of agents in each category, but
I have used the mixing possibilities, mixing rational agents (with my three
types of rationality) and automated agents and thus performing simulations
where agents of type 2 and 3 are automated.
One can summarize:
Table 4: simulations that were led. The series of simulations reproducing Duffy’s are indicated in italic, and the ones I added are in normal format
|
|
Rational agents |
Stable rational agents |
Var-rational agents |
|
Homogenous rationality |
SIM 1 Duffy: 5
simulations Me: Average and MSD over 100 simulations |
SIM 2 Average and MSD over 100 simulations |
SIM 3 Average and MSD over 100 simulations |
|
Heterogenous rationality |
Series of 5 simulations SIM 1 – 23 Agents of type 2 and 3 are automated – |
Series of 100 simulations SIM 2 – 23 Agents of type 2 and 3 are automated – |
Series of 100 simulations SIM 3 – 23 Agents of type 2 and 3 are automated – |
4.2. Results and comparisons
The results of my simulations are quite different from John Duffy’s, whatever the type of rationality I put in my agents. Here, I wont’ give 5 results of simulations, but the average result and the medium square deviation for 100 simulations in a row.
I first checked step by step the simulation results to make sure that no mistakes were introduced in the setting or in the learning algorithm, but I couldn’t detect any difference between what the system is supposed to do and what it actually does. I have a high confidence in the adequacy between what is expected from the code and what it actually does, although this verification process has only been carried by hand, and not with a special programming tool[6]. The results are shown in the following tables.
Table 5: Duffy’s results for each of 5 artificial sessions, average for these 5 sessions. Frequency of speculation offers for each type of agents
|
|
Agents
type 1
|
Agents
type 2
|
Agents
type 3
|
|||
|
|
Time-step for the first half |
Time-step for the second half |
Time-step for the first half |
Time-step for the second half |
Time-step for the first half |
Time-step for the second half |
|
A1 |
0,06 |
0,15 |
0,73 |
1,00 |
0,37 |
0,07 |
|
A2 |
0,23 |
0,31 |
0,88 |
0,98 |
0,20 |
0,07 |
|
A3 |
0,33 |
0,50 |
0,78 |
0,98 |
0,15 |
0,00 |
|
A4 |
0,18 |
0,42 |
0,81 |
1,00 |
0,17 |
0,00 |
|
A5 |
0,10 |
0,18 |
0,67 |
0,98 |
0,23 |
0,07 |
|
Average on A1-A5 |
0,19 |
0,32 |
0,77 |
0,99 |
0,22 |
0,04 |
Table 6: My results for simulations of all types with homogenous agents that are either: rational agents, var-rational agents and stable agents. I ran 100 simulations, among which some results were not suitable because the time of simulation was too short and agents did not have the opportunity to speculate. Then I took the average and MSD over the remaining simulations (over 90) of the speculation rate for each half of simulation for each t type of agents.
|
|
|
Agents
type 1
|
Agents
type 2
|
Agents
type 3
|
|||
|
|
|
Time-step for the first half |
Time-step for the second half |
Time-step for the first half |
Time-step for the second half |
Time-step for the first half |
Time-step for the second half |
|
SIM 1 Rational agents |
Average
speculation rate |
0.74 |
0.68 |
0.80 |
0.93 |
0.73 |
0.81 |
|
MSD |
0.03 |
0.10 |
0.08 |
0.09 |
0.01 |
0.11 |
|
|
|
|
|
|
|
|
|
|
|
SIM 2 var-rational agents |
Average
speculation rate |
0.45 |
0.42 |
0.53 |
0.47 |
0.42 |
0.52 |
|
MSD |
0.19 |
0.27 |
0.14 |
0.27 |
0.3 |
0.24 |
|
|
|
|
|
|
|
|
|
|
|
SIM 3 Stable agents |
Average
speculation rate |
0.68 |
0.77 |
0.76 |
0.79 |
0.66 |
0.66 |
|
MSD |
0.07 |
0.12 |
0.01 |
0.09 |
0.04 |
0.12 |
|
The results that I get in my simulations are all very interesting, but can unfortunately not be thought of as being similar to Duffy’s. At first it was a bit of a problem since I didn’t know which precise algorithm to reproduce and none of the results could help me decide of the right learning process. The second type of simulations, with var-rational agents, are quick to eliminate. Indeed, in that setting, none of the agents displays the right learning on average, and more importantly in terms of reproduction of results, there is a very high variability of final behaviour, depending on the simulation led. Actually, agents 1 in that type of simulation sometimes increase speculation and sometimes decrease it over time, and this is why the MSD is so high compared to the average value.
However, in both of the other settings, agents of type 3 do speculate much more than they should do if I had succeeded in reproducing Duffy’s model. Duffy’s agents of type 3 never speculate, and mine always get to a level of speculation that is equivalent to the one of agents of type 1 or even higher. None of the results can here be considered as good, since simulations of type 1 see on average a decrease in learning to speculate, and simulations of type 3 have agents 2 learn less efficiently than the others.
However, as can be seen in table 7, this result is really due to the interaction among all learning agents: as soon as one makes some of these agents be automated, agents of type 1 do learn how to behave in the most efficient way. One can note that Duffy’s simulation results are much closer than mine to the data he obtained by doing his experiments, be it for raw values of for representing trends of learning in homogenous simulations.
Table 7: Duffy’s results and my results for simulations of all types with agents 2 and 3 being automated and agents 1 being either: rational agents, var-rational agents and stable agents. I ran 100 simulations, among which some results were not suitable because the time of simulation was too short and agents did not have the opportunity to speculate. Then I took the average and MSD over the remaining simulations (over 90) of the speculation rate for each half of simulation for each t type of agents.
|
|
|
Agents
type 1
|
Agents
type 2
|
Agents
type 3
|
|||
|
|
|
Time-step for the first half |
Time-step for the second half |
Time-step for the first half |
Time-step for the second half |
Time-step for the first half |
Time-step for the second half |
|
Duffy: Average on 5 sessions |
Average
speculation rate |
0.62 |
0.73 |
1.00 |
1.00 |
0.00 |
0.00 |
|
|
|
|
|
|
|
|
|
|
SIM 1’ Rational agents |
Average
speculation rate |
0.91 |
1.00 |
1.00 |
1.00 |
0.00 |
0.00 |
|
MSD |
0.04 |
0.01 |
0.00 |
0.00 |
0.00 |
0.00 |
|
|
|
|
|
|
|
|
|
|
|
SIM 2 ‘ var-rational agents |
Average
speculation rate |
0.80 |
1.00 |
1.00 |
1.00 |
0.00 |
0.00 |
|
MSD |
0.15 |
0.05 |
0.00 |
0.00 |
0.00 |
0.00 |
|
|
|
|
|
|
|
|
|
|
|
SIM 3 ‘ Stable agents |
Average speculation
rate |
0.80 |
0.88 |
1.00 |
1.00 |
0.00 |
0.00 |
|
MSD |
0.00 |
0.05 |
0.00 |
0.00 |
0.00 |
0.00 |
|
In his paper, Duffy suggests that another indicator is pertinent to compare his results with experimental data, which is the individual behaviour of agents along the time. He shows that individual behaviours of his agents are pretty similar to the ones of real humans, in the sense that any agents gets to a very stable behaviours, be it to speculate or to refuse speculation at any possible time. In my simulation, this type of behaviour tend to take place too, although I haven’t been able to test it in a systematic way, neither could I have able to compare to data obtained with real humans, anyway, except by asking John Duffy for his whole set of experimental data.
5. Discussion
5.1. Experiments
The comparison between experimental results and the building of artificial society is an exercise that is now spreading in economics, certainly due to the fact that in both fields, researchers are keen to identify, model and test the actual behaviour of individuals when faced with some economic choices. Experimental economics research is based several steps (Smith, 1994). First, the production of a setting where individuals will face an institution that is alike some theoretical settings, sometimes it can be the production of a controlled market, sometimes the production of a game-like situation (“game” understood as in “game theory”): it is always a very archetypical setting in which the role, ability to act, and communication rules for each actor are very clear, quite limited and very easy to observe. Then comes the organisation of experiments in which researchers isolate humans to make them play the defined game, observe their behaviours according to the limited number of actions that can be performed. Eventually, there is the interpretation, in which the actual behaviours are compared to the one that would be predicted by economic theory, and some conclusion drawn about differences of rationality between real actors and the economical-perfectly informed agent.
Vernon Smith (Smith, 2002) explains that no experiment can actually destroy a theory, but that it can be used to ask new questions, and more importantly to identify situations where theory cannot help anticipate all results, hence the limits of existence of a phenomena. This approach is very close to what most researchers using artificial agent-based worlds do state: simulations are not used to create an alternative theory but to try to express situation that do or do not fit, and hence enrich the expressiveness of description of the science at stake. Issues are just not the same as the one of theory, since both research area are more concerned by applicability than by building a positive result.
Here Duffy used his experiments as a benchmark to test his ability to elaborate a model of learning algorithm. He then used the results of his simulations to build two new experimental settings in which he expected to have forced the agents into more speculative behaviour. I want to discuss this possible use of simulation data into the discussion after explaining the different reasons why it is possible that my results are so different from Duffy’s ones.
5.2. Comments on the difference between my simulations and Duffy’s
When it comes to the very important differences that were witnessed between the simulations, one can first assume two problems that are more of a technical type:
1. the algorithms I use are wrong. This is the first hypothesis: I made mistakes in reproducing the code. My only problem with this assumption is that I followed carefully the paper that has been published, and, when unsure, asked the author himself for his actual choices. Even more, waiting for his (quick) answer, I designed some parallel experiments “in case”. After checking and counter-checking, following simulations step-by-step, I have not eliminated the idea of a mistake of my side, but in that case, I would tend to be worried about transmission of model via papers, and advocate for a more general sharing of code[7].
2. the system is dependent to random generators. In his paper, Duffy specifies well that he tried several random generators to make sure there was no dependence to it and concludes that he is only observing structural results. In my work, I used a random generator that had been built by a student in my team for his master degree in computer science, and that had been proved to be a good uniform law (). This dependence to random generator is really a problem in all cases, since it is used to match agents as well as to define their choice algorithm. However, I have no t enough knowledge nor data from Duffy’s work to be able to check the importance of that element in the differences between results.
To my mind, there are a few more issues that rely more of a theoretical ground:
1. Although I know that Duffy chose to build his model so that to fit the experimental setting, and thus be able to compare simulations to experimental data, I still think that the system is too small and simulations are to short to be able to draw conclusions[8]. It is known by social modellers, although not so often published, that systems where learning is based on meetings are very dependent on first time-steps (Rouchier, 2000). Here we are dealing with a very quick reinforcing process that is study in a small society for a short time. One can hence assume the high dependency of results to first meetings, and thus that the global results can vary in an important way, making it difficult to draw conclusions. What is clear in Duffy’s paper is that individual results are qualitatively similar to the ones in experiments. However, the variability of results, in experiments that were quoted by Duffy, as well as in the simulations, and the differences between global results (since agents, even though they are regular in their behaviour, may choose the worst attitude) is a good sign that the learning process is not necessarily well represented. All one can say is that a quick reinforcement process has been put in artificial agents’ mind, but there is no way to prove it is the one that humans use.
2. One fact is a bit annoying when it comes to these considerations: the number of exchanges in these simulations is very low (no more than 1 out of 4 meetings on average), as well as the consumption rate (maximum I ever got was 1,5 goods consumed on average at each time-step), means that there are really few actions, and hence mainly negative information for agents, which can have an influence on the learning processes[9]. It seems to me difficult to actually judge a cognitive process without going through an analysis of meetings probabilities to explain the evolution of representation. The use of meeting probabilities is indeed the original approach, which Kiyotaki and Wright did analyse, and it turns out to be quite central in the analysis of results here, even if the agents are not themselves aware of that element.
3. The way the observation is conducted seems to me a bit too general. Indeed in no simulation has John Duffy actually studied what an artificial agent and a human would do while facing exactly the same type of information. All comparison are based on the series of behaviours that occur during one game. As we saw, all this choices might be so dependent to meetings that it would be worst proposing a new protocol to actually compare human choices to artificial ones. My option would be to link an artificial agent to a human, and have it share the memory of the real actor. At any time-step, it would thus be possible to compare each choice and see if the actual decision process would match sometimes or never. If reproducing and artificial intelligence is the issue, this would be the best way to test it rigorously[10]. The test could be quite simply led, since one would only need the data of actual meetings and exchanges performed for all humans in an experiment. Since the issue for Duffy was not really to test his model but to use his model to have new ideas of protocol, I assume that his test was enough to sustain his intuition.
5.3. Conclusion
In that paper I describe the work I have done re-implementing a model of speculative market that had been adapted to lead multi-agents simulations. The paper was very clear but I however had some problems in re-implementing the model because some paths were let implicit in the original paper. It could have been a problem, had the author been out of touch, because none of my results would match the values that were expected and two of the algorithms I implemented gave results that were very similar.
First I thought that the differences were due to an error in creating the algorithm or building the program. After studying seriously I concluded that this hypothesis should be forgotten, and that made me ask a few questions concerning the generality of the cognitive processes that were built in, that might not be as stable as expected. It also made me wonder about the completeness of the observation protocol and its ability to actually compare local cognitive processes.
In a recent paper, Vernon Smith (Smith, 2002) explains the relation that experimental economics has to keep with theory. The relation has to be of a constant interrogation of one by the other: experiments are based on theoretical hypotheses and the work of experiment design helps to check or deny the limits of applicability of theories; on the other hand experiments cannot actually prove anything about theories but only show the difficulties of application, ask more precise questions that are in scopes that are related to the given theory. Most researchers in multi-agent simulation will recognize their approach in such a dialogue between two methodology.
This proximity in questioning makes it very clear why Duffy decided to create a link between two exploring methods that unable to question the actual rationality of humans in their economical interactions. At all moments, he clearly shows that his aim is to sustain intuition with both methods, so that to be able to design better experiments. In that sense, there is no question that his paper is indeed very interesting to explore some settings where the Kiyotaki-Wright model is even more accurate. However, along the demonstration, comparisons are led to assess the value of the cognitive model John Duffy uses, and this method, along with the presentation of assumption and results, has been criticised in this paper. The issues arose at several level, when I tried to reproduce the results of the paper: first the algorithms were difficult to understand with no ambiguity; then, the indicators that are used might not be the more accurate to prove the adequacy of learning models. Before concluding on the similarity of behaviour of the real and artificial agents of results, I would suggest to build an actual step by step exploration, with a systematic comparison of the choice that would an artificial agent make, when faced with the same information as a human.
Acknowledgements
I
wish to thank John Duffy for his help while writing the paper,
References
1.Basci, E., 1999, Learning by imitation, Journal of Economic Dynamics and Control 23, 1569-1585.
2.Brown, P.M., 1996, Experimental evidence on money as a medium of exchange, Journal of Eco-nomic Dynamics and Control 20, 583-600.
3.Duffy , J, 2001, Learning to Speculate: Experiments with Articial and Real Agents
4.Duffy, J. and J. Ochs, 1999a, Emergence of money as a medium of exchange: An experimental study, American Economic Review 89, 847-877.
5.Duffy, J. and J. Ochs, 1999b, Fiat money as a medium of exchange: Experimental evidence, working paper, University of Pittsburgh.
6.Kiyotaki, N. and R. Wright, 1989, On money as a medium of exchange, Journal of Political Economy 97, 924-954.
7.Marimon, R., E.R. McGrattan and T.J. Sargent, 1990, Money as a medium of exchange in an economy with arti_cially intelligent agents, Journal of Economic Dynamics and Control 14, 329-373.
8.Roth, A.E. and I. Erev, 1995, Learning in extensive{form games: Experimental data and simple dynamic models in the intermediate term, Games and Economic Behavior 8, 164-212.
9.Rouchier J., 2000, La confiance à travers l’échange. Accès aux pâturages au Nord-Cameroun et échanges non-marchands : des simulations dans des systèmes Multi-Agents.
10.Smith Vernon, 1994, Economics in the Laboratory, Journal of Economic Perspectives, Vol. 8, No. 1, Winter 1994, 113-131.
11.Smith Vernon, 2002, Method in Experiment:
Rethoric and Reality, Experimental economics (5), pp 91-110.
6. Appendix