Replication, Replication and Replication
– Some Hard Lessons from Model Alignment
Bruce Edmonds (bruce@cfpm.org) & David Hales
(dave@davidhales.com)
Centre for Policy Modelling (http://cfpm.org)
Nov. 2002
A published simulation model (Riolo et al. 2001) was replicated in two independent implementations so that the results as well as the conceptual design align. This double replication allowed the original to be analysed and critiqued with confidence. In this case, the replication revealed some weaknesses in the original model, which otherwise might not have come to light. This shows that unreplicated simulation models and their results can not be trusted – as with other kinds of experiment, simulations need to be independently replicated.
1. Introductory Discussion
Typically in social simulation, the ultimate modelling target is a social process. The purpose of the simulation is to somehow help us understand that process. The ability of the simulation to aid us in this way is dependent on there being some relation between the simulation and the social process. Frequently this relation is indirect - the simulation is a model[1] of an abstract process, which is related to the social phenomena in a rich analogical way in the minds and writing of the researchers. This conceptual model mediates between the simulation and the phenomena, the purpose of the simulation is to inform the conceptual model, but it is only the conceptual model which directly represents the phenomena[2].
Sometimes modellers attempt to go beyond this indirect relationship between simulation and phenomena to establish a more direct mapping. In these cases the results of the simulation are compared to data models of the phenomena. There are two ways of doing this as a post hoc check on its validity or to calibrate the model – i.e. the simulation is often adjusted until it is, to some degree, in agreement with the data. In either case, the data gained from the phenomena is used to constrain the simulation. In social simulation the data is never sufficient to constrain the model down to uniqueness, rather some aspects of the model are usually partially constrained using data, leaving other aspects to be determined in other ways. These “other ways” can include: expert/stakeholder opinion, prior theory, pragmatic considerations (what is sometimes called “simplicity”), and conceptual models. Many simulations are partially constrained by data in this way and partially determined conceptually.
Unlike attempts to relate a model to social phenomena, (up to this point) simulation models have been usually related to other models purely via intermediate conceptual models, which are usually expressed in natural language. This paper explores the extent to which simulation models can be related to other simulation models so that their results, as well as their intended design, are consistent with each other. That is, the extent to which simulation models can be faithfully replicated in different implementations so they give the same results.
In this paper the authors describe their experience of such replication. This involved replicating a simple published model in two different implementations. This experience has indicated some techniques that seem to be helpful in this process.
The overall conclusion of this paper is that aligning models is very difficult, but very revealing. The process revealed a host of minor bugs and ill-defined implementation issues in simulations that otherwise appeared to be working well and according to their specification. Clearly, simply implementing simulations with respect to a conceptual model and then “eyeballing” their outputs for consistency with the conceptual model and data series is insufficient to ensure the correctness of an implementation. This indicates that, almost certainly, the vast majority of published social simulations do not comply with their authors’ intentions. In some of these cases the differences between intentions and simulations may be minor, in the sense that they do not change the “overall” character of the simulation results (the so-called “statistical signature”). In the others, these differences may be important, so that when run with new parameters one would get results inconsistent with the stated conceptual model or analysis.
This problem is well known in computer science – it is the problem of verification. Formal and/or structured implementation techniques have been developed to aid programmers implement a specification correctly and to check whether the implementation is correct. These techniques may also be usefully applied in social simulation – (VUA/DESIRE hierarchical verification example) uses a hierarchical verification on a very simple MAS. However the complexity of most social simulations means that these techniques will be of limited use in this regard, because the phenomena that social simulations focus on are usually precisely those where new properties emerge (Edmonds 1998).
Traditional computer science methods often assume that we know a prior what the output of a program should be – that is, there are some set of functional requirements that the program should satisfy. Due to the exploratory nature of simulation work, and the focus on “emergent properties”, functional requirements often do not exist. The researcher “discovers” what happens when the simulation is run. Given this, it is often the case that the programmer of the simulation model literally does not know what to expect and therefore cannot easily check (from the output of a simulation run) whether the program is conforming to the specification (even if a very precise specification existed – which it often does not!). See David et al. (2002) for a discussion of this issue.
However, this does not mean that it is impossible to check the correctness of implemented social simulations, since simulations can be independently replicated from the conceptual model and their results checked against each other. By independently implementing and executing a simulation from a single model specification and subsequent alignment of those simulations “hidden parameters” can be uncovered and aligned. If the specification does not include important parameters or mechanisms (since their importance may have escaped the original designer) then this is likely to be revealed by inconsistencies in outputs between the two implementations.
On the whole a published specification and results will focus on specific phenomena (or story). This means the number of results given will be small and rarely cover much of the parameter space. The danger in a single re-implementation is therefore to assume that the models are aligned when the (small set of) given published results are sufficiently close to those produced by the re-implementation. However, to have a high degree of confidence in the similarity of the two implementations would require matching results with runs based on different parameters (of the model) from those used during any previous alignment process. This is similar to the requirement for testing and comparing results in Machine Learning (Mitchell 1997) - that one should not assess the goodness of some induction algorithm based on previously “seen” data (even if the data was only “seen” by the programmer of the algorithm[3]).
If two independent re-implementations are carried out then this problem is alleviated since when both implementations produce results sufficiently close to those given in the published account then the two re-implementations can be compared to each other over a large part of the parameter space (by executing runs based on extreme or arbitrary parameters). If the models are implementing the same underlying process then they should produce results that are sufficiently close with new previously unexplored parameter values. If new parameter values result in non-alignment of the results then either 1) the specification is inadequate and needs to be refined or 2) at least one of the implementations is an erroneous implementation of the specification[4]. Both programmers stating a refined specification (based on their implementation) and cross checking can attack the first problem. Traditional debugging techniques can be applied to the second problem. It would seem logical to start with the former and move to the latter.
2. The model
We re-implemented a model first described by Riolo et al (2001). This model explores how “tags” (observable social cues or markings) can produce co-operation between seemingly[5] self-interested agents. It follows previous models and suggestions (e.g. Holland 1993, Hales 2000)[6].
The model consists of a population of 100 evolving agents. Each agent has two (real valued) traits: a tag τ (where 0 £ τ £ 1) and a tolerance threshold T (where 0 £ T £ 1). Initially the tags and thresholds are allocated uniformly randomly. To start with each agent is given a randomly selected tag value and tolerance value from these ranges.
The simulation is executed for a number of “generations”. In each generation each agent is paired with another agent P times. For each pairing a new agent is randomly select from the population. The randomly selected agent is denoted the “recipient”, the other agent the “donor”. When a pairing occurs the donor decides whether to make a donation to the recipient. A donation is made if the recipients tag is sufficiently similar to the donors tag.
A recipient tag is considered to be sufficiently similar if it is within the tolerance of the donating agent. Specifically, given a potential donor agent D and a potential recipient R a donation will only be made when |τD–τR| £ TD. This means that an agent with a high T value may donate to agents over a large range of tag values. A low value for T restricts donation to agents with very similar tag values to the donor. In all cases donation can only occur when the skill type of the receiving agent matches the skill type associated with the resource. If a donation is made the donating agent incurs a cost, c, and the recipient gains a benefit, b. In all experiments given here, the benefit b = 1 but the cost c is varied as is the number of pairings.
After all agents have been paired P times and made any possible donations the entire population is reproduced. Reproduction is accomplished in the following manner – each agent is selected from the population in turn, its score is compared to another randomly chosen agent, and the one with the highest score is reproduced into the next generation (a form of “tournament selection”). The scores are not carried over into the next generation but calculated afresh each time. Mutation is applied to each trait of each offspring. With probability = 0.1 the offspring receives a new tag (uniformly randomly selected). With the same probability, Gaussian noise is added to the tolerance value (mean 0, standard deviation 0.01). When T < 0 or T > 1, it is reset to 0 and 1 respectively.
3. The Results
Table 1 and Table 2 below show the results given in Riolo et al (2001). Each of these tables shows the average values of the donation rate and tolerance over all the individuals over 30,000 generations and 30 independent runs.
|
Effect of pairings on donation rate |
||
|
Parings |
Donation rate (%) |
Average tolerance |
|
1 |
2.1 |
0.009 |
|
2 |
4.3 |
0.007 |
|
3 |
73.6 |
0.019 |
|
4 |
76.8 |
0.021 |
|
6 |
78.7 |
0.024 |
|
8 |
79.2 |
0.025 |
|
10 |
79.2 |
0.024 |
Table 1. Pairings is the number of times per generation each agent has an opportunity to donate to a randomly encountered other. The donation rate is the percentage of such encounters in which the choosing agent cooperates, that is, donates b = 1.0 at a cost of c = 0.1 to itself. The average tolerance is the average over all agents and all generations.
|
Effect of cost of donating on donation rate |
||
|
Cost |
Donation rate (%) |
Average tolerance |
|
0.05 |
73.7 |
0.019 |
|
0.1 |
73.6 |
0.019 |
|
0.2 |
73.6 |
0.018 |
|
0.3 |
73.5 |
0.018 |
|
0.4 |
60.1 |
0.011 |
|
0.5 |
24.7 |
0.007 |
|
0.6 |
2.2 |
0.005 |
Table 2. The number of pairings is held at P = 3. The recipient benefit his held at b = 1 and the cost to the donor is varied as shown.
These results showed that in this simulation with 100 agents, if one had at least 3 pairings per individual each generation, then you would get a high rate of donation (>60% of all pairings). Similarly this effect holds for cost of donation being as high as 0.4. This indicated that in this model that fairly robust “altruistic” donation was sustainable in this simulation model.
The interpretation that the Riolo et al. paper gave was that the tolerance played a role similar to the defector/co-operator in the Prisoner’s Dilemma problem. A very low tolerance indicated an individual who would not donate to many others (i.e. a defector) whilst an individual with a high tolerance would donate to others (i.e. a co-operator). They summarised their results as follows:
“Strategies of donating to others who have sufficiently similar heritable tags … can establish cooperation without reciprocity”. (Riolo et al. 2001, page 443)
4. Results From First Re-Implementation (Implementation A)
Below are the results from the first re-implementation of the Riolo model (in Java by David Hales). They are also over 30,000 time periods and 30 runs.
|
Effect of pairings on donation rate |
||
|
Parings |
Donation rate (%) |
Average tolerance |
|
1 |
5.1 (3.0) |
0.010 (0.1) |
|
2 |
42.6 (38.3) |
0.012 (0.5) |
|
3 |
73.7 (0.1) |
0.018 (0.1) |
|
4 |
76.8 (0.0) |
0.021 (0.0) |
|
6 |
78.6 (0.1) |
0.023 (0.1) |
|
8 |
79.2 (0.0) |
0.025 (0.0) |
|
10 |
79.4 (0.2) |
0.026 (0.2) |
Table 3. Pairings is the number of times per generation each agent has an opportunity to donate to a randomly encountered other. The donation rate is the percentage of such encounters in which the choosing agent cooperates, that is, donates b = 1.0 at a cost of c = 0.1 to itself. The average tolerance is the average over all agents and all generations. The values in brackets show the difference between these results and the original results given in table 1.
|
Effect of cost of donating on donation rate |
||
|
Cost |
Donation rate (%) |
Average tolerance |
|
0.05 |
73.7 (0.0) |
0.018 (0.001) |
|
0.1 |
73.7 (0.1) |
0.018 (0.001) |
|
0.2 |
73.7 (0.1) |
0.019 (0.001) |
|
0.3 |
73.7 (0.2) |
0.018 (0.000) |
|
0.4 |
61.0 (0.9) |
0.011 (0.000) |
|
0.5 |
45.9 (21.2) |
0.008 (0.001) |
|
0.6 |
8.1 (5.9) |
0.006 (0.001) |
Table 4. The number of pairings is held at P = 3. The recipient benefit his held at b = 1 and the cost to the donor is varied as shown. The values in brackets show the difference between these results and the original results given in table 2.
The results broadly agreed with those of the Riolo model, but the thresholds at which the high donation effect disappeared had shifted. In these results one was getting significant donation rates for only 2 pairings and for costs up to 0.5. However it was at these thresholds that the re-implemented runs showed the greatest variance. With only a limited description and data in the original paper it is difficult to determine where the error was. For this reason the other author re-implemented the model in a different language (SDML[7]), to see if the Riolo et al. results could be implemented.
5. Results from Second Re-implementation (Implementation B)
The results were only generated for 1 run up to 5000 generations and for up to 6 pairings (so confidence over results is lower than for the averages over 30 runs to 30,0000 generation so far) but they strongly indicate that the results match – although here we merely “eyeball” the results and intuit their similarity.
|
Effect of pairings on donation rate |
||
|
Parings |
Donation rate (%) |
Average tolerance |
|
1 |
5.2 (0.1) |
0.011 (0.1) |
|
2 |
42.6 (0.0) |
0.012 (0.0) |
|
3 |
73.3 (0.4) |
0.018 (0.0) |
|
4 |
76.6 (0.2) |
0.022 (0.1) |
|
6 |
78.6 (0.0) |
0.023 (0.0) |
Table 5. Pairings is the number of times per generation each agent has an opportunity to donate to a randomly encountered other. The donation rate is the percentage of such encounters in which the choosing agent cooperates, that is, donates b = 1.0 at a cost of c = 0.1 to itself. The average tolerance is the average over all agents and all generations. The values in brackets show the difference between these results and the initial re-implementation results given in table 3.
In order to further verify that the two re-implementations matched, results were compared over other areas of the parameter space. It was found (after some checking and debugging) that Implementations A and B agreed very closely over a wide variety of parameter settings (we did not find a set of parameter values where they disagreed).
6. What do the results from the three implementations tell us?
Thus we had three models and three sets of results, so that two sets of results aligned but both disagreed with the published conceptual model and results. The situation is illustrated in Figure 1.
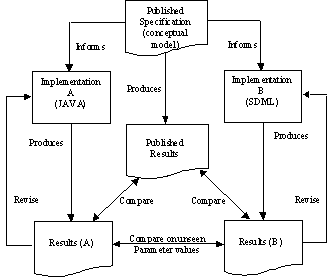
Figure 1. Relationship of published model and two re-implementations
Given that two independent implementations match each other but show significant differences from the original published results we speculated that there were three possible sources of the inconsistency:
· The implementation used to produce the published results did not match the published conceptual model.
· Some aspect of the conceptual model was not clearly stated in the published article
· Both re-implementations had somehow been independently and incorrectly implemented (in the same way).
In some sense these points are not distinct issues but are very much related. It is essentially a matter of opinion as to the sufficiency and clarity of a natural language description of a “conceptual model” for the purposes of re-implementation. However, our argument is that if two independent re-implementations appear to make “the same mistake” then the problem is more likely to lay with the conceptual model description. This would seem to be especially true when the re-implementations align themselves even on previously unseen results from different parts of the parameter space.
7. Three Variants Of Tournament Selection
In order to proceed we reconsidered the original natural language specification of the conceptual model given be Riolo et al. Where we found ambiguity we tried alternative implementations that conformed to the specification.
The problem of interpretation was identified in the tournament selection procedure for reproduction. In the original paper it is described thus:
After all agents have participated in all parings in a generations agents are reproduced on the basis of their score relative to others. The least fit, median fit, and most fit agents have respectively 0, 1 and 2 as the expected number of their offspring. This is accomplished by comparing each agent with another randomly chosen agent, and giving an offspring to the on with the higher score.
It turned-out that in both re-implementations the authors had assumed that when an agent has an identical score to a randomly chosen agent then a random choice is made between them to decide which to reproduce into the next generation (since this is left unspecified in the text). However, when a comparison was made of alternative re-implementations with different reproduction rubrics (when both agents have the same score) it was found that the original implementation must have incorporated a bias towards the systematically selected agent (not the randomly selected agent).
Let us be clearer now (with pseudo-code) as to the three different possible rubrics of reproduction we implemented. Table 6 gives outline algorithms for each of the three rubrics that were implemented.
|
Three Variants Of Tournament Selection |
||
|
LOOP for each agent in population Select current agent (a) from pop Select random agent (b) from pop IF score (a) > score (b) THEN Reproduce (a) in next generation ELSE IF score (a) < score (b) THEN Reproduce (b) in next generation ELSE (a) and (b) are equal Select randomly (a) or (b) to be reproduced into next generation. END IF END LOOP |
LOOP for each agent in population Select current agent (a) from pop Select random agent (b) from pop IF score (a) >= score (b) THEN Reproduce (a) in next generation ELSE score (a) < score (b) Reproduce (b) in next generation END IF END LOOP |
LOOP for each agent in population Select current agent (a) from pop Select random agent (b) from pop IF score (a) <= score (b) THEN Reproduce (b) in next generation ELSE score (a) > score (b) Reproduce (a) in next generation END IF END LOOP |
|
a) No Bias |
b) Selected Bias |
c) Random Bias |
Table 6. Outline pseudo-code algorithms for the three different tournament selection methods tested.
It was found that the authors of both re-implementations had independently assumed that the “no bias” algorithm (Table 6a) was the correct interpretation of the natural language description given in the original published article (see above). However, it was determined that the “selected bias” algorithm (Table 6b) reproduced the results given. Hence it would appear that Riolo et al, used the “selected bias” method and that this was the reason for the different results obtained from the two previous re-implementations. Tables 7 and 8 shows results for each of the algorithms given in Table 6. It is worth noting that the “selected bias” method almost perfectly matches the published results but that this method produces different results from the other two (“no bias” and “random bias”) methods.
|
|
Results From The Three Variants Of Tournament Selection |
|||||
|
|
No Bias (a) |
Selected Bias (b) |
Random Bias (c) |
|||
|
Parings |
Don |
Ave. Tol |
Don |
Ave Tol |
Don |
Ave Tol |
|
1 |
5.1 |
0.010 |
2.1 |
0.009 |
6.0 |
0.010 |
|
2 |
42.6 |
0.012 |
4.4 |
0.007 |
49.6 |
0.013 |
|
3 |
73.7 |
0.018 |
73.7 |
0.019 |
73.7 |
0.018 |
|
4 |
76.8 |
0.021 |
76.9 |
0.021 |
76.8 |
0.021 |
|
6 |
78.6 |
0.023 |
78.6 |
0.023 |
78.7 |
0.023 |
|
8 |
79.2 |
0.025 |
79.2 |
0.025 |
79.2 |
0.025 |
|
10 |
79.4 |
0.026 |
79.4 |
0.026 |
79.4 |
0.026 |
Table 7. Here we compare the results of donation rates (Don) and average tolerances (Ave. Tol) for each of the three different tournament selection algorithms described in table 6 over different “pairings” values. We note that the “selected bias” method very closely matches the published results from the initial model (given in table 1). As before the results are calculated from 30 independent runs to 30,000 generations.
|
|
Results From The Three Variants Of Tournament Selection |
|||||
|
|
No Bias (a) |
Selected Bias (b) |
Random Bias (c) |
|||
|
Cost |
Ave. Don |
Ave. Tol |
Ave Don |
Ave Tol |
Ave Don |
Ave Tol |
|
0.05 |
73.7 |
0.018 |
73.6 |
0.018 |
73.7 |
0.018 |
|
0.1 |
73.7 |
0.018 |
73.7 |
0.019 |
73.7 |
0.018 |
|
0.2 |
73.7 |
0.019 |
73.7 |
0.019 |
73.7 |
0.018 |
|
0.3 |
73.7 |
0.018 |
73.6 |
0.019 |
73.7 |
0.018 |
|
0.4 |
61.0 |
0.011 |
60.5 |
0.011 |
61.0 |
0.011 |
|
0.5 |
45.9 |
0.008 |
26.2 |
0.007 |
46.7 |
0.008 |
|
0.6 |
8.1 |
0.006 |
2.1 |
0.005 |
9.9 |
0.006 |
Table 8. Here we compare the results of donation rates (Don) and average tolerances (Ave. Tol) for each of the three different tournament selection algorithms described in table 6 over different donation cost values. We note that the “selected bias” method very closely matches the published results from the initial model (given in table 2). The results are calculated from 30 independent runs to 30,000 generations.
8. Further investigations into the published model
We had now successfully re-implemented the published conceptual model in two different ways so that they reproduced the published results and were aligned with each other. This gave us confidence that we had implementations that correctly aligned with those that Riolo et al. described in their paper. We could now investigate the full properties of this implemented model, beyond those described.
Although the model was fairly robust with respect to the number of pairings and the cost, we found that the model was far from robust in other ways. In the published model donation occurred if the difference in tag values (of donor and recipient) was less than or equal to the tolerance of the donor (|τD–τR| £ TD). This meant that if the tags of the donor and recipient were exactly the same (what we call ‘tag clones’), then the donor must always donate, since |τD–τR| = 0 and TD³0 by the construction of the simulation. It was found that if the condition for donation was changed to |τD–τR| < TD (i.e. the difference in tag values is strictly less than the tolerance) then the high donation rates achieved in the Riolo model vanished. Table 9 and Table 10 show the corresponding results in this case.
|
Effect of pairings on donation rate (strict tolerance) |
||
|
Parings |
Donation rate (%) |
Average tolerance |
|
1 |
0.0 |
0.000 |
|
2 |
0.0 |
0.000 |
|
3 |
0.0 |
0.000 |
|
4 |
0.0 |
0.000 |
|
6 |
0.0 |
0.000 |
|
8 |
0.0 |
0.000 |
|
10 |
0.0 |
0.000 |
Table 9. Here are the results when all parameters are identical to those used in Table 1 (i.e. the original published results) except that donation only occurs when the differences in tags is strictly less than (rather than less then or equal to) tolerance. As can be seen, donation is completely wiped out.
|
Effect of cost of donating on donation rate (with strict tolerance) |
||
|
Cost |
Donation rate (%) |
Average tolerance |
|
0.05 |
0.0 |
0.000 |
|
0.1 |
0.0 |
0.000 |
|
0.2 |
0.0 |
0.000 |
|
0.3 |
0.0 |
0.000 |
|
0.4 |
0.0 |
0.000 |
|
0.5 |
0.0 |
0.000 |
|
0.6 |
0.0 |
0.000 |
Table 10. Results obtained when all parameters are identical to those used in Table 2 (i.e. the original published results) except that donation only occurs when the differences in tags is strictly less than (rather than less then or equal to) tolerance. As can be seen, donation is completely wiped out.
In this case, where individuals can evolve so that they are not forced to donate to tag clones of themselves the emergent ‘altruism’ does not occur and tolerances quickly go to zero. Further experimentation revealed that the effect reported in (Riolo) was due to the fact that the simulation quickly becomes dominated by a single group of individuals, all of whom have exactly the same tag. Once such a group is established there is a high probability that individuals in this group will be paired with each other and thus donate to each other. The individuals are thus likely to have a higher score that those not in this group, so they are preferentially reproduced into the next generation which reinforces the group.
To test this we also ran versions of the Riolo model where all the tolerances were set permanently to zero. The results of this are shown in Table 11and Table 12 below. These tables show the results for each of the selection methods shown in Table 6.
|
|
Results when tolerance set to zero for different Pairings |
|||||
|
|
No Bias (a) |
Selected Bias (b) |
Random Bias (c) |
|||
|
Parings |
Don |
Ave. Tol |
Don |
Ave Tol |
Don |
Ave Tol |
|
1 |
3.1 |
0.000 |
0.0 |
0.000 |
4.1 |
0.000 |
|
2 |
65.4 |
0.000 |
0.0 |
0.000 |
65.6 |
0.000 |
|
3 |
75.3 |
0.000 |
0.0 |
0.000 |
75.4 |
0.000 |
|
4 |
77.6 |
0.000 |
0.0 |
0.000 |
77.7 |
0.000 |
|
6 |
78.8 |
0.000 |
0.0 |
0.000 |
78.8 |
0.000 |
|
8 |
78.9 |
0.000 |
1.9 |
0.000 |
78.9 |
0.000 |
|
10 |
79.0 |
0.000 |
7.6 |
0.000 |
79.0 |
0.000 |
Table 11. Results when tolerance is forced to be always zero for all agents (i.e. the tolerance mechanisms is turned-off) with all other settings as they were for the original results given in Table 7.
|
|
Results when tolerance set to zero for different Costs |
|||||
|
|
No Bias (a) |
Selected Bias (b) |
Random Bias (c) |
|||
|
Cost |
Ave. Don |
Ave. Tol |
Ave Don |
Ave Tol |
Ave Don |
Ave Tol |
|
0.05 |
75.3 |
0.000 |
0.000 |
0.000 |
75.4 |
0.000 |
|
0.1 |
75.3 |
0.000 |
0.000 |
0.000 |
75.4 |
0.000 |
|
0.2 |
75.3 |
0.000 |
0.000 |
0.000 |
75.4 |
0.000 |
|
0.3 |
75.3 |
0.000 |
0.000 |
0.000 |
75.4 |
0.000 |
|
0.4 |
66.0 |
0.000 |
0.000 |
0.000 |
66.0 |
0.000 |
|
0.5 |
59.7 |
0.000 |
0.000 |
0.000 |
59.8 |
0.000 |
|
0.6 |
17.2 |
0.000 |
0.000 |
0.000 |
20.3 |
0.000 |
Table 12. Results when tolerance is forced to be always zero for all agents (i.e. the tolerance mechanisms is turned-off) with all other settings as they were for the original results given in Table 8.
In these tables we see an interesting (and initially unexpected) result – notice that for the selected bias results we get low donation rates but it is high for both other selection mechanisms. Why is this? Reflection on the nature of the selection mechanisms (see Table 6) offers an explanation for the seemingly anomalous results.
Consider an initial population of 100 agents each with a randomly assigned tag (so almost certainly each agent will have a unique tag value). With tolerance set to zero, and no shared tag values, agents will not donate to other agents – they will never find a partner matching their tag. This means all agents will obtain a score of zero. Using the selected bias mechanism when all agents have the same score will produce the result that the next generation will consist of the same agents as the previous generation with some mutation applied to tags. However tag mutation (either a new tag is assigned with probability 0.1 or the tag is left unchanged) is unlikely to produce agents with matching tags. Consequently there is no scope for groups of “tag clones” to form because there is no chance for agents to produce more than a single copy of themselves into the next generation. This then, implies that all the cooperation we have seen in all runs of the model is a result of agents donating between tag clones (which is built into the assumption of the model – remember agents have to donate to tag clones). This ties in with the previous results showing that donation disappears when the difference between tags must be strictly less than the tolerance (Table 10)[8].
In the other selection cases there is a chance that an agent
may get replicated more than once into the next generation. Now, if we wished
to verify that the tolerance mechanism was significant in producing high
donation and only results from the selected
bias method were examined it would superficially appear that the tolerance
mechanism was driving high donation
because when it was turned off donation appears to disappear. However, as we
see here, the two other selection mechanisms show that this is not the case.
This is important because the original results ascribe the donation process to
the tolerance process, not the particular (and rather peculiar) specific
selection process. The generalisation then, of those original results to
general evolutionary process would appear to be false[9].
In this sense it’s hard to accept the social interpretations of the world as
originally published (Riolo et al. 2001, and Sigmund and Nowak commentary). We note here that, as a direct result of
multiple re-implementations, deeper insight has been gained into important (and
previously hidden) aspects of the model which have major implications with
respect to possible interpretations of the results.
As can be seen in Table 11 and Table 12 the general effect of high donation rates remains in the complete absence of the tolerance mechanism for the no bias and random bias selection methods. As stated above, this is due to both these mechanisms allowing for the chance that an agent may make more than one copy of itself to the next generation (and hence producing a tag clone group).
It could be argued at this stage that the tolerance mechanism might become operative if agents were not allowed to produce clones. So that although the model and results so far are not sufficient to demonstrate a tolerance process promoting cooperation it could work. To test this hypothesis we produced a further simulation in which we introduced a very small but certain mutation of tag values (Gaussian noise with mean zero and standard deviation of 10-6) into the reproduction process so that a group could never exactly clone itself[10]. In this case the tolerance mechanism would have to come into play if a high donation rate was to emerge. But the high donation effect vanished again (see Table 13 and Table 14).
Finally, to see whether the reported effect was robust to changes in population size we ran the simulations with twice the population size (i.e. 200 individuals). Again the donations rates vanished (we have not reproduced these tables since they are identical to Table 9 and Table 10 above).
In this manner we were able to understand how the published model was dependent upon the forced donation among tag clones and that the tolerance mechanism was essentially irrelevant.
It seems that we now understand the published model better than the original authors. A more informative and precise summary of their paper could be:
Compulsory donation to others who have identical heritable tags can establish cooperation without reciprocity in situations where a group of tag clones can replicate themselves exactly
Which is a somewhat less significant result that that claimed in the original paper.
|
|
Results when noised added to tag values on reproduction |
|||||
|
|
No Bias (a) |
Selected Bias (b) |
Random Bias (c) |
|||
|
Parings |
Don |
Ave. Tol |
Don |
Ave Tol |
Don |
Ave Tol |
|
1 |
3.7 |
0.009 |
1.9 |
0.009 |
4.2 |
0.009 |
|
2 |
3.1 |
0.007 |
1.5 |
0.006 |
3.7 |
0.007 |
|
3 |
4.0 |
0.005 |
1.5 |
0.005 |
5.1 |
0.005 |
|
4 |
6.8 |
0.005 |
2.0 |
0.005 |
8.5 |
0.005 |
|
6 |
13.1 |
0.004 |
6.2 |
0.004 |
14.2 |
0.004 |
|
8 |
15.5 |
0.004 |
12.7 |
0.004 |
16.2 |
0.004 |
|
10 |
12.1 |
0.002 |
10.9 |
0.003 |
12.8 |
0.003 |
Table 13. Results when a very small level of Gaussian noise is added to the tag value during the replication process (when an agent is copied into the next generation). Notice that the donation rate drops sharply[11] (over Table 7) – this would not happen if the originally published interpretation held.
|
|
Results when noise added to tag values on reproduction |
|||||
|
|
No Bias (a) |
Selected Bias (b) |
Random Bias (c) |
|||
|
Cost |
Ave. Don |
Ave. Tol |
Ave Don |
Ave Tol |
Ave Don |
Ave Tol |
|
0.05 |
4.0 |
0.006 |
1.5 |
0.005 |
5.1 |
0.005 |
|
0.1 |
4.0 |
0.005 |
1.5 |
0.005 |
5.1 |
0.005 |
|
0.2 |
3.9 |
0.005 |
1.4 |
0.005 |
5.0 |
0.005 |
|
0.3 |
4.0 |
0.005 |
1.4 |
0.005 |
5.2 |
0.006 |
|
0.4 |
3.2 |
0.005 |
1.3 |
0.005 |
3.8 |
0.005 |
|
0.5 |
2.7 |
0.005 |
1.3 |
0.005 |
3.2 |
0.005 |
|
0.6 |
2.5 |
0.005 |
1.2 |
0.005 |
2.9 |
0.005 |
Table 14. Results when a very small level of Gaussian noise is added to the tag value during the replication process (when an agent is copied into the next generation). Notice that the donation rate drops sharply (over Table 8) – this would not happen if the originally published interpretation held.
9. Some practical lessons about aligning models
Here we briefly describe some of the techniques and tips we have learnt that aid the alignment of simulations.
· Check the alignment of simulations in the first time cycles of their runs (possibly averaged over several runs). This indicates whether they are initialised in the same way and the differences may be clearer than after new effects emerge in the simulation or chaos appears.
· Use statistical tests over long-term averages of many runs, using such as the Kolmogorov-Smirnov test (Chakravarti et al. 1967) to see whether two sets of figures come from the same distribution. Often sets of figures that look the same fail this sort of test.
· If two simulations do not align, progressively turn off features of the simulation (e.g. donation, reproduction, mutation etc.) until they do align. Then search for the differences in the reduced model. Then progressively reintroduce the features.
· Use different kinds of languages to re-implement a simulation (we used a declarative and an imperative language) and, if possible, programmed by different people. Failing that, at least use different kinds of program or data structure. Otherwise there is a good chance that any mistakes or assumptions will simply be repeated in both.
10. Discussion
In this paper we have characterised a simulation as a (formal but non-analytic) computational theory[12], which can effectively be checked only via experiment. Each simulation run corresponds to such an experiment.
Give this approach to simulations, much of the established scientific practice on conducting experiments can be applied including:
· That there should be a norm concerning the publication of simulation results, namely that the description of the simulation should be sufficient for others to be able to replicate (i.e. re-implement) the simulation;
· That experiments have to be independently replicated and the results confirmed before the simulation or the results are taken seriously;
· That simulations can not be confirmed as correct but merely survive repeated attempts at refutation, and thus gradually come to be relied upon;
· That it is often more productive if runs of a simulation are directed at particular hypotheses about the simulation process rather than aim to be generally indicative – this has the advantage that data can be collected in a focused way to suit the issue being simulated rather than try to fit the simulation to what data happens to be available.
The difficulties of model alignment are highly suggestive of the difficulties of modelling social phenomena. In model alignment one is attempting to model one simulation with another. To do this alignment one has all the possible advantages: any detail of the target simulation is potentially inspectable; all experiments are repeatable; the design of the target simulation is known and is not extremely complex; the simulations will be partly modular, allowing some features to be tested separately[13]. When modelling observed social phenomena one does not have these advantages – if aligning one computational model against another is hard, how much more so must be truly aligning a computational model with a real world social process!
11. Conclusions
If we had not re-implemented the Riolo model we would not have been able to discover its shortcomings. If we had not re-implemented the model in two independent ways we would not have been able to state with confidence that the shortcomings were inherent in the original model rather than ours. Further, the double re-implementation greatly aided us in finding simulations that aligned with the original. In other words, without double re-implementation, there would have been a distinct possibility that the shortcomings would never have come to light.
Since almost all simulations are not amenable to formal analysis, the only way they can be verified is via the experimentation of running simulations. If we are to be able to trust the simulations we use, we must independently replicate them. An unreplicated simulation is an untrustworthy simulation – do not rely on their results, they are almost certainly wrong!
References
David, N., Sichman, J. and Coelho, C. (2002), Towards an Emergence-Driven Software Process for Agent-Based Simulation. 3rd International Workshop on Multi-Agent Based Simulation (MABS). Bologna, Italy, July 2002.
Blake, C.L. & Merz, C.J. (1998), UCI Repository of machine learning databases [http://www.ics.uci.edu/~mlearn/MLRepository.html]. Irvine, CA: University of California, Department of Information and Computer Science.
Chakravarti, Laha, and Roy, (1967), Handbook of Methods of Applied Statistics, Volume I, John Wiley and Sons, pp. 392-394.
Edmonds, B. (1999), Syntactic Measures of Complexity. Philosophy. Manchester, University of Manchester. http://bruce.edmonds.name/thesis/
Edmonds, B. (1998), Social Embeddedness and Agent Development. UKMAS'98, Manchester, December1998. http://cfpm.org/cpmrep46.html
Edmonds, B. (2000), The Use of Models - making MABS actually work. In Moss, S., Davidsson, P. (Eds.) Multi-Agent-Based Simulation. Lecture Notes in Artificial Intelligence 1979. Berlin: Springer-Verlag.
Engelfriet, J. Jonker, C. and Treur, J. (1999), Compositional Verification of Multi-Agent Systems in Temporal Multi-Epistemic Logic. In Proceedings of the 5th International Workshop on Intelligent Agents V : Agent Theories, Architectures and Languages (ATAL-98), Springer. Lecture Notes in Artificial Intelligence 1555:177-194.
Hales, D. (2000), Cooperation without Space or Memory: Tags, Groups and the Prisoner's Dilemma. In Moss, S., Davidsson, P. (Eds.) Multi-Agent-Based Simulation. Lecture Notes in Artificial Intelligence 1979. Berlin: Springer-Verlag.
Hales, D. (2001), Tag Based Cooperation in Artificial Societies. Ph.D. Thesis, Department of Computer Science, University of Essex (available at: http://www.davidhales.com/thesis).
Hales, D. (2002a), Cooperation and Specialisation without Kin Selection. CPM Working Paper 02-88. The Centre for Policy Modelling, Manchester Metropolitan University, Manchester, UK (http://cfpm.org/cpmrep88.html).
Hales, D. (2002b), Smart Agents Don’t Need Kin – Evolving Specialisation and Cooperation with Tags. CPM Working Paper 02-89. The Centre for Policy Modelling, Manchester Metropolitan University, Manchester, UK (http://cfpm.org/cpmrep89.html).
Hales, D. & Edmonds, B. (2002) Evolving Social Rationality for MAS using “Tags”. CPM Working Paper 02-104. The Centre for Policy Modelling, Manchester Metropolitan University, Manchester, UK (http://cfpm.org/cpmrep104.html).
Holland, J. (1993), The Effect of Labels (Tags) on Social Interactions. SFI Working Paper 93-10-064. Santa Fe Institute, Santa Fe, NM.
Mitchell, M. (1997), Machine Learning, McGraw Hill.
Riolo, R. L., Cohen, M. D. and Axelrod, R (2001), Evolution of cooperation without reciprocity. Nature, 411:441-443.
Sigmund, K. and Nowak, M. A. (2001), Evolution – Tides of tolerance. Nature 414:403.