Majoros, W. (2002). Syntactic Structure in Birdsong: Memetic Evolution of Songs or Grammars.
Journal of Memetics - Evolutionary Models of Information Transmission, 6.
http://cfpm.org/jom-emit/2002/vol6/majoros_w.html

---

Abstract

Introduction

1 - Anecdotal Evidence for Syntactic Structure in House Finch Song

2 - Evolutionary Advantages of Grammar-Based Song Generation

3 - Overview of the Experimental Approach

4 - Methods

4.1 - Sound Recording

4.2 - Selection and Transcription of Recordings

4.3 - Grammar Induction

4.4 - Contingency Table Analysis

4.5 - Simulation of Memetic Evolution of Songs

4.6 - Regression Analysis

5 - Results

5.1 - Properties of House Finch Data

5.2 - Properties of Simulated Data

6 - Discussion

7 - Conclusion

Acknowledgments

References

Abstract

In order to ascertain whether the units of memetic transmission and recombination in the birdsong of a particular species of finch exist at the level of individual songs or instead at the level of grammar models, a large number of songs were subjected to grammar induction techniques and the resulting grammars analyzed for key structural properties considered indicative of the existence of an underlying grammar. The weight of evidence provided by this approach was judged by applying the same analyses to the results of a genetic algorithm applied to a synthetic repertoire of songs and comparing the results. Memetic evolution applied directly to song elements, as simulated by the genetic algorithm, was found to generate models very similar to those inferred from the House Finch song, thereby demonstrating that the problem of discerning between these two competing hypotheses for explaining the syntactic structure observed in House Finch song is not easily solved using the limited data obtainable in the field. This underscores the importance of experimental rigor when studying memetic systems, and leaves open the question of how to confidently determine the actual level at which memes are operating in a particular system.

Introduction

---

1. Anecdotal Evidence for Syntactic Structure in House Finch Song

It is reasonable to inquire, however, whether singing behavior may have a more algorithmic basis than the simple recitation of fixed songs. In particular, linguists have devised a standard hierarchy of so-called "grammars," called the Chomsky hierarchy [8], which classifies increasingly sophisticated methods for the generation of strings of symbols [note 1]. For species exhibiting considerable complexity in the structure of their songs, it is tempting to speculate on the possible existence of grammar-like mechanisms in their behavioral programming [note 2].

The House Finch (Carpodacus mexicanus) is clearly one of those species. Various authors have noted the complex and variable syntactic features of the song of this Fringillid. Mundinger [12] observed that in one region of his study area, "each male sang a wide variety of patterns, and individual variation in a given pattern was high." He also pointed out that "the precise mechanism of song learning in the wild is unknown" [note 3]. Bitterbaum and Baptista [1], working in California, noticed that "not only do no two birds sing exactly alike, but even a single bird seldom repeats himself precisely." Pytte [14] likewise observed in Wisconsin that "rarely is the same song repeated exactly" and concluded that "song types reported in this study appear to be largely an artificial construct."

Various authors have reported having the strong impression that many songs had been formed through the recombination of portions of other songs ([1, 14,16,18]). Tracy and Baker [18] speculate that "birds may be memorizing song components (syllables or phrases) that are strung together into complete songs at a later time" and Pytte [14], in relating the work of Bitterbaum and Baptista [1], explains that "juveniles learn individual syllables as units, which they segregate and recombine independently during song production."

However, these statements apparently refer only to subsong production by juveniles. As Lynch and Baker [10] stated more explicitly regarding recombination of song elements in the Chaffinch (Fringilla coelebs), "As song development proceeds, songs become less variable; by the time they reach 'crystallization,' they are highly stereotyped, and hybrid songs tend to disappear from the birds' repertoire."

Smith [16], on the other hand, offered the following intriguing proposal: "It is possible that house finches do not even choose songs or song elements, but choose a model(s) to imitate. Variation would then come from the 'mutations' of the model." Although he provides no further elaboration on the type of model that he has in mind, the fact that his work involves the construction of Markov chains from House Finch songs is highly suggestive; Markov chains are a simple form of grammar model [note 4]. However, Smith's models were inferred not from the songs of individual birds, but from the songs of all the birds in the local population in a given year, so it is not clear that these models are intended to describe anything other than the overall structure of the local dialect. Furthermore, the models were inferred in a highly subjective way; phrases do not appear to have been selected systematically, and "hybrid" phrases were excluded from the model.

---

2. Evolutionary Advantages of Grammar-Based Song Generation

---

3. Overview of the Experimental Approach

In order to test this hypothesis, I further posited that memetic evolution applied directly to songs represented as fixed syllable sequences would be incapable of generating certain statistical properties expected to occur in actual House Finch song. In particular, I posited that contingency tables constructed from pairs of states in the inferred grammar models would provide support for independence between the choices made at those pairs of states as the birds transitioned out of those respective states during song generation. Intuitively, one would not expect such independence to obtain in grammar models inferred from songs that had instead been generated via simple string recombination, because there is no obvious reason to expect random crossover between songs to respect phrase boundaries in such a way as to maintain the symmetry necessary for independence at pairs of states in the corresponding inferred grammar.

Although such independence may be expected to occur in extreme cases where extensive recombination has produced nearly all possible syllable combinations, such an extensive shuffling of syllables would seem to obliterate certain forms of order observed in actual House Finch song. For example, the models inferred in Smith [16], as well as unpublished analyses of data from Pytte [14] performed by myself reveal persistent multi-syllable themes that one would not expect to survive in the presence of high levels of random crossover.

---

4. Methods

4.1 Sound Recording

Recording equipment consisted of a 31-inch Telinga Pro Universal parabolic reflector fitted with a Sennheiser ME62 microphone, and a Marantz PMD222 portable cassette recorder. Songs were recorded onto Maxell high-bias (CrO₂) cassettes in the field and then digitized using 18-bit A/D conversion hardware and written to compact disk (CD-R).

Male House Finches were located by walking along a road and listening for song. When a singing finch was encountered, recording of that bird began immediately and continued until the bird ceased singing, the end of the current tape was reached, or another singing House Finch intruded upon the session. Thus, a single recording on the tape consisted of song from only one bird. Although the same bird may be represented in multiple recordings taken at a single site, this will not affect the grammar induction process, which was performed only within individual recordings.

4.2 Selection and Transcription of Recordings

Individual songs in the selected recordings were separated based on a subjective assessment of inter-song delay. House Finch songs are generally separated in time by a delay much longer than that between the individual syllables of a song (pers. obs.), so this process is largely unambiguous and replicable. Each song was stored in a separate file in ".wav" format. Recordings consisting of fewer than fifteen songs were omitted from the analysis.

Sonograms were produced using the Spectrogram 2.3 software [9] and printed out on a 1440 dpi photo-quality printer for manual analysis. Individual syllables were subjectively identified by spacing. Although a syllable often consisted of a single "trace" in the sonogram, some syllables consisted of multiple traces which were positioned very close together (in time) and which consistently occurred together in all sonograms. Thus, the process of separating syllables is rather more subjective than that of identifying individual songs, but a relatively high degree of reproducibility should be expected nonetheless.

Syllables were compiled into site-specific "alphabets," with a single alphabet being associated with all of the birds recorded at a single site. Each syllable was assigned a unique symbol, and songs were then translated into sequences of these symbols. These steps were all performed by a single person, in order to eliminate any inter-observer differences.

4.3 Grammar Induction

The first step in inferring a model was to identify common subsequences with which to label the states. This was accomplished by computing a multiple alignment between songs [note 8], using techniques developed for molecular biology. Beginning with the first pair of songs in the session, pairwise alignments were computed using the Needleman-Wunsch global alignment algorithm [3] between each successive song and the overall consensus sequence of the foregoing alignments, with individual syllables being treated as residues for the purpose of alignment. The alignment algorithm was parameterized as follows: gap open penalty = 1.5, gap extension penalty = 0.66, match score = 100, and mismatch penalty = 1000. This parameterization effectively precluded the alignment of nonidentical syllables [note 9].

Gaps in the alignment were used to infer breaks in the consensus sequence, with a break being established immediately left of the beginning of each gap and immediately right of the end of a gap. The consensus sequence was then segmented into the substrings delimited by these breaks, with an implicit break occurring at the beginning and end of the sequence. Each such substring was then assigned as the label of a state, with identically labeled states being merged into a single state.

Because of the manner in which breaks were inferred, songs could be unambiguously recoded as sequences of states, based on the positions of their constituent symbols in the multiple alignment relative to the breaks. These state sequences were then used to establish the state transitions by observing which states immediately followed which others in the recoded songs, much the way one goes about training a Markov chain [3]. Start states and final states were identified by their occurrence at the beginnings and ends of songs, respectively.

Grammar models were visualized using the daVinci program [19].

4.4 Contingency Table Analysis

In order to test for independence between the choice of transition made at pairs of states within individual songs, a contingency table was constructed for each such pair of states. In particular, for each pair of states <X,Y> such that Y follows X (potentially after some number of intervening states) in at least one song and such that both X and Y offer transitions to at least two successor states (fig. 1a), a 2x2 contingency table was constructed by tabulating the occurrences of the four combinations of transitions leaving X and Y (<left,left>, <left,right>, <right,left>, <right,right>) in all of the songs from the current recording session (i.e., for a single bird). In cases where more than two transitions left a state, all pairs of outgoing transitions from that state were considered separately, so that only 2x2 contingency tables were constructed. 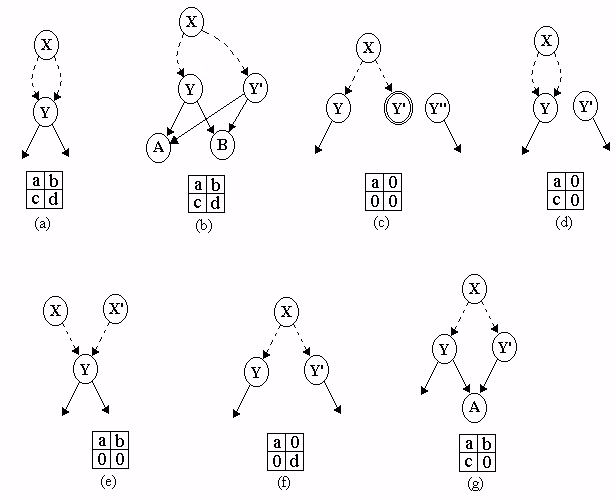As an additional constraint on which of these state pairs would be considered, it was required that state Y be reachable from state X by at least two different paths.

Figure 1: (a) Contingency tables are naively assumed to arise from the depicted topology. Solid lines are transitions and broken lines indicate arbitrarily long paths. (b) A four-entry table could result from the merging of identically labeled states Y and Y', but only if both have transitions to A and B. (c) A single-entry table could result from the merging of states Y, Y', and Y'', where Y' is a final state. (d) One form of two-entry table can be formed by merging Y and Y'. (e) Another form of two-entry table can be formed by merging X and X'. (f) Yet another form of two-entry table can be formed by merging Y and Y' in the topology shown. (g) A three-entry table can be formed by merging Y and Y', but only if both have transitions to A.

Probabilities were assigned to contingency tables using the Fisher Exact Test [21] under the assumption of independence. Because a potentially large number N of such tests were to be conducted, an adjusted critical value was computed as follows:

or, equivalently,

Using this computed a as the critical value sets the probability of committing at least one Type I error during the N tests to 5%.

Any particular statistically significant table is evidence only of a single instance of erroneous
state-merging during model induction. A large number of significant tables would suggest that no state merging is appropriate, thereby seriously calling into question the applicability of this class of models. As previously mentioned, a small number of significant tables suggests only that the grammar induction algorithm commits occasional state-merging errors.

However, tables with four nonzero entries would seem to constitute positive evidence for the validity of this class of model, because a spurious four-entry table (regardless of P-value) would require not only erroneous state merging, but also the coincidental matching of transitions leaving such erroneously merged states (fig. 1b). Such a high level of coincidence is not required for the spurious generation of tables having one or more zero entries (fig. 1c-1g), with the possible exception of single-entry tables (fig. 1c). However, single-entry tables were deemed less informative than four-entry tables for the current application, because statistically nonsignificant single-entry tables tend to have very small entry sums, and they are therefore indicators primarily of inadequate sample size. Obviously, statistically significant tables with any number of nonzero entries were considered informative.

A large number of four-entry tables would therefore seem to be highly unlikely without the existence of an underlying grammar model of the type proposed, unless those tables were judged statistically significant by the Fisher Exact Test.

Unfortunately, the complexities of these grammar models make reliable estimation of probabilities for various types of grammar induction errors exceedingly difficult without adequate sample sizes. Because the number of possible paths through a model grows exponentially with the number of transitions, sample sizes obtained in practice can be expected to be woefully inadequate; therefore, a rigorous analytical treatment was not deemed practical.

My approach to compensating for this lack of rigor was to apply the same contingency table analysis to sets of simulated songs generated without the use of a grammar model (see below); any support for the existence of a grammar model obtained from this simulated data would nullify the value of any corresponding evidence found in the House Finch data.

4.5 Simulation of Memetic Evolution of Songs

Briefly, an initial population of 14 to 25 strings of 13 to 24 unique symbols drawn from nonoverlapping alphabets was subjected to between 14 and 40 generations of panmictic and selectionless evolution. During each generation, 15 new strings were generated by applying two-point crossover to pairs of strings selected uniformly at random from the current population. Each new string then replaced an existing string at random. A two-point crossover operation combines the beginning and ending portion of one parent string with the middle portion of another parent string, to produce a new child string. The crossover points are selected at random. Note that differently-sized parents were allowed to recombine, and crossover points were allowed to vary between the two parents, thereby facilitating the creation of repetitive elements and further variation in string length.

The final population at the end of each run was then subjected to the grammatical inference algorithm described above to infer a grammar model which was in turn subjected to contingency table analysis. Several thousand runs were performed under varying parameterizations until several grammar models were obtained which adequately matched those inferred from House Finch song according to various criteria.

In particular, the following quantities were required to differ by no more than one (sample) standard deviation from the expected values established by the House Finch data: number of states, number of transitions, transition density, mean state label length, mean in-degree, mean out-degree, number of start states, number of final states, number of cycles, mean cycle length, number of unique syllables, and mean song length. In-degree and out-degree are the numbers of transitions entering and leaving a state, respectively. Transition density is the proportion of combinatorically possible transitions realized. Cycles were identified by observing back-edges during a depth-first-search originating at each start state [2]; no attempt was made to identify composite cycles, so cycle sizes and counts are somewhat underestimated.

To summarize the intent of these experiments, my prediction was that four-entry contingency tables would be common in the House Finch data, with no more than a few of these being statistically significant, thereby demonstrating independence between transition choices made at different states during the generation of a song, and thus supporting the possibility that House Finches actually use some form of grammar model to generate their songs anew at each performance. In contrast, I predicted that the simulated data would produce either very few four-entry tables, or that most of these would be statistically significant, thereby supporting the intuition that syntactic structure of the type observed in House Finch songs would be highly unlikely to occur by chance if House Finches were simply reciting fixed songs that changed only through transmission "errors" during cultural evolution.

4.6 Regression Analysis

Except where noted, all analyses were performed using unpublished software written by the author.

Means are given ± SD.

---

5. Results

5.1 Properties of House Finch Data

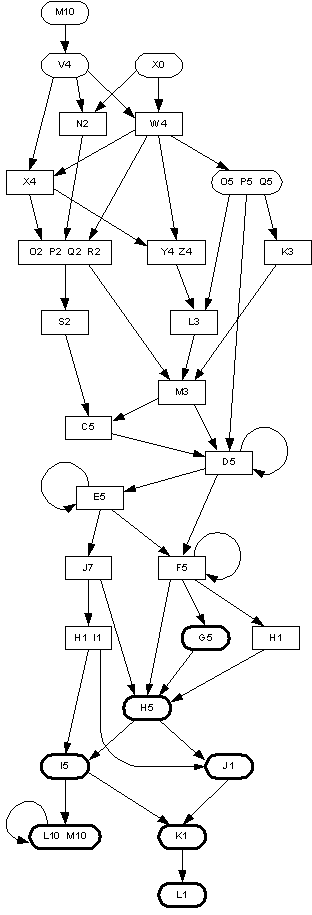
An example model inferred from the field data is shown in figure 2. There was considerable diversity in the overall structure of the topologies observed. In particular, not all of the models were long and narrow like that shown in figure 2, some had states with longer labels, and some had larger cycles than shown in the example.

Figure 2: An example of a grammar model inferred from songs produced by a House Finch. Rectangles denote states, thin-lined ellipses denote start states, and thick-lined ellipses denote final states. Transitions between states are shown as directed arrows.

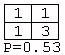
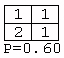
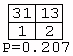
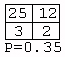
Of the 3,282 tables, only one (0.03%) had a P-value less than 0.05. This was:

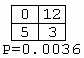
However, due to the large number of tests conducted, an event with this probability could be expected to occur several times; the adjusted critical value given N=3,282 is 0.000016. Even if tables that extreme could not possibly be obtained with the given sample size, the fact that far fewer than 5% of the tables had a P-value of less than 0.05 supports the decision not to reject the assumption of independence.

The number of transitions in the inferred grammar models was found to vary linearly with the number of states (m=1.22, b=-1.81, r²=0.97; t=38.816, P<0.001), as shown in figure 3. Because the number of transitions combinatorically possible between n states varies with n², this linear relationship places appreciable constraints on the topological structure of the models.

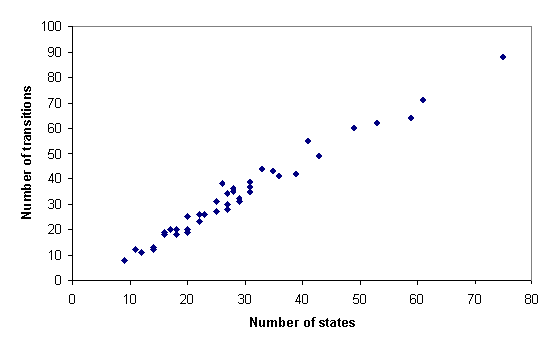
Figure 3: Number of transitions (vertical axis) as a function of the number of states (horizontal axis) in grammar models inferred from House Finch songs.

5.2 Properties of Simulated Data

Figure 4: An example of a grammar model inferred from simulated songs produced by a genetic algorithm.

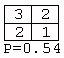
This particular run produced a single four-entry contingency table:

A total of approximately 300,000 contingency tables were obtained during approximately 5,200 runs. Of these tables, 3,128 (1.04%) had four nonzero entries, and only 47 (0.02%) were significant at the 0.05 level. Thus, the simulations produced proportionally more four-entry tables and proportionally fewer statistically significant tables than analyses of the House Finch data.

As with the field data, the models inferred from simulated data exhibited a wider variety of topologies than can be communicated by a single example such as that given in figure 4. Like the House Finch songs, the simulated data gave rise to topologies with varying numbers and sizes of cycles, varying numbers of states and transitions, and clearly discernible variation in overall structure.

Table 3 gives the mean values of the previously-identified key quantities from a sample of 1000 runs. With the exception of the number of final states, all of the values are within one standard deviation of the mean values observed in the field data. Although this numeric agreement resulted from a conscious effort to match these quantities to the field data via refinement of the parameters to the genetic algorithm, the fact that such agreement could be achieved between these two systems is notable.

As with the field data, the number of transitions was found to vary linearly with the number of states (m=1.57, b=4.19, r²=0.75; t=17.240, P<0.001), as shown in figure 5.

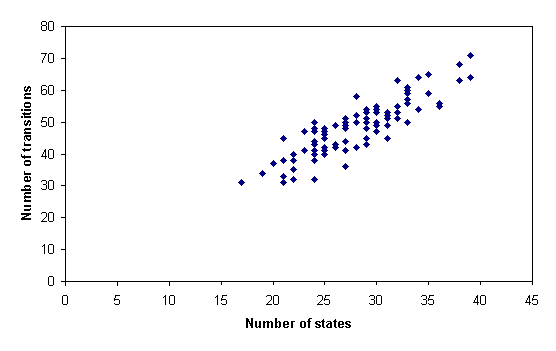
Figure 5: Number of transitions (vertical axis) as a function of the number of states (horizontal axis) in grammar models inferred from simulated data.

---

6. Discussion

Lacking clear and compelling evidence for the existence of grammar rules in House Finch singing behavior, one might be tempted to invoke the principle of parsimony to establish rote memorization as the preferred hypothesis. However, it is not clear that either of the two hypotheses considered here (rote memorization vs. grammatically constrained improvisation) is significantly more parsimonious than the other. Although rote memorization would appear to be a simpler task than grammar induction, the potential for data compression afforded by a grammar model can lead to significantly greater space efficiency. Thus, while grammar models may be more complex in acquisition and operation, they are generally less complex in memory requirements and might therefore demand preference under a Minimum Description Length philosophy [15].

Thus, the question of whether House Finches generate their song using some form of grammar model remains unanswered, and it is questionable whether data collected in the field can definitively resolve the issue. What is likely needed is a set of controlled laboratory experiments, where large samples can be obtained from each bird and where training material can be specifically designed to create various informative testing scenarios.

An important point which has heretofore not been emphasized is that the hypothesis being considered is not simply that House Finches utilize some grammar model in generating their song, but that they specifically adopt a model which accounts for patterns that they identify in training songs. Thus, it is conceivable that controlled experiments might be designed which were capable of detecting a bird's ability to identify and recreate syntactic structures in the songs of an artificial tutor. The task is essentially one of distinguishing between concept learning versus rote memorization in a complex adaptive system.

Failure to foresee the results of the memetic simulation is perhaps attributable to the interaction between the shuffling effects of random crossover and the propensity of sampling error to create spurious order. The same susceptibility can be expected whenever a grammar induction algorithm is applied to moderately sized samples. Even for a collection of strings known to have been generated using a grammar model, one should not expect a black-box algorithm to reconstruct that model with complete accuracy in even the majority of cases. Not only are sample sizes generally limited in practice by the difficulties of working in the field, but grammar induction algorithms are truly only heuristics, and are guaranteed to correctly reconstruct the original grammar only under special circumstances ([4, 5, 13]), which may not obtain in practice.

If it can be demonstrated that House Finches do indeed employ syntax rules in the generation of their song, then a next step would be to characterize the range of complexity possible in those rules. This would require analysis of bird song from a diverse range of geographical locations, because the structural properties of song recorded in one locale can be highly sensitive to the evolutionary history of the local song tradition. That significantly different conclusions could be drawn from different populations of House Finches can be clearly seen by comparing the results of research conducted in different regions of the U.S. (Mundinger [12] in New York and Connecticut, Bitterbaum and Baptista [1] in California, Pytte [14] in Wisconsin, and Tracy and Baker [18] in Colorado).

Alternatively, if direct song recombination is ultimately established as the mechanism behind the evolution of and apparent order observed in House Finch song, then it is conceivable that syntax analyses may still be useful in elucidating some of the parameters of that evolutionary process. Furthermore, the recombination mechanism need not be as simple as the two-point crossover approach used here. The details of this recombination remain to be determined. All of this would require large-scale analyses.

There does not appear to be any logical way to distinguish between the use of grammar models by juveniles which later crystallize their song into fixed syllable strings versus the direct use of syntax rules by singing adults without resorting to invasive techniques such as neuronal monitoring of singing birds, and it is doubtful that current technology and neuroanatomical knowledge are adequate for such an undertaking [11].

Finally, Lynch and Baker [10] predicted that a "general theory of cultural evolution in bird song" would eventually emerge. Before this can happen, the actual nature of memes in bird song must be determined. Lynch and Baker [10] defined memes as syllables and sequences of syllables, but they did not consider higher-level structural elements, such as state transitions or syntax rules. Only a greater understanding of bird song generation will determine whether such extensions to their quantitative theory of cultural evolution are necessary. As stated recently by Greene [7], "We currently lack a coherent conceptual model that explains the diversity of singing behavior and song learning programs in an evolutionary framework."

---

7. Conclusion

Although song-centric models are perhaps the most natural and convenient way for human researchers to conceptualize vocal behavior in birds, until we have a more thorough understanding of song learning and performance in species having complex song, more sophisticated models of song structure such as those considered here should be viewed as valid avenues of investigation. Given the potential complexity of these models, addressing such important issues as the selective advantage they confer, their impact on the form and rate of cultural evolution, and the bias they exert on observed syntactic structure in bird song should make for challenging and fascinating topics of future research.

---

Acknowledgments

The views expressed in this paper are mine alone, and not necessarily those of my employer.

Notes

1. Grammar models generally consist of an alphabet of symbols and a mathematical construct specifying the way in which those symbols can be combined to generate strings, or finite symbol sequences. For birdsong, we can take the individual syllables comprising a song to be the symbols and the entire song to be the generated string. Two prominent classes of grammars in the Chomsky hierarchy are the regular grammars and the context-free grammars. Context-free grammars are the more powerful of the two, and involve the use of productions, or rewrite rules (such as "X can be replaced by ABC") that may be recursively applied to transform an initial string of variables into the final observed form of the string. Context-free grammars are in general implicated in processes that generate matching pairs of symbols, and palindrome-like patterns. Regular grammars, which constitute a proper (and less powerful) subset of the context-free grammars, are equivalent in their computing power both to regular expressions and finite automata (also called finite state machines), which consist of states and transitions, and which are often depicted as small circles with arrows connecting them into allowable paths.

 
2. This is in no way meant to imply, however, that all, or even most, bird species utilize grammars for song generation. Many species have song which is too simple or too stereotyped to suggest utilization of a grammatically-constrained, stochastic song generation procedure. On the other hand, it is not unreasonable to consider grammar-like mechanisms that may be at play as songs change over evolutionary time, or to consider the use of grammatical theories to describe the syntactic structure of songs produced by birds which are not themselves using grammars to generate their song. However, this work is concerned only with the possible use by birds (House Finches in particular) of grammar models during singing behavior.

 
3. Mundinger [12] refers to an unpublished manuscript that deals with song learning in this species, but the manuscript in question actually describes experiments involving the training of House Finches in the laboratory by another species of bird [pers. communication], and I know of no other work to date that examines song learning in this species, either in a controlled setting or in the wild.

 
4. Markov chains and hidden Markov models (HMM's) are generalized forms of stochastic finite automata which provide explicit transition probabilities and (in the case of HMM's) emission probabilities. The model begins in the start state and moves at random from state to state, according to the transition probabilities, emitting a symbol or string of symbols upon entering each state, until a final state is reached. In this way, the model generates a string consisting of the concatenated symbols emitted by the states that were visited during operation of the model. In HMM's, the emission probabilities of a state determine what symbol is emitted when that state is entered, whereas in a Markov chain, there is only one choice of symbol for each state, and the symbols labeling different states are unique.

 
5. A Moore machine operates much like a Markov chain. The machine starts out in one designated start state, transitions stochastically from state to state according to the allowable transitions, and emits the symbol or string of symbols labeling each state when that state is entered. The computation can end only when the machine is in one of the designated final states (although transitions out of final states are permitted), and the result of the computation is taken to be the concatenated labels of the states visited during operation of the machine.

 
6. In general, the more compact models tend to generate larger, less constrained, sets of strings, so if natural selection were to favor either higher-entropy signals or more compact models, one might expect the ultimate outcome to be a species which generates its song by simply emitting syllables entirely at random, without following any grammatical constraints. However, other selective pressures operating simultaneously may prevent the reaching of this extreme condition (as may lack of evolutionary time or insufficient genetic variation), so it is not unreasonable to expect that we may observe a species producing grammatically-constrained song.

 
7. This assumes, of course, that the grammars are learned rather than innate. There are certainly species for which this is not a good assumption, as mentioned above in note 2.

 
8. An alignment between two strings of symbols, or residues, is a representation that explicitly shows the subsequences common to both strings. Short runs of spaces, or gaps, may be inserted into one or both sequences in order to shift portions of the sequence to the left or right in order to maximize the number of matching symbols which are aligned between the two strings and minimize the number of nonmatching symbols which are aligned. A multiple alignment is an alignment between three or more strings, whereas a pairwise alignment includes only two strings.

 
9. The Needleman-Wunsch algorithm utilizes a dynamic programming approach to pairwise alignment by filling in an alignment matrix indicating the cumulative scores of all the different possible partial alignments up to the current position in the two strings. By specifying different parameters, such as the gap open penalty or the mismatch penalty, one can adjust the behavior of the algorithm in various ways to suit the task at hand. Although the Needleman-Wunsch algorithm computes only pairwise alignments, it can be used iteratively to incorporate another sequence into an existing alignment, thereby producing a multiple alignment. This is similar to the popular CLUSTALW program, which first computes a guide tree in order to determine the order in which the pairwise alignments should be performed. Although a guide tree was not used in this study, future work may wish to do so, in order to account for evolutionary relationships between the strings to be aligned.

---

References

[2] Cormen, T. H., C. E. Leiserson, and R. L. Rivest, 1990. Introduction to algorithms. MIT Press, Cambridge, Massachusetts.

[3] Durbin, R., S. Eddy, A. Krogh, and G. Mitchison, 1999. Biological sequence analysis: probabilistic models of proteins and nucleic acids. Cambridge University Press, Cambridge, United Kingdom.

[4] Gold, E. M., 1967. Language identification in the limit. Information and Contro 10:447-474.

[5] Gold, E. M., 1978. Complexity of automaton identification from given data. Information and Control 37:302-320.

[6] Goldberg, D. E., 1989. Genetic algorithms in search, optimization and machine learning. Addison-Wesley, Reading, Massachusetts.

[7] Greene, E., 1999. Toward an evolutionary understanding of song diversity in Oscines. Auk 116:299-301.

[8] Hopcroft, J. E., and J. D. Ullman, 1979. Introduction to automata theory, languages, and computation. Addison-Wesley, Reading, Massachusetts.

[9] Horne, R. S., 1995. Spectrogram version 2.3. <http://www.visualizationsoftware.com/gram.html>.

[10] Lynch, A., and A. J. Baker, 1993. A population memetics approach to cultural evolution in Chaffinch song: meme diversity within populations. American Naturalist 141:597-620.

[11] Margoliash, D., and A. C. Yu, 1996. Temporal hierarchical control of singing in birds. Science 273:1871-1875.

[12] Mundinger, P., 1975. Song dialects and colonization in the House Finch, Carpodacus mexicanus, on the East Coast. Condor77:407-422.

[13] Pitt, L., and M. Warmuth, 1989. The minimum DFA consistency problem cannot be approximated within any polynomial. STOC '89: Proceedings of the Twenty First Annual ACM Symposium on Theory of Computing.

[14] Pytte, C. L., 1997. Song organization of House Finches at the edge of an expanding range. Condor 99:942-954.

[15] Rissanen, J., 1978. Modeling by shortest data description. Automatica 14:465-471.

[16] Smith, A. R., 1996. Cultural evolution in House Finch song. Unpublished honors thesis, Williams College, Williamstown, MA.

[17] SPSS, Inc. SPSS for Windows Release 8.0.0. SPSS, Inc., Chicago, Illinois.

[18] Tracy, T. T., and M. C. Baker, 1999. Geographic variation in syllables of House Finch songs. Auk 116:666-676.

[19] Werner, M., 1998. daVinci V2.1.x online documentation. <http://www.tzi.de/daVinci/docs/>. Universitat Bremen, Bremen, Germany.

[20] Wolff, J. G., 1982. Language acquisition, data compression and generalization. Language and Communication 2:57-89.

[21] Zar, J. H., 1996. Biostatistical Analysis. Prentice Hall, Supper Saddle River, New Jersey.