 Gatherer,
D. (2001). Modelling the effects of memetic taboos on genetic homosexuality.
Gatherer,
D. (2001). Modelling the effects of memetic taboos on genetic homosexuality.
Journal of Memetics - Evolutionary Models of Information Transmission, 4.
http://cfpm.org/jom-emit/2001/vol4/gatherer_d.html
 Gatherer,
D. (2001). Modelling the effects of memetic taboos on genetic homosexuality.
Gatherer,
D. (2001). Modelling the effects of memetic taboos on genetic homosexuality.
Simple computer simulations of the interaction of genetic factors and memetic taboos in human homosexuality, are presented. These simulations clearly show that taboos can be important factors in the incidence of homosexuality under conditions of evolutionary equilibrium, for example states produced by heterozygote advantage. However, frequency-dependent taboos, i.e. taboos that are inversely proportional to the incidence of homosexuality, cannot produce the oscillating effect on gene frequencies predicted by Lynch (1999). Effective oscillation is only produced by rapid withdrawal and re-imposition of taboos in a non-frequency-dependent manner, and only under conditions where the equilibrium incidence of homosexuality is maintained by heterozygote advantage, or other positive selectional mechanism. Withdrawal and re-imposition of taboo under conditions where homosexuality is subject to negative selection pressure, produce only feeble pulses, and actually assist in the extinction of the trait from the population. Additionally it is shown that frequency-dependent taboos assist in a more rapid achievement of equilibrium levels, without oscillation, under conditions of heterozygote advantage. An attempt is made to relate the simulations to past and contemporary social conditions, concluding that it is impossible to decide which model best applies without accurate determination of realistic values for the parameters in the models. Some suggestions for empirical work of this sort are made.Key words: gene-meme co-evolution, homosexuality, memetics
"In a nutshell, ... [the theory]... says that adherents of the taboo out-procreated more tolerant people over the course of many generations in ancient times, leading to increased prevalence of the taboo. (This does not require anything like a perfect correlation between morality and behaviour, or a perfect child inculcation rate, but only enough to increase taboo prevalence by several percent per generation over hundreds of generations.) Then horizontal transmission kicked in as people maligned homosexuality to "prove" their adherence to the taboo. As the taboo becomes extremely widespread, most homosexuals live heterosexual lives, leading them to reproduce any genes involved. As these genes gain prevalence, the rate of taboo dropout increases. Gene carriers who have dropped the taboo are more sexually and socially motivated to spread acceptance of homosexuality than are non-gene carriers who drop the taboo. So the rising gene prevalence can lead to a self-sustained propagation of pro-gay memes. That, in turn, can lead to lower gene prevalence in the next generation, and even lower prevalence of pro-gay memes. All of this leads to potential fluctuations over long time spans." (Lynch 1999)
This paper investigates this hypothesis using a simple model incorporating
Fisher's classic equations of natural selection, upon which is superimposed
a model of a memetic taboo as a restriction on the freedom to openly practice
a homosexual lifestyle. The taboo is assumed to be strictly memetic, i.e.
there is no genetic predisposition to intolerance, and there is no tendency
for individuals of any particular genotype to exhibit one meme as opposed
to another, i.e.. there is no gene-meme linkage disequilibrium (Laland
1992). Various computer simulations were scripted in Perl, and used
to analyse the effects of taboos and heterozygote advantage on the incidence
of genes predisposing to homosexuality. The Perl scripts are available
on http://www.geocities.com/derek_gatherer/supp.htm.
| a) | predisposition to homosexuality is a single-locus, biallelic autosomal recessive; |
| b) | heterozygotes are heterosexual; |
| c) | the homosexual phenotype results in a lower level of sexual reproduction than the heterosexual phenotype; |
| d) | a large population is modelled, in which there is no significant genetic drift, and no immigration of groups with different genetic compositions. |
Following Fisher's classic model of selection against an autosomal recessive
trait (given in Ayala and Kiger 1984), a
hypothetical population can be modelled, in which a/a is the genotype
of individuals predisposed to homosexuality, A/a is the genotype
of heterozygous individuals, and A/A are individuals carrying no
copies of the gene predisposing to homosexuality. A small illustration
follows of the way that selection pressures are calculated in the classic
methodology. Following the tradition in classical genetics, these individuals
A/A
are referred to as the `wild-type', and A as the `wild-type allele'.
H-W is the expected proportion of each genotype under the Hardy-Weinberg
equilibrium.
| A/A | A/a | a/a | |
| H-W |
0.25
|
0.5
|
0.25
|
| Parents |
2500
|
5000
|
2500
|
| Progeny |
7500
|
15000
|
750
|
| Av./indiv |
3
|
3
|
0.3
|
| Fitness |
1
|
1
|
0.1
|
|
|
0
|
0
|
0.9
|
Table 1 shows an illustrative population of 10,000 individuals in an initial Hardy-Weinberg equilibrium. Thus, if q is frequency of the allele a predisposing to homosexuality and p is the frequency of the wild type allele A, and p + q = 1 (i.e. a bialleleic locus), then the frequencies of our phenotypes are:
A/A p2In table 1, q = 0.5, thus the proportions of A/A:A/a:a/a are 1:2:1.A/a 2pq
A/a q2
The population in Table 1 is growing rapidly, purely for illustrative purposes. The frequencies of the progeny in the next generation are counted. (The progeny of each male and female is counted separately, so each offspring is effectively counted twice - this however is of no bearing on the result, as the relative quantities of progeny are the important issue in the calculation of fitness and selective pressure).
In the example in Table 1 A/A and A/a individuals produce an average of 3 progeny each, but a/a individuals only produce 0.3 offspring per individual. Fitness (w) is the relative reproductive success of each genotype compared to the most successful genotype. By this criterion, genotypes A/A and A/a have fitness w = 1, and genotype a/a has fitness w = 0.1.
Selection pressure, s = 1 - w, so for genotype a/a this is 0.9.
One may then proceed to Fisher's model of change in allele frequency per generation for a disadvantageous autosomal recessive trait (given in Ayala and Kiger 1984)
(1)
5 different values of s are chosen ranging from 0.9 down to 0.1.
The results are plotted below (Figure 1):

Figure 1: incidence of homosexuality plotted over 50 generations,
at varying levels of s, from 0.1 to 0.9. s has an effect
on the rate of decrease, but the overall trend is always downwards.
It can be seen that in all cases, the incidence of homosexuality declines. At the highest value of s, 0.9, only 1.5% of the population are homosexual after 10 generations. Even at the relatively mild level of s = 0.1, corresponding to a reproductive deficiency of only 10% per generation, 10 generations produces a decline in homosexuality from 90% of the population to 78.4%.
It is thus clear that if homosexuality is due to recessive genetic factors, and if homosexuals are less successful at sexual reproduction than heterosexuals, (i.e. if s > 0, even by a small value), homosexuality will eventually disappear from the population (except for new mutations). This disappearance can be astonishingly rapid, e.g. at s = 0.9 homosexuality falls from 90% of the population to 23% in a mere 3 generations.
b = 1- (hvis/htotal)where hvis are `visible' homosexuals, leading openly homosexual lives and htotal is the total number of predisposed homosexuals of genotype a/a.
It is assumed that those individuals of genotype a/a who lead heterosexual lives have rates of sexual reproduction equal to individuals of genotypes A/A and A/a.
Therefore b reduces s as follows:
stab = s(1-b)where stab is the selection pressure in the presence of taboo b, and s is the selection pressure in the absence of any taboo.
stab can then be substituted for s in equation (1) above.
Which can also be reexpressed using Laland's (1992) nomenclature, as:
(2)where there are two cultural traits, r1 and r2, and only the phenogenotype a/a. r2 is deleterious.
b is kept constant by requiring that Laland's (1992) expression for the horizontal transmission of a meme within a single generation, result in no change, i.e.. that Nd(i) should always equal Nd(i-1):
(3)where Ne is the total population, N0 is the initial population exhibiting the meme, Nd(i) is the population exhibiting the meme after i cultural generations (and there are i cultural generations per biological generation), and a is the rate at which the meme tends to be replicated horizontally within that cultural generation. Ne and N0 can be assumed to be constants for the present purposes, so the crucial variables are i, which is arbitrarily set at 1, and a. Therefore simply by adjusting a, the taboo, b, can be kept constant within the population. Adjustments in which b is allowed to change owing to changing values of a, are of course, possible. However, b is kept constant again here for the purposes of simplicity.
Let s and b both be 0.9. Let the initial frequency of
individuals of genotype a/a be 0.9 (again an absurdly high starting
value is taken for the purposes of illustration).

As can be seen, under conditions of taboo of 0.9 the number of visible homosexuals in the population is initially only 9%. The frequency of visible homosexuality, and of predisposed individuals a/a, falls. After 28 generations the number of visible homosexuals has fallen to 4.5% Under such circumstances, it can be seen that taboos alone cannot act to increase or even maintain levels of homosexuality, but can only slow the rate at which it decreases (as is generally predicted for any situation of this kind by Laland 1992, Figure 2 of that article).
Lynch (1999) states "As the taboo becomes extremely widespread, most homosexuals live heterosexual lives, leading them to reproduce any genes involved. As these genes gain prevalence...". It can be seen from the above simulation that this is impossible. A taboo of 0.9 has been chosen, and yet genes predisposing to homosexuality still decrease rapidly. They certainly do not `gain prevalence'.
This situation is produced by again manipulating Laland's equation
(3) above; such that a is alternately extremely high for the
taboo, then extremely high for the non-taboo in 3-generational blocks.
Why a might vary in such a way is irrelevant to present purposes.
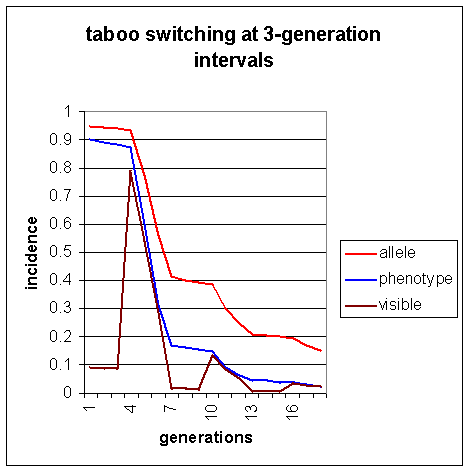
The withdrawal and imposition of the taboo in 3-generation cycles produces a faster overall decline than when the taboo is constant at 0.9. Compare Figure 2 in simulation 2, where s = 0.9, b = 0.9, in which the same interval of 12 generations only produces a decline is visible homosexuality from 9% to 7.7%, with Figure 3 above, in which the withdrawal and reintroduction of the taboo every 3rd generation produces a reduction in 12 generations from 9% to 5.4%
Whenever the taboo is withdrawn, as in generations 4 and 10, there is an increase in visible homosexuality. However, the second sudden increase is much lighter than the first, and further pulses of this sort, such as that caused by the release of the taboo in generation 16, are scarcely visible.
Again following Fisher (as reproduced in Ayala and Kiger 1984), it is possible to produce an equation for the change in allele frequency in the case of heterozygote advantage. In this situation, there is a selection pressure against a/a, s as before, but also a selection pressure t against wild-type homozygotes A/A.
(4)Under such conditions, an equilibrium level is achieved at:
(5)Let s be 0.9 as before.
Let t be 0.1 This means that wild-type homozygotes A/A have a reproductive or survival deficit of 10% relative to heterozygotes.
Let the taboo, b = 0.9.
Let the initial frequency of homosexuality in this case be 0.1.
Let these conditions apply for 150 generations, after which the taboo
decreases to b = 0.5 (again by manipulating the variable a
in Laland's equation (3) above to suit our purposes)
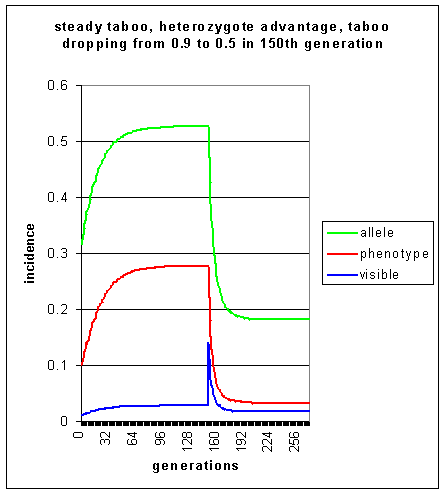
This population initially has a level of visible homosexuality of 1%, but the heterozygote advantage allows this to increase to 2.8% over 95 generations. This is virtually an equilibrium level, which is sustained for a further 55 generations. When the taboo is suddenly diminished after 150 generations, the level of visible homosexuality peaks suddenly to 14% of the population. However, with b now at 0.5, stab is now 0.45. The population begins to move towards a new equilibrium level of visible homosexuality of approx 1.7% achieved after a further 43 or so generations.
Heterozygote advantage thus allows homosexuality to achieve equilibrium levels, whereas simulations 1-3 above all result in downward trends. As was pointed out before in simulation 2, this result is textbook material for geneticists. However, it is included here in order that non-genetical readers may clearly see the effects of heterozygote advantage on a deleterious allele.
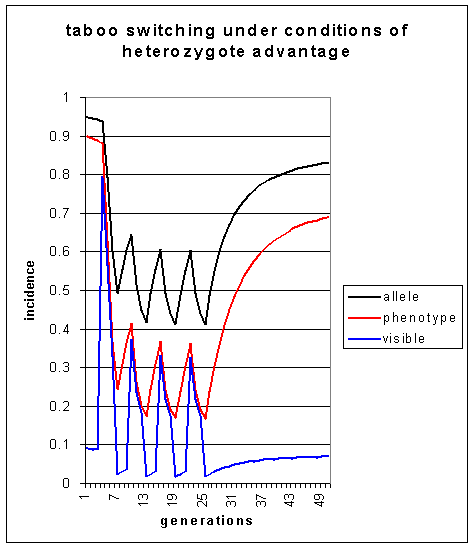
Again the alternating release and reimposition of the taboo cause pulses in the level of visible homosexuality These pulses are much stronger than when there is no heterozygote advantage (see simulation 3), and when the taboo is permanently reapplied, the level of visible homosexuality stabilises at around 7% in the 50th or so generation. Only an excessively implausible level of heterozygote advantage, at t = 0.5, can produce such a striking effect.
Therefore in each generation, the frequency dependent taboo bfd
bfd = 1-q2and the selection pressure, sfd is then
sfd = sinit (1-bfd)where sinit is the selection pressure in the absence of a frequency-dependent taboo.
Let us compare 2 populations, both starting with incidences of homosexuality
of 0.9, and starting with s = 0.9, but one population having a steady
taboo of 0.9, and the other exhibiting a frequency-dependent taboo, where
the bfd changes in each generation as above.
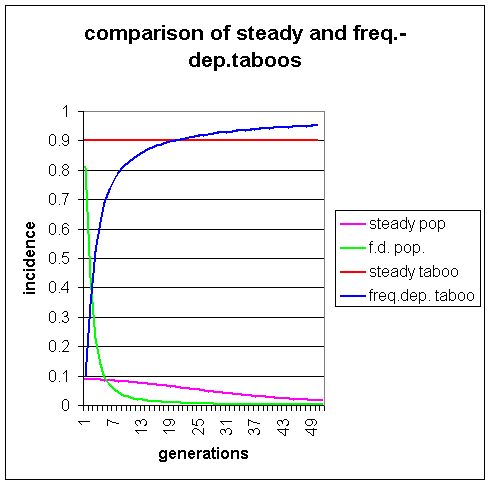
The steady taboo population has a slow decrease in the levels of visible homosexuality from 9% to 4.5% in 23 generations. The frequency-dependent taboo population initially has high levels of visible homosexuality and consequently a low taboo. However, as levels of visible homosexuality drop dramatically under the influence of s = 0.9 in the absence of heterozygote advantage, the taboo climbs, and in generation 20 exceeds the level in population 1. Such high levels of taboo, achieving 0.95 by generation 48, means that visible homosexuality is virtually eliminated from population 2. This shows that frequency-dependent taboos do not produce the oscillating effect that Lynch (1999) claims. On the contrary, a taboo of this sort would speed the eventual elimination of the genes predisposing to homosexuality from the population.
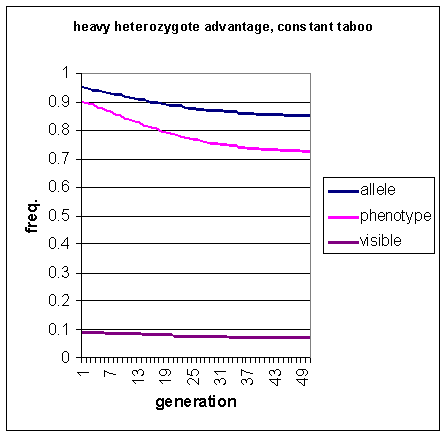
Figure 7: Incidence of allele predisposing to homosexuality,
the homosexually-disposed phenotype and visible homosexuality, under conditions
of heterozygote advantage, over 50 generations. The taboo is constant.
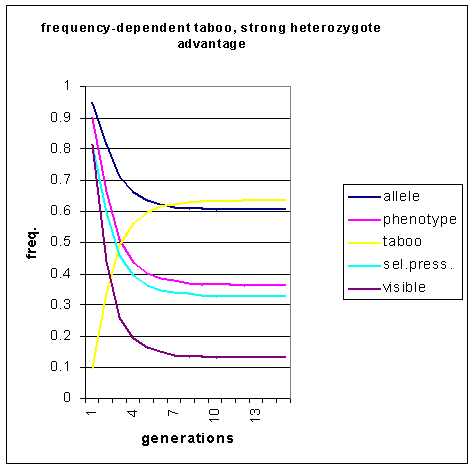
Figure 8: Incidence of allele predisposing to homosexuality,
the homosexually-disposed phenotype and visible homosexuality under conditions
of heterozygote advantage over 15 generations. The taboo is frequency-dependent.
The population with the frequency -dependent taboo rapidly achieves an equilibrium level after only 12 generations, whereas the population with constant taboo takes 50 generations. Note that there are no pulses in the frequency of visible homosexuality. This demonstrates that neither constant nor frequency-dependent taboos can produce the oscillating effect predicted by Lynch (1999).
The fundamental assumption of this paper is that the predisposition to homosexuality is primarily genetic, but that the behavioural expression of that predisposition is determined by memetic factors such as taboos. These models therefore only represent a limited subset of possible models. For instance once might construct a model in which homosexuality is entirely culturally determined, or in which homosexuality is related to environmental factors which are neither genetic nor cultural. Nevertheless, there are compelling reasons to suggest that the gene-meme interactionist approach is at least plausible, given the weight of empirical research that has accumulated on the biological basis of homosexuality and on how cultural attitudes affect it.
Exact quantification of the incidence of male homosexuality in the past and present is a highly controversial area (Gonsiorek et al 1985, Lhomond 1993; Weinrich et al 1993), but an estimate of a current incidence of visible homosexuality of some 5% seems not unreasonable (Johnson 1994). Waugh et al (2000)'s intriguing `lost letter' experiment suggests that the general public are only 49% as likely to behave altruistically to an overtly homosexual as to a non-homosexual person, which means that one might measure taboos accordingly. This would bring the score of a/a individuals up to 10% of the population which is still within some of the upper-end estimates (e.g. Thin and Smith 1976). It is clear that visible homosexuality has recently increased, at least in Western (post)-industrialised societies. Downey (1980) surveyed over 5 generations, and concluded that homosexuality has increased overall among males but that it has decreased among married males, over this time. The decrease in the number of married homosexual males is strongly suggestive of a decrease in taboo. However, the overall increase may suggest that there has also been an actual increase in the frequency of a/a, perhaps due to a heterozygote advantage in the process of achieving equilibrium (e.g. simulation 4). It is possible that the release of previous taboos has been superimposed onto this. If taboos are frequency-dependent (Lynch 1999), then an increase in numbers of a/a individuals due to sex-specific advantage, or a heterozygote advantage in the process of achieving equilibrium, would also trigger decrease in the taboo.
It is clear from the simulations presented here that frequency-dependent taboos do not result in the oscillations predicted by Lynch (1999). By contrast, oscillations can only be produced by imposition and release of frequency-independent taboos, and even then only when phenomena such as heterozygote advantage or sex-specific selection are also operating.
Despite the difficulty of disentangling genetic and cultural factors in the short-term, it may be possible to gather some empirical facts that might help in choosing the most likely model. The models for heterozygote advantage and sex-specific advantage (the latter not explicitly discussed here, but see Ruse 1981; Gallup and Suarez 1983; Dickemann M 1995; Miller 2000) require a fairly extreme set of parameters in order for them to be able to sustain high levels of homosexuality in populations. In the case of the heterozygote advantage model presented here, A/a individuals should have a greater reproductive success. A/a individuals represent two-thirds of the siblings of a/a individuals. If the current level of homosexuality is approximately 10%, i.e. q2 = 0.1 (Thin and Smith 1976), and homosexuals have currently half the level of reproductive success of heterosexual males, i.e. s = 0.5 (this is pure conjecture - this parameter is one which needs empirical research), then the heterozygote equilibrium equation (equation 5, above):
trivially solves to:
t = 0.24Therefore, if the above estimates for q and s are correct, one requires t = 0.24 to sustain this in a system of heterozygote advantage. This implies that the A/a siblings of homosexuals have a strong reproductive/survival advantage over wild-type A/A individuals, of some 24%. The magnitude of the required t is therefore scarcely plausible, and one might be tempted to exclude the heterozygote advantage hypothesis on this basis. However, empirical data is need to ascertain if the above estimates for q and (especially) s are accurate. The 1994 National Survey of Sexual Attitudes and Lifestyle (Johnson 1994) estimated the incidence of homosexuality to be between 1.1% and 6.4% of men and 0.4% and 3.4% of women. If the most conservative estimate of 1.1% is taken, then t under heterozygote advantage where s remains 0.5, becomes (0.10 x 0.5)/0.9 = 0.06, which is perhaps a more plausible value. If s is overestimated, then t reduces even further.
A 1970 survey (Fay et al 1989) placed the level of homosexual contact in the previous 12 month period as being some 1.6 to 2.0% of males. This gives an upper bound to q of 0.14. Furthermore, half of these males were found to be `currently or previously married'. If we assume these males to have been equally reproductive as heterosexual men within their marriages, and if we assume never-married homosexual males to be non-reproductive, then we have s = 0.5. If we assume that non-reproductive homosexuality is predominantly male in its expression, then s reduces further to 0.25. We can then estimate t at (0.14 x 0.25)/0.86 = 0.04. Heterozygote advantage need only be 4% if these values are accurate.
Furthermore, it is clear that although heterozygote advantage can (at least theoretically) sustain levels of homosexuality, and female-specific selection is even capable of increasing it, both of these mechanisms are unstable and vulnerable to sudden fluctuations in taboo (but not to frequency-dependent taboos). It is also clear that taboos alone in the absence of a positive selective mechanism such as heterozygote advantage, are insufficient to account for oscillating patterns in visible homosexuality. For instance compare simulations 2 and 3 with simulation 5. Simulation 5 has a strong oscillation only because there is also strong heterozygote advantage in the system.
One must be careful to distinguish current selective pressures from those operating in the past. It is possible that genes predisposing to homosexuality were elevated in the past through heterozygote advantage or female-specific selection, but that those selective pressures no longer apply. Therefore genes predisposing to homosexuality would now be in the model described in simulation 1, and be in a steady decline. The apparent 20th century increase in visible homosexuality (Downey 1980) might just be a blip caused by a release in a taboo, which will be followed by a greater decrease in future generations. Alternatively, there may be selective mechanisms, such as heterozygote advantage or female-specific selection which are still in operation.
In summary, it is not possible to make accurate predictions concerning the application of these models to the real world without data concerning the reproductive success of siblings of homosexual males, and indeed of homosexuals themselves. If such data could be obtained, an estimate could be made for the parameters of the heterozygote advantage and female-specific advantage models. If either of these models is found to be plausible in view of this empirical data, estimates could be made for future levels of homosexuality subject to any fluctuations caused by changes in taboo which, as shown, are at their most important when strong biological selection is occurring.
If the empirical data does not support either of the strong selection models above, it must be concluded that visible homosexuality will decline. On the other hand, it may be that gene-meme interaction models of the sort presented here, miss some crucial environmental, psychological or sociological element that can explain why homosexuality is maintained even when gene-meme analysis might suggest it should not be.
Ayala FJ and Kiger JA (1984) Modern Genetics 2nd ed. Benjamin/Cummings, Menlo Park.
Bailey JM and Pillard RC (1991) A genetic study of male sexual orientation. Arch. Gen. Psychiat. 48, 1089-1096.
Bailey JM and Benishay DS (1993) Familial aggregation of female sexual orientation. Am. J. Psychiat. 150, 272-277.
Bailey JM, Pillard RC, Neale MC and Agyei Y (1993) Heritable factors influence sexual orientation in women. Arch. Gen. Psychiat. 50, 217-223.
Diamond JM (1988) Tay-Sachs carriers and tuberculosis resistance. Nature 331, 666.
Dickemann M (1995) Wilson's Panchreston: the inclusive fitness hypothesis of sociobiology re-examined. J. Homosex.28, 147-183.
Downey L (1980) Intergenerational change in sex behavior: a belated look at Kinsey's males. Arch Sex Behav 9, 267-317.
Durham WH (1991) Coevolution: genes, culture and human diversity. Stanford University Press, Stanford.
Fay RE, Turner CF, Klassen AD and Gagnon JH (1989) Prevalence and patterns of same-gender sexual contact among men. Science243, 338-48.
Gabriel SE, Brigman KN, Koller BH, Boucher RC and Stutts MJ (1994) Cystic fibrosis heterozygote resistance to cholera toxin in cystic fibrosis mouse model. Science 266, 107-109.
Gallup GG and Suarez SD (1983) Homosexuality as a by-product of selection for optimal heterosexual strategies. Perspect Biol Med 26, 315-22.
Gonsiorek JC, Sell RL, Weinrich JD (1995) Definition and measurement of sexual orientation. Suicide Life Threat Behav 25 Suppl, 40-51.
Hamer DH, Hu S, Magnuson VL, Hu N and Pattatucci AML (1993) A linkage between DNA markers on the X chromosome and male sexual orientation. Science 261, 321-327.
Hu S, Pattatucci AML, Patterson C, Li L, Fulker DW, Cherny SS, Kruglyak L and Hamer DH (1995) Linkage between sexual orientation and chromosome Xq28 in males but not in females. Nature Genet. 11, 248-256.
Haynes JD (1995) A critique of the possibility of genetic inheritance of homosexual orientation. J Homosex 28, 91-113.
Johnson AM (1994) (ed.) Sexual attitudes and lifestyles. Blackwell Scientific Publications, Oxford.
Laland KN (1992) A theoretical investigation of the role of social transmission in evolution. Ethology and Sociobiology 13, 87-113.
LeVay, S (1991) A difference in hypothalamic structure between heterosexual and homosexual men. Science 253, 1034-1037.
Lhomond B (1993) Between man and woman: the character of the lesbian. J Homosex 25, 63-73.
Lynch A (1999) Thought Contagion: How Belief Spreads through Society. A response to Paul Marsden. Journal of Artifical Societies and Social Simulation 2 (http://jasss.soc.surrey.ac.uk/2/3/lynch.html).
McFadden D and Pasanen EG (1999) Spontaneous otoacoustic emissions in heterosexuals, homosexuals, and bisexuals. J Acoust Soc Am 105, 2403-13.
Miller EM (2000) Homosexuality, birth order, and evolution: toward an equilibrium reproductive economics of homosexuality. Arch Sex Behav 29, 1-34.
Pillard RC and Weinrich JD (1986) Evidence of familial nature of male homosexuality. Arch. Gen. Psychiat.43, 808-812.
Reite M, Sheeder J, Richardson D and Teale P (1995) Cerebral laterality in homosexual males: preliminary communication using magnetoencephalography. Arch Sex Behav 24, 585-93.
Rice G, Anderson C, Risch N and Ebers G (1999) Male homosexuality: absence of linkage to microsatellite markers at Xq28. Science284, 665-667.
Risch N, Squires-Wheeler E and Keats BJB (1993) Male sexual orientation and genetic evidence. Science 262, 2063-2065.
Ruse M (1981) Are there gay genes? Sociobiology and homosexuality. J Homosex 6, 5-34.
Sanders G and Wright M (1997) Sexual orientation differences in cerebral asymmetry and in the performance of sexually dimorphic cognitive and motor tasks. Arch Sex Behav 26, 463-80.
Snyder PJ, Weinrich JD and Pillard RC (1994) Personality and lipid level differences associated with homosexual and bisexual identity in men. Arch Sex Behav 23, 433-51.
Spyropoulos B, Moens PB, Davidson J and Lowden JA (1981) Heterozygote advantage in Tay-Sachs carriers?. Am. J. Hum. Genet. 32, 375-380.
Swaab DF and Hofman MA (1995) Sexual differentiation of the human hypothalamus in relation to gender and sexual orientation. Trends Neurosci18, 264-70.
Thin RN and Smith DM (1976) Some characteristics of homosexual men. Br J Vener Dis 52, 161-4.
Waugh IM, Plake EV and Rienzi BM (2000) Assessing attitudes toward gay marriage among selected Christian groups using the lost-letter technique.Psychol Rep 86, 215-8.
Weinrich JD, Snyder PJ, Pillard RC, Grant I, Jacobson DL, Robinson SR and McCutchan JA (1993) A factor analysis of the Klein sexual orientation grid in two disparate samples. Arch Sex Behav 22, 157-68 .
Werner D (1979) A cross-cultural perspective on theory and research on male homosexuality. J Homosex 4, 345-62.
Woolf LI (1986) The heterozygote advantage in phenylketonuria. Am. J. Hum. Genet. 38, 773-775.
Zhou JN, Hofman MA, Gooren LJ and Swaab DF (1995)
A sex difference in the human brain and its relation to transsexuality.
Nature378,
68-70.