Kendal, J. R. and Laland, K. N. (2000). Mathematical Models for Memetics.
Journal of Memetics - Evolutionary Models of Information Transmission, 4.
http://cfpm.org/jom-emit/2000/vol4/kendal_jr&laland_kn.html

Abstract

1 - Introduction
2 - Introducing an Established Modelling Paradigm
3 - Imitate the Imitators
4 - Conclusions

Abstract

The science of memetics aims to understand the evolution of socially transmitted cultural traits. Recently attention has focused on the interaction between memetic and genetic evolution, a phenomenon described as meme-gene co-evolution. Whether cultural evolution occurs purely at the level of the meme, or through meme-gene interaction, a body of formal theoretical work already exists that can be readily employed to model empirical data and test theoretical hypotheses. This is cultural evolution and gene-culture co-evolutionary theory, a branch of theoretical population genetics (Cavalli-Sforza & Feldman [6]; Boyd & Richerson [3]; Feldman & Laland [12]). We reject the argument that meaningful differences exist between memetics and these population genetics methods. The goal of this article is to point out the similarities between memetics and cultural evolution and gene-culture co-evolutionary theory, and to illustrate the potential utility of the models to memetics. We illustrate how the theory can be applied by developing a simple illustrative model to test a hypothesis from the memetics literature.

Keywords: brain size, cultural evolution, gene-culture co-evolution, meme, memetics

1 Introduction

We begin by pointing to the similarities between memetics and cultural evolution theory. Both disciplines explicitly assume that at least some aspects of human culture can be broken down into discrete traits, or component elements, henceforth memes (although both approaches have also explored the evolution of continuous traits). Both disciplines believe that memes can increase or decrease in frequency through the processes of Darwinian evolution (i.e., the differential survival and reproduction of individuals), as well as through similar or analogous processes affecting cultural selection (i.e., the differential survival and reproduction of memes). Both disciplines stress that memes should be treated as replicators in their own right, and most proponents of each would probably accept that the adoption of at least some memes is not independent of the individual's genotype. We suspect that most advocates of the population genetics approach would be sympathetic to the argument that many of the dynamics of contemporary human culture are best understood at the level of the meme. The allocation of parameters to describe rates of cultural transmission in cultural evolution and gene-culture co-evolution models is formally equivalent to treating cultural transmission based on cultural replicators that are distinct from genes (Feldman & Cavalli-Sforza [10]; Cavalli-Sforza & Feldman [6]). We also suspect that many memeticists would be sympathetic to Feldman & Laland's [12] claim that much human evolution over the last 2 million years can be best understood as gene-culture (or meme-gene) co-evolution. Indeed the basic philosophy and parallels between the two approaches are so similar, it is striking that they have not converged.

We suggest that there are two main reasons why memetics has not yet embraced cultural evolution, neither of which is of sufficient validity to warrant their continued divergence. The first reason is that cultural evolution and gene-culture co-evolutionary theory are relatively small and specialized branches of population genetics, with a lot of the research published in highly-rated yet somewhat esoteric journals, and containing material of an extremely technical and mathematical nature, but which rarely adopts the term meme, or refers to the memetics literature. As a result of this, many meme enthusiasts are simply unaware of this population genetics literature, and among those that are, many find it difficult to comprehend. This article is written with the belief that these technicalities and linguistic differences should not be allowed to drive a wedge between two disciplines that otherwise have such similar goals, and for which the opportunities for cross-fertilisation of ideas and methods are considerable. It is quite clear that memetics as a discipline is not at all hostile to theory, and that many meme enthusiasts are sufficiently mathematically sophisticated to understand the theoretical papers. One of the goals of this paper is to introduce cultural evolution methods to a memetics audience.

A second reason why memetics has distanced itself from cultural evolution theory is the belief among meme enthusiasts that advocates of cultural evolutionary theory assume genes or genotypes to control the adoption and transmission of memes. To use Lumsden and Wilson's [17] metaphor, memeticists think that cultural evolutionists believe memes are on a genetic leash. This is not the case. Although Lumsden and Wilson used the terms cultural evolution and gene-culture co-evolution, their work had more in common with the earlier sociobiologists than with modern cultural evolution and gene-culture co-evolutionary theory. The population genetics approach to culture grew out of a rejection of sociobiology. This rejection stems, in part, from sociobiology's failure to take cultural transmission seriously, or to recognise that not all cultural traits are to the ultimate benefit of the genes. Cultural evolution and gene-culture co-evolutionary models have developed a system of formalism that allows for leashes of variable length, ranging from extremely tight genetic control, to no meaningful genetic influence at all (see Feldman & Laland [9], for a discussion of this issue). The models do this by allocating parameters that determine the probability that an individual will acquire a particular meme that may, or may not, differ according to the individual's genotype. Moreover, gene-culture co-evolutionary theory has long explicitly asserted that the leash tugs both ways, and that under some circumstances genes can be under cultural control (Feldman & Cavalli-Sforza [10]; Feldman & Laland [9]). If contemporary practitioners of gene-culture co-evolutionary theory no longer ask Dennett's [7] Cui bono? question, it is because two decades earlier they developed their own method of answering this question, namely, the phenogenotype. We describe how phenogenotypes can be used to explore meme-gene co-evolution below. For the moment it is sufficient to note that there is nothing in cultural evolution theory that precludes cultural adaptations "for the good of the meme", or a "meme's-eye-view" approach.

We reject the argument that meaningful differences exist between memetics and the population genetics methods. We also believe that cultural evolution and gene-culture co-evolutionary theory will be much enriched by embracing memetics. Prima facie complex social phenomena, for example, institutions or belief systems, may be treated as memeplexes made up of a plethora of attributes, many of which are memes in their own right, each with varying distribution and dynamics (Plotkin [18]; Blackmore [2]). Social anthropologists limit their ability to carry out predictive and comparative analyses, by insisting on an all-encompassing, holistic approach, rather than breaking culture down into manageable units, and performing rigorous quantitative analyses. We do not refute the idea that the distributions of cultural traits may be complex, but suggest that real progress can be made by addressing those cultural traits that have manageable, easily identified and quantifiable distributions. In the case of our worked example, imitate the imitators, we are interested in the presence or absence of a particular cultural trait, therefore it is appropriate to consider discrete memes. Part of the excitement generated by the memetics movement surely reflects the fact that the meme concept by its very existence operationalises culture, breaking it down into the kind of discrete packages that can be subject to scientific enquiry. We believe that mathematical analyses, using cultural evolution and gene-culture co-evolutionary models, can be profitably employed in restricted domains, where cultural traits or memes are easily defined and quantitative studies are possible. We suggest that the techniques of cultural evolution and gene-culture co-evolution can be employed to describe and predict how cultures change, explain current trends in cultural attributes, and test hypotheses concerning the evolution of human behaviour and culture.
 

2 Introducing an Established Modelling Paradigm

Population geneticists recognise that a salient model should be developed at the level of the smallest non-divisible unit, as this is the natural currency by which changes in replicator frequency will occur. For illustration, imagine the co-evolution of two genetic loci subject to natural selection in a population of animals. We will call the loci A (with alleles A and a) and B (with alleles B and b). A two-locus population genetics model would have to track the frequencies of each of the four types of chromosomal combination (AB, Ab, aB, and ab), usually describing them as gametes. The two loci cannot be assumed to be independent because there may be complex interactions or non-random associations between loci, depending on the nature of the selective regime. Subsequent analysis of the system will tell us whether allele A is favoured over allele a, and describe the evolution at the B locus. The same applies to gene-culture co-evolution, except here one of the loci (say B) contains variants of meme (meme variants B and b) rather than alleles of a gene. The (rather cumbersome) name given to particular combinations of genotype and meme is the phenogenotype. In population genetics models, the genotypes are allocated fitnesses and the rate of transmission is tracked using recursions which describe the frequency of each genotype in terms of the frequencies of genotypes in the previous generation. Likewise, for the gene-culture co-evolutionary model, each phenogenotype is allocated a "fitness", representing its rate of reproduction. However, while genes are transmitted to each individual once a generation, meme transmission is more complex, and may occur on a within-generational timeframe, depending on who acquires the meme from whom. Nonetheless, it is frequently mathematically convenient to track rates of change of phenogenotypes using a generational timeframe. Of course, individuals change their memes frequently throughout their lifetimes, and this will be reflected in changing frequencies of phenogenotypes. In tracing the fortunes of the meme, the model only makes assumptions as to the path of transmission and not the processes that underlie replication. As long as the meme is observable and measurable, analysis of the dynamics of the system can be used in conjunction with empirical data to question the nature of these assumptions, explore the replication process, and test predictions. While there may be nothing directly equivalent to a `locus' or `allele' for memes, we believe that sufficient memes compete directly with each other for this to be a useful abstraction.

The gene-culture co-evolutionary framework embraces the full range of selective influences upon the evolution of memes: memetic fitness may be quite independent of genetic influence (there is no genetic leash); memes may influence the fitness of genes (genes are held on a memetic leash); or genetic fitness can determine the success of the meme (memes are held on a genetic leash). For purposes of exposition, we introduce the use of the gene-culture co-evolutionary methods under each of these circumstances.

If cultural inheritance is completely independent of genetic inheritance, that is, if memes are acquired independently of the learner's genotype, then the unit of cultural selection collapses to that of the meme. Under such circumstances, tracking gene frequencies is of no value, gene-culture co-evolutionary methods are inappropriate, and all evolution occurs at the level of the meme. It is here that cultural evolution methods are useful. Cultural evolutionary theory is a modelling paradigm developed by Cavalli-Sforza & Feldman and others to analyse cultural change (Feldman & Cavalli-Sforza [10]; Cavalli-Sforza & Feldman [6]; Boyd & Richerson [3]). This framework has been used to explore phenomena as diverse as linguistics, epidemics, social values and customs, and the diffusion of innovations (i.e. the same subject matter as memetics). Cultural evolutionary models do not use the term meme because they were first developed prior to the publication of The Selfish Gene. Instead they use the phrase "cultural trait" or "cultural phenotype". Nonetheless, Cavalli-Sforza and Feldman's methods effectively track changes in meme frequency in a population through cycles of mating, differential social transmission of the meme (cultural selection) and natural selection. The modes of social transmission describe the routes by which memes spread (Cavalli-Sforza & Feldman [6]). Social transmission can occur vertically (from parents to offspring), obliquely (from parental to offspring generation) or horizontally (within generation transmission), or some combination of these.

Cavalli-Sforza & Feldman define cultural selection as a Darwinian process by which particular memes increase or decrease in frequency due to their differential probability of being adopted by other individuals. In contrast, for these authors natural selection refers to the differential survival of individuals expressing different types of memes. For instance, the spread of contraceptive use through cultural selection processes could alter natural selection pressures induced by sexually transmitted diseases. Therefore the analysis is based on the explicit assumption that cultural traits evolve by Darwinian selection processes, whereby individuals can be selected purely on the basis of their memes. This allows interesting questions to be asked such as, 'Under what conditions might non-adaptive cultural traits evolve?', (Cavalli-Sforza & Feldman [6]). One of the earliest findings to emerge from this analysis is that there are countless circumstances when memes with sufficiently high cultural fitness can increase in frequency despite being maladaptive from a genetic perspective, and decreasing genetic fitness (Feldman & Cavalli-Sforza [10]). Cavalli-Sforza and Feldman's framework also considers cases in which cultural selection operates without affecting Darwinian fitness (e.g. a preference for a particular soft drink).

The models' strengths are in their simple formalization, the ability to predict the frequencies of cultural traits, and the direct applicability to empirically derived transmission coefficients. Cavalli-Sforza and Feldman [6] demonstrated that models can be applied to empirical data, estimating the transmission coefficients for five vertically transmitted traits that would be of interest to meme enthusiasts: salt usage, frequency of praying to God, frequency of swimming, belief in ability versus luck, and political interest. The models can be used to describe patterns of change, make sense of meme variation, extrapolate back into the past to predict past cultural usage, and extrapolate into the future to predict future trends. We have only begun to describe the breadth of cultural evolution models, and countless elaborations and refinements of the methods have emerged, for example, investigating frequency-dependent transmission, the evolution of continuous (quantitative) traits, and the effects of migration, population structure, innovation, and other factors (Cavalli-Sforza & Feldman[6]; Boyd & Richerson[3]; see Laland[15] for a simple introduction).

There are also situations where there is an interaction between memes and genes, such that an individual's propensity to adopt a particular meme depends on his or her genotype. This is likely to be more common in investigations of human evolution than in explorations of contemporary human culture. Under such circumstances where there may be meme-gene co-evolution, gene-culture co-evolutionary methods are appropriate. For example, Feldman and Cavalli-Sforza [11] used gene-culture co-evolutionary theory to investigate the evolution of lactose absorption. By defining genotypes that differ in terms of their ability to process lactose, and by describing individuals as either having a meme for milk consumption or not, Feldman and Cavalli-Sforza were able to develop a population genetics model to explore how dairy farming and milk use might co-evolve with genes for lactose absorption. In this case, the cultural trait is treated as a discrete meme (milk user or nonuser), rather than as a continuous distribution, which simplifies the model without compromising the qualitative results. The analysis suggested that whether or not the allele for absorption achieves a high frequency depends critically on the probability that the children of milk users themselves adopt the meme. The analysis is able to account for both the spread of lactose absorption, and the culturally related variability in its incidence. Moreover, Feldman & Cavalli-Sforza found a broad range of conditions under which the absorption allele does not spread despite a significant fitness advantage. Meme transmission complicates the selection process to the extent that the outcome may differ from that expected under purely genetic transmission.

In the lactose absorption example, the leash tugs both ways: whether or not an individual drinks milk depends on his or her genotype, but also whether or not the genes for lactose absorption are present in a population depends on the history of dairy farming in that culture. Such two-way influences are likely to have been common throughout recent human evolution, and may have been particularly important in the evolution of the human brain. A number of theories have related the change in brain size and associated anatomical effects with cultural change (Humphrey [14]; Holloway [13]; Wilson [20]; Byrne & Whiten [5]; Dunbar [8]; Aiello & Wheeler [1]). For example, the evolution of the brain with a costly, high mass specific, metabolic rate may have been paid for by a reduction in the size of the gastro-intestinal tract (Aiello & Wheeler [1]). Aiello and Wheeler [1] suggested that a reduction in gut size was only possible because the larger brains were capable of culturally mediated improvement in diet, in proportion to the loss of gut. Humphrey [15] emphasised the effect of social behaviour and hierarchy upon the evolution of brain size, resulting in the acceleration of cultural evolution. Wilson et al. [20] suggested the behavioural drive hypothesis, predicting that the dual capacity for behavioural innovation and social propagation of new habits accelerated anatomical evolution. Gene-culture co-evolutionary theory is suited to investigate the plausibility of such hypotheses.

One recent interesting addition to hypotheses concerned with brain evolution has been made by Blackmore [2]. Blackmore suggests that social learning and memetic drive are the cause behind the evolution of increased brain size, proposing a three stage process. Firstly, individuals with a predisposition for imitating (we will call them 'generalist' imitators, as they are not biased to learn from any particular individual) would succeed over those that only learn directly from the environment. Secondly, in a population of imitators, those with a predisposition to imitate from the best imitators would be selected (we will call them 'selective' imitators). Thirdly, preferential mating between enhanced imitators would produce the most successful offspring. The selective imitators are assumed to require a greater than average cognitive capacity, therefore there is selection for an increase in the average brain size. As this hypothesis comes directly from the memetics literature, in order to illustrate the gene-culture co-evolutionary method we show how one aspect of Blackmore's hypothesis can be tested using a phenogenotype model.
 

3 Imitate the Imitators

Genotype Meme	II	Ii	ii
B1
B0			1

After random mating with respect to the two memes and two genotypes, the B₁ meme is passed down from the parental generation to the offspring generation in a manor dependent on its genotype (see Table 2).

Genotype	II	Ii	ii
Probability of B1	p1=	p2=	p3=

The probability that an individual acquires the B₁ phenotype depends upon its genotype, on the probability of social learning, c and the frequencies of B₁ individuals of the parental generation. Whereas generalist imitators can potentially learn from all B₁ individuals in the parental generation, selective imitators constrain themselves to copying the sub-population of selective imitators in the parental generation. In either case, the probability of adopting the B₁ meme is directly proportional to its frequency in the relevant population.

Using the assumptions in tables 1 and 2, we can construct recursions defining the relationship between the frequencies of each phenogenotype in the parental and offspring generations. In each offspring generation, phenogenotype frequencies depend upon the probability of acquiring the genotype following random mating in the parental generation, the probability of acquiring the particular phenotype given the genotype (Table 2), and the fitness associated with the phenogenotype in question (Table 1). In this case, the system can be reduced from six phenogenotype recursions to a simpler system, with the following set of four recursions (1a-d). These recursions give the frequency of the I and i alleles in individuals with B₁ and B₀ memes, respectively.

(1a)
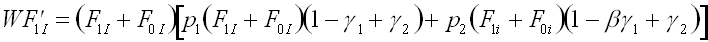
(1b)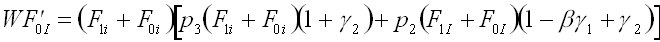
(1c)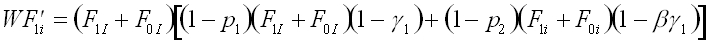
(1d)

Analysing this mathematical system [note 2] reveals that whether selective imitators evolve in a population of generalist imitators depends on whether the following inequality is satisfied, namely

(2).

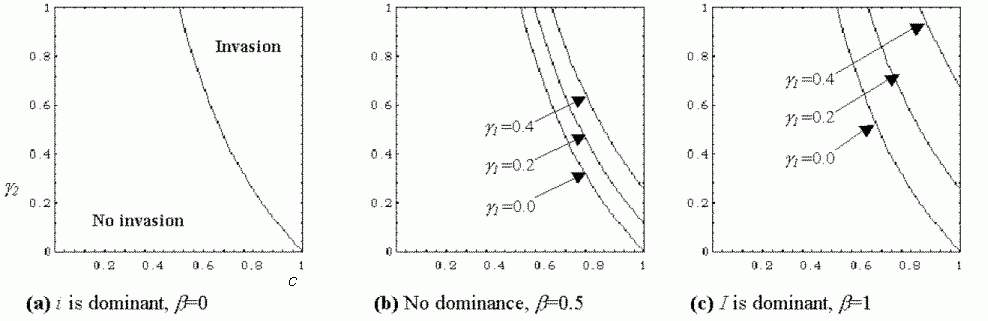
Figure 1: The conditions under which a population of B₀i individuals is susceptible to invasion from the I allele under different magnitudes of fitness cost, g₁ and levels of dominance (a-c), where g₂ is the fitness advantage of meme B₁, and c is the probability of social learning. Invasion occurs in populations with parameters to the right of the curved line.

The conditions under which a population of B₀i individuals is susceptible to invasion from the I allele under different magnitudes of fitness cost, g₁ and levels of dominance (a-c), where g₂ is the fitness advantage of meme B₁, and c is the probability of social learning. Invasion occurs in populations with parameters to the right of the curved line.

This result confirms Blackmore's intuition that there are conditions under which the selective imitation I allele can invade the population. These conditions are illustrated in Figure 1. It turns out that invasion is most likely when the fidelity of social learning, c and the fitness advantage of the B₁ meme, g₂ are high, whilst the dominance of I over i, b and the cost of selective imitation, g₁ are low. The conditions for invasion rely most heavily upon the reliability of social learning, c, that is, the fidelity of meme transmission, with no chance of invasion if c<0.5. However, it is possible that a high fidelity for meme transmission would already exist if we assume part 1 of Blackmore's hypothesis, that effective imitation has already evolved in the population. The result shows clearly that if bg₁ is high, there is less chance of invasion, as the inequality is less likely to be satisfied. If bg₁=1 the left hand side of inequality 2 reduces to 0, making it impossible for allele I to invade. Interestingly, I is less likely to invade if it is dominant over i.

It is possible for selective imitators to evolve if either b or g₁ is small, even if the other is large. That is, if there were little cost to selective imitation, it might evolve even if allele I is strongly dominant. Likewise, if allele i is strongly dominant, selective imitators could evolve even with a high cost. The effect of these scenarios is shown clearly in inequality 3. If we assume high transmission fidelity of the memes  and , then the condition for the evolution of selective imitators merely requires a fitness advantage to B₁ over B₀ (g₂>I ),

(3).

We have developed this example to illustrate how a hypothesis can be neatly formalized and tested under the phenogenotype paradigm. In our judgement the analysis suggests that there are realistic circumstances under which Blackmore's hypothesis may be operational. However, given that advantages of imitating appear to be dependent on the pattern of spatial and temporal variation in the environment, a more sophisticated analysis incorporating a changing environment might be an appropriate next step. Having illustrated a method for addressing the general feasibility of Blackmore's hypothesis, it is now open for further analysis.
 

4 Conclusions

Notes

1. If your browser has written 'g' instead of the Greek letter gamma, then you should note that ; ; and .

2.We consider the evolution of selective imitators, by assessing the local stability of the initial population consisting solely of B₀i individuals. Inequality (2) shows the conditions under which the B₀i population would be unstable, and susceptible to invasion from the I allele, and is calculated by finding the eigenvalues of the Jacobian matrix at . Invasion is restricted to parameter values that give the leading eigenvalue a magnitude greater than unity, indicating that B₀i is not asymptotically stable with a small perturbation from equilibrium.

References

[3] Boyd, R. & P. Richerson (1985). Culture and the evolutionary process, University of Chicago, Chicago.

[4] Boyd, R. & P. J. Richerson (1988). An evolutionary model of social learning: the effects of spatial and temporal variation. In Social learning: psychological and biological perspectives, ed. Zentall. T.R. & Galef Jr, G. B. pp. 29-48, Hillsdale NY: Erlbaum.

[5] Byrne R.W. & Whitten, A. (1988). Tactical deception in primates. Behavioural and brain sciences. 11(2):267-271.

[6] Cavalli-Sforza, L. L. F., M.W (1981). Cultural transmission and evolution: a quantitative approach., Princeton: Princeton University Press.

[7] Dennett, D. C. (1997). The evolution of evaluators. International School of Economic Research, Siena.

[8] Dunbar, R. I. M. (1993). Coevolution of neocortical size, group size and language in humans. Behavioural and brain sciences. 16:681-735.

[9] Feldman, M., K. Aoki & J. Kumm (1996). Individual versus social learning: Evolutionary analysis in a fluctuating environment. Anthropological Science. 104(3):209-232.

[10] Feldman, M. & L. Cavalli-Sforza (1976). Cultural and biological evolutionary processes, selection for a trait under complex transmission. Theoretical Population Biology. 9:238-259.

[11] Feldman, M. & L. Cavalli-Sforza (1979). Aspects of variance and covariance analysis with cultural inheritance. Population Biology. 15:276-307.

[12] Feldman, M. W. & K. N. Laland (1996). Gene-culture coevolutionary theory. TREE. 11:453-457.

[13] Holloway, R. L. (1981). Cultural systems and brain evolution. Dialectical Anthropology. 5:287-303.

[14] Humphrey, N. (1976). The social function of intellect. In Growing points in ethology, ed. Bateson. P.P.G., Hinde, R., pp. 303-317, Cambridge University Press.

[15] Laland, K. (1993). The mathematical modelling of human culture and its implications for psychology and the human sciences. British journal of psychology. 84:145-169.

[16] Laland, K. N., P. J. Richerson & R. Boyd (1996). Developing a theory of animal social learning. In Social learning in animals: the roots of culture, ed. Heyes, C.M. & Galef Jr., B.G. pp. 129-154, Academic Press, London.

[17] Lumsden C.J., Wilson., E.O. (1981). Genes, mind and culture: the coevolutionary process, Harvard University Press.

[18] Plotkin, H. (1994). Darwin Machines and the Nature of Knowledge, Penguin, London.

[19] Reader, S. M. & K.N. Laland (1999). Do animals have memes? Journal of Memetics - Evolutionary Models of Information Transmission, 3(2), http://cfpm.org/jom-emit/1999/vol3/reader_sm&laland_kn.html.

[20] Wilson, A. C. (1985). The molecular basis of evolution. Scientific American. 253(4):148-157.