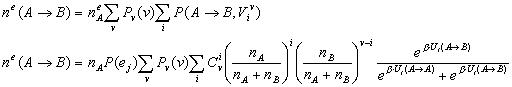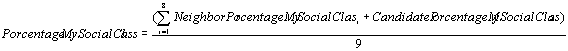The Design and Use of Integrated and Agent-Based Models for Freshwater Resource Management

Report of Workpackage 3 of the FIRMA project

1 Table of Contents

1 Table of Contents.. 2

2 Table of Figures.. 4

3 Summary.. 6

4 Introduction to WP3. 7

4.1 The use of software agents in simulation models. 7

5 An Overview of the FIRMA Models.. 12

6 Classifying the WP3 Models in terms of ABM benefits.. 20

6.1 Explanation of criteria and categories. 20

7 Scaling issues in water demand models. 24

7.1 Modelling Context 24

7.2 Model Design. 25

7.3 Conclusions. 34

8 Model of the pollutant diffusion according to farming practises : Phylou model.. 36

8.1 Modelling Context 36

8.2 Model Design. 37

8.3 Conclusions. 43

9 The Maaswerken negotiation model.. 45

9.1 Modelling Context 45

9.2 Original Purpose of Model 46

9.3 How was the Model Actually Used. 46

9.4 Relationship to other Models. 47

9.5 Model Design. 47

9.6 Static Structure. 54

9.7 Temporal Structure. 54

9.8 Important Parameters. 55

9.9 Initialisation. 55

9.10 Implementation Language. 55

9.11 Source Code. 55

9.12 Conclusions. 56

9.13 Methodological Lessons. 57

9.14 Future Development 57

9.15 References. 58

9.16 Published works relevant to the model 58

10 Metropolitan Area- Model for the Barcelona.. 59

10.1 Modelling Context 59

10.2 Model Design. 60

10.3 Conclusions. 73

10.4 Appendix I. Configuration of the simulation. 79

11 Multiple Models for Participatory Modelling in the Zurich Case Study 89

11.1 Domain context 89

11.2 Original Purpose of Model 89

11.3 How was the Model Actually Used. 90

11.4 Relationship to other Models. 90

11.5 Fulfilling FIRMA’s Objectives. 90

11.6 Model Design. 91

11.7 Conclusions. 98

11.8 Appendix A: Object model and interaction diagram.. 105

12 A model of water demand and social imitation.. 107

12.1 Modelling Context 107

12.2 Model Design. 108

12.3 Conclusions. 114

13 Bilateral versus multilateral negotiation.. 117

13.1 Modelling Context 117

13.2 Model Design. 118

13.3 Conclusions. 122

14 Neg-o-Net Version 1.0 model.. 126

14.1 Modelling Context 126

14.2 Model Design. 128

14.3 Conclusions. 134

14.4 Appendix 1. 137

14.5 Appendix 2. Neg-o-net Version 2. 138

15 The PANDORA Model.. 141

15.1 Relation of this model to the FIRMA aims. 141

15.2 Introduction. 141

15.3 Modelling Context 142

15.4 Model Design. 144

15.5 Conclusions. 146

15.6 APPENDIX.. 149

2 Table of Figures

Figure 1. An illustration of the relation of an agent-based simulation to its domain 7

Figure 2. An illustration of the relation of an equation-based simulation to its domain 8

Figure 3. The scope of the models over the levels 15

Figure 4. Relations between the model and the humans 26

Figure 5. UML description of the model 27

Figure 6. Dynamics in the model 33

Figure 7. Proportion of A behaviours for the households 34

Figure 8. Trends of A (sparing) proportion for households 35

Figure 9: Interactions among models and humans in the Phyle/Phylou process 39

Figure 10: UML class diagram of Phylou with main classes used in the model 40

Figure 11: panorama of relevant scales for basin study in Taurou valley 41

Figure 12: presence of pesticides on the plots in a depression landscape after 80 days (each red and blue point is featuring a fixed amount of two different molecules simulated) 43

Figure 13: simulations of amount of two kinds of pesticides at the outlet in a depression landscape (in pink are number of farmers supplying pesticides each day) 44

Figure 14. Negotiation scheme of Maaswerken agents 48

Figure 15. Finding a consensus strategy 49

Figure 16. Agent architecture 50

Figure 17. User Interface 51

Figure 18. Cross section 52

Figure 19. Example simulation output 56

Figure 20. General diagram of the model. 62

Figure 21. Text file to introduce temperatures of every month. 63

Figure 22. Diagram of a neighbourhood. 67

Figure 23. Diagram of the regions that are defined in a Municipality. 71

Figure 24. Number of citizens moving across municipalities. 74

Figure 25. Map of the municipalities. 75

Figure 26. Social classes distribution. 76

Figure 27. Distribution of water consumptions in the region. 76

Figure 28. Temporary evolution of the demand of water. 77

Figure 29. Temporary evolution of the demand of water for housing type in Barcelona. 77

Figure 30. People's temporary evolution. 78

Figure 31. Window of control of execution of the process. 79

Figure 32. ModelSwarm window. 80

Figure 33. ObserverSwarm window. 81

Figure 34. Window of the parameters of the families. 82

Figure 35. Configuration window of a Municipality. 85

Figure 36. Configuration window of Supply. 86

Figure 37. Configuration window of PolicyPrice. 88

Figure 38. Bargaining Algorithm- price negotiation 95

Figure 39. Decision Algorithm: Water Utility 96

Figure 40. The cumulative probabilities (CP) of values for three system indicators at the end of a 20 year simulation: the drinking water demand; the water utility profits and housing association profits (averaged over the final five years of the simulation). 99

Figure 41. Output Protocol from ZWG3 102

Figure 42. The Object Model of ZWG* 105

Figure 43. The Interaction Diagram of ZWG* 106

Figure 44. Structure of the model 109

Figure 45. The aggregate water demand resulting from a single run of the model 115

Figure 46. Distance between 2 agents in bilateral negotiation 123

Figure 47. Average distance between negotiating positions of agents in nine-agent simulation 124

Figure 48. Some illustrative viewpoints (simplified fragments) for three agents. Note that each node contains a label, indicator values and a list of possible actions. Arcs are labelled with (believed) required action(s) to make transition to new state 130

Figure 49. Example fragment of input text file to neg-o-net. 131

Figure 50. Example output from Neg-o-net model (I) 134

Figure 51. Example output from Neg-o-net model (Ii) 134

Figure 52. Example output from Neg-o-net model (Iii) 135

Figure 53. Example Neg-o-net output 137

Figure 54. Negonet version 1, negotiation structure 138

Figure 55. Negonet version 2, negotiation structure 139

Figure 56. Example output from negonet version 2 140

3 Summary

This report summarises most of the resulting models done in workpackage three of the FIRMA project. It does not cover all the models that were developed for the function of many of these were as prototypes, designed to inform the development of later models. The focus was the integration of the representation of social issues with the other issues in agent-based models and their participatory use with stakeholders. As was documented in workpackage two, it turned out that the problems and concerns presented by the five regions were very different. Instead of a ‘top-down’ approach to modelling, a ‘bottom-up approach has occurred – the modelling has been driven by the stakeholders’ concerns in the five regions rather than an academic concern for abstraction. However, core elements have emerged, especially in the areas of negotiation and participation and the integration of the different projects (workpackage 6) is already occurring.

The models that are described in this report demonstrate that agent-based modelling can be used to effectively integrate some of the different aspects of situations in a single model. They also show how an agent-based framework can facilitate a model’s participatory use and they show the huge potential that such models have in informing water management practices.

4 Introduction to WP3

Bruce Edmonds, Centre for Policy Modelling

4.1 The use of software agents in simulation models

One of the distinctive features of the FIRMA project is its use of software agents. In the context of water management, software agents are identifiable modules of code and information which separately represent actors[1]. Essentially what happens is that: each individual in the real world can be identified with a different module in the computational simulation; the behaviour of an individual is represented by the results of the corresponding module being executed in the simulation; and the interactions between actors are represented by the information passed between modules as a result of their execution together. This is illustrated in Figure 1 – the bi-directional arrows represent some sort of mapping or relation from the domain of study to the model, however these are not always either one-one or simple.

Figure 1. An illustration of the relation of an agent-based simulation to its domain

However these mappings are certainly more straight forward and transparent than those in more traditional analytic modelling techniques (Figure 2), where the equations tend to be representative of the whole domain in a more abstract way and the outcomes are only comparable via summaries (e.g. using statistical techniques).

Figure 2. An illustration of the relation of an equation-based simulation to its domain

This style of computer simulation has three big advantages:

1. It allows for a more descriptive or direct representation of the behaviour of actors, than is possible using mathematical or statistical models. The modules can be programmed so that the information traces resulting from their execution can be directly interpreted in a detailed way in terms of the actions and properties of the actors the modules are intended to represent.

Many traditional analytic techniques require the individual behaviour to be abstracted and summarised to a large extent before they can be formally represented in models. This abstraction/summarisation typically requires the use of very strong assumptions. Whilst agent-based modelling also involves some abstraction and the use of assumptions these are generally of a more plausible variety. Further, the finer-grained descriptive nature of most agent-based simulations facilitates the criticism of a model in terms of its abstractions and assumptions because the detailed behaviour can be interpreted in a more direct and intuitive fashion.

2. It enables the detailed behavioural traits of the actors to be related to the global outcomes. The behaviour of the actors is programmed into the modules which then interact when they are executed together and the collection of all the information traces produced can be summarised into what are considered to be the global outcomes of the simulation. These summaries can then be interpreted in terms of the global outcomes from the interactions of the actors they represent.

Most other modelling techniques essentially concentrate on either the micro-level (of individual behaviour) or the macro-level (of global outcomes). Agent-based modelling makes possible the conduction of computational experiments to see what global outcomes result from which individual behaviours, when this is analytically intractable (which it almost always is). One of the reasons this is important for the FIRMA project is because it allows for uncertain outcomes to result from the interactions within the models – the uncertainty is, to a limited extent, facilitated and captured internally. This contrasts with statistical models which, by their nature, involve the ‘averaging out’ of unpredictable tendencies in order to identify the ‘core’ trends. Thus agent-based simulations may reveal possible and qualitatively different outcomes that other model techniques may smooth away.

Similar techniques to agent-based modelling have been applied in many subject areas. The field of agent-based computational economics (ACE) has sprung up to examine how micro-economic models of behaviour (e.g. constrained optimisation) can result in macro-economic outcomes (e.g. equilibria) and the field of artificial-life has appeared to examine how life-like patterns and behaviour may be produced by the interaction of simple units. However, in these fields it is almost always the case that neither the micro nor the macro-levels in are straight-forwardly interpretable in terms of observations of the world, rather they are determined by a priori assumptions and concerns. Thus this style of model concentrates on advantage (2) above and, largely, ignores (1).

The above cases illustrate, in a negative way, the functional advantage of (1) in model formulation. A big problem with agent-based modelling is the fact that there are a great many ways of programming any particular simulation model – that is to say the model design is underconstrained by knowledge from the modelling context or problem domain. There are two responses to this problem: the first is to seek to constrain one’s model by prior tradition; and the second is to try and constrain it by making it descriptively accurate (or interpretable) in as many ways as is appropriate, but including at both the micro and macro levels. The first response epitomises the approaches of many groups and fields in North America, such as ACE and the Santa Fe institute. European social simulation, including the modelling in the FIRMA project has tended towards the second option. Of course, all modelling involves some prior constraint from tradition, in the form of known algorithms and programming styles etc., and all modelling involves some form of interpretation to something exterior to the simulation, but the difference in style and intent of the two schools is still marked, and potentially, important.

The relative descriptive clarity of agent-based models and the search for appropriate constraints upon simulation models has come together in the participatory uses of simulation models. The relatively straight-forward way in which agent-based models can be interpreted, makes their detailed and criticism by domain experts and stakeholders much more feasible. This allows for the knowledge of these people to be used to inform the content of the simulation models, in a way which is very difficult with more traditional analytic models. Ideally there is a tight developmental loop, where by a model is repeatedly presented, criticised, and re-designed until the participants are happy with both the design and outcomes. In this case the model ends up as an exemplar and focus of the participants’ understanding. It can be used to sharpen intuition about the way the processes can interact and, more importantly, can throw up new questions and issues to be examined. Thus the introduction of a simulation can affect the dialogue and decisions that may result – in this case, the model has an important role as a part of the social processes which contrasts with a traditional view of models representing a social process in a detached way. This important issue of participatory methods, including its relation to agent-based modelling is the subject of the forthcoming FIRMA work package 4. In this modelling work package the participatory aspects are relevant in two ways: in the use of the models, and as a means for their verification and validation (i.e. their constraints from the object domain).

The uncertainty of outcome, the underconstrained design, and the descriptive nature of agent-based models, means that they are more suited for identifying possible outcomes rather than predicting the most likely outcome. In this way this technique complements others such as statistical methods, which aims to predict the most likely outcome given a ‘surprise-free’ situation. How the possibilities are constrained and how the outcomes are interpreted in each model are thus core concerns.

3. The fact that agent-based modelling can be used to ‘unpack’ social processes and represent some of the component interactions and groupings (due to advantages (1) and (2) above), means that it is ideally suited as a means of integrating the modelling of these processes with models of other aspects (principally: climate, politics and business strategy). This is because the individual agents in the model can interact with the other aspects at suitable points in its simulated behaviour.

This fact is of great significance for the FIRMA project because the problems it is focussing on are of a complexly integrated nature. This means that the integration of these issues in our models is necessary if we are ever to capture and examine these domains. It is for this reason that a major aspect of the models in this report act to integrate the modelling or consideration of different aspects of a domain or situation, typically including the social and hydrological.

5 An Overview of the FIRMA Models

Bruce Edmonds; David Hales, Centre for Policy Modelling

In the original plan of work it was envisioned that we would design a “core model” which would be deployed in different versions for the five regional applications. However it quickly became clear that this was inappropriate. Rather than trying to ‘force’ the problems concerning those in the five regions into a single model (which would be bad science and even worse management), we seek to address the problems first and afterwards see what can be usefully abstracted. This change in emphasis can be seen as a direct result of the commitment of the FIRMA partners to the participation of the relevant stakeholders – faced with a choice of relevance to the problems and challenges presented by the stakeholders and adherence to an academic goal of abstraction, we chose the former.

A consequence of this is that no generic “core” model will be presented in this work package, rather there are a variety of models addressing the very different needs of each region. However, core elements and methodologies have emerged from this process. In particular a lineage of models on negotiation and a convergence of approaches integrating the participation of stakeholders with the modelling. A core negotiation model is being integrated with the “Zurich Water Game” as well as the Maastrict model concerning the Maaswerken political process.

In the following subsections will review the models with respect to the themes of: integration of different aspects using models; negotiation; the participatory input to and use of models; and water demand modelling. This section finishes with a general classification and comparison of the models in the form of a table.

5.1.1 Integration

All the FIRMA models either explicitly aim to capture aspects of social processes or are designed for use within a social process. Many of the models are designed to do both, and thus introduce an extra element of social reflection into the situation. These social aspects are integrated into all other aspects that are relevant to water management: hydrological, climatologically, political and economic. The models lie on a spectrum from purely participatory to purely representational. The models that could be characterised as including social process mostly by their use (i.e. at the participatory end) include: The Zurich Water Game; the Orb Water Consumption and Resource Evolution model and the Orb Pollutant Diffusion model. Those that to a great extent try to include the social processes within (i.e. the representational end) include: the Thames Household Water Demand model, the Bilateral Negotiation model, the PANDORA conceptual model and the Core Negotiation model. The remaining two models include substantial elements of both (i.e. lie somewhere in-between), being: the Barcelona Drinkable Water Management model, and the Maaswerken Negotiation model.

The models in this work package have shown, beyond doubt, that agents can be used to usefully integrate social processes with the other relevant aspects that impinge on the problem of water management. The stated aim of the FIRMA project was “to improve water resource planning through the use of multi-agent models that integrate physical, hydrological, cognitive, social and economic aspects of water resource management” – this work package represents a big step towards this goal with the provision of models which integrate these key aspects. This opens up the possibility of going beyond merely trying to influence society’s use of water but also to understand the interaction of the social process with the management, political, climate and business processes.

5.1.2 Negotiation

A theme that has strongly emerged during the course of the FIRMA project is that of negotiation. The inevitable conflicts of interest concerning the distribution, use and impact of water means that negotiation is inevitable and hence crucial to it successful management.

5.1.2.1 A Negotiation Framework

The concept of “negotiation” in everyday usage covers a wide range of phenomena and no single model could meaningfully capture all of these. However, all the models produced can be fitted into a general scheme, based on viewing negotiation as a collective cognitive process involving communication and planning.

Broadly (for the purposes of negotiation) agents (stakeholders) can be viewed as attempting to achieve some goals by planning sets of actions that they believe will help to bring about those goals. However, other agents may need to be persuaded to help in such plans. Such processes which involve communicative acts rather than direct force can be viewed as a negotiation process.

From this perspective agents can be said to have access to:

• Actions they can perform (Level 1)
• Beliefs about the world (Level 2)
• Goals they wish to achieve (Level 3)
• High level goals or “norms” (Level 4)

Negotiation processes may involve the communication and / or updating of each of these levels. Given this, models of negotiation may be categorised based on the levels involved and the methods by which communication and updating occurs on each level. For example, “auction” type models would involve Level 1 only, since one agent is offering a good or service in exchange for some utility or reward. No convergence of beliefs, goals or norms is required to affect an auction. Communication is restricted to offer bids and acceptance or rejection.

5.1.2.2 FIRMA Negotiation Models in Context

The majority of the negotiation models within FIRMA concentrate on Level 1. Not because they are based on an auction protocol but because the underlying beliefs of the agents are either hard-coded into algorithms (Zurich model) or they are not explicitly represented at all (Maastricht model)[2]. The Manchester generic model (Negonet) has explicit and dynamic representations of goals and beliefs and currently operates on both Levels 1 and 2 – communicating and changing beliefs under certain circumstances, as well as “action haggling” (see relevant Negonet section in this report). Error! Reference source not found. shows the levels at which the different models focus. Notice that Negonet can in theory subsume the three other models, but is distinct and complementary to PANDORA. On-going work between CPM and ICIS is being carried out to attempt to integrate Negonet with the Maaswerken model. This requires additional information from stakeholders concerning their beliefs and when they change. This indicates a further empirical study of stakeholder behaviour under simulated negotiation processes. A long term aim may be the integration of PANDORA with Negonet – however, PANDORA is yet to be implemented – though a detailed design is resented in the relevant section of this report.

Figure 3. The scope of the models over the levels

5.1.2.3 Negotiation Model Specifics

As in other areas of FIRMA, the development of the models has progressed in two directions: in the representation of negotiation processes in models and the use of models to aid negotiations.

In the former category are: the multilateral negotiation model, Negonet and PANDORA. The first of these investigates the source of difficulty apparent in negotiations involving more than two parties. The negotiation is here represented as multi-dimensional haggling. The content of the dialogue is to agree a set of values (chosen from a small set) when each participant has different goal values and ascribes different importance’s to each. The content of the negotiation is a sequence of offers and, possibly acceptances, which may or may not converge to an agreement.

The Negonet model does not deal with the issue of coalitions, but with simulating a richer negotiation dialogue that results when parties with different views as to what is possible in the real world try to reach their separate goals. Thus this adds the fact that different parties have qualitatively different views of the world as well as different goals and adds requests for offers and denial of possibility into the simulated dialogue. This model is informed by the work of ICIS which is looking at the Maaskerken negotiation process concerning flood defences in the Limburg basin and the second version of this model will be an application of the core model to simulating that process.

The PANDORA conceptual model seeks to go beyond the interchange of offers to include the interchange and adoption of goals. It thus seeks to map out the future direction that models of negotiation may take.

In the more participatory category of negotiation model are: The Barcelona Drinkable Water Demand model; the Maaswerken Negotiation model; the Zurich Water Game; the Orb Consumption and Resource Evolution model; and the Orb Pollutant Diffusion model. All of these models are designed to be used as a part of a participatory process involving negotiation. The first two include aspects of possible interactions and negotiations processes among the stakeholders in the models, whilst the two Orb models are designed to be representations of the dynamics of the system that can be used in public consultation and allows to explore the potential consequences of different options.

5.1.3 Participatory Input and Uses

With the exception of the two abstract models all the FIRMA models include participatory aspects. This will be covered in a large part by work package 4. However, the development of the modelling and of the participation can not be completely separated – the two aspects have co-evolved to a considerable extent. All the non-abstract models have been designed to ensure that they will be or are suitable to a participatory use – this is important since it has become clear that participatory use cannot simple be “bolted-on” as an after-thought, but needs to be a fundamental concern in model design from the earliest stages. The participatory input is also a valuable way to inform model design, an aspect greatly facilitated by the descriptive agent-based nature of the models.

The models can be divided into those that use participation primarily as an input to the model design and those which are designed for use in a participatory process. The Thames Domestic Water Demand model, Barcelona Drinkable Water Management model, and the Core Negotiation model are designed to take into account (or in the later case take input from) relevant stakeholders. The Limburg Maaswerken Negotiation model, the Orb Consumption and Resource Evolution model and the Orb Pollutant Diffusion model are designed so that the outcomes of the model are comprehensible to stakeholders so that they may interpret the results, and understand the underlying model processes. The Zurich models were designed with significant input from the participatory process. They were supposed to reflect the mental models and perceptions the stakeholders use in their reasoning in order to support processes of social learning.

5.1.4 Water Demand

The growth in general affluence and in urban populations means that there is likely to be an increasingly sharp competition for the use of common water resources. It is possible that climate change will make this problem worse. Part of the solution to this is the better prediction of demand and better management of the water supply. This implies the better understanding of how social processes could change the demand for water. However, increased understanding is not enough, there is likely to be an increased need for political settlements between the different interests.

Four of the FIRMA models address the problem of water demand management. The Thames Household Water Demand model and the Barcelona Drinkable Water Management model are designed to investigate the impact of social process on the domestic demand for water. In the former case the social process is one of imitation and uptake of patterns of use of water consuming devices and the later focuses on the impact of household location and reallocation on the demand. In contrast the Zurich Water game and the Orb Consumption and Resource Evolution model are designed to be used to facilitate public discourses concerning the balance of interest between stakeholders in terms of water distribution and use. In most of the models the problem is the difficulty in meeting demand for water, in the Zurich case the focus problem was one of over-supply.

5.1.5 Management of Water Crises

Man’s increased impact upon the environment and likely climate change have increased the likelihood of some natural crises, including: flooding, water shortage, and the spread of pollution. All of these problems involve the interaction of different processes: social, business, political, land use and climatologically, and their better understanding requires that the interaction of these processes be modelled. As with water demand, the solution to these cannot be simply as a result of better understanding but also requires political decisions as to the way forward.

Three of the FIRMA models touch on the problem of water shortages: Thames Household Water Demand model, the Barcelona Drinkable Water Management model and the Orb Consumption and Resource Evolution model. The focus of the Thames model is the reaction of interacting clusters of households during periods of drought. In recent years the publics reaction to exhortation to use less water in times of shortage has changed and this model is one attempt to examine this issue. The Maaswerken negotiation model is of the attempt to reach consensus over flood protection and amelioration measures. The next version of the Core Negotiation model will be to directly simulate this process, so it can be integrated into the Maaswerken model.

5.1.6 Summary of FIRMA models

For ease of reference a table summarising these overlapping aspects of the 9 presented models is shown in Error! Reference source not found..

This work package does not describe all the models that were developed as a result of the FIRMA project, for many of the models (e.g. Rome’s Part-net model, Koblenz’s lake Anderson model, their model of drought management for a role play at Oxford and their model of basin flow, and the CPM’s earlier models of negotiation) role was to inform the development of later models described herein. A complete historical deconstruction of the influences of one model upon another would be time-consuming and contentious – when partners work together as closely as those of the FIRMA project it is inevitable that there will be a dense web of influence. This is one of the main purposes of such joint projects, that the results may be more than merely the sum of the parts, but it does also mean that disentangling the different views of academic precedence is neither possible or helpful.

Table 1. A comparison of FIRMA models

6 Classifying the WP3 Models in terms of ABM benefits

Matt Hare, EAWAG, Zurich

6.1 Explanation of criteria and categories

The criteria in Table 2, upon which the models are classified, are based upon six perceived benefits of using an agent-based modelling methodology, i.e. the ability to couple social and environmental models and to model micro-level decision making, social interaction, intrinsic adaptation of decision making, population level adaptation and multiple scale level decision-making, and how the design of the models make use of such benefits. These criteria are taken from Hare & Deadman (submitted) which is a very much improved version of a presentation given at MODSIM 2001, in Canberra, Australia (Hare et al. 2001). I have taken only the applied management models in WP3 since the criteria do not apply to other types of model (e.g. nego-net, which will later become a part of the Maaswerken model).

6.1.1 Criterion 1: enviro-coupling.

The categories here represent whether or not the link between the social model and the physical environmental model (e.g. rainfall, flooding) is explicit or non-explicit.

non-explicit - the physical environment is modelled as a series of equations that do not link to a specific location within the space that the agents occupy. For example in the Barcelona and Thames models, although space is explicitly represented in terms of a grid of neighbours, the environment, represented by rainfall, is linked to the entire space via a PET model (in the case of Thames), rather than to specific locations within that grid of agents.

explicit - environmental space is represented explicitly (e.g. by a raster grid) AND environmental factors are linked to specific areas of that space. In the Maaswerken model, for example, inundation is calculated for each specific cell of the land about which the agents negotiate.

Criterion 2: decision making.

This refers to the method in which an agent, in isolation, decides on its behaviour at any one point in time. Social interaction and adaptation are considered in later criteria. Decision making can occur through the use of rules to control behaviour, equations or objective functions etc.

6.1.2 Criterion 3: social interaction.

This represents how the agents interact socially and for what purpose.

Social interaction can occur for the purposes of social adaptation as well as to carry out group tasks.

Social adaptation - agents adapt their behaviour by imitating or learning from the behaviour of their peers. Social adaptation is usually modelled using many agents who interact simply and locally with neighbours, e.g. in the Thames and Barcelona models.

Group tasks - agents will interact for purposes of negotiation or group decision making. Group task activities, are usually modelled using few agents, e.g. in the Maaswerken and Zürich models, whose decision making may sometimes be more cognitively complex.

6.1.3 Criterion 4. Intrinsic adaptation.

This represents how the agent adapts its decision making behaviour out of its own volition in response to feedback from the environment, rather than as a result of social interaction. This can occur through fine tuning as well as multiple strategy adaptation.

Fine tuning - parameters in a set of rules or equations are altered in response to perceived errors between expectations and reality.

Multiple strategies - the agent has a variety of decision making methods at their disposal (imitation, repetition, and deliberation) and switches between them depending upon the level of success or some other criterion. In the Thames model endorsement values are attached to particular rules which control whether or not the agent imitates, deliberates, or obeys authority. The endorsements function as a conflict resolution device. The rule with the currently highest endorsement is used.

6.1.4 Criterion 5: population adaptation.

This represents whether or not selective pressure is applied to the population of agents so that the aggregate behaviour of the population as a whole adapts over time. Selective pressure, as in evolutionary theory, results in the removal of agents that fail to meet particular criteria. In the Barcelona model, family member on reaching a certain age have a chance of dying. When a family has no more members, it disappears from the housing.

6.1.5 Criterion 6: Multiple-scale decision making.

This represents whether there are decision making agents in the same model which make decisions at different scale levels, e.g. in the Thames model there are individual householders making decisions for their family and policy agents making decisions for the entire city - this is an example of the use of multiple-scale agency. The use of multiple-scale rules on the other hand occurs when the same agent can make use of decision making rules (or equations) to guide their behaviour at more than one scale level. For example, a householder may have rules to determine its own individual water demand as well as rules to determine how it makes community scale level decisions with other agents about water usage.

6.1.6 References

- Hare, M.P. & P. Deadman, (submitted). Further towards a taxonomy of agent-based simulation models in environmental management., Submitted to Mathematics and Computers in Simulation.

- Hare, M.P., P. Deadman, and K. Lim. (2001). Towards a taxonomy of agent-based simulation models in environmental management., p. 1115-1122, In F. Ghassemi, et al., eds. Integrating models for natural resources management across disciplines, issues and scales. MODSIM 2001. 10-13 December., Vol. 3: Socioeconomic systems. MSSANZ, Canberra, Australia.

Table 2. Some of the management models in WP3 classified in terms of how their design make use of 6 benefits of agent-based modelling.

7 Scaling issues in water demand models.

Margaret Edwards, François Goreaud, Sylvie Huet, Guillaume Deffuant, LISC, Cemagref

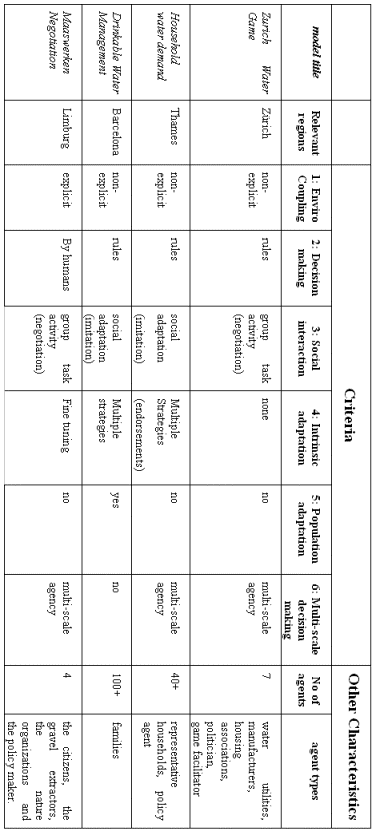
Models connecting water consumption and resource evolution at different levels of aggregation (example of the Orb valley)

7.1 Modelling Context

7.1.1 Description Domain Context

This model deals with water quantity in the Orb River Basin (which impacts on water quality). Water withdrawals depend, on the one hand, on agricultural practices linked to irrigation, on the other hand, on domestic use, which vary in time and over the year.

It will be an element in the reflection upon linking models of water and population at different scales; and more specifically, the possible advantages in this context, of individual over aggregate description for the population sub-model. In the series of models we will implement, we consider hydrological models defined at two grains (different size of sub-basins), and population models, which are individual-based and aggregated in spatial cells.

Our modelling choices, influenced partly by constraints in terms of time of development (and acceptable complexity of the sub-models relative to the study of their linking), has led us to focus on the question of resource quantity. This question is directly important mainly for irrigation (and impact in a minor way on tourism by enabling or preventing certain activities, such as kayak), and indirectly on tourism, by worsening eventual quality problems (by increasing concentration of pollutants).

A links is performed over aggregate withdrawals, on the one hand and feed-back of the state of the resource on the other hand. Water consumptions evolve depending on the social context and on the state of environment, and impact on the water resource.

The link will not be made at the same level depending on the scale of the submodels; individual-based description on the population allows a diversified feedback of the environmental state on the population; finer hydrological description of the basin, may bring to light a crisis situation which does not appear at an aggregate level (where a positive balance is respected).

7.1.2 Original Purpose of Model

The purpose of the model is to link water and population dynamics, by a double link: the impact of human behaviour (water consumption) on the resource, and the impact of the evolution (or the state) of the resource on the evolution of the population (choice of consumption).

In the participatory process, its purpose is to describe the interrelations of processes in a realistic way, as a support for discussions and for the evaluation of various scenarios around water management in the basin. It will also be an element of comparison with other models at different scales (see Context).

7.1.3 How was the Model Actually Used

It is still currently in progress.

7.1.4 Relationship to other Models

In the series of models we will implement, we consider hydrological models defined at two grains (different size of sub-basins), and population models, which are individual-based and aggregated in spatial cells. Therefore, we consider here a series of models rather than a single one. These models are defined at different levels of aggregation, but they share as much as possible the same assumption in order to make relevant comparisons.

The design of the links between the individual based and the aggregated model of population is made by considering probability densities of agents in different states and the probability of flow of density between the states (socio-dynamic approach).

7.2 Model Design

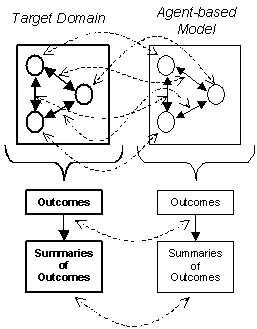
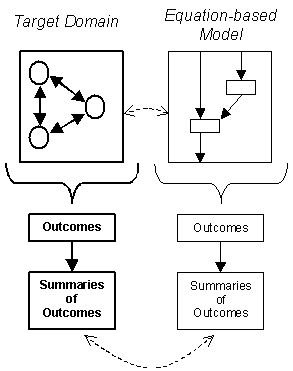
7.2.1 Intended interpretation

This model takes sense in a series of models. The purpose is not to be predictive, but to compare population and water models linked around the question of quantitative evolution of the resource, at different scales; this is from a theoretical point of view, in terms of behaviour of the model and precision; but also from a participatory point of view (not totally disconnected) in terms of how expressive it is to the stakeholders (objects and processes) and of the playability of the model.

7.2.2 Original Sources for Model Design

· global modelling of hydrological processes (GR2m model) will be used at different levels of spatial aggregation. We use this model to simulate the evolution of the resource according to the rainfall data. This model was developed by Cemagref and calibrated on several sub-basins of the Orb valley

· individual level model is used for the population based on the model general threshold model of innovation diffusion (described by Peyton Young, Valente, Grannoveter… among others). This model was developed by quantitative sociologists, and happens to be easily formalised in game theory and automata networks.

· an aggregated population model based on socio-dynamics will be used next, it will be based on the sociodynamics theory (Elbing, Weidlich, Haag), which uses techniques from physics (derivation of a master equation).

7.2.3 Relations between the model and the humans

The next figure describes the relations between the models and its potential users.

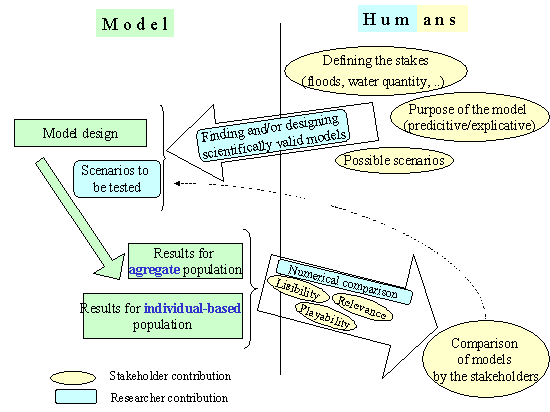
Figure 4. Relations between the model and the humans

7.2.4 Static Structure

The static structure of the model is synthesized in the Figure 5. Main items are the population, the river sub basin (flow, resource); the link takes place through the withdrawals and environmental indicator(s).

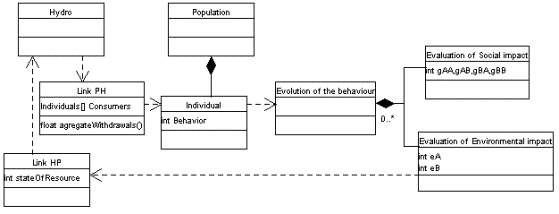
Figure 5. UML description of the model

7.2.5 Temporal Structure

The dynamics follow several time steps:

· month for the evolution of water resource, which depends on previous state, rainfalls and withdrawals

· finer temporal scale for the social interactions and consumption behaviours ; we model the diversity in water consumption behaviour by letting the withdrawals vary around a mean ; the variation (under or over the mean corresponding to respectively A or B behaviour) is the object of decision of the individuals. This choice is to depend partly on an individual’s social context, and on the state of the water resource, to which each individual can be more or less sensitive: the individuals randomly chosen to evolve, question their relationships on their opinion, and depending on their own present one, evaluate the social and environmental gain to maintain their kind of consumption or to change it. Social gain is determined by the relative proportions of relationships following one or the other of the behaviours, weighted by parameters of the model. Environmental interest in changing consumption is only taken into account if the environmental indicator attains a given threshold, which may vary in the population. (This indicator is actually represented by the mean flow over the month). The weight of the state of the environment in the decision is proportional to the overdraw of the indicator. The probability of choosing A is described in the paragraph "Key Algorithms".

· For each month, a new state of the water resource is computed. The dynamics and interaction between the several features are voluntarily simple in order to facilitate comparison between the different levels of representation for water and population dynamics.

7.2.6 Important Parameters

(a) number of links in the social network,

(b) frequency of interaction (in relation to the hydrological time step),

(c) sensitivity of individuals to social influence versus conscience of environmental state

(d) threshold of significance for the environmental indicator

7.2.7 Initialisation

· Parameter fitting is used for the hydrological model, through rainfall, ETP data.

· Global statistical indicators allow us to simulate a fictive population. More precisely, the following features are known or estimated following the Orb case :

- Total number of households and of farmers

- Mean monthly consumption for a household, mean monthly water use per hectare for irrigation, total surface of irrigated land

Parameters directly provided by the user.

GENERAL PARAMETERS
	Parameter	Type	Remarks	Reference Value
P1	Number of simulations	int		100
P2	Error admitted for the results	float	(0<..<1)	0.05
P3	Name of the river-basin	String		Orb
P4	Number of sub-basins	int	1	1
P5	Number of time-steps	Int	(12 * years)	120
P6	Proportion of individuals evolving at each time step	float		0.1
P7	Kind of evolution	int	0 : determinist 1 : probabilist	1
P8	(exponential parameter in the probabilistic case)	float	(otherwise ignored)	1
FOR EACH SUB-BASIN
P9	Name of the sub-basin	String
P10	Surface	float		1330
P11	hydro parameter 1	float		400
P12	hydro parameter 2	float		394.7513
P13	hydro parameter 3	float		100
P14	hydro parameter 4	Int		0
P15	hydro parameter 5	Int		1
P16	hydro parameter 6	String	File with rainfalls and ETP	PETPTabarka90.txt
P17	Constant monthly withdrawal	Float		0
P18a	Number of Farmers simulated/true number of farmers	float		1
P18b	Number of Households simulated/true number of households	float		7.8
P19a	Kind of population simulated	Int	0 : individual-based 1 : aggregate
P19b	Number of individuals to simulate	Int		10000
P20	Proportion of A behaviours (sparing) simulated	float		0.44
P21	Proportion of farmers in the simulated population	float		0.004
P22	Mean number of farmer relationships for a farmer	Int		7
P23	Mean number of household relationships for a households	Int		7
P24	Number of relationships between households and farmers	int
P25	gAA for the farmers	float	Parameters of social influence	0
P26	gAB for the farmers	float		1
P27	gBA for the farmers	float		0
P28	gBB for the farmers	float		1
P29	Weight in the decision of the environment (farmers)	float	Parameters of environmental influence on the decision	1
P30	Threshold of state of resource (farmers)	float		4
P31	gAA for households	float		0
P32	gAB for households	float		1
P33	gBA for households	float		0
P34	gBB for households	float		1
P35	Weight in the decision of the environment (households)	float		1
P36	Threshold of state of resource (households)	float		4

Besides : two files

‘ConsoAgri’ and

‘ConsoCit’

in the main directory, provide the monthly mean water consumption for farmers and households (in m³).

The factors of multiplication of the basic demand corresponding to the A and B behaviours are for the moment still directly defined in the classes Farmer (‘Fermier.java’) and Household (‘Citadin.java’). We suppose that the multiplication factors of mean water use, for the two behaviours are respectively 0.8 and 1.2 for the households, and 0.1 (corresponding to very basic needs) and 1 (in case of irrigation) for the farmers ; these numbers do not have a statistical basis, but their purpose is to allow a first survey of the inter-dependence of the dynamic features of the model.

The distribution around the mean number of relationships is defined in the class generating the group of simulated individuals (‘PopulationIndividuCentree’ (= IndividualBasedPopulation)).

7.2.8 Key Algorithms

· Change in consumption behaviour following social interactions (adapted from a model studied by Peyton Young).

Individual-based model

We consider a population of individuals characterized by their behaviour (A or B). A represents a sparing use of water, B a non-sparing use of water.

The utility to go to behaviour A from a behaviour X (A or B) is expressed as

Where the g_XY are parameters of the model,

n_v^A is the proportion of social relations/friends who have an A behaviour

e_A is an environmental utility which depends on the state of water resource and varies in time ; its value varies in the following way :

for levelOfResource > criticalThreshold,

e_A =0

for levelOfResource £ criticalThreshold,

e_A = a (criticalThreshold- levelOfResource)

Conversely the utility of adopting B is expressed in a similar way by replacing the A index by a B index in the previous formula.

The probability for an individual of adopting A is then expressed as a function of the utilities:

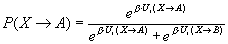
Aggregate-level model for the population

let n_A be the number of individuals of A behaviour in the considered population

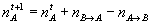
we suppose that :

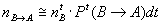
from which :

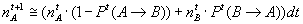
By considering the probability of change of behaviour in the population, from the individual-based model, we obtain for the aggregate level :

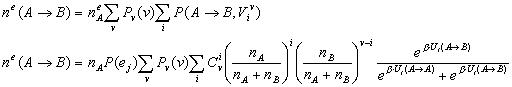
Where V_i^v corresponds to v relationships out of which I follow an A behaviour.)

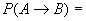
Supposing this population has LE links towards another population with nA' individuals of A behaviour, and nB' , of B, the probability of change from A to B becomes :

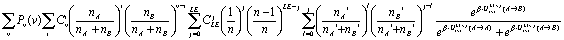
· Rainfall - Outlet Flow (parameter fitted model) for the water resource.

7.2.9 Description of Model Dynamics

Consumption evolves following discussions between the individuals, and the level of water, thereby impacting on the resource. The resource itself depends on the rainfall data and withdrawal

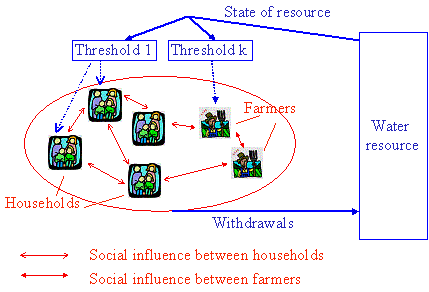
Figure 6. Dynamics in the model

7.2.10 Implementation details necessary to get the simulation to run but not considered important for the results

- The simulations are launched from the class MultiSimParam, for a few set of parameters (one per line of the file), with the name of the parameter file, and the numbers of the first and the last line of parameters to be specified when called. In this case, the first element of each line of parameters is the name of the directory which stores the results. The directories are automatically generated.

7.2.11 Implementation Language

Java

7.2.12 Source Code

Information can be obtained from the research team

7.3 Conclusions

7.3.1 Example Simulation Output

7.3.2 A mean over various simulations is computed, as well as the bounds of a confidence interval for an error of 5%, to allow a more significant comparison between sets of parameters. Figure 7 is an example for the evolution of the sparing (A) behaviour for the households, for a low dependence to state of resource.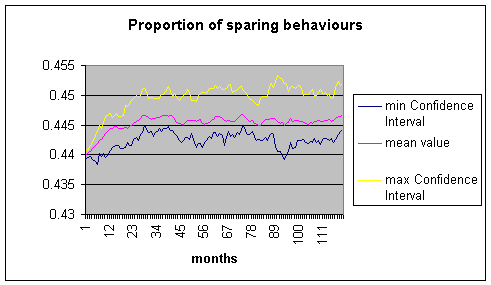

Figure 7. Proportion of A behaviours for the households

In Figure 8. we see two different trends for different weight of state of resource in the decision of choice of behaviour.

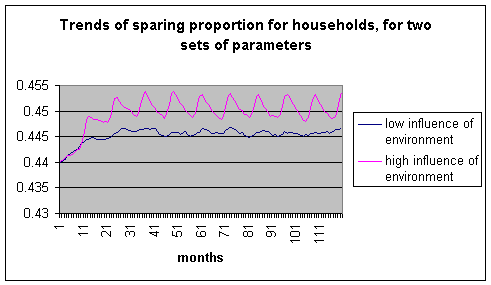
Figure 8. Trends of A (sparing) proportion for households

7.3.3 Methodological Lessons

The stakeholders expressed their need for models which throw light on interactions and interdependence of processes (in the river-basin), of different kinds and/or spatially distributed. The way in which the results provided by the model are presented is also important. Synthesised results and an eloquent interface (taking up reference elements of representation for the stakeholders) are to be favoured. (For example, realistic or symbolic maps are preferable to abstract representations of space (such as a geometric form).

7.3.4 Future Development

Complete different links between models of water and population in order to determine the possible advantage of individual-based over aggregate description of the population sub-model.

7.3.5 Published works relevant to the model

Edwards, M.; Goreaud, F.; Barreteau, O.; Cernesson, F.; Hill, D. - 2002. An object-oriented model linking hydrological and social processes at an aggregate level. Présentation orale et article dans les actes du 'Workshop Agent-Based simulation 3, special session on Simulation and Environment ' (SCS), à Passau (Allemagne), 7-9 avril 2002, 6 pp.

8 Model of the pollutant diffusion according to farming practises : Phylou model

Olivier Barreteau, UR IRMO, Cemagref

Anne-Laure Borderelle; Flavie Cernesson, UMR 3S Cemagref/ENGREF

8.1 Modelling Context

8.1.1 Description Domain Context

The model aims at representing the wine growing practices and their consequences on the diffuse pollution in a Sub-basin of Orb River. This takes place in a double frame:

· River Contract of Orb Valley which aims at facilitating concerted and balanced water management at basin scale and promotes co-ordinated action among its members, it is managed by a basin institution “Syndicat Mixte de la Vallée de l’Orb” (SMVO),

· an on-going diagnosis of non-point source pollutions caused by pesticides on a sub-basin of Orb river, the Taurou, managed by SMVO with Chamber of Agriculture. This study aims at starting negotiations on actions to enforce to limit such pollution because of drinking water pumping at downstream of this sub-basin.

Following works with SMVO at the basin scale on collective water management, identification of stakes and potential use of agent based models to facilitate dialogue, we chose this field as an application. We focus then on the relations between heterogeneous localised practices for herbicide and pesticide management and presence of undesired molecules in drinking water resource which is taken at the downstream of this sub-basin. This sub-basin is mainly used for wine-growing activity, which involves according to their production patterns different kinds of pesticide uses by winegrowers.

8.1.2 Original Purpose of Model

The original purpose of the model is to study the possibility of using an Agent-Based Model to facilitate the discussion within such an on-going negotiation process. The model is supposed to be helpful in the discussion about scenarios of action: for the elaboration of possible scenarios, and the discussion about the decision to adopt one or the other.

From a methodological viewpoint, we have chosen to built the model through a dialogue with key stakeholders. Such “co-building” has got three main goals:

· reaching models which are not too far from local stakeholders languages in terms of environmental and socio-economic indicators as well as in terms of scales,

· specify features of interface to prevent misuses,

· increasing the probability of use of the model.

8.1.3 How was the Model Actually Used

The implementation is currently in progress by nature of the design process. Three versions of this model has already been implemented. They have been used in two different settings:

· in scheduled meetings with the key stakeholders involved in the participatory model design for the three of them: they have commented each version, proposed modifications and asked for specific features;

· with institutions involved in the diagnosis study for the first version so that they might understand what kind of models it is a matter of, as well as they might comment main assumptions.

8.1.4 Relationship to other Models

There is only a weak link with a few physical model for transfer and decay of pesticides molecules according to plot borders nature (ditch, hedge…) and topographical characteristics (slope, direction of vine rows according to slope). Algorithms used to specify chemicals behavioural patterns are derived from “classic” physical models and validated through a comparison with them.

8.2 Model Design

8.2.1 Intended interpretation

This model is intended to make people discuss on collective use of pesticides and their impacts on drinking water quality downstream. This means that it should have corresponding elements which entails stakeholders to discuss about their real basin on the basis of simulations on the virtual basin which constitutes the model. However this correspondence must not be to precise at the finer grain in order discussions go towards shared processes and eventually common rules instead of individual consequences. Therefore we’ve gone towards an archetypal basin with correspondence elements dealing with:

· diffusion process of chemicals,

· overall layout of basin,

· classification of chemical use practices.

8.2.2 Original Sources for Model Design

Physical patterns of the model are based on simplification of existing models from literature validated through interviews of experts. This deals notably with transfer of pesticides and distributed modelling of hydrological processes.

Space representations are based on original field work for description of the four various kinds of landscapes in Taurou sub-basin. Three places have been randomly chosen and analysed in each kind of landscape for five items:

· size of plots,

· soil use (and notably rate of plots with grass or forest instead of vine),

· width of inter-plot borders,

· kind of inter-plot borders among five categories: track, ploughed, grass, hedge, ditch,

· kind of practice for weed management (on rows or in-between rows).

This entails to describe typical space composition of each kind of landscape.

Thus practices are based on Chamber of Agriculture reports as well as on these field observations. They are described according to the place pesticides are put in plots and the amount of pesticides which is put according to rates recommended by pesticides sellers:

· on rows or in-between rows,

· organic, conventional (full use) or limited use (one third of recommended amount).

They have been validated through interviews of a sample of farmers in the sub-basin.

Relations between models and humans

One of main features of this experiment is the choice of a co-design of the model with some key stakeholders, who are potential users of that kind of tools. More than advertising for this kind of model, it is more a question of increasing their awareness on what can be done and not done with these models. This is a way to tackle validation issue: valid use domain of these models is supposed to be better grasped by stakeholders who have participated in their design.

There have been three main steps which are summed up in following Figure 9.

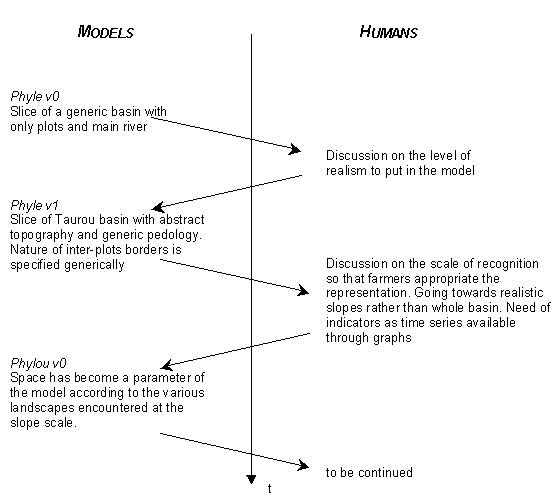
Figure 9: Interactions among models and humans in the Phyle/Phylou process

8.2.3 Static Structure

In the current state, Phylou0 is mostly dealing with reactive entities. They are described by UML class diagram in Figure 10.

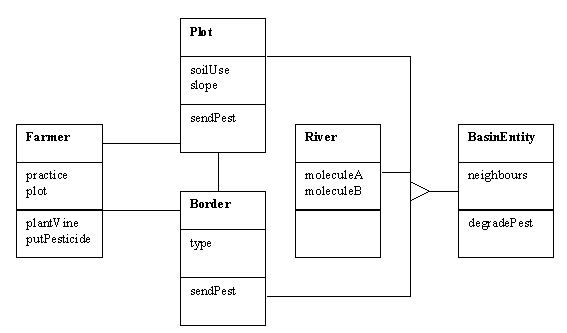
Figure 10: UML class diagram of Phylou with main classes used in the model

This diagram presents the additions of Phylou on top of Cormas platform. Each space entity inherits from AggregatedSpaceEntity class of Cormas. Space representation in Cormas is composed of cells as a Cellular Automaton (Bousquet et al., 1998).

8.2.4 Temporal Structure

Three main time steps are considered:

- cropping season corresponds to the whole simulation length, landscape and plantations are considered fixed at this time scale,

- day is time step for action of farmers, to choose to put chemicals or not.

- smallest time step is 6 seconds for the dynamics of chemicals and water from one cell to another.

In any case, each farmer who puts pesticide on his plot makes two supplies to his plot, on short time stages given for all farmers. Farmers who puts a little pesticide choose time of bringing according to the rain while not farmers with full supply.

Rain is given according to a real time series of rain in the area (rains of 1995). It is the engine of transfer but is considered as external and fixed for all simulations.

8.2.5 Important Parameters

In current version, two main categories of parameters are key to understand the overall behaviour if the system. They are those on which we make the sensitivity analysis.

First farmers’ practices are determining the overall amount of pesticide supplied in slopes. This determines the input in the system which then might be transferred to the river or degraded in plots or borders.

Second, space pattern is allowing or blocking the access of pesticides to the river. Rates and space organisation of various soils occupation for plots and borders (respecting the observed proportions for plots) and of types of farmers constitutes different space patterns which are simulated.

Choice of whole space scale has been one of main results of the interaction process with stakeholders. Figure 11 presents the various space scale which are relevant to a basin approach.

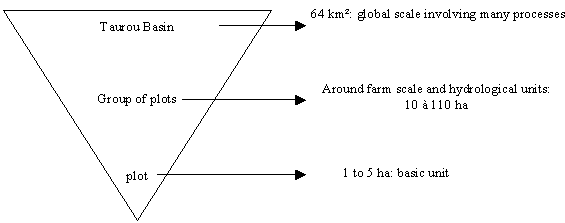
Figure 11: panorama of relevant scales for basin study in Taurou valley

Meetings with stakeholders have lead to choose group of plots or slope as the main space scale, to be recognised by farmers and on which test scenarios of space patterns. Finer grain has to stay archetypal. Larger grain, whole basin, is beyond scope of the model in its current version and is going to be either on manager’s role or in a new version a composition of current scale, not necessarily with same architecture.

8.2.6 Initialisation

Initialisation deals mainly with the constitution of the landscape pattern to simulate and loading of rain file.

8.2.7 Key Algorithms

Pesticides are described with their rate of decay and solubility. Main process is following a rain event the transfer of remaining pesticides in plots to the ditches network and then the river. Table 1 explains the transfer according to various possible soil use.

Table 3: transfer rates according to soil use

8.2.8 Description of Model Dynamics

After each rain event provided by rain file on a daily basis, the “6 seconds” time steps is activated until all water has been drained to the ditch network or the river. It simulates this draining of the rain on the landscape taking along some of the pesticides located on plots at the moment of drainage.

Otherwise the time step is the day for rain file activation as well as for choice of pesticide supply by farmers, during the time slots fixed in the model.

8.2.9 Implementation details necessary to get the simulation to run but not considered important for the results

Landscapes patterns are stored in map files. They are created apart from the simulation in a raster format.

8.2.10 Implementation Language

We used SmallTalk on top of Cormas platform

8.2.11 Source Code

Information may be obtained from the research team as code files. Cormas and VisualWorks’ SmallTalk are required to run it. They can be downloaded from Cormas website: http://cormas.cirad.fr

8.3 Conclusions

8.3.1 Example Simulation Output

First output of simulation is the evolution of presence of pesticides in plots with time. They disappear progressively with time and move towards downstream after rain events. Figure 12 is featuring this part of interface for depression landscape.

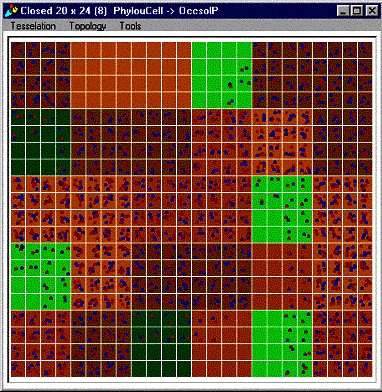
Figure 12: presence of pesticides on the plots in a depression landscape after 80 days (each red and blue point is featuring a fixed amount of two different molecules simulated)

Simulations are providing time series of presence of pesticides at downstream point of each landscape simulated. Figure 13 is presenting such output for various rates of ditches among borders.

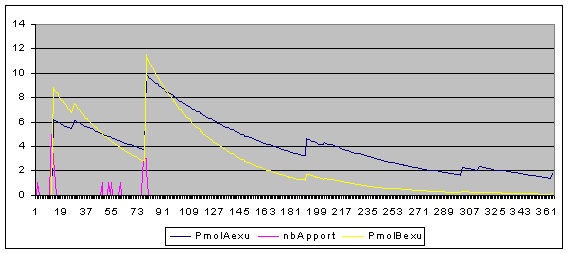
Figure 13: simulations of amount of two kinds of pesticides at the outlet in a depression landscape (in pink are number of farmers supplying pesticides each day)

8.3.2 Results claimed as significant

First results on simulations seems to show a threshold effect of rate of ditches among borders. If there are more than some 30% of borders as ditches then pesticides go in big amount in river while if it is less than 30% a few pesticides go to the river. Validation has still to be done but this non linearity of the response is an interesting result.

8.3.3 Methodological Lessons

Co-design of model entails reaching interesting models which may be used to simulate scenarios. They facilitate the choice of a right scale for representation.

8.3.4 Future Development

The process is going on with the co-design process with major stakeholders up to the point of diffusion to resource users.

Simulation of scenarios on communication among farmers and sensitivity analysis is next step to understand the effect of social processes within various landscapes patterns.

8.3.5 Published works relevant to the model

Borderelle A.-L. (2002). Eléments pour une modélisation théorique destinée au partage de connaissance. Exemple de l’utilisation des produitsphytosanitaires en viticulture sur la ressource en eau. Mémoire de DEA, ENGREF/Université de Montpellier 2, Montpellier.

9 The Maaswerken negotiation model

Joerg Krywko; Pieter Valkering, Jan Rotmans, Anne van der Veen, ICIS

9.1 Modelling Context

Description Domain Context

The model tries to reflect on a negotiation situation related to planning efforts in the Maaswerken project. The large-scale infrastructure project was started in 1997 to integrate two main projects ''Grensmaas'' and ''Zandmaas/Maasroute'' with the problems of flood protection after the two severe floods of 1993 and 1995. The foundation of the Maaswerken project as well as the Maaswerken organisation was intended to cope with the complexity of problems and issues, and the plurality of stakeholder interests in the planning region. The course of the project has been changed, since planning began in the early 1990's without taking the thread of possible floods in account. Yet, the main criteria of the project are:

1) improvement of flood control,

2) development of new nature areas,

3) improvement of the navigation infrastructure on the Zandmaas and Juliana canal,

4) gravel extraction

The planned measures to achieve these goals are:

Deepening and broadening the summer bed of the river, lowering the flood plains, creating new side canals (in the winter bed), building embankments and renew the sluices. This entails a fifth criteria:

5) hindrance during the execution period of the project

The planning procedure consists of the submission of planning proposals by the Maaswerken organisation, the objection by the public, and the repetition of both processes until a compromise is found. The latter process is main subject of the (ABM) modelling endeavour. An elaborate description of the domain context is available in the Maastricht part of the WP2 document.

9.2 Original Purpose of Model

The purpose of the (coupled) integrated assessment model and agent-based model is not to predict processes in a real world example as the Maaswerken. However, due to a shift from mono-centric decision making to a polycentric understanding of policy making in water management there is a higher demand of incorporating stakeholder positions in planning procedures. Therefore, the model is an attempt to incorporate social dimensions like stakeholder interests, goals and pluralism in terms of a variety of stakeholder perspectives. Furthermore these dimensions are supposed to be modelled in a way to simulate negotiations between various stakeholders in form of agents. There are three main objectives:

1. Analyse and reconstruct the course of the Maaswerken project on an organisation level. In other words we try to find a way to describe the negotiations between organisations that represent stakeholder interests in form of an agent-based computer model.

2. Explore possible future "pathways'' of the Maaswerken. Which planning strategies are most sustainable, and what are the (long-term) consequences on the environment as well as on the agents (stakeholders) within the target system?

3. Identify robust strategies taking in account the most significant uncertainties and stakeholder perspectives. Both are highly inter-connected since every individual or organisation has its own view (belief) on how the world works. The incorporation of both landuse scenarios and climate change scenarios within simulations help to identify uncertainties stemming from physical processes of the environment.

9.3 How was the Model Actually Used

The model was used to describe the planning processes of the Grensmaas project by entering 5 different "real world'' planning approaches (''Groen voor Grind'', ''Maasvarianten 1-3'' and the most recent proposal by the province of Limburg). The planning proposals have been generalised to strategies consisting of a set of measures in relation to a cross section. The cross section itself has been generalised from a two-dimensional model indicating measures on various locations along the river. In the beginning the model was used to test the sensitivity of the physical environment to the impact of planning strategies.

The model is basically tailored to the needs of water managers who want to decide on a set of measures, forecasting the impact of these measures on the environment as well as on the goals and needs of various stakeholders.

The model can be used as a communication support during a negotiation. Stakeholders are modeled as independent and cognitive computer agents, and they are at the same time enabled to manipulate model parameters related to their own goals and beliefs. After each simulation run stakeholders may monitor the results and see the consequences of their actions, respectively their reactions.

The targeted users are water managers and decision makers on one hand, and involved organisations and institutions like citizen groups, municipalities, NGOs and Farmer organisations, who have been consulted during a serious of interviews on the other hand.

The impact of planned changes on the environment can be tested by help of a local example in form of a cross section. This helps to understand the model relations between agents and the environment as well as possible feedbacks of human impact on the environment.

9.4 Relationship to other Models

The physical model in its current phase has the capability to calculate dynamics of the physical environment. All modules and their relationships are newly designed. The ABM design is based upon real world observations (planning documentation of the Maaswerken organisation) and concepts from social psychology (Conte & Castelfranci, 1995), conflict and attitude research in sociology.

The physical models are based upon known mathematical models.

9.5 Model Design

Intended interpretation

The model has a descriptive character. It is supposed to reflect the planning procedure of the Maaswerken project. In principle, this consists of interactions between a policy maker proposing planning strategies and other stakeholders (in the model both are represented as agents), evaluating the proposed strategy, and displaying agreement or disagreement (see Figure 14).

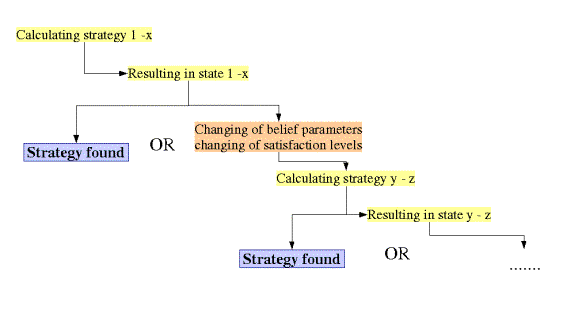
Figure 14. Negotiation scheme of Maaswerken agents

The agent policy maker is able to propose plans that suggest a set of measures (strategy) that change the environment. Therefore, this agent is able to perceive the current environment (state (0)), and perceive the respond of other agents. Based upon this information the agent 'policy maker' creates a strategy, that may lead to a new state of the environment. The magnitude of impacts of these measures can be calculated by the integrated assessment model. The results are perceived by the other agents. The respond will be reported to the policy maker agent. This process will be repeated until a compromise is found (see Figure 15).

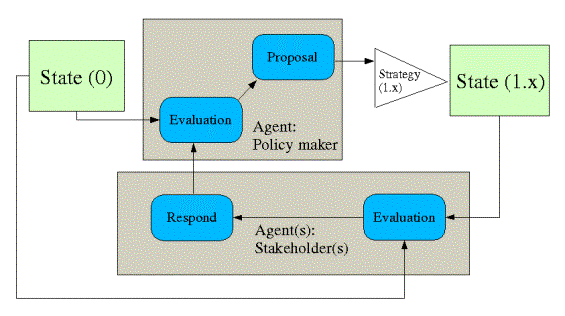
Figure 15. Finding a consensus strategy

The Integrated assessment model is able to calculate the impact of the planning strategies on the environment.

Agents in the model represent stakeholders in the real world. More specific, agents represent stakeholder organisations. The emergence of these organisations from single individuals has been observed, and is now assumption for further modelling.

The agent architecture is based upon concepts originating from concepts of social psychology. The objectives of organisations and their knowledge (belief) is modelled by help of the symbolic representation 'goals' and 'beliefs' (see Figure 16).

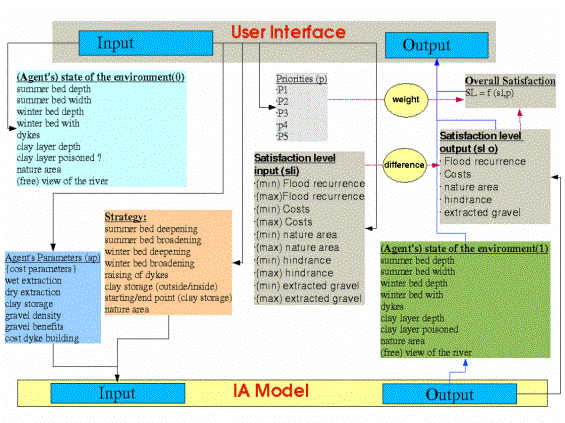
Figure 16. Agent architecture

In the model the agent system comprises four stakeholders. These are: 1) the citizens, 2) the gravel extractors, 3) the nature organizations and 4) the policy maker. These agents act on the basis of five indicators from the physical environment: 1) the recurrence time of floods, 2) the monetary costs, 3) the area of nature, 4) the amount of hindrance, and 5) the amount of extracted gravel.

The criteria are identical with goals and can be expressed in quantitative values. Thresholds indicate whether or not an agent agrees with a planned measure. Threshold values can be displayed by help of satisfaction level curves indicating minimum and maximum values as well as the 'negotiable' values.

Priorities among goals help each agent to display an overall assessment relating to all interesting criteria. A system of weights helps to set priorities and come to an overall assessment.

Besides the agent architecture Figure 16 shows the interface of the agent module to the integrated assessment module and the user interface (see Figure 17) as well as the data flow between them. The difference between the two agent types is best described by the use of the model. The policy maker is enabled to modify the strategy class.

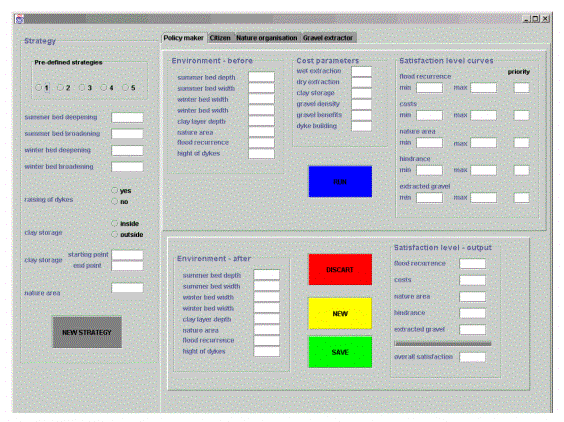
Figure 17. User Interface

The user interface enables the stakeholders to insert their own parameters, and displays results that can be interpreted as consequences of an implemented strategy. Own beliefs of stakeholders in form of cost parameters are included within each calculation.

The actions and reactions of agents are represented as 'history' (the memory of former actions in a table). After a number of proposals, each stakeholder may change values of elements of the symbolic representation. This can be part of a participatory group meeting.

The interaction and communication between agents is modelled by a communication protocol (e.g. the number of action proposals is determined as well as the number of sequences of proposals). The aim is to achieve a 'master plan' of changing the nature without violating principle goals of (stakeholder) agents, as well as achieving a ustainable state of the environment.

In the prototype model the environment is represented by a river cross section (see Figure 18) with a standard length of 500 m. This way the planned changes (strategies) on the environment can be modelled in a simplified way.

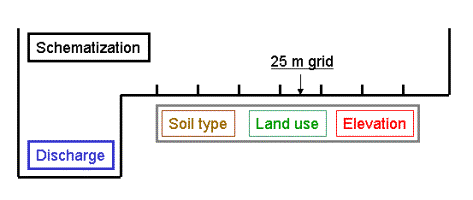
Figure 18. Cross section

The physical model consists of a number of modules and their relations.

The 'load strategy' module corresponds with a planning proposal. It is capable to update those files describing the environment (hydraulic schematisation, river sections, DEM, soil and land use files). The module contains 8 numbers representing following measures:

· Summer bed deepening (m)

· Summer bed broadening (25 m units)

· Winter bed deepening (m)

· Winter bed broadening (25 m units)

· Raising of dikes (m)

· The option between:

· Storage outside the region after cleaning (1)

· Clay storage within the area in a clay shield (2)

· The starting point of the clay shield (25 m units),

· The width of the area along the river that is allocated to nature (25 m units).

Three primary aspects of the discharge pattern can be calculated with the Rainfall-Runoff module:

1) the recurrence times of extremely high discharge (Gumble analysis and the conditional peak method),

2) the exceeding times of regular discharges, and

3) the average spring discharge.

The hydraulics module calculates the relation between the discharge and water level. The only input to the module is the schematisation file to represent the river cross-section.

The groundwater module calculates the groundwater table along the river on the basis of the average spring discharge calculated with the rainfall-runoff module and of the soil characteristics of the adjacent land.

The inundation module calculates the inundation duration for each grid cell. The critical height where flooding occurs is in principle equal to the elevation of the grid cell.

The flood risk is calculated as follows:

· The ''critical'' height of which flooding occurs is determined. In general, this will be the height of the grid cell of land use type "inhabited area'' closest to the river, possibly raised with the height of the protecting dikes, as specified by the elevation file. If no inhabited area exists, the module takes the elevation of the bank of the winter bed as the critical height. When no winter bed has been created, it takes the elevation of the bank of the main channel.

· The "critical discharge'' corresponding to this "critical height'' is determined from the discharge water level relation produced by the hydraulics module.

· The frequency of occurrence of the "critical discharge'' is determined from the recurrence times of extreme discharges produced by the inflow module. The recurrence time of floods is specified in years.

The flood damage module calculates total monetary damage as a result of flooding for floods of different recurrence times. This is done on the basis of the damage functions and maximum economic values (EURO/ha) of different land use types found in (V&W, 1999)

The nature module simply calculates the area of nature by summing all the grid cell of land use type "nature' This number is multiplied with the cross-section length and the length of a grid cell, so that the result is specified in m².

The costs module calculates the extracted volumes and the cost and benefits on the basis of the three soil files: before measures, after measures excluding clay shield construction, after measures including clay shield construction.

Hindrance is calculated as follows. The module scans the grid for cells with land use type "inhabited area'' (code 50). For each of these grid cells the hindrance is calculated by summing "sub hindrances'' over a surrounding length of 20 grid cells (10 in the direction towards the river, 10 in the direction away from the river). When the surrounding length overlaps with the river or with the other area boundary, the surrounding length is automatically shortened to fit within the region. The "sub hindrances'' equal the total volume of extracted material, multiplied with the two constants: 1) the number of people in each "inhabited'' grid cell, and 2) the total number of days of extraction is needed to extracted 1 m³ of material. The "sub hindrances'' are weighted with the value of the distance between the grid cell of inhabited area and extraction. The total hindrance is calculated by summing the hindrances of all grid cells of land use "inhabited area''.

9.6 Static Structure

The number of agents is constant. If this number must change, the model has to be expanded by a new instance of class agent. Emerging agents or group agent are not programmed. The agent architecture is in principle static. Each agent has goals, beliefs (symbolic representation) and an action plan.

The communication structure between the agent is static (see Figure 14). The interaction protocol determines how the agents interact with each other. The interface between the agent-based model and the integrated assessment model is static as well as the user interface.

9.7 Temporal Structure

The values of parameters determining thresholds (of each agent) are variable and may change under conditions. This may be changed by stakeholders. Belief parameters can be changed in the same way. An agent may also choose between different methods in calculating environmental parameters. Reasons for changing methods, however, have to be predefined, and may also change under conditions.

In a planned version of a simulation model under changing climate and land use condition, the dimensions of the environment can be dynamic.

9.8 Important Parameters

Important parameters can be expressed in the "strategy" or planned measures:

Summer bed deepening/broadening, winter bed deepening/broadening determine the parameters determining the riverbed geometry. These measures, as well as raising of dikes, establishing an area devoted to nature and clay storage correspondent with the so-called "belief" parameters of an agent. An agent wants to change the world according to his own ideas, for individual reasons. Therefore the variety of these parameters express different perspectives on the world.

Another set of important parameters is goals, expressed in threshold values. Besides the priorities these parameters determine the acceptance of proposed strategies. Every agent is able to compare parameters from its own set of goals with the parameters of a proposed strategy. This way the agent is can react with "no", if the lower limit is not reached, with "to be negotiated", if the proposed value is higher than the minimum value, but lower than the maximum value, and "yes" if the maximum value is reached. The maximum value in fact means that a minimum value is reached for an unconditioned agreement.

Priorities of an agent determine the order of goals of an agent.

9.9 Initialisation

A simulation is being started by an initial strategy that is inserted by the policy maker. This is taken from the Maaswerken reports. The relations of measures of real world data are reference for relations in the modelled target system. The sequence of the strategies is determined by the applied communication strategy.

9.10 Implementation Language

The implementation language is C++. A more recent agent module is currently being programmed in Java.

9.11 Source Code

The source codes can be downloaded from

ftp://exchange@ftp.icis.unimaas.nl/Firma/

password: icis

9.12 Conclusions

The model consistant of an agent module, an environmental module and a user interface is able to display the consequences of the impact on the environment in combination with various beliefs and goals of stakeholders. The latter fact is possible due to independently working agents who observe the same measures on the environment, however, reseive different results. This is only possible, because of incorporating the agent's individual symbolic representation in the simulation.

Planners and decision makers are able to see the consequences of their planning strategies not only on the environment, but also on the interests and goals of involved stakeholders. The interface serves as comunication tool for a stakeholder meeting. The advantage of this model approach is a quick test of a number of strategies that can be discussed within a time period of a stakeholder meeting. Decision makers are able to reconsider planning strategies, stakeholders are able to reconsider their own beliefs and goals, based upon an integrative modelling strategy.

9.12.1 Example Simulation Output

Figure 19. Example simulation output

Figure 19 displays results based upon two different events. The first part shows a strategy with a low safety level. The agents 'citizens' and 'policy maker' disagree with the strategy because of a low safety level. (overall satisfaction 0). The second part shows a higher belief parameter 'gravel density' adopted by gravel extractors. This strategy is still declined by gravel extractors because of the high net costs.

9.13 Methodological Lessons

A target system like the Maaswerken project requires a simplified prototype model to detect in principle model relations on one hand and the complexity on the other.

Using concepts origin from social psychology appears to be an appropriate way to simulate communication between cognitive agents. However, applying these methods entails a high degree of uncertainty. For example, assuming organisations act based upon rational decision making is reasonable in theory. However, irrational elements in decision processes can not entirely excluded. The modeller has to take in account non-linearity of decision processes, which can not be modelled at the moment.

9.14 Future Development

The model will primarily be used by water managers. The aim is to support planning processes by adding perspectives of various stakeholders to the model. This way the consequences of actions on the nature as well as on other agents can be made explicit.

A final validation discussion still has to be performed, to tailor the model to the specific requirements of the modelled stakeholders.

In the moment the model is based upon a simplification of agents as well as on a simplification of the environment. This entails unavoidably scaling problems. Measures taken upon the environment take place on various location along the river, with mostly local impact on residents and nature. This must be improved in a further developed model. The environment has to be modelled two dimensional to give way for implementing specific measures. Simultaneously, the number and the specification of agent has to be increased.

Hoever, the overall approach shows a way to avoid a mere 'engineering solution', enabeling collaborative planning approaches.

The model should, furthermore, encourage people to participate a discussion about a project without a specific knowledge of engineering or planning procedures. It should also give the user insights to consequences of the impact on nature and possible reaction of other stakeholders as well as limitations emerging from a negotiation process.

9.15 References

Conte, Rosaria, and Cristiano Castelfranchi (1995) Cognitive and social action. UCL Press limited. London. 215p. ISBN 1-85728-186-1

9.16 Published works relevant to the model

Krywkow,J., Pieter Valkering, Anne van der Veen, Jan Rotmans (2002) Coupling an Agent-Based Model With an Integrated Assessment Model to Investigate Social Aspects of Water Management. In: Christoph Urban (Editor) Workshop 2002: Agent-Based Simulation 3, Proceedings, SCS-European Publishing House, Erlangen, Ghent 2002 ISBN 3-936150-17-6 http://www.or.uni-passau.de/workshop2002

Krywkow, J., Pieter Valkering, Jan Rotmans, Anne van der Veen (2002) Agent-based and Integrated Assessment Modelling for Incorporating Social Dynamics in the Management of the Meuse in the Dutch Province of Limburg. In: Rizzoli, A.E., A.J.Jakeman (Eds.) Integrated Assessment and Decision Support Proceedings of the First Biennial Meeting of the International Environmental Modelling and Software Society, vol.2, p 263 - 268. IEMSs 2002, 24 -27 June 2002, University of Lugano, Switzerland. ISBN: 88-900787-0-7. http://www.iemss.org/iemss2002/proceedings

Valkering, P. (2002) Prototype 3. Working paper ICIS.(in press)

10 Metropolitan Area- Model for the Barcelona

Adolfo López-Paredes, University of Valloid

David Sauri, Universitat Autonoma de Barcelona

10.1 Modelling Context

10.1.1 Description Domain Context

The main objective of this project is the development and the application of agent based models integrating physical, hydrological, social and economic aspects for the improvement of drinkable water resource management.

To make it possible we have designed a model that integrates different modules. Inside these modules we find the consumers, municipalities, institutions, the companies and the climate. The modular structure has the advantage of allowing us to develop the different submodels of the system (social, climatic, economic...) in an autonomous way and presenting different levels of disaggregation. Each one of them is a model formed by agents and integrated in a superior range entity that facilitates the mutual interactions of the participants of the system.

Methodologically, we have used agent based modelling to develop the model. The model has been designed to enable the micro-definition of the agent’s behaviour at level of the individual but with the final objective to understand global societal phenomena. That is, the aim to understand the emergence of macro behaviours resulting from micro-level interactions.

10.1.2 Original Purpose of Model

This model's purpose is to build a tool that allows us to study and to test the effects of alternative policies and strategies of water management in the Metropolitan Region of Barcelona. These policies can be oriented toward supply policies and/or demand policies. From the point of view of the demand, we compare different strategies of prices. From the point of view of the supply we evaluate different infrastructure policies.

It is interesting to analyse the effect of these policies with different weather conditions, different sequences of precipitation and temperatures in the region. So we can distinguish the influence of environment in evaluating those policies.

10.1.3 How was the Model Actually Used

The model has been implemented with two languages. The SDML version has been intended to create the structure and check the results of simulations at low scale. The Java version has been realized with the SDML structure, but a greater scale, close to the real system we are studying. Currently we are working in calibrating the parameters of the Java version.

10.1.4 Relationship to other Models

The growth of the metropolitan region is inspired in the Schelling model of spatial organisation of cities. The evapotranspiration concept employed in the SDML model of Thames Region has been performed for the Barcelona Region.

10.2 Model Design

10.2.1 Intended interpretation

The model is intended to facilitate discussion between stakeholders. The program is designed to run the simulations in an interactive mode. So, stakeholders can introduce their preferred strategies to compare the effects on the global system. The model can not be used as a forecasting tool and discussion should address the dynamics of different management policies.

10.2.2 Original Sources for Model Design.

We developed the core model from the stakeholders’ beliefs on water consumption. Some modules in the model has been designed from other models: the works of Benenson and Schelling on population distribution, and the market’s model of Galan.

10.2.3 Static Structure

The model has been built on different submodels. These submodels interact with each other and with the user[3]. The different modules that compose the system are the following ones:

Social Module: In this module the families perform their social behaviour, the processes of birth, growth, emancipation and death of the family members, the immigration process into the region, and the process of the individuals' decision to move house.

Territorial Module: This module deals with the initialisation of the different municipalities, of the distribution of their houses and of their expansion through time.

Climate Module: This is in charge of collecting the data of precipitation and temperatures introduced monthly in an exogenous way to the system, for access by the other elements of the system.

Water Demand Module: This is the module responsible for obtaining the desired demand of each family and of determining the real consumption of each one of the water consumer agents in the model, to build the aggregated demand of drinkable water.

Infrastructures Module: Module in charge of holding and updating the group of infrastructures of the region during the simulation.

Supply Module: This module obtains the information from the climatic module and the module of infrastructures in order to determine the regional supply water.

Stakeholder Module: This module includes the rest of the agents or institutions that participate or have influence in the water process. Here there are agents like Municipalities, Generalitat, and water companies. These agents are modelled by means of the price strategy and the infrastructure policy.

Emergency flag: This is a simple bit that is active when there are problems in satisfying the demand of water with the available supply at a given moment. Its state influences the agents’ consumption decisions.

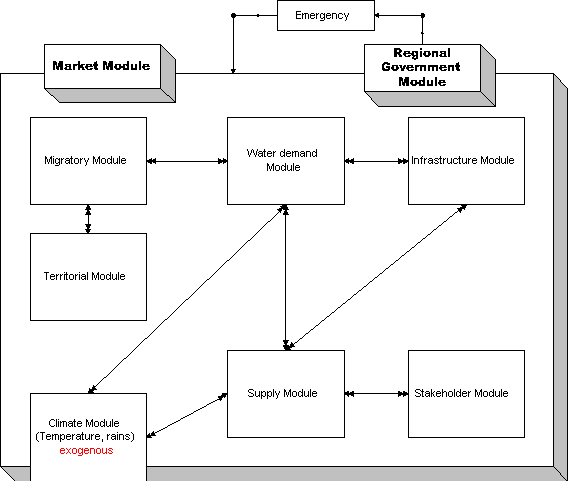
Figure 20. General diagram of the model.

10.2.4 Important Parameters

There is a list of initial parameters whose values should be carefully addressed to avoid abnormal results in simulation. These are explained in the appendix 1.

10.2.5 Initialisation

Once all the parameters are fulfilled[4] and we start the simulation, the initialisation stage of the model states:

1. The first thing that takes place in the simulation once the execution begins is the creation of an instance of the climate module. This instance holds the list of precipitation and temperatures of every month along the whole simulation. These data are provided with two ASCII files called Temperatures.txt and Rains.txt and they are kept in memory by means of two lists to be requested by the simulation when some object needs them. The climate module controls this step.

Figure 21. Text file to introduce temperatures of every month.

2. When the data of the climate have been loaded in memory, the program reads the variables worldXsize and worldYsize that determine the window corresponding to the geographical area of study (Territorial Module).

2.1. A reticular surface to hold an object in each of their places. It will be in charge of holding the houses of the municipalities of the region.

2.2. Two reticular surfaces of the same size as the previous one and they will take charge of holding values, one will hold the demand in each place and the other one the predominant social class.

3. After this, the following step is the construction of each one of the municipalities according to the values that we have defined in the configuration windows. In order to construct it, the simulation reserves the defined space of each municipality in the grid (reticular surface) and begins to build their houses. (Territorial Module)

3.1. The initial construction of the houses of each municipality is done through going all over each one of the cells that belong to the surface define by the coordinates x1, x2, x3 and x4 and creating in each cell a house type according to the percentages probSemiDetached, probFlat y probUnifamiliar defined in the parameters of each Municipality. This way, the initial configuration of houses of each municipality is obtained, formed by flats, semi-detached houses, detached houses or unbuilt zones.

3.1.1. Each one of these constructions has their own variables that characterize it, such as their situation in the grid, the maximum number of families that can inhabit it, a list of current family locations, their price or the housing type.

3.2. After the simulation has created the houses, it builds the initial number of families in each municipality. These families are created with random internal variables according to the parameters defined in the configuration windows FamilyParams and the characteristics of each Municipality.

3.3. When the program already has the initial number of families that has been defined, the following step is to allocate houses for those families. In this distribution process, each family chooses, in turn, a house. If the family has enough wealth to buy it and if there is available place, the family buys the house and begins to live there. If not, the family repeats the process until it finds a place to live. If after a high number of attempts (2000) a family has not found a house, then it becomes part of the families that rent a house in the municipality, and it will try to move up to owning a house in the future.

4. The particular supply is created; the group of infrastructures that hold the supply of water in the whole region. This, in turn, creates the instances of desalination plants and reservoirs (defined in Supply Window) in the region. In addition, the simulation introduces specific water leaks that appear because the use of the net and because different dissipater effects, WaterLeak. (Infrastructure Module).

4.1. The reservoirs are characterized by their cost, their maximum capacity, their surface, and by the cubic meters that are contained in a certain period of time.

4.2. The desalination plants are characterized by their cost and by the cubic meters of water that they are capable of desalinating over a period of time.

4.3. The number of desalination plants and of reservoirs can be changed at any given moment during the course of the simulation.

5. Lastly a specific price policy is created, PolicyPrice. This remains in memory to be consulted by any object of the simulation at any time. This policy can be changed during the course the simulation through use of the configuration window. (Stakeholder Module)

10.2.6 Key Algorithms

The migration processes.

Computing water price.

Computing familiar water demand.

10.2.7 Description of Model Dynamics

We differentiate two time levels in the model: month and year. Agents act at these time levels:

Monthly events:

1. The temperature and precipitation values. (Climate Module).

2. The reservoirs store a percentage of the precipitation depending on their surface and maximum capacity. (Infrastructures Module). Desalination plants provide a quantity of available water. (Supply Module). The program calculates the losses in the water net and they are discounted from the water supply. At the end of this the available water in this period is known. (Supply Module).

3. The social module that contains the migration module is executed. This step includes the social development of the families, immigration and moving (Social Module). When families decide to move, their decision is affected by: price, social class and family size, as follows.

Price. We define the neighbourhood of a family’s house as the collection of the houses that are adjacent to it. The family calculates the mean house price of such a neighbourhood using the Equation 1. The simulation calculates the price of the neighbourhood of the three candidate houses and of their own home in this way. To normalize the data, all of them are divided by the highest price and multiplied by the weight with which each family values this first effect. In this way the simulation obtains the first factor that allows the valuation of each house by a family.

Equation 1

Figure 22. Diagram of a neighbourhood.

Social class. The second factor to value a candidate house is the number of people of the same social class that inhabit in the neighbourhood of the candidate house. To make it, each family finds the percentage of families of the same social class in the neighbourhood of each house, and all these data are normalized in similar way to the previous step. This it is the second criterion that allows valuing the suitability of the houses.

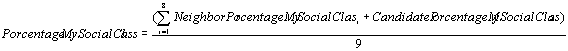
Equation 2

Family size. Depending on the number of members that are members of a family in a given moment, each family will have a preference for a house type or another according to the Table 1. After a family has pondered the preference, the simulation works as in the previous cases, divides by the highest number to normalize and multiplies by the factor of influence of this effect on this particular family.

Family size	3	2	1
1-3	Flat	Semi-Detached House	Detached House
4-5	Semi-Detached House	Detached House	Flat
> 5	Detached House	Semi-Detached House	Flat

Table 4. Preference for house type according to number of members in the family.

Once each family has quantified the three influence factors relating to moving, it chooses the suitable house according to the Equation 3.

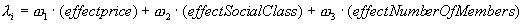
Equation 3

Where

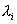· is the value of the i-house for a family.

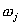· are the weights different that each family gives to the different effects.

· effects are the normalized values of each candidate house.

The birth of new members in the family. Depending on the cycle of family life, there is a certain possibility that a family has a new member. This probability is more intense in the first ten years of life of a family, a little lower until the twenty years, and impossible from then on.

The possibility of emancipation . To model this effect, all the families of each municipality are analysed; those families that have children of an age between twenty and forty years have a probability that a child will leave home. The simulation put the list of emancipated children into couples to form new families. Those families initially begin living in rented accommodation, waiting to buy a house in future iterations. The characteristics of the newly created families are not random. They are consequence of the couple's inherited characteristics that have formed this new family.

After emancipation, the immigration effect occurs according to the parameter ratePopulationGrowth. The population of each municipality increases proportionally to the value of the parameter specified in the window of configuration of each municipality. These new immigrant families are formed randomly according to the parameters defined in the municipality and they initially also begin living in a rented house.

The families that rent try to buy a house. Each family tries to move to any place inside the region with the only conditions being having enough money to buy the house and of having enough space in the house for the family. Each family tries that every iteration. With this step, we finished the execution of the social module.

4. Agents establish their consumption desires for that period. (Water Demand Module).

4.1. Consumption desires are a function of factors like the social class, the housing type, number of members in the family and whether we are in an emergency situation or not. With all these factors we determine an initial number of irrigation, showers, washes and WC uses for that month.

4.2. These initial values are modified by a "remember factor" of the consumption in the previous month. The families store their consumption in the previous period, if this consumption was higher than the current desires, their consumption desires increase, but however, if this consumption was inferior, they don't modify it. This factor is an effect of asymmetric inertia about consumption desires that enables its growth.

4.3. Lastly, to complete the determination of the consumption desires of each family there is an imitative effect among families. The families interact among them choosing several (three) of them inside their neighbourhood, and watching their consumption in the previous period. If the consumption of its neighbouring families was higher than its own, they perceive it as “free rider” behaviour and they try to compensate for it by increasing their own consumption desires. On the other side, if the consumption of the neighbouring families was lower than the own, they try to modify their consumption habits to adapt to the predominant social behaviour in the vicinity. When this step finishes, all the families know their consumption desires for the period.

5. Once the families know their consumption desires for the current period, they adapt them to their economic reality. Each family is willing to pay randomly between 2-3% of their annual incomes for the consumption of water as a maximum. The families compare their consumption desires with the policy of prices that is active in that period, if their water expense is lower than the limit that they set for themselves, their real consumption will coincide with their consumption desires and they won't be dissatisfied as regards water. However if their consumption exceeds their budget, they will reduce their expense so that it doesn't overcome the limit. In this case the agents will increase their "unhappiness" in the cubic meters difference between their desires and their reality. (Water Demand Module).

6. When all the families know exactly their water expense and the extent of their dissatisfaction, the program aggregates the demand. (Water Demand Module).

7. The program evaluates if the region is in an emergency situation due to water scarcity. (Emergency Flag)

8. The indexes of occupation by housing type of each municipality are calculated. (Territorial Module).

9. The wage corresponding to each family is added to its accumulated wealth. (Social Module).

10. The expansion of the municipalities takes place. We divide the possible expansion of the municipalities in 8 regions, each one of them with a housing type assigned by municipal plan. In the step 8 the simulation had already calculated the different occupation indexes of each municipality for housing type. If some of them exceed a certain value, those regions with types of assigned housing equal to those of high occupation index grow. This growth takes place inversely with a function of probability proportional to the distance to the initially built municipal area.

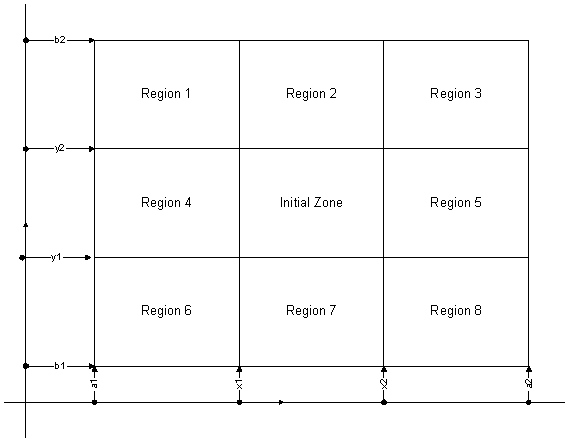
Figure 23. Diagram of the regions that are defined in a Municipality.

11. The program executes the process of the population's death. A similar process for the birth or the emancipation is used. Each one of the existing families is analysed, and in those families that have more than 40 years of life, there is a probability of death of some of their members. When a family doesn't have any member that family disappears and it leaves its house empty.

Family’s age	Born	Home Leaving	Death
0-10	Prob++
10-20	Prob++
20-30		Prob--
30-40		Prob--
40-60			Prob--

Table 5. Synoptic chart of the family evolution model.

Annual steps:

1. The only annual action that is executed in the program is the increase of the price of the housing of each municipality depending on the index of occupation of the municipality. If this index is lower than a certain value the price of housing doesn't increase that year, in the contrary case, the housing price increases in the proportion to the parameter growthHousingPrice. This process tries to make the market in real estate into an endogenous process.

10.2.8 Implementation details necessary to get the simulation to run but not considered important for the results

There is a complete model of migration and population distribution in the region that is intended to ascertain the effects of the territorial change happening in the metropolitan region of Barcelona. This model could be used for similar studies with other goods: electricity, gas, public transportation, etc.

There is also a module where different water prices are computed depending on whether water is considered a pure public good, a pure economic good suitable for a market price, or a mix of those. This module is used to evaluate in an objective way the effects of different price policies.

10.2.9 Implementation Language and Source Code

The final version suitable for stakeholders’ use has been implemented in Java. Notwithstanding, this version has been built based the SDML version, which is more appropriate for pure qualitative analysis and a better understanding of the model.

Language: Java 1.3.1- b24

Environment: JBuilder 6

Platform: PC

Libraries: JFreeChart, Swarm

Source code available: adlo@eis.uva.es

Documentation:

Developers: Adolfo López, José Manuel Galán

Language: SDML 3.4.c

Source code available: adlo@eis.uva.es

Developers: Adolfo López

10.3 Conclusions

10.3.1 Example Simulation Output

In this section we show some of the most significant windows that give information about model. All the windows are very intuitive, and they seek to reflect most of the outstanding information in the model.

Changes of Citizens. This window shows the number of people who sell/buy their house in every municipality of the model. This chart analyses the numbers of movements in the migration module.

Figure 24. Number of citizens moving across municipalities.

The Region. This window shows a map in which every municipality and every housing type is represented with a colour code.

1. Red.- A flat.

2. Yellow.- detached house.

3. Green.- semi-detached house.

4. Black.- A cell without building.

Figure 25. Map of the municipalities.

Social Class. This window is a map of the grid that represents the majority class of each house. The colour code of this is as follows:

1. Red. - High class.

2. Yellow. - Low class.

3. Green. - Middle class.

4. Black. - A cell without people.

Figure 26. Social classes distribution.

Water Demand. This window represents a map of the region with a colour code. It is the same map as the previous ones, but with different tonalities of blue. The darker blue represents higher consumption of water.

Figure 27. Distribution of water consumptions in the region.

Temporary evolution of the demand of water. It is a graph that shows the demand of water of each municipality in every period of simulation.

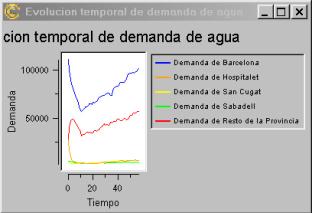
Figure 28. Temporary evolution of the demand of water.

Temporary evolution of the demand of water for housing type in Barcelona

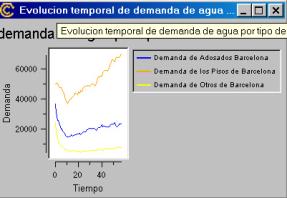
Figure 29. Temporary evolution of the demand of water for housing type in Barcelona.

People's temporary evolution

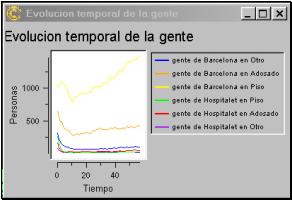
Figure 30. People's temporary evolution.

10.3.2 Results claimed as significant

Previous versions of the model were useful in stimulating and informing consultations with the water companies.

10.3.3 Methodological Lessons

Agent based modelling is suitable to improve the stakeholders’ knowledge on the dynamics that appear in the whole system in relation to the different policies. They claim realism in the model as the main basis to consider results and conclusions from the models. We assume that there are two levels of specification in agent based modelling when we develop software tools. One is intended for modellers and qualitative researchers, and can be managed through programs like SDML, Prolog, etc. The other should be adapted to user specifications with graphic interfaces, etc.

10.3.4 Future Development

Climate is not yet fully integrated in the model. More disaggregation in the human water consumption can be required by water companies. They could finance such studies to be introduced in the model/software.

Greater realism is possible through a characterization of the metropolitan region as a grid where housing is identified in a similar way to that of the model.

10.3.5 Published works relevant to the model

Not yet

10.4 Appendix I. Configuration of the simulation.

When we execute the program a first standard window is displayed. This window gives us the general options for the control of execution of any simulation. These options that are offered are five:

Ø Start. When we press this button the simulation begins.

Ø Stop. When we press stop, we stop the execution, but if we pulse in Start again we continue the execution.

Ø Next. The program executes a complete period of the simulation and stops. It is good to execute a simulation step by step.

Ø Save. To record a simulation.

Ø Quit. We leave the simulation, end of the execution.

Figure 31. Window of control of execution of the process.

When this window appears, also other windows also appear to give us information about the simulation, and to allow us to configure it. We will explain the functionality of each one of these windows.

ModelSwarm. This window is a probe to the model, and it allows us to configure the most important parameters in the simulation.

The window contains variables in array, with the name of the variable in the left part and with a changeable cell where we can introduce the value more interesting of the variable on the right.

The different parameters that we can control in this window are:

· worldXSize: The number on cells in X-dimension in the grid.

· worldYSize: The number on cells in Y-dimension in the grid.

· endTime: period of finalization of the simulation..

· probMigracion: migration probability.

· totalUnhappiness. It is the total unhappiness of all the citizens in a period of time in unsatisfied m3 of water.

· moneyCollected. It is the quantity of money collected due to water consumption. The money spent in infrastructures is also entered here.

· emergency. This parameter determines percentage of the total capacity of accumulation of water under which the region is in an emergency situation.

· emergencyFlag. It is a boolean variable with two possible states, false, if we are not in an emergency situation and true if we are.

Figure 32. ModelSwarm window.

Ø ObserverSwarm. This window controls general parameters related with the way of representing the data collected in the model. It is a window that allows us to configure the Observer.

This window controls the following parameters:

· displayFrecuency: this variable determines each how many periods we want to pick up information on the model

· zoomFactor: this variable allows to configure the size of the window “The region”.

· zoomFactor2: this variable allows us to configure the size of the window “Water Consume”.

· zoomFactor3: this variable allows us to configure the size of the window “Social Classes”

Figure 33. ObserverSwarm window.

Ø FamilyParams. This window allows us to configure the general parameters of the families that participate in the model. These parameters, are the following ones:

· highClassMaxWage: wage annual maximum of a high class family.

· highClassMinWage: wage annual minimum of a high class family.

· lowClassMaxWage: wage annual maximum of a low class family.

· lowClassMinWage: wage annual minimum of a low class family.

· mediumClassMaxWage: wage annual maximum of a medium class family.

· mediumClassMinWage: wage annual minimum of a medium class family.

· highClassMaxInitialWealth: initial wealth maximum of a high class citizen.

· highClassMinInitialWealth: initial wealth minimum of a high class citizen.

· lowClassMaxInitialWealth: initial wealth maximum of a low class citizen.

· lowClassMinInitialWealth: initial wealth minimum of a low class citizen.

· mediumClassMaxInitialWealth: initial wealth maximum of a medium class citizen.

· mediumClassMinInitialWealth: initial wealth minimum of a medium class citizen.

· probSolidarityAttitude: Percentage of families with solidary attitude that reduce their demand when there is an emergency situation.

· weigthMyHouseAgainstMyNeighborhood: The weight of my house against that of the rest of the neighbourhood to calculate the mean price of the neighbourhood .

Figure 34. Window of the parameters of the families.

Ø Municipality: This window allows us to configure the general parameters of each municipality in the simulation. Each one of the municipalities possesses their own configuration window, in such a way that a window is displayed for each municipality in the model.

The parameters in this window are the following ones:

· name: Name of the municipality.

· x1: Initial situation coordinate of the municipality in the grid.

· x2: Initial situation coordinate of the municipality in the grid.

· y1: Initial situation coordinate of the municipality in the grid.

· y2: Initial situation coordinate of the municipality in the grid.

· a1: Coordinate of the maximum situation of the municipality in the grid.

· b1: Coordinate of the maximum situation of the municipality in the grid.

· a2: Coordinate of the maximum situation of the municipality in the grid.

· b2: Coordinate of the maximum situation of the municipality in the grid.

· probSemiDetached: Ratio of initial semi-detached houses in a municipality.

· probFlat: Ratio of initial flats in a municipality.

· probUnifamiliar: Ratio of initial detached houses in a municipality.

· probHighClass: Percentage of high class in the municipality.

· probMediumClass: Percentage of medium class in the municipality.

· probLowClass: Percentage of high low in the municipality.

· initialPopulation: Initial population in the municipality.

· priceMinSemiDetached: Minimum price of a semi-detached house in the municipality.

· priceMaxSemiDetached: Maximum price of a semi-detached house in the municipality.

· priceMinFlat: Minimum price of a flat in the municipality.

· priceMaxFlat: Maximum price of a flat in the municipality.

· priceMinUnifamiliar: Minimum price of a detached house in the municipality..

· priceMaxUnifamiliar: Maximum price of a detached in the municipality.

· priceMinUnbuild: Minimum price of a land without edification in the municipality.

· priceMaxUnbuild: Maximum price of a land without edification in the

· municipality.

· growthHousigPrice: Annual increase of prices of the housing in the municipality.

· ratePopulationGrowth: rate of the population's growth in the municipality monthly.

Figure 35. Configuration window of a Municipality.

Ø Supply. This window controls the infrastructures of the region. It has two probes to the variables that determine the number of reservoirs and of desalination plants, but it also has two probes to methods. These probes have two buttons that can be pressed at any time in the simulation and allow us to increase by a unit the number of infrastructures in time of simulation without stopping the simulation.

The variables that are controlled by this window are:

· numReservoirs: Number of reservoirs in the Region.

· numDesalinationPlant: Number of desalination plants in the Region.

The methods that can be executed from this window are:

· increaseReservoir: This method increases by an unit the number of reservoirs of the Region.

· increaseDesalinationPlant: This method increases by an unit the number of desalination plants of the Region.

Figure 36. Configuration window of Supply.

Ø PolicyPrice. This window allows us to control and to test different policies of prices for the management of the water and even to change the type of the policy in real time in the execution process.

Three different policies have been implemented, policy of unique price, policy of fixed cost and variable cost from certain consumption, and price policy according to consumption range.

The variables that are controlled in this window are:

· typeOfPolicy: This variable allows us to control which policy of prices is being used in a given moment.

q Unique Price

q Fixed Cost and variable cost.

q Prices depending on ranges.

· uniquePrice: Price of a m³ of water in the policy of unique price.

· fixedCost: Fixed cost of the water if you consume less than minConsume in the policy of fixed cost and variable cost.

· variableCost: Price of a m³ of water when a family overcome the limit of consumption minConsume in the policy of fixed cost and variable cost.

· minConsume: Limit between the fixed cost and the variable cost.

· section1: Limit of consumption with the rate of prices from 0 to 1.

· section2: Limit of consumption with the rate of prices from 1 to 2.

· section3: Limit of consumption with the rate of prices from 2 to 3. If a family overcome this consumption, will be applied rate of prices price_3_andMore.

· price_0_1: Price of the first range of consumption.

· price_1_2: Price of the second range of consumption.

· price_2_3: Price of the third range of consumption.

· price_3_andMore: Price of the last range of consumption.

The methods that can be executed from this window and that allow us to modify the policies of prices in time of execution are:

· strategyChange: It allows us to change the policy of prices among the three possible strategies.

· increaseUniquePrice: Increase the unique price.

· decreaseUniquePrice: Decrease the unique price.

· increaseVariableCost: Increase the variable cost..

· decreaseVariableCost: Decrease the variable cost..

· increaseFixedCost: Increase the fixed cost.

· DecreaseFixedCost: Decrease the fixed cost.

· increaseMinConsume: Increase the minimum consumption.

· decreaseMinConsume: Decrease the minimum consumption.

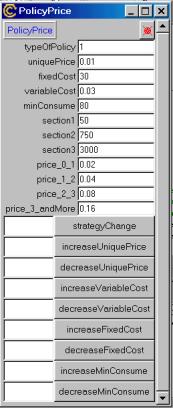
Figure 37. Configuration window of PolicyPrice.

11 Multiple Models for Participatory Modelling in the Zurich Case Study

ZWG1 – EAWAG: Claudia Pahl-Wostl, Matt Hare, Davide Medugno (no writing).

ZWG2 – EAWAG: Claudia Pahl-Wostl, Matt Hare, Davide Medugno, Johannes Heeb, Felix Huber.

ZWG3 - University of Surrey: Nigel Gilbert, Tasia Asakawa, Matt Hare, Sarah Maltby and Claire Haggett .

11.1 Domain context

The following models have been developed as a result of the group model building participatory process carried out by EAWAG to investigate how social learning can guide the future management of the water supply system in Stadt Zürich. Three implementations of the basic model have been developed. The basic model is referred to as ZWG* and is an abstraction of how the key actors (water utilities, housing associations, consumers, manufacturers and politicians) interact in relation to the provision and consumption of water and water saving products in the city. The corresponding object model and interaction diagram for ZWG* can be found in Appendix A.

11.2 Original Purpose of Model

The purpose of ZWG* is to provide a standard template for the development of three models:

ZWG1 - a computer simulation in which agents are computer automata

ZWG2 - a role playing game in which agents are played by human stakeholders

ZWG3 - a version of the ZWG2 that is played on the internet using either human or computerised agent players. This version has been developed by the University of Surrey.

The purpose of ZWG1 is to provide rapid scenario testing for scenarios generated in the participatory process. Users: EAWAG facilitators

The purpose of ZWG2 is to provide a forum for the group to explore single scenarios in depth. Since the stakeholders in the group take on roles within the game, they become actively embedded in the model, not just passive observers of it[GNG1] . It allows the stakeholders to perceive the system in its complexity from the perspectives of other players. It is also to acclimatise the stakeholders to the use of ZWG1 and ZWG3 and to validate the basic model ZWG*. Users: Stakeholders

The purpose of ZWG3 is to provide a virtual extension of the participatory process so that stakeholders can continue to explore scenarios automatically or through role playing after the completion of the project. It is also intended as a demonstration or ‘proof-of-concept’ of the idea of using business strategy games in the context of integrated assessment. Users: Stakeholders, public.

11.3 How was the Model Actually Used

ZWG2 has been used as intended. ZWG1 is in the process of being used. ZWG3 is still being tested with non-stakeholder users and has not been used with stakeholders and members of the public in a participatory setting yet.

11.4 Relationship to other Models

ZWG1 has been used to calibrate ZWG2. ZWG2 in turn has been used to elicit decision making algorithms from the stakeholders during role playing so that agent models in ZWG1 and ZWG3 can be improved.

11.5 Fulfilling FIRMA’s Objectives

The three agent-based social simulation models presented here are built upon the participation of decision-making stakeholder groups as well as experts in water resource management in Stadt Zürich. This participatory methodology includes face-to-face group communication, knowledge elicitation, role-playing, scenario testing and group model building within regular meetings of the principal stakeholders. During these meetings, multi-media (paper-, board game- and computer-based) multi-agent models of the water management system (ZWG1 & ZWG2) have been developed in order to allow the stakeholders to explore possible management scenarios and to learn about other stakeholders' often conflicting perspectives and goals. Outside of the meetings, the internet forum (ZWG3) will serve to support stakeholder interaction, model testing and the exchange of views. By drawing and these different stakeholder groups and mediums together in the modelling process, the models and their developers begin to be able to advance cooperation and understanding between all participants.

The models have assisted the analysis of water resource management in Zürich in the following areas: hydrosocial issues of water-supply; water demand; waste water treatment; water security; and the assemblage of data for agent-based modelling. The group model building process and group use of the models have shown that the hydrosocial issues in Zürich form a complex decision-making framework characterized by incomplete information, inconsistent and isolated communication networks, conflicting and inefficient institutional settings and an incompatibility between “worst-case” planning and changing consumer behaviour. These issues have been considered more closely and alternatives to current management have been investigated. More generally, it is hoped that the models and participatory methodology can help to identify particular water resource management problems/issues in a specific area and provide methods that could support conflict resolution regarding issues of water resource management.

The Zürich water game models contribute a regional integrated assessment tool to the FIRMA project. It offers a participatory methodology as well as a multiple model development process that could be incorporated into other methodologies and processes in the FIRMA or other projects for broader applicability.

11.6 Model Design

11.6.1 Intended interpretation

The model is intended to be an abstraction of the system for social learning purposes. It has been deliberately calibrated to match reality qualitatively, but not quantitatively in order to concentrate stakeholders’ discussions on dynamics rather than on quantities.

11.6.2 Original Sources for Model Design

The sources of the design came from the mental models of the stakeholders in the participatory process - through a long process of knowledge elicitation. Also from the PhD work of Tillmann (ref).

11.6.3 Static Structure

In ZWG*, there is a set of system indicators which provide the agents, the housing associations, the manufacturers, the water utility and the waste water utility and politician, with a view of the state of the system. The water utility must maintain the water supply by managing its reservoirs and keeping the water clean and gains income by selling the water to the consumers living in the housing associations (a large proportion of consumers live in rented property in this city). The housing associations in turn must maintain the water systems in the houses and are responsible for paying the water bill. It may therefore be in their interest to install water saving technologies into the houses to reduce use, since consumer demand for water is a simple function of technology used and their level of environmental awareness which can be raised through utility or political advertising. The manufacturers then enter into a market with the housing associations in which they can opt to sell normal or water saving water supply technologies. The politician must maintain the system indicators (e.g. water quality, supply) in order to remain popular enough to be re-elected every five years. He or she does this through prudent use of subsidies to the utilities, imposition of taxes and through advertising.

See also appendix A

11.6.4 Temporal Structure

A market for water saving and normal water sanitation goods is dynamically created between the housing associations and the manufacturers. The outcome of this dynamic process will affect the amount of water consumed by the houses under the jurisdiction of the housing associations.

Output variables:

· taxation income

· popularity of politician

· quality of drinking water

· quality of lake water

· environmental awareness of public

· water demand of public

· water supply to public

· water price per unit

· price of water saving water sanitation systems

· price of normal water sanitation systems

· sales of normal and water saving water sanitation systems

11.6.5 Important Parameters

Initial values of :

· popularity of politician (int: {0-10})

· quality of drinking water (int: {0-10})

· quality of lake water (int: {0-10})

· environmental awareness of public (int: {0-10})

· water demand of public (int: {0-100})

· water supply to public (int: {0-100})

· water price per unit (int: {0-100[GNG2] })

· max price of water sanitation system (int)

· maintenance costs of reservoirs, sanitation systems, factories (int)

· tax rate (%)

· demand/household lookup table (int[][])

11.6.6 Initialisation

Models are parameterised to reflect particular scenarios. Default scenario: Over capacity in a perfect world:

· popularity of politician = 5

· quality of drinking water = 8

· quality of lake water = 8

· environmental awareness of public = 5

· water demand of public = 60

· water supply to public = 100

· water price per unit = 5

· max price of water sanitation system = 750

· maintenance costs of reservoirs, sanitation systems, factories

· reservoir maintenance: 50

· house maintenance: 25

· factories: 100 (normal), 150 (water saving)

· tax rate: 10%

· demand/household lookup table:

	environmental awareness
Sanitation system in house	1	2	4	4-6	7-10
normal	10	9	7	6	4
water saving	5	4	3	3	2

Table 6. "Demand per household" lookup table.

· 1 simulation time step = 2 years.

11.6.7 Key Algorithms

a) Bargaining algorithm: housing association (HA) and manufacturer (Man) ("BargainPrice", Appendix A)

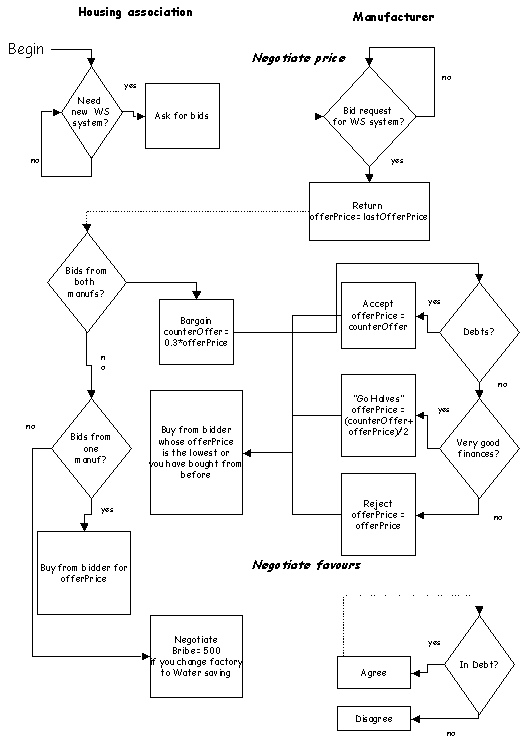
Figure 38. Bargaining Algorithm- price negotiation

b) Decision algorithm: Water Utility decision on priority action per turn ("ChooseAct" Appendix A)

Figure 39. Decision Algorithm: Water Utility

11.6.8 Description of Model Dynamics

An example (based on results from ZWG2): The water utility reacts to over supply by taking the opportunity to close a reservoir. The housing associations indicate the desire to reduce their water bills by encouraging the politician to advertise to encourage increased water saving behaviour amongst householders. This policy fails and the housing associations look towards technology in the form of water saving water systems for their households. This demand initiates a competitive response amongst the manufacturers who both change production in half their factories over to making water saving systems. The competition for both normal and water saving systems is so fierce that prices are rapidly driven ever lower, leading to healthy profits for the housing associations and one of the manufacturers, whilst the second manufacturer is reduced to subsidence.

As demand sinks due to the installation of the water saving systems, pressure is reduced on the water utility in that it can now afford to shut a further reservoir when it gets into financial difficulties due to the need to repair two reservoirs at the same time as revenues are falling from water bills. However, for the waste water utility, the fall in demand puts double pressure on them in that the higher concentration of wastes in the water outtake pipes makes it harder to maintain the lake water quality with basic purification methods. Crisis point is reached when the incoming money from bills is not enough to cover even the basic level of waste water purification methods. The two water utilities combine to encourage the politician to increase water prices in order to maintain basic services. The politician, realising that an election is due, dares not raise prices and happily realises that a buoyant private sector created as a result of the demand for water saving systems raises enough taxes for a temporarily high level of government subsidies. After a successful re-election, however, the politician raises the water price to make a further improvement to the system.

11.6.9 Implementation Language

ZWG1:

language: Java 1.3.1- b24

Environment: JBuilder 6

Platform: PC

Libraries: Quicksilver

Source code available: (available on request)

Documentation: see file ModelDocs.zip (available on request)

Developers: EAWAG

ZWG2:

language: paper and pencil

Environment: meeting room

Platform: table

Source code available: (available on request)

Documentation: see file WasserSpielVersion2.doc (available on request)

Developers: EAWAG

ZWG3:

language: PHP, HTML< Javascript

Environment: Server: APACHE, POstgreSQL. Client: Internet explorer 6 or Netscape 6

Platform: Server: Any Unix. Client: Any.

Source code available: http://www.soc.surrey.ac.uk/zwg3/source.php

Documentation: see bibliography

Developers: University of Surrey

11.6.10 Instructions for Running ZWG3 Code

The files provided should be copied to a directory on a host running the Apache (www.apache.org) web server. The directory must be within the document tree served by the the host. The server should also be running PHP (www.php.net) and PostgreSQL (www.postgres.org).

To run the game, PHP must have the configuration parameter 'register_globals' in the configuration file php.ini set to 'On'. This was the default setting until version 4.2, but more recent versions have the parameter set to 'Off', and so this must be changed before starting the game.

One must first create a Postgresql database. To do this, point a web browser to the ZWG3 page 'createdb.php'. This page is web form that requests the database administrator's username and password. Complete these fields and click on 'Go'. The database will be created.

The program can then be used, by pointing a browser at 'index.html' in the program directory. Players will need to be told that the password to enter the game is 'firma'.

Alternatively, the game can be run from the project's web site; see http://firma.cfpm.org/games.html

11.7 Conclusions

11.7.1 Example Simulation Output

ZWG1:

Figure 40 shows the results of a Monte Carlo simulation of 3 different scenarios which look at the sensitivity of three system indicators given different levels of environmental awareness in the population (an awareness that can be manipulated by policy makers through advertising campaigns). Each scenario lasts 20 simulation years and is repeated 110 times to produce the cumulative probability curves. These results show that, as expected, increasing the environmental awareness of the population leads to decreased drinking water demand as consumers attempt to save water. For example, the water demand graph shows that when environmental awareness is 5 then there is a 0.95 probability that the scenario will end in water demand being at least 50 units. When it rises to 10, the probability that it will be higher than 50 is only 0.45 and for values higher than 60, there is no probability at all.

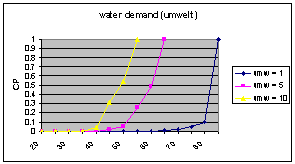
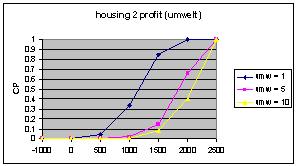
Figure 40. The cumulative probabilities (CP) of values for three system indicators at the end of a 20 year simulation: the drinking water demand; the water utility profits and housing association profits (averaged over the final five years of the simulation).

Water utility profits rely on maintaining a balance between supply and demand and a high amount of demand, since reservoirs cost money to be maintained and the only income is from water consumption. The water utility profits graph thus shows a non-linear relationship between environmental awareness and profits. As environmental awareness rises from 5 to 10, the probability of profits being lower than -2500 rises from 0.05 to 0.3. This shows the impact of the loss of income from water demand. However, when the environmental awareness falls to 1, the water demand is so high that extra reservoirs need to be built to maintain the water supply/demand ratio above 1. Hence increased costs of maintenance and construction outweigh increases in consumption income.

Whilst the likelihood of high water utility profits decreases with an increase in awareness from 5 to 10, the probability of higher profits for the housing associations increases. Purchases of water saving technology by housing associations seeking to save costs, allied to an awareness-induced decrease in water consumption by their tenants, lead to lower water bills.

ZWG2:

One example of output (in addition to Section 1.2.8, above) is the change in prices of water systems during the game session used to generate a bargaining algorithm (Table 2).

Round	Hersteller1		hersteller2		Accepted L 1		Accepted L2
	Norm	WS max 1	Norm	WS (max 1 to sell)	Norm	WS	Norm	WS
2	150 (L2)	500(300 ) 300 (L2)	250 (L2)	400(300) 300 (L1)		300	250/150	300
3	400 for both	400 for both (L1)	250 (L1)	300 (L2) 300 (L1)	400 for both			300
4		250 (L2)	400 for both (L1)	300 (L2) (200) 250	400 for both			250
5	150 (L1)	200 (L1) (180)	150 (L1)	250 (L1) (180) 180		180
6		200 (L2)		250 (L2)				200

Table 7. Prices of Water sanitation systems during a ZWG2 game. Bold means a sale was agreed: price in brackets is a counter bid by a housing association - therefore "400 (300) 300 (L1)" means that the initial bid was 400, followed by a counter bid from housing association L1 of 300 which was agreed by the manufacturer and L1 bought at this price.

ZWG3:

ZWG3 is a strategy game, where the output is displayed to players interactively on the web browsers. It is therefore hard to get a sense of the output in the same way as a normal simulation. However, all actions within the program, both those made by computational agents and those by human players, are logged and Figure 41 shows an excerpt from a typical log file.

Figure 41. Output Protocol from ZWG3

11.7.2 Results claimed as significant

The results of the use of the models is mainly in terms of how the stakeholders' discussion have developed with their use. The main finding is that the stakeholders have moved away from water saving-based management solutions to looking at how security and efficiency of supply can be first managed.

In terms of social learning, the gaming has generated discussions on the possible undesired consequences of water saving in the city without control of water demand and reduction of supply infrastructure. It has shown how the aggressive marketing of water saving systems in a market willing to buy them, can have serious consequences for the water utilities, e.g. over capacity problems, poor finances, threatened water quality. There have also been debates on the institutional inadequacy of splitting the water supply and waste water utilities, and the possible sources of funding for subsidies for these utilities.

As noted above, during the gaming sessions there were debates about possible funding sources for utility subsidies which would help assuage the high level of utility debts caused by environmentally aware water saving and a consequent fall in demand. Given the scenarios developed in ZWG1, it becomes clear that one source may be the housing associations. A tax could be included in the price of the water saving systems they buy or in the price of their water.

In addition, the feedback from ZWG2 has been used to improve the agent-models in the ZWG1 and ZWG3. Of particular use has been the elicitation of a bargaining model that describes how manufacturers and housing associations bargain a price for water systems (see

Figure 38). In addition, the motivational rules determining agent decision making have also been elicited.

11.7.3 Methodological Lessons

The major methodological lesson comes from the interaction of the three implementations in that ZWG1 can be used to calibrate ZWG2 which can then be used to build up user confidence in and provide cognitive models for ZWG1 in return. Individually, there has been the realisation that role playing models must be tailored to particular uses and that the translation of a board game to an internet version (ZWG2->ZWG3) is non -trivial.

11.7.4 Future Development

ZWG3 is still being developed and tested for use with stakeholders and members of the public in a participatory setting.

11.7.5 Published works relevant to the model

Participatory Modelling Process (ZWG*, ZWG1)

Hare, M.P., & C. Pahl-Wostl. in press. Stakeholder categorisation in processes of participatory integrated assessment. Integrated Assessment.

Hare, M.P., D. Medugno, J. Heeb & C. Pahl-Wostl (2002) An applied methodology for participatory model building of agent-based models for urban water management. In (Urban, C) 3rd Workshop on Agent-Based Simulation. SCS Europe Bvba, Ghent. pp 61-66

Role playing (ZWG 2, 3)

Asakawa, T., Gilbert, N. in press. Synthesizing Experiences: Lessons to be Learned from Internet-mediated Simulation Games. Simulation & Gaming An Interdisciplinary Journal of Theory Practice and Research.

Gilbert, N., S. Maltby and T. Asakawa. (2002) Participatory simulations for developing scenarios in environmental resource management. In (Urban, C) 3rd Workshop on Agent-Based Simulation. SCS Europe Bvba, Ghent. pp 67-72

Hare, M.P., N. Gilbert, D. Medugno, T. Asakawa, J. Heeb & C. Pahl-Wostl. (2001) The development of an internet forum for long-term participatory group learning about problems and solutions to sustainable urban water supply management. In Hilty, L.M. & Gilgen, P.W. (Eds) Sustainability in the Information Society, 15th International Symposium Informatics for Environmental Protection, Part 2. Metropolis Verlag, Marburg. pp743-750. ISBN: 3-89518-370-9.

Hare, M.P.,J. Heeb & C. Pahl-Wostl (2002) The Symbiotic Relationship between Role Playing Games and Model Development: A case study in participatory model building and social learning for sustainable urban water management. Proceedings of ISEE, 2002, Sousse, Tunisia

Hare, M.P., N. Gilbert, S. Maltby & C. Pahl-Wostl (2002) An Internet-based Role Playing Game for Developing Stakeholders' Strategies for Sustainable Urban Water Management : Experiences and Comparisons with Face-to-Face Gaming. Proceedings of ISEE 2002, Sousse, Tunisia

11.8 Appendix A: Object model and interaction diagram

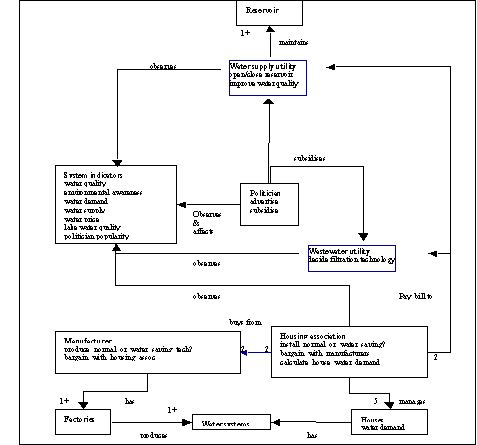
Figure 42. The Object Model of ZWG*

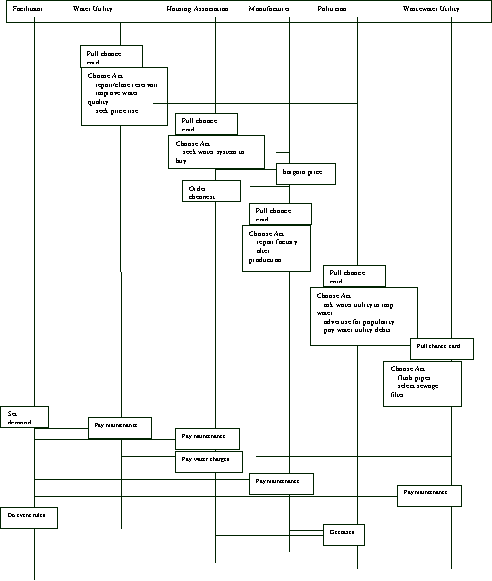
Figure 43. The Interaction Diagram of ZWG*

12 A model of water demand and social imitation

Olivier Barthelemy, Bruce Edmonds and Scott Moss, Centre for Policy Modelling

12.1 Modelling Context

12.1.1 Description Domain Context

Water demand management necessities have pushed the institutions as well as the companies to try to predict the consumption of drinking water for households in the near future. The timescale of structural decisions is such that no existing tool was able to inform such decisions that had no well-known flaws. Therefore this model is using a Multi Agent System approach. It allows a dynamical evolution of the system structures as well as the agents.

12.1.2 Original Purpose of Model

This model is devised to be used by stakeholders in different situations: Typically, the water companies should infer from the simulated behaviour some possible future patterns of water consumption in the presence of climate change. Also, because of the explicit processes represented in it, it is a very good starting point for a common language and/or reflection and hence will facilitate the participative process.

12.1.3 How was the Model Actually Used

Presented to stakeholders, the model was commented on and modified in accordance with their remarks. It will be used as the basis of a role playing session with the participation of the environment agency, water companies, and customers. The actual building process for the model raised previously unasked questions and led to a different kind of reflection from the participating stakeholders.

12.1.4 Relationship to other Models

The first version of this model was developed by Scott Moss, and will be published in a forthcoming volume of Integrated Assessment. The now revised version uses some of the original modules, but has more possibilities, including for example some different adoption processes.

It retains from the initial model the ground and policy behaviours, the grid positioning, the process of communicating, as well as the endorsing method. The modifications were added to the imitation process (more precisely in the selection of the actions to imitate), the possible variations of main influences for households (how important is the influence of the different components of their environment), and to the innovation emergence (implementation of a more realistic breakdown and replacement process), as well as to the available appliances and their properties.

12.1.5 Relationship to FIRMA’s Aims

This model has resulted from fairly close cooperation and consultation with a variety of water companies in the UK. It reflects some of their concerns with demand management, especially in times of drought. It is an application of agent-based modelling which concentrates on the social issue of imitation and suggestion as it interacts with domestic water demand. It is planned that it may form part of a participatory exercise with representatives of water companies to be run by SEI/ECI at Oxford.

12.2 Model Design

12.2.1 Intended interpretation

The model results must be viewed cautiously, they are aimed at representing the complex behaviour of real life agents, and are not absolute numbers because the model is descriptive, in the sense that all its components are explicit relations, designed to make it easy for stakeholders to understand. The agent base leads to an easy identification from stakeholders to some of the software agents in the model. Because of the analogy it is straightforward to identify the role, environment and actions or reactions of each agent.

12.2.2 Original Sources for Model Design

The initial model has been created from basic rules of behaviour and stakeholders’ suggestions. Although it is still mainly based on this first representation, it has evolved according to the remarks made in meetings and additional information about the behaviour of agents involved.

The endorsements idea and implementation takes its sources in sociology (Brown ??? for the particular liaison between most identical agents, Cohen ???? for the endorsements). The ground has been modelled using geographical references and algorithms.

12.2.3 Static Structure

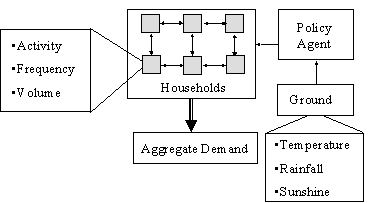
Figure 44. Structure of the model

The structure of the model is represented in the diagram above. The small arrows represent the interactions, the ground, the policy agent and the households are the main agents, and their different properties are expressed as activity, frequency and volume, or temperature, rainfall and sunshine.

The temperature, rainfall and sunshine are used to compute the evapotranspiration, and the resulting soil moisture. This moisture is hence the output of the ground part. It is taken as an input from the Policy agent. It is being analysed, and if it is below a specified threshold, the policy agent broadcasts some messages to reduce water use. These messages consist of a specific (reduced) volume and frequency of use for particular appliances. The households, defined by their set of appliances, volume per use, and frequency of use, might then react to these recommendations.

12.2.4 Temporal Structure

The model can be considered as having several interacting groups of components. The ground components, the policy agent part, and the household part. The ground dynamically computes the soil moisture. The Policy agent reacts to this moisture if it falls below a predefined value. If this happens, it broadcasts a signal for households to reduce their use of water.

12.2.5 Important Parameters

The most important parameters in the model are the following:

• the proportion of households in each category (self centred, local centred, global centred), as it influences the sensitivity of the reaction of the households to their neighbours and their environment.
• the temperature and rainfall, triggering or not the Policy Agent actions
• the density of households on the grid, and the range limiting possible interactions.

12.2.6 Initialisation

The initialisation of the model requires some user input (user), and has default values or objects / rules generation (sdml). They are as follow.

1. (sdml) create and activate sub agent Thames World

2. (sdml) create and activate sub agents Thames Ground and Firma Model

3. (sdml) create the time levels (year, month)

4. (user) define the maximum AET (default: )

5. (user) define the mean latitude of the area (default: 51)

6. (user) specify the temperature and data file

7. (sdml) initialise time level

8. (user) specify time level boundaries (default: 12 months in a year)

9. (sdml) kc table

10. (user) specify precipitation data filename

11. (user) define maximum soil water

12. (user) define initial year

13. (user) define final year

14. (user) define maximum runoff

15. (user) specify file containing name of appliances, and format

16. (sdml) create environmental aspects

17. (user) define weights for GS, NS, SS

18. (sdml) time level activation

19. (user) define grid size(default: 16*16)

20. (user) define number of cells agents can see (default: 4)

21. (user) specify eventual introduction of new appliances, date, and replaced appliance

22. (user) specify private activities

23. (user) define rate of decay of remembered endorsements (default: 2.5)

24. (user) define the population size (default: 100)

25. (user) specify Weibull parameters for replaceable appliances

26. (sdml) generation of population

27. (sdml) generation of meta agents

This takes the user to the stage where all the variables are initialised, and the agents are created and activated, and ready to “behave”.

12.2.7 Key Algorithms

The modified Thornthwaite algorithm is used to compute the soil moisture through potential evapo transpiration (PET) from temperature and hours of daylight per day (as in Food and Agriculture Organisation 1986).

The value of the unadjusted PET at temperatures above freezing is calculated as:

PET	Temperature (T) range
- 415,8547 + 32.2441T – 0.4325T2	26.5 ≤ T
16.5 (9 T / H) a	0 ≤ T < 26.5
0	T < 0

where H is heat defined as

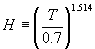
and the exponent a is

a ≡ 6.75e-7 H 3 - 7.71e-5 H 2 + 0.01792 H + 0.49239

The day lengths are calculated from the day relative to the winter solstice and the latitude. The monthly PET values are adjusted to reflect the difference in water use between a grass surface and a mixed landscape of grass, trees and shrubs. The monthly correction factors are:

Nov – Dec - Jan – Feb - March	April	May	June – July - Aug	Sept	Oct
0.8	0.9	1	1.1	1.05	0.85

The model also calculates the runoff of water but this value was not used here.

Another important algorithm is used to compute and compare endorsements. Cohen’s original endorsements approach allocated endorsement tokens to classes of importance. The action chosen would be that which had the most endorsements of the highest class or, if several had the same number in the highest class, the action that was tied in the highest class but had the most endorsements in the second highest class. If there was another tie at the second highest class of endorsements, the third or if necessary the fourth or lower class would be used to break the tie.

A more general approach, and that used here, is to define a number base, b, and evaluate each endorsed object according to the formula

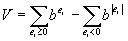
where e_i is a (usually integer) value associated with the i^th endorsement token. Negative values of endorsement tokens indicate naturally enough that they are undesirable. The higher the value associated with an endorsement token, the higher the class of tokens containing that particular token. The value of b is the importance of an endorsement token relative to the value of a token in the class below. If the base is 2, then an endorsement of class three contributes 8 to the endorsement value of an object while an endorsement of class two contributes only 4. For values of b larger than the number of tokens in any class used to endorse any object, the results from this evaluation scheme are the same as from Cohen’s evaluation scheme. For smaller values of b it is possible for a large number of lesser endorsements to outweigh a small number of endorsements of greater value.

12.2.8 Description of Model Dynamics

Every agent will start with some endorsements on its environment (including its own appliances). They are personal and unique for a given time step. The system will also make a list of the different appliances available to the agent, depending on its previous ownership and the time.

For this set of available actions , the endorsement value is computed, and the household agent makes the decision of adopting or not (whether it is a change of ownership or frequency, or volume) depending on that value.

Here is an example of the history of one action from one agent’s point of view:

Month 1	used, endorsed as self sourced
Month 2	endorsed as recent (from personal use) and neighbour sourced (used by agent 27) and self sourced (remembered)
Month 3	endorsed as recent (from personal use) and neighbour sourced (agent 27 in month 2).
Month 4	endorsed as neighbour sourced twice, used by agents 26 and 27 in month 3, also recent
Month 5	endorsed as neighbour sourced (agent 26 in month 4), also recent
Month 6	endorsed as neighbour sourced (agent 26 in month 5
Month 7	replaced by action 8472 (appeared in month 5 as neighbour sourced, now endorsed 4 times, including by the most alike neighbour – agent 50)

12.2.9 Implementation details necessary to get the simulation to run but not considered important for the results

The actions are evaluated according to their endorsements. The possible endorsements are, for example: that the action was used by neighbour, that the action was used by myself, that the action was recommended by the policy agent, or that the action was used by the most alike neighbour.

They are also dependent on the available appliances. Each household starts with a given set of appliances. This will not change, apart from those that are specified as replaceable. For these, a household will collect all their endorsements, and transform them into a single aggregate value. The higher the value, the most favoured the appliance. So for each appliance, the household’s behaviour will change, as a combination of the observations. A priority is given to the newest appliance if two interchangeable appliances have the same endorsement value.

12.2.10 Source Code

The model is implemented in SDML. The language itself is freely available from the Centre for Policy Modelling website. The necessary modules for the simulation are available on request.

12.3 Conclusions

12.3.1 Example Simulation Output

Here is a sample of the output from the model. It shows the evolution of water consumption with respect to time, for some specific parameter.

Figure 45. The aggregate water demand resulting from a single run of the model

Some more details about the model’s output can be obtained on request from the CPM.

12.3.2 Results claimed as significant

One of the significant results is the observations one can make about the imitation patterns and their sensitivity to their own characteristics, and the climatic events for example.

12.3.3 Methodological Lessons

Some lessons must be learnt for the participatory component of the model. The interaction is useful for building the model, but it did not happen as much as expected at the start of the research. The methodology is so different from what is already existing that most of the participants in the meetings had to be explained the difficulties and the potential of the approach.

12.3.4 Future Development

The model can be extended in various ways. Firstly, it is intended to refine the adoption process of innovation, as well as a different type of decision process from the households. It is also possible to generate multiple policy agents with different objectives and behaviours, for example environmental

12.3.5 Published works relevant to the model

Olivier Barthelemy, Scott Moss, Thomas Downing and Juliette Rouchier (2001) Policy Modelling with ABSS: The Case of Water Demand Management. CPM Report No. 02-92. http://cfpm.org/cpmrep92.html

Brown, R. (1965) Social Psychology, New York: The Free Press.

Cohen, P. R. (1985) Heuristic Reasoning: an artificial intelligence approach. Boston: Pitman.

Moss, S. (in press) Agent Based Modelling for Integrated Assessment. Integrated Assessment.

13 Bilateral versus multilateral negotiation

Scott Moss, Centre for Policy Modelling

13.1 Modelling Context

13.1.1 Description Domain Context

It is not hard to find examples of failed negotiations. At the same time, there are clearly many examples of successful negotiation that form part of the small change of everyday life. Difficult negotiations involve both more parties and larger numbers of related issues than do the examples of regularly successful negotiations. But there is a second difference, as well. The examples of success are negotiations among two parties and if the parties are in fact composed of several individuals, within each party there are no differences of goals. Whereas the large scale negotiations generally have to reconcile a wide range of interests.

13.1.2 Original Purpose of Model

The purpose of the model was to develop techniques for modelling multi lateral negotiation. In particular, it was to be the first prototype for a description of stakeholder negotiation in the Limberg basin of the River Meuse.

13.1.3 How was the Model Actually Used

It was used to analyse the reasons why successful multilateral negotiation is so difficult to achieve.

13.1.4 Relationship to other Models

This is a first-generation model that informed the development of a second model that is intended to model in an abstract context the actual negotiation processes among stakeholders in the Limberg basin.

13.1.5 Relationship to the AIMS of FIRMA

Understanding the nature of negotiation is difficult, and yet it transpires that it is crucial to many water management issues and problems. This model is an investigation into this nature and informed the development of the core negotiation model.

13.2 Model Design

13.2.1 Intended interpretation

This is an investigation into the difficulties and limits of modelling multilateral negotiation. Although it is an abstract model, it is intended to provide a canonical model of negotiation with mappings to and from the negotiation setting and practices relevant to the Limberg Basin. Within the model there is a class of negotiating agents representing negotiators. Both the state of the environment and the negotiating positions of the agents are represented by digit strings. Because the digits at each position of the digit string can take any of an arbitrary number of integer values, the fineness of the grain of the various negotiating positions can be captured with arbitrary precision.

13.2.2 Original Sources for Model Design

The main design ideas are drawn from earlier models by Moss – including his models of household demand for water in the Thames Valley. Originally, the main design features come from social psychology and from approaches to conflict resolution in expert systems. Also, this was intended to serve as a basis for a canonical model of negotiation in the sense of (Moss, 2000).

13.2.3 Static Structure

There are a fixed number of agents which are attempting to haggle over the values of a fixed number of issue. They choose negotiation partners and attempt to reach an acceptable agreement on all issues. If this occurs they form a coalition which can then attempt to haggle with other agents or coalitions. Thus this is a model of multi-dimensional haggling. The model contrasts the position with only two agents – where agreement is possible and that with more than two where agreement (using the process described) is not possible.

13.2.3.1 Abstract representation of agents’ positions

The negotiating stance of each agent is represented by two digit strings. One string – the agent’s position string – represents the preferred outcome of the negotiating process with respect to each issue under discussion. The other string – the agent’s importance string – represents the importance the agent attaches to achieving its preferred outcome for each issue. For example, and agent’s desired outcomes might be represented by the position string

[2 1 4 2 3 0 0 3 2 4 1 0 2 1]

where the value at each index of the string is a representation of the desired outcome of the negotiating process for a particular issue. The issue corresponding to each index of the position string is the same for every agent. The number of integer values that can be assigned to any position is determined by the model operator at the start of each simulation run with the model. In this case, the values taken at each index of the position string are in the interval [0,4].

The corresponding importance string of the agent might be

[3 1 0 2 0 3 3 1 0 2 3 1 0 1]

indicating that the most important objectives of the agent (indicated by the 3s in the importance string) are to obtain a value of 2 for the issue denoted by the first digit of the strings and the value 0 for the sixth and seventh issues and the value 1 for the 11^th issue.

The effect of the negotiation process is necessarily represented as changes in the position strings of the participating agents. Moreover, although not implemented in the simulations reported below, it seems likely that the importance attached to different positions will also change over the course of the negotiation process – perhaps as it becomes important to maintain common positions important to partners which whom agreement has been reached.

13.2.4 Temporal Structure

13.2.4.1 Selection of negotiating partners

Agents could have any of a wide variety of strategies for the identification of issues about which to negotiate and for the selection of negotiating partners. At one extreme, an agent could identify an issue and then negotiate with every possible (or known) agent concerning that issue. At the other extreme, agents can select other agents with which to negotiate and determine the issues in collaboration with the selected agents. The strategy to be modelled – whether one of these extreme cases or some combination or set of parallel strategies – should depend on observation and the evidence of domain expertise.

In the model reported here, the negotiating strategy was driven by the selection of agents as negotiating partners. The criteria for selecting an agent with which to negotiate were based on trustworthiness, reliability, similarity, helpfulness, acquaintanceship, untrustworthiness, unreliability, unhelpfulness. One agent identifies another as reliable if the other agent responds affirmatively to a suggestion that the two agents negotiate. An agent will identify another as trustworthy if its public negotiating position reflects previous agreements between the two agents. An agent is helpful if it suggests to two or more other agents that they might usefully negotiate with one another and agreement among those agents is realised. An agent will identify another as similar if, among all of the negotiating positions known to the agent, the other agent shares the largest number of position values. One agent can know another either because of an approach at random or because the other agent has made contact by suggesting a negotiation.

Each agent in the model has rules for attaching endorsements – tokens reflecting the selection or aversion criteria – to other agents. The ranking of the importance of endorsements is, in the first instance, random except that opposite endorsements (helpful and unhelpful, trustworthy and untrustworthy, reliable and unreliable) have rankings of the same magnitude and opposite sign. So that if trustworthy is the most important positive endorsement, untrustworthy will be the most important negative endorsement. Each agent will have its own initial ranking of positive (and therefore negative) endorsements. Each agent will select the best endorsed agent it knows as a negotiating partner at each stage.

Over the course of a negotiation process, each agent will continue to learn about other agents – a process represented by the ongoing attachment of endorsements. Each agent will also learn which are the most important criteria to use in selecting negotiating partners. If the use of a particular set of rankings of criteria leads to the conclusion of an agreement with a selected agent or group of agents, there is no reason to change the relative importance of the different criteria. If no agreement is reached, then there will be less confidence in the current ranking – though it is unlikely that a wholesale change in rankings will follow from every failure to achieve some agreement.

In order to capture this learning process about endorsements and their relative values, agents’ learning is represented by the Chialvo-Bak (1999) algorithm described below.

There are two advantages to be gained from implementing this learning process. One is that the simulations determine the most important criteria to be used in choosing negotiating partners. The other is the flexibility of the ordering of criteria since it is possible that the importance of different criteria will change over the course of any negotiation process. It is possible, for example, that reliability is most important at early stages so that there is some meaningful communication but that trustworthiness is most important in the final stages.

13.2.5 Important Parameters

The most important parameter of the model is the number of negotiating agents. The results are not highly sensitive to other parameter values such as the number of issues (represented by the lengths of the digit strings) and the fineness of the grain of the negotiating positions

13.2.6 Initialisation

The number of agents and the length of the digit string representing the state of the environment are set by the model operator. The number of positions in which each agent has an interest and the relative importance of that interest to the agent are the realisations of a uniform random number within bounds set by the model operator. The parameters have no default values.

13.2.7 Key Algorithms

The main novelty in this context is the use of the Chialvo-Bak (ref) algorithm to represent agent learning. This algorithm uses a sort of neural network approach but without positive reinforcement of synapse weights. In the present case, the input neurons are attached to endorsement tokens and the output neurons are ranking values to be attached to the endorsements. There were five intermediate layers, each containing 40 neurons. Starting with the input neurons, each neuron as seven synapses out to the next layer until the output neuron layer is reached. The paths followed from input to output neurons is determined by the synapse with the highest weight emanating from each neuron. When agreement is not reached, the value of each synapse on the dominant path is reduced by a small amount (usually by one per cent) and the sum of the reductions is distributed equally among the rest of the (2000+) synapses. Consequently, changes in the behaviour of an agent take place relatively infrequently but will, from time to time, be fairly extensive.

13.2.8 Description of Model Dynamics

The dynamics of the model are driven by the agents’ negotiating strategies. It is a commonplace in the negotiation literature that the least important issues should be addressed first. Once negotiating styles have accommodated one another and a recognition of reliability and trustworthiness established, there is a basis for considering more important substantive issues. The most difficult issues are left to the last.

Every agent in the model reported here adopts this sort of strategy. Each agent offers to its preferred negotiating partner a list of positions for the issues the agent found least important among all of the issues that had not yet been resolved. Denote the first agent as A and A’s preferred negotiating partner as P. IfP made some offer of negotiating positions then, if that offer contained values for positions that A found least important, and also some values that A found to be more important, then A would accept P’s offer on the least important issues in exchange for P’s acceptance of the same number of A’s positions. In general terms, some agreement could always be reached provided the two agents preferred to negotiate with one another and each was able to offer to change one or more of its least important positions in exchange for the other agent agreeing one of its more important positions.

Once any pair or larger group of agents fully agrees on all positions, they form a coalition to negotiate with agents not in the coalition or with other coalitions. The process ends when all agents are members of a single coalition or super-coalition (i.e. coalition of coalitions of coalitions …). In practice, the only simulated negotiation processes that reached a conclusion were all of the two-agent processes.

13.2.9 Implementation details necessary to get the simulation to run but not considered important for the results

The number or range of the strings representing the issues did not seem to affect the outcomes. Nor did the precise initialisation or size of the neural network. Although the Chialvo-Bak algorithm is attractive in that it provides an accessible and credible learning story it is hypothesised that the exact learning algorithm concerning the choice of negotiation partner is not critical to the results. It is more likely that the bargaining strategy may be improved, by being made more “intelligent” but it is thought that unless mechanisms for intelligent coalition formation are not included that the precise strategy is also not critical to the results.

13.2.10 Implementation Language

SDML 4.1

13.2.11 Source Code

Source code will be available from the website.

13.3 Conclusions

13.3.1 Example Simulation Output

The progress of bilateral negotiation was represented by changes in the differences of negotiating positions of two agents. These differences were measured as the Euclidian distance between the two position strings interpreted as coordinate vectors in a 30-dimensional hyperspace. An example of the progress represented by this measure is given in Figure46. This progress is typical of all runs with two negotiating agents. The range of the number of cycles elapsed before agreement was reached was from 8 to 12 with the bulk of the distance eliminated in the last half or less of the cycles. There was no learning for the agents to do since they had no choice of negotiating partners.

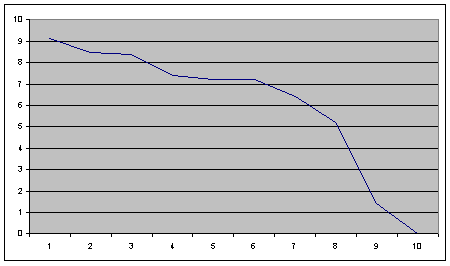
Figure 46. Distance between 2 agents in bilateral negotiation

Although simple negotiating strategies work well for the modelled bilateral negotiation, they do not work at all in simulations of multi lateral negotiation with three or more agents. Simply trading agreements on more important positions in exchange for giving up less important positions is evidently insufficient. The problem here is that moving towards agreement with any other agent typically involves increasing the distance to some other agent. It is no doubt possible to devise a variety of arrangements under which agents combine in pairs to reach agreement and form a coalition and then pairs of coalitions negotiate to form a super-coalition and so on until every agent is in the coalition. The value of such an exercise is not clear. Certainly there is no evidence that such a tree of bilateral agreements is a realistic description of successful negotiations, though equally certainly there is some element of small groups coming together on particular issues.

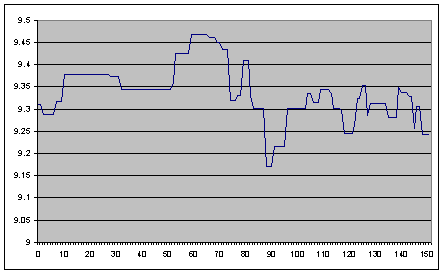
Figure 47. Average distance between negotiating positions of agents in nine-agent simulation

13.3.2 Results claimed as significant

That multilateral negotiation is fundamentally different from bilateral negotiation. Lessons obtained from modelling bilateral negotiation do not naturally or necessarily inform the modelling of multilateral negotiation beyond two parties.

13.3.3 Methodological Lessons

If good science starts from good observation, then the implications of these simulation results are that we should model actual, individual processes of multilateral negotiation. The modelling itself will doubtless yield insights into the elements of successful and unsuccessful negotiation processes and the modelling of a range of such processes is likely to inform the development of modelling techniques that apply quite generally to descriptive simulation models.

13.3.4 Future Development

The second phase of this modelling development has been to implement a model in which agents negotiate within an environment characterised by self organised criticality created in part by random events and in part by the nature of human behaviour as represented in the model. Self organised criticality generates clusters of volatile events characteristic of floods, earthquakes, volcanic activity and a variety of social phenomena of a sort that is relevant to both flood control issues and the effects of human intervention on those activities. The abstractions of negotiating positions and environmental states are unchanged in the further version.

The third phase specifically incorporates negotiating procedures and strategies as described by ICIS – our partners developing the Limberg Basis application.

13.3.5 Published works relevant to the model

Scott Moss (2002), “Challenges in Agent Based Social Simulation of Multilateral Negotiation”, chapter 31 in Dautenhahn, et al (eds.), Socially Intelligent Agents: Creating Relationships with Computers and Roots (Kluwer Academic Publishers).

Chialvo, D. R. and P. Bak (1999). "Learning from Mistakes." Neuroscience 90(4): 1137-1148.

Moss, S. (2000). "Canonical Tasks, Environments and Models for Social Simulation." Computational and Mathematical Organization Theory 6(3): 249-275.

14 Neg-o-Net Version 1.0 model

David Hales, Centre for Policy Modelling

The Neg-o-Net model is a generic agent-based computational simulation model for capturing multi-agency negotiations concerning resource and environmental management decisions. The model is intended to be generic enough to be applicable to many regional applications with minimal re-programming. Neg-o-Net was developed by the Centre for Policy Modelling at Manchester Metropolitan University. The initial design was produced in collaboration with IP-CNR Rome partners.

14.1 Modelling Context

14.1.1 Description Domain Context

The model is a generic framework for simulating various multi-agency negotiation processes centred on resource and environmental management. Stakeholder “viewpoints” are represented as networks of states of the world and actions that are believed to move between those states. Each stakeholder (agent) has different (possibly conflicting) viewpoints and goals. Negotiation processes can be applied at three distinct levels – action trading (a kind of barter), belief exchange and goal exchange. In the current version (1) three simple negotiation protocols have been implemented along with example viewpoints – for illustrative purposes.

14.1.2 Original Purpose of Model

The purpose of constructing the model was to solidify some of the on-going theoretical discussions at previous FIRMA workshop meetings in Clermont-Ferrand, Oxford and Maastricht concerning the possibility of a “generic negotiation model” that could be tailored with minimal programming effort to specific partner areas. Consequently, the current model separates the agent “viewpoints” from the code by providing a simple “viewpoint description language” allowing for agent viewpoints to be described in a high-level and intuitive way.

The main purpose of version 1 was to demonstrate that such a generic model was possible and could be used by the FIRMA partners in collaboration with the Centre for Policy Modelling (CPM) for application to specific regional variations. This aim was achieved, and the CPM is currently working with the Maastricht group to tailor the model to that region’s requirements. Specifically, to implement (at the viewpoint level of detail) the negotiation processes studied in detail by the Maastricht team involves government, citizen groups and gravel extractors. The Maastricht team have already produced a simulation model at the level of preferences to describe the process. A properly extended Neg-o-Net should allow for the explicit representation of the beliefs of agents and the dynamic negotiation process. This would allow the preferences to be “unpacked” into the underlying beliefs. For example, agents will be able to give reasons for disagreeing with proposed government plans and the government agent will attempt to reformulate plans to take account of this. These processes will be given as a natural-like language trace that should be understandable to anyone familiar with the domain.

Additionally, the model is to be integrated into the online Zurich Water Game (Gilbert et al 2001). Here, the agents will interact with people playing the game. Currently, the artificial agents in the game have fixed viewpoints, strategies and negotiation protocols but utilising the flexibility of the Neg-o-Net model should allow for these to be easily changed. This could offer future potential for knowledge elicitation – by allowing real stakeholders to negotiate with artificial agents and comment on their deficiencies as a realistic representation.

14.1.3 How was the Model Actually Used

The model has currently been used for demonstration purposes to the regional applications teams. Currently the CPM is working intensively with the Maastricht team to specialise the next version of Neg-o-Net to the negotiation processes identified in that region.

14.1.4 How the model relates to FIRMA’s aims and objectives

The model allows the explicit representation of a negotiation between parties with given their different views as to what is possible in the world with respect to the relevant domain. It is specifically designed to facilitate its integration into models which combine other relevant aspects of the situation in each of the five regions. It is also designed with a view to the participatory elicitation of representations of the parties different views in terms of simple diagrams. Thus it forms a key part of analysing those hydrosocial issues of water management that include negotiated elements. It is the key core element that will enable the development of a somewhat generic model design, but one which is deeply relevant to the regions separate problems. Finally it is designed to facilitate the participatory integrated assessment in the five regions.

14.1.5 Relationship to other Models

The Neg-o-Net model was inspired by the Part-Net model (Conte & Pedone 1998) which in-turn was an extension of the Dep-Net model (Conte & Sichman 1995). Part-Net and Dep-Net were produced by the IP-CNR Rome modelling group and the SimCog group São Paulo. Neg-o-net was designed in consultation with the Rome group and is consistent with their developments in the area of social norm dynamics. A subset of goal level negotiation may be viewed as the spread of normative beliefs. This could be seen as the “top-level” stopping condition in the three levels of negotiation previously outlined. Specifically, if an agent wishes to convince another to adopt a high-level goal (for example “increase the quality of life of the citizens”) for which it has no justifying higher-level goal then these may be considered as a form of institutional norm. In this context, theories of norm adoption would be applicable and capable of being integrated into the Neg-o-Net model should this be required (Pedone 2000).

Additionally Neg-o-Net leaves space for the integration of an environmental model (which would be produced by the regional application teams). In order to drive a simulated negotiation run (where actions are taken with environmental consequences and the results observed and reacted to) an environmental model is required. Future work may integrate the already developed Maastricht environmental model into the Neg-o-Net framework. At the end of a negotiation process agents submit the agreed actions to the environmental model, which then returns the environmental consequences of those actions.

14.2 Model Design

14.2.1 Intended interpretation

The model is descriptive. This means the interpretation is that of a dynamic description of the kinds of negotiation process that occur for given regional applications. The current non-specialised demonstration versions (1) gives an example of the kind of negotiation process descriptions that can be captured – but is not linked to any specific regional application. In this sense (as stated previously) version 1 of the model is a demonstrator and is currently being applied to regional applications.

The target phenomena are that of a multi-agency (stakeholder) negotiation dialogue and subsequent plans of action. Agents communicate in natural-like language their requests, proposals and suggestions, come to agreements and then take action. Each of these should correspond directly to real world stakeholder consultations and action plans at the descriptive level. Each agent has a viewpoint representing beliefs, goals and possible actions. These viewpoints should coincide with real stakeholder viewpoints at the given level of detail.

The aim of the model is not to be predictive in any narrow sense. We aim to produce traces of plausible and possible negotiation dialogues and action plans. The validation of the plausibility of the output should ultimately be directly from stakeholders with minimal mediation provided by modellers.

A well validated Neg-o-Net model applied to a regional application would offer some kinds of wider predictive utility. It may be possible to show that for given environmental assumptions, viewpoints and negotiation protocols, certain kinds of plan are never possible or unlikely. It might also be possible to show that certain disagreements are inevitable or likely. Given this, the ultimate aim of such modelling would be to computationally evaluate new negotiation protocols computationally and select or propose those which appear to increase the likelihood of desirable outcomes (policy advice) – though this is still a distant aim at present and beyond the scope of the current project.

14.2.2 Original Sources for Model Design

The general approach was inspired by the previous models Dep-Net (Conte & Sichman 1995) and Part-Net (Conte & Pedone 1998), although the emphasis is different from those models. The initial design process was carried out intensively with the IP-CNR Rome group. The Part-Net framework was extended to incorporate a three layered negotiation process and a digraph causal action/state viewpoint belief representation. In this scheme each agent stores their own viewpoint digraph based on their beliefs about states and actions. Arcs represent transitions between states (nodes). Each arc is labelled with some set of “actions” which are believed to produce movement between each node. Each node stores a world state description (including some set of environmental indicators) and some set of possible actions available to the agent holding the given viewpoint. Nodes are ordered by agents based on some desirability function – some weighted sum over state indicator values attached to each node.

14.2.3 Static Structure

In the current version (1) of the model the viewpoint digraphs stored by each agent do not change (in later versions, when belief and goal exchange is implemented, these structures will become dynamic). Figure 48 shows three example (essentially trivial and non-realistic) viewpoint digraphs. These represent the viewpoints of three agents (a manufacturing company, a political party and a citizens interest group).

Figure 48. Some illustrative viewpoints (simplified fragments) for three agents. Note that each node contains a label, indicator values and a list of possible actions. Arcs are labelled with (believed) required action(s) to make transition to new state

In Figure 48, each agent has a viewpoint with only three nodes – this is a simplified example. The first text line listed at the top of each node is simply a label to identify the node – it should sum-up the world state concisely. The next line of text gives the values of indicators that the given world state represents. Each remaining line lists a possible action that the agent holding the given viewpoint believes it can take. Each arc is labeled with any actions (believed to be) required to move between states.

Note that for each agent in Figure48, is listed a “weighting” of indicator values which defines their preferences over nodes. So, the company gives the “profit” indicator a weighting of 1, but the “env” (environmental concern) indicator only 0.5. This is just a short-hand way of capturing the notion that this particular company prefers profits over environmental concern but that such issues are not ignored and if significant could override profit. Obviously, the meaning of such weightings is only discernable when considered against the values placed on indicators in nodes of the agent viewpoint digraph. Costs and additional explanatory comments can be attached to actions and nodes but these are not shown in the figure.

These static structures are not hard-coded into the Neg-o-Net code but stored in a text file (in the form of a kind of high-level language) the text file input into Neg-o-Net that creates agents with the specified viewpoints. Figure 49 shows a fragment of the input file (the full input file is given in appendix 1 below).

Figure 49. Example fragment of input text file to neg-o-net.

14.2.4 Temporal Structure

In the current version dynamic change occurs in the believed current world states of each agent and during negotiation when agreements and offers are made and stored. In the context of Figure 48, this means that as the model is executed the believed world states (current node) for each agent changes over time. This change occurs based on agents attempting to move to “better” nodes – as defined by the weightings placed on the indicator values.

The process of attempting to move to “better” nodes often requires agents to look for other agents to perform required actions (if they do not have the ability to perform the action required themselves). For this “action haggling” to occur agents enter into a negotiation process. In the current version only one semi-plausible negotiation protocol is implemented. The model also implements (for comparison purposes) agents acting independently in addition to (again for comparisons purposes) agents acting in perfect unison, exploring all possible mutual action sets and maximising their joint preferences (which may or may not be meaningful depending on the scenario). Consequently there are three distinct ways that the current mode can interpret the viewpoint input file and produce output.

When agents negotiate they use two kinds of communication – broadcast (messages sent to all) and one-to-one (one agent sends another a message – no others can read the message). During a dialogue agents track and store any agreements made with other agents (concerning actions to perform). These agreements are then executed when no more negotiation is possible.

14.2.5 Important Parameters

As stated above, all the major parameters are stored in the viewpoint input file (see Figure 49). This includes, the number of agents, the viewpoints of each agent, the action repertoires at each believed world state, the indicator values and weightings and possibly action costs. Collectively this information defines the agent side (subjective side) of a “scenario”. The other important aspect of the scenario is the incorporation of an environmental simulation (produced elsewhere).

14.2.6 Initialisation

As stated above, the model is initialised via the viewpoint file (see Figure 49). Currently the negotiation protocols are hardwired but in future implementations these could possibly be placed into the file too.

14.2.7 Key Algorithms

The currently implemented negotiation protocol follows a process of repeated dyadic agreements concerning actions to perform. Essentially, agents broadcast to all other agents a list of requirements (actions that they want to be performed but which they themselves can not perform alone) and a list of possible offers (actions they are able to perform). The offers are broadcast one-by-one throughout the negotiation rather than in one block at the start. The idea here is that agents are happy for others to know what they want, but would rather not let all agents know what they could supply until this is required to make a deal. This way, the least costly actions can be offered first.

If an agent sees an offer that satisfies one of its requirements then it directly communicates with the offering agent. If the offering agent still has outstanding requirements it will ask for a deal based on this. If an agreement is made between two agents to perform certain actions, this is broadcast to all other agents. In this way all deals are transparent (there are no secret deals). Agreements, once made, are always honoured. Agents stop negotiating when they can no longer satisfy any more requirements. When all agents have stopped, agreed actions are performed.

Essentially then, agents simply form paired (dyadic) agreements to perform actions that are mutually beneficial. Agents only agree to perform actions that they believe will take them to a better node (based on their viewpoints, the actions they have decided to take and any announced agreements).

Note, as stated previously, this negotiation protocol was implemented purely as a “first example” of the kinds of possible protocols (or strategies) that could be implemented based on feedback from regional application partners.

14.2.8 Description of Model Dynamics

The dialogue consists of requests, offers and acceptances of action by the various parties. The dialogue represents a collective progressive exploration of the parties’ belief nets for possible ways to improve their indicators (which represent their goals). Each time a particular possible pathway is blocked others are tried. The process stops whenever a set of actions is agreed. These actions then change the situation and the negotiation may begin again.

14.2.9 Implementation details necessary to get the simulation to run but not considered important for the results

There is little that is ‘extra’ in this model, since it is fairly simple. However it is likely that the exact order and extent in which agents consider their own belief nets will not always be significant to the results, but this needs to be confirmed with respect to the chosen object domains.

14.2.10 Implementation Language

The model is implemented in Sun Java2 JDK1.3.1. All necessary libraries are packaged into the JAR file. Additionally the model has been implemented in SDML. This “duel” implementation approach allows for flexible experimentation and exploratory investigation (SDML) and rapid execution, cross-platform compatibility and easy interfacing with other (e.g. environmental) models (Java).

14.2.11 Source Code

The executable JAR that also includes the source codes (plus rudimentary documentation) is available at http://www.davidhales.com/firma/negonet.

14.3 Conclusions

14.3.1 Example Simulation Output

Figure 50-Figure 52 below show some of the actual output produced during a negotiation process based on the viewpoints shown in Figure 48. Iterations are produced of perception (agents locate their current node), negotiation (make offers, post

Figure 50. Example output from Neg-o-net model (I)

Figure 51. Example output from Neg-o-net model (Ii)

Figure 52. Example output from Neg-o-net model (Iii)

requirements and form agreements) and actions (agents perform agreed actions). Note, for the given viewpoints and implemented negotiation protocol, this output is not meant to represent any actual real negotiation process but is given as an example of the kind of process that can be captured by the model.

14.3.2 Results claimed as significant

The significant result obtained from Neg-o-Net version 1, is illustrated by the textual negotiation trace (see Figure 50 to Figure 52) and its relationship with the viewpoint representation. From a fairly loose and intuitive viewpoint representation (see Figure 48) multiple agents can negotiate at the level of actions in a way that is understandable to those with knowledge of the domain. As stated previously, the model is a point of departure for producing more specialised and realistic neg-o-net versions that suit different regional applications.

14.3.3 Methodological Lessons

This initial version of neg-o-net was produced to solidify discussions concerning the possibility of a generic negotiation framework from which regional applications could be derived. In this sense it is part of the first iteration, whereby the model is presented to the regional groups with domain expertise for their area and then modifications are made. At this stage, this method of development appears to be productive. However, in order to produce suitably specialised models, several iterations will be required requiring close liaison with the regional partners.

14.3.4 Future Development

As stated in previous sections the next version of the model is being developed for the Maastricht regional application. This will involve a “government agent” which produces plans, and a set of stakeholder agents that comment on those plans. The government agent modifies the plans based on the stakeholder response – effectively incorporating stakeholder beliefs into its own viewpoint. Here then, a kind of “second order” knowledge will be stored by the government agent – knowledge about others beliefs. The negotiation process will involve iterations of government plans and stakeholder objections or suggestions, terminated when no further change is possible or when some maximum number of iterations has been executed. Additionally, viewpoints will be broken-up into a number of independent and concurrent digraphs that relate to specific issues (e.g. risk of flooding, cost to consumer, environmental impact etc.). It has been evident that a single digraph is not a sufficiently compact representation when there are several issues that need to be considered simultaneously. The graphs become horrendously large due to the combinatorial explosion for considering each possible world state and action.

14.3.5 Published works relevant to the model

For a rough lineage leading to Neg-o-Net version 1 see Dep-Net (Conte & Sichman 1995) then Part-Net (Conte & Pedone 1998). However, these models have different aims. For a previous negotiation model applied to the same context but with a different approach see Moss (2002).

Conte, R. & Sichman, J. (1995), DEPNET: How to benefit from social dependence, Journal of Mathematical Sociology, 1995, 20(2-3), 161-177.

Conte, R. and Pedone R. (1998), Finding the best partner: The PART-NET system, MultiAgent Systems and Agent-Based Simulation, Proceedings of MABS98, Gilbert N., Sichman J.S. and Conte R. editors, LNAI1534, Springer Verlag, pages 156-168.

Moss, S. (2002), Challenges in agent based social simulation of multilateral negotiation, Socially Intelligent Agents: Creating Relationships with Computers and Robots, Kluwer, pages 251-258.

Gilbert et al (2001), Computer Simulation and Participatory Research, Talk Presented at the SIMSOC-V workshop, September 2001, available at: http://www.soc.surrey.ac.uk/simsoc5/talks-page/talk05.htm.

Pedone et al (2000), Social & Institutional Influence - Why people accept policies. Available at: http://firma.cfpm.org/partners/internal-reports.html

14.4 Appendix 1

The full listing (actual input file to neg-o-net) capturing the example shown in figure 1 of which Figure 53 shows the first few lines.

Figure 53. Example Neg-o-net output

14.5 Appendix 2. Neg-o-net Version 2

After discussions with the Maastricht group concerning their case study, it was decided to add a new negotiation protocol to negonet. This would more closely reflect the actual process studied by the group. A form of “Policy agent mediated” negotiation was implemented in which stakeholder agents make proposals to a Policy agent. The agent assesses these and proposes plans back.

The Policy agent has preference weights over the other agents. It proposes plans to the agents to maximize preferences. Agents respond indicating their own satisfaction levels based on their preferences and any actions that they can perform. The Policy agent then extends / updates its viewpoint to include these – i.e. it learns. So the Policy agent can start with an empty viewpoint and induce one from dialogues with agents. Figure 1 shows a schematic of the communication structure in Negonet version 1 and Figure 2 shows the contrasting structure for Negonet version 2. Figure 3 shows example output from the first iteration of negotiation with Negonet version 2 with the same input script as given previously.

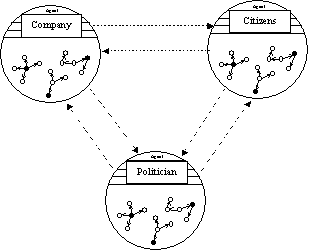
Figure 54. Negonet version 1, negotiation structure

Figure 55. Negonet version 2, negotiation structure

Figure 56. Example output from negonet version 2

15 The PANDORA Model

R. Conte, R.Pedone, ISTC-CNR (IP-CNR)

15.1 Relation of this model to the FIRMA aims

The ISTC group aimed to provide (a) an ontology (norms, negotiation, etc.), (b) a taxonomy (institution, side-institution, etc.), and (c) abstract multi-agent models, which are essential conditions for the achievement of the FIRMA last three aims, with special reference to

· the negotiated design of policies, and

· the diffusion of such innovation (“innofusion”), by means of agent-based simulation.

In this sense, it provides a baseline that can be instantiated to specific environmental and social problems and policies, and to a variety of social and institutional scenarios.

15.2 Introduction

The PArt-Net Dynamics Of Regulation among limited autonomous Agents (PANDORA) is an extension of PART-NET, an agent-based computational model developed for the formal investigation of partnerships formation, to modelling norm-based dynamics among autonomous social agents, consisting of two main sub-processes: the negotiation-based issuing of new policies, and their adoption and execution on the part of autonomous social agents.

The current extension of the model is intended to formally describe the social and cognitive processes and mechanisms characterising the dynamics of norm issuing, adoption and dissemination among intelligent interacting agents at different levels of complexity, i.e., macro-agents and micro-agents. The former (institutions and organisations) are involved in the negotiation process for the issuing of new norms, which influence individual agents through their mental states. At the current stage, the model is designed at the abstract level. No direct application to real case study has been made. The Part-Net Negotiation Model was developed by ISTC-CNR (IP-CNR).

15.3 Modelling Context

15.3.1 Description Domain Context

The model is a general framework for formalising and possibly simulating the introduction of new policies and their dissemination in a population of autonomous agents. Each agent represents an autonomous, heterogeneous and versatile entity: it is endowed with cognitive machinery for the regulation of its behaviour. In a social environment (shared at least by two agents), a number of different and important issues are addressed by means of agent interactions, namely communication, adoption and negotiation.

15.3.1.1 Communication

Interaction among agents is often realised by means of communication. A simple form of communication is emission of simple signals with fixed interpretations. A more complex form of communication is the ‘message passing’ performed at least at two levels: one corresponding to the informational content of the message and the other corresponding to the intention of the communicated message. When the interaction among agents is performed by means of message passing, each agent ‘must be able’ to infer the intention of the sender regarding the sent message (e.g. KQML; KIF).

15.3.1.2 Adoption

By definition, agents are autonomous, but not self-sufficient. The PART-NET model enabled the description of interdependencies among agents and the formation of partnerships based upon them. However, the process leading agents to decide whether to accept and adopt others’ requests, in order to have one’s own accepted and adopted in return, was not addressed. The PANDORA extension is intended to describe the general ingredients and mechanisms of goal-adoption, as a fundamental process expanding agents’ activity. Furthermore, such expansion is crucial for describing regulatory interactions among agents, allowing for the model to be applied to the context of policy-making and evaluation.

Adoption implies considering the requests of other agents in the same environment when planning and executing one’s own actions, whether such requests are made by macro- or micro-agents. This involved two decisions that are taken by the recipient: to recognise something (a message) as a request, and to adopt it, i.e. to transform it into one’s goal, and possibly satisfy it. The first decision, which is called acceptance, is probably more intuitive in the context of normative requests: agents must recognise an object (a message) as a normative request in order to adopt it.

15.3.1.3 Negotiation

In our view, negotiation is a process of bilateral adoption: agents negotiate when each wants the other to adopt all or part of its goal(s). The process of negotiation implies that one or more of the agents involved makes a given request (candidating a norm). This is either agreed upon by the counterpart and finalised as such, or is modified through a recursive process of feedback and re-candidacy among the partners until either agreement is reached or negotiation fails. The goal(s) finally adopted may be more or less far from the initial candidates, and the level of respective satisfaction varies as a function of this.

The social entities considered are at different levels of complexity: macro-agents include institutions and organisations (e.g. private companies), micro-agents are individual citizens. But the typology may also include meso-formations, federation community, groups creation associated with a single “facilitator” to which agents surrender a degree of autonomy (NGO, unions, parties, etc.).

15.3.2 Original Purpose of Model

The PART-NET model aimed to

· describe the dependence relationships among agents

· autonomous

· heterogeneous agents

· different social level (Institutions / Citizens)

· endowed with different actions, goals, beliefs and obligations and strategies

· calculate the formation of partnerships among them.

The PANDORA model is instead aimed to provide a theory-driven instrument for the description and simulation of regulatory interactions, and more specifically, to

· Describe the negotiation process among different entities (e.g., institutions and organisations) leading to a given measure of policy to be issued.

· Predict its impact under different mechanisms of norm adoption, i.e.:

· incentive-based or sanction-based

· social control-based (intra-group sanctions via reputation)

· social learning-based (what is now called “biased” transmission (Heinrich, 2000), i.e. selective monitoring and imitation.

The rationale of this model draws upon current studies of cultural transmission and diffusion of innovation (Heinrich and Boyd, 2000; Heinrich, 2000; Bowles, 1998). According to these studies, the typical pattern of results found in empirical studies of the dissemination of innovations is better reproduced by simulations of “biased” transmission models, where agents apply social and cognitive strategies as exemplified above, than by “environmental learning” models. By “environmental learning” we mean the import and reproduction of innovations which are expected to maximize the performer’s fitness or utility. To ensure that the model has a capability of predicting the impact of policies, sufficiently realistic strategies of dissemination need to be implemented.

15.3.3 How was the Model Actually Used

PART-NET and the main components of the PANDORA extension have been adopted for the initial design of the Neg-o-Net model developed by the Centre for Policy Modelling at Manchester Metropolitan University, in collaboration with our group.

15.3.4 Relationship to other Models

PANDORA represents a natural extension of the Part-Net model (Conte & Pedone, 1998) which, in turn, is a derivation of the DEP-NET model (Conte & Sichman, 1995). DEP-NET and PART-NET were produced by the ISTC-CNR (once, IP-CNR) group and the SimCog group of S. Paulo, Brazil. At the current stage of its development, PANDORA has inspired the development of the Neg-o-Net model by the CPM-MMU group.

15.4 Model Design

15.4.1 Intended interpretation

Both PART-NET and PANDORA are to be interpreted as theory-driven formal-computational tools for the description of interactions among limited autonomous agents in a common environment. The models are currently specified at a rather abstract level, in order to be implemented in a wide range of situations and for a variety of applications.

The target phenomenon is innovation in policy-making, and more specifically, the dynamic, participatory or negotiation-based issuing of designed policies, their impact on autonomous agents, and their dissemination.

Each agent is defined by a set of beliefs, goals, actions and strategies that represents the stakeholder viewpoint and intention. Both the negotiation and the adoption process are designed in terms of a general mechanism for generating new mental states (namely, beliefs and goals), starting from the interaction among current inputs and existing ones. Norms (or policies) are treated as “artefacts” produced by negotiating social entities which are processed and possibly adopted by their addressees and get disseminated in the population as an effect of different strategies, drawing upon the “biased transmission” model.

15.4.2 Original Sources for Model Design

PANDORA is an agent-based computational model developed for the formal investigation of processes of negotiations involved in partnerships formation. As mentioned earlier the Part-Net Negotiation model represents an extension of the Part-Net model (Conte & Pedone, 1998) which is a derivation of the Dep-Net model (Conte & Sichman, 1995). Dep-Net and Part-Net were produced by ISTC-CNR (ex. IP-CNR) Rome modelling group and the SimCog group S. Paulo.

15.4.3 Static and Temporal (dynamic) Structures

PANDORA is an abstract model. Each agent represented in it is defined by a set of characteristic structures like beliefs, goals, actions, strategies, trust and reputation. These structures are static in the sense that they are both present in all the agents. Moreover, they are dynamic regarding the agent’s ability to change contents or values and generate or delete them.

Real static structures are the basic mechanisms of norm adoption and strategies of implementation (see Appendix).

15.4.4 Important Parameters

The important parameters of the model are: number of agents, and the agent’s characteristics: number/content/type/value of beliefs, goal, actions, strategies, etc.

15.4.5 Initialisation

A possible model implementation via simulation could be initialised to represent different social/cognitive scenarios.

15.4.6 Key Algorithms

An important algorithm is one that defines the norm negotiation process. Negotiation is defined as a bilateral norms adoption: agents negotiate when each wants the other to adopt all or part of its goal(s). The process of negotiation implies, as an example, that one of the agents makes a given request of another agent. In principle, this is either agreed upon by the counterpart and finalised as such, or is modified through a recursive process of feedback and re-candidacy among the partners until either agreement is reached or negotiation fails. At the current stage the negotiation algorithm is under development.

15.4.7 Description of Model Dynamics

In addition to the dynamics characterizing PART-NET, the PANDORA model dynamics will be strictly related to a working definition of the negotiation algorithm described above.

15.4.8 Implementation Language

The model is not currently implemented. The implementation language could be any programming languages such as C or Java.

15.4.9 Source Code

The source code is a pseudo-code very close to an object programming language.

15.5 Conclusions

15.5.1 Results claimed as significant (and Methodological Lessons)

These include

· a preliminary ontology of social entities and objects involved in policy innovation:

· Institution, an agent endowed with goals, beliefs and actions characterised by

· tutorial goals over a given population, where a tutorial goal is defined as the goal to influence another agent or set of agents to acknowledge and promote their interest (and interest being what increases the achievement of one’s goals)

· adoption and negotiation mechanisms

· the “capacity” (action) to candidate policies, or norms, where a norm is an external “artefact” in the form of a prescription (an obligation to accomplish an action on a set of agents) that, to take effect, must be adopted by the addressees.

· Sub-institution, hierarchically subordinate, which receives input from the previous one, and participates in the negotiation process, by providing feedback on candidate norms.

· Side-institutions, non-subordinate, characterised by tutorial goals of control over innovation against some specified finality (e.g., sustainable development)

· Endowed with the same properties as above

· participating in the negotiation process.

· Extension of the general theory of adoption to modelling negotiation

· Integration of the “biased transmission” model in an agent-based framework.

· A model for describing adoption, dissemination and innovation of norms.

15.5.2 Future Development

These include

· The construction of an algorithm for the implementation of PANDORA and for running simulations of both real situations and for obtaining experimental results about

· The impact of specified policies

· The respective effects of strategies of adoption

· The interplay between negotiation and impact

· The effect of different strategies of adoption on dissemination.

· The validation of the adoption and negotiation model

Refinement of the current ontology.

15.5.3 Published works relevant to the model

Bowles, S.1998 Cultural Group Selection and Human Social Structure: The effects of segmentation, egalitarianism, and conformism. Electronic document. http://www-unix.oit.umass.edu/~bowles/papers/cultural.PDF

Conte et al (2000), Social & Institutional Influence - Why people accept policies. Available at: http://firma.cfpm.org/partners/internal-reports.html

Conte, R. & Sichman, J. (1995), DEPNET: How to benefit from social dependence, Journal of Mathematical Sociology, 1995, 20(2-3), 161-177.

Conte, R. and Pedone R. (1998), Finding the best partner: The PART-NET system, MultiAgent Systems and Agent-Based Simulation, Proceedings of MABS98, Gilbert N., Sichman J.S. and Conte R. editors, LNAI1534, Springer Verlag, pages 156-168.

Heibrich, J. (2000) Cultural Transmission and the Diffusion of Innovation, http://webuser.bus.umich.edu/henrich/diff2.pdf

Heinrich, J, and Boyd, R. (2000) The Evolution of Conformist Transmission and the Emergence of between-group differences, Evolution of Human Behaviour, 19: 215-242.

Pedone, R. & Conte, R. (2000) The Simmel Effect: Imitation and Avoidance in Social Hierarchies. In S. Moss & P. Davidsson (Eds). Multi-agent based simulation, Springer, 2000.

Pedone, R., Conte, R., (2001) Dynamics of Status Symbols and Social Complexity, Social Science Computer Review, Vol. 19, No. 3, Fall 2001, 249-262.

Pedone, R., Parisi, D., (1997), In what kinds of social groups can “altruistic” behaviors evolve?, Simulating Social Phenomena, R. Conte, R. Hegselmann, and P. Terna (Eds), Lecture Notes in Economics and Mathematical Sistems 456. Springer-Verlag Berlin Heidelberg. 1997.

15.6 APPENDIX

15.6.1 (some) Basic structures of the PANDORA model

AGENT STRUCTURE
Agent	# [numeric id]	[number]
Life	ALIVE/DEAD	[boolean]
Type	INSTITUTION / CITIZEN [GO, NGO, etc.]	[string]
Name	Agent Name	[string]

SECTION DEPENDENCE/KNOWLEDGE NETWORK
Net(n).	Network size	number
With (agent) “X”	Agent ID	number
Type	UNI / BI-LATERAL	boolean
Link	ACTIVE / NOTACTIVE	boolean

SECTION REPUTATION
reputation.public	# [numeric value]	number
reputation.self	# [numeric value]	number

SECTION TRUST
trust.public	# [numeric value]	number
trust.self	# [numeric value]	number

SECTION GOALS
goal	# [numeric ID]	number
content	Goal content description	string
name	Goal name	string
active	YES/NO	boolean
public	YES/NO	boolean
state	SATISFIED / UNSATISFIED	boolean
source	BUILTIN-INNATED / GENERATED ADOPTED / PLANNED / OBLIGATORY	string
value	Goal value	number
priority	LOW/MEDIUM/HIGH	string
SUB SECTION	GOAL DEPENDANCIES
dep_on_Ag	Dep. on Ag # [numeric id]	number
obj_id	Dep of obj # [numeric id]	number
obj_class	[redundant] GOAL, ACTION, BELIEF, ETC.	obj

SECTION ACTIONS
action	# [numeric ID]	number
content	body of action / content description	string
effect	instored state of the world: OBLIGATORY/NOT_OBLIGATORY	string
name	Action Name	string
public	YES/NO	boolean
availability	REUSABLE/NOTREUSABLE	boolean
source	BUILTIN-INNATED / GENERATED ADOPTED / PLANNED / OBLIGATORY	string
state	PERFORMED/NOTPERFORMED	boolean
cost	Action cost/value	number
priority	LOW/MEDIUM/HIGH	string
SUB SECTION	ACTION DEPENDANCIES
dep_on_Ag	Dep. on Ag # [numeric id]	number
obj_id	Dep of obj # [numeric id]	number
obj_class	[redundant] GOAL, ACTION, BELIEF, ETC.	string

SECTION BELIEFS
belief	# [numeric ID]	number
content	body of belief / content description	string
name	Belief Name	string
public	YES/NO	boolean
source	BUILTIN-INNATED/ACQUIRED (Individually or Socially)	string
truthness	# [numeric value]	value
SUB SECTION	BELIEFS DEPENDANCIES
dep_on_Ag	Dep. on Ag # [numeric id]	number
obj_id	Dep of obj # [numeric id]	number
obj_class	[redundant] GOAL, ACTION, BELIEF, ETC.	obj

SECTION STRATEGIES
strategy	# [numeric ID]	number
type	INCENTIVE BASED / SOCIAL CONTROL BASED / INST_REPUTATION BASED	string
name	Strategy Name	string
public	YES/NO	boolean
SUB SECTION	IF_CONDITION_STRAT
str_ifcondition(n).obj_id	apply condition: cond1, cond2, …	#[numeric id]
str_ifcondition(n).obj_class	apply to obj type: GOALS, ACTIONS, BELIEFS,	string
SUB SECTION	IF_CONNECTIVES_STRAT
str_ifconnective(cond1, cond2,...,condn, logial_operator)	condition connections: AND, OR, NOT
SUB SECTION	THEN_STRAT
str_then(object, function,[argument(...)])	object id; funtion(arguments) object=GOALS, ACTIONS, BELIEFS function=new_goal; new_action; new_belief; change_goal; delete_goal, etc.* A function can change/delete/generate new objects (i.e. Goals, Actions, Beliefs)

BASIC MECHANISMS OF NORM ADOPTION
INCENTIVE-BASED/SANCTION-BASED [top-down control]	agents adopt norms to obtain institutional incentives or avoid institutional sanctions.
SOCIAL CONTROL-BASED [bottom-up control]	A). agents control each other’s behavior w.r.t. norms accepted within the group. B) agents adopt norms to gain social approval, improve reputation, etc.
SOCIAL LEARNING-BASED [bottom-up control]	agents conform to the behavior of “significant” others (reputable, powerful, etc.)

---

[1] ‘Actors’ include individuals or units such as firms, pressure groups, or the local authority.

[2] It is important to state that this is not a deficiency of the models. They are specifically aimed, for good reason, at this level of negotiation.

[3] See Figure 1.

[4] See Appendix I

---

[GNG1]I don’t understand what this means.

[GNG2]This is only {0-10} in ZWG3